广义河床流体模型方程单调递减扭状孤波解的渐近稳定性

张 坤， 汪成伟， 张卫国

（上海理工大学 理学院，上海 200093）

1 问题的提出

广义河床流体模型方程

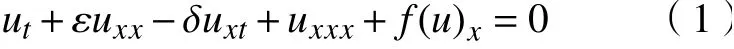
是一个重要的模型方程，其中，δ ≥0，f(u)=βup+1，p为任意的正整数，常数 β ＞0。 不难发现，当p=1时，式(1)即化为河床流体模型方程

方程(2) 源自于两相流体模型的研究[1-5]。当ε=δ=0，p=1时，方程(1)即化为KdV 方程[6]

当 δ =0，p=1时，方程(1)可以化为KdV-Burgers方程[7-12]

当 δ =0，p=2时，方程(1)可以化为MKdV-Burgers方程[13-16]

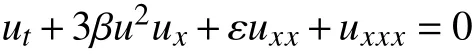
文献[3-5]用数值分析法研究了方程(2)在条件

下的周期初边值问题，文献[3-4]的研究证明，对周期初边值问题(2)和(3)采用通常的差分方法及Galerkin 有限元法得到的差分格式是不稳定的。为此，文献[4]利用特殊技巧给出了其在空间方向上的一个半离散稳定的差分格式。文献[5]用稳定化有限元法的思想，对问题(2)和(3)在一定条件下给出了一种全离散的稳定的差分格式，并用能量法证明了该差分格式的非线性稳定性及收敛性。

若 耗 散 系 数 ε,δ 满 足 ε+cδ ＜-λ0(ε+cδ ＞λ0)，则方程(2)有唯一的单调递减(递增)扭状孤波解；

若耗散系数 ε ,δ 满足- λ0＜ε+cδ＜0(0＜ε+cδ＜λ0)，则方程(2)有唯一的衰减振荡解。

文献[17] 求出了在耗散作用较小(即|ε+cδ|＜λ0)时，方程(2)衰减振荡解的近似解，且给出了近似解与真解的误差估计。但文献[17]并没有研究当 ε+cδ ＜-λ0时方程(2)单调递减扭状孤波解的稳定性。

受文献[17]的启发，本文将研究广义河床流体 模 型 方 程(1) 在 耗 散 系 数 ε,δ满 足ε+cδ ＜-λ∗(λ∗待求) 时，单调递减行波解u(ξ)的存在性，以及其是否具有渐近稳定性的问题。

2 方程(1) 单调递减扭状孤波解的存在性

运用平面动力系统的理论[19-21]来研究方程(1)在ε+cδ ＜-λ∗情况下单调递减行波解的存在性。

设方程(1) 具有行波解u(t,x)=u(ξ)=u(x-ct)，则u(ξ)满足

其中，c为波速。对上式关于 ξ积分一次，可得

这里的k是积分常数。由于本文主要研究的是系统的耗散效应，假设所研究的行波解满足

由此，在假设式 (4) 和 式 (5)条件下，方程(1) 的行波解满足

在接下来的讨论中，始终假设方程(1)的行波解满足式(4)和式(5)。

令x=u(ξ)，y=u′(ξ)，则方程(6)等价于如下平面动力系统:

由于方程(6)的有界解对应于系统(7)的有界轨线。 因此，可以通过研究系统(7)的有界轨线及其性态来研究方程(6)的解及性态。

命题1 当 ε+cδ ≠0时 ，系统(7) 在 (x,y)平面上不存在闭轨线和具有有限个奇点的奇异闭轨线。进而当 ε+cδ ≠0时，方程(1)不存在周期波解和钟状孤波解。

在平面 (x,y)上，系统(7)的有限远奇点的个数依赖于代数方程f(x)=βxp+1-cx=0 。 记x0=0，x1=(c/β)1/p，x2=-x1。 对于f(x)=0的实根，有以下结果：

a. 若c＞0， 当p为 偶数时，方程f(x)有3 个不同 的 实 根x0，x1，x2； 当p为 奇 数 时，方 程f(x)有2 个不同的实根x0，x1。

b. 若c＜0， 当p为 偶数时，方程f(x)仅有1 个实根x0； 当p为 奇数时，方程f(x)有2 个不同的实根x0，x1。

由于系统(7) 在c＜0且p为偶数时只有1 个奇点，故在 ε+cδ ≠0情况下方程(1)不存在有界行波解，所以，将不考虑这种情况。

因 此，J(xi,0)的 行 列 式 即 det(J(xi,0))等 于f′(xi)，i=0, 1, 2。 用 Δi表 示特征方 程在Pi(xi,0)处 的判别式，Δi=(ε+cδ)2-4f′(xi)，i=0, 1, 2。 从而可知Δ0=(ε+cδ)2+4c，Δ1=(ε+cδ)2-4pc； 如 果p为 偶 数，则有 Δ1=Δ2。

接下来运用平面动力系统的理论和方法[19-21]讨论系统(7) 奇点的类型，并给出在条件ε+cδ ＜0下的全局相图。

在条件ε +cδ ＜0 下 ，由于d et(J(0,0))=f′(0)=-c，易 知 当c＞0时 ，P0为 鞍 点；当c＜0且 Δ0＞0时，P0为 不稳定的结点；当c＜0且 Δ0＜0时 ，P0为不稳定的焦点。奇点Pi的类型如下所示：

a. 若c＞0， 当p为 偶数时，由于det(J(xi,0))=f′(xi)＞0 ， 当 Δ1＞0时 ，Pi(i=1,2)为 不 稳 定 的 结点；当 Δ1＜0时 ，Pi(i=1,2)为不稳定的焦点。当p为奇数时，由于 det(J(x1,0))=f′(x1)＞0， 当Δ1＞0时 ，P1为 不稳定的结点；当 Δ1＜0时 ，P1为不稳定的焦点。

b. 若c＜0， 当p为奇数时，系统(7)有2 个奇点P0(0,0)和P1(x1,0)。 又 因 为det(J(x1,0))=f′(x1)＜0， 故P1为鞍点。

用Poincare 变换对系统(7) 作无穷远奇点分析，易知在y轴的正负2 个方向上有一对无穷远奇点A1和A2。 其 中，A1位 于y轴 的 正 半 轴，A2位于y轴的负半轴。当p为偶数时，点Ai(i=1, 2)周围存在1 个双曲型区域；当p为奇数时，点Ai(i=1, 2)周围存在1 个抛物型区域。此外，Poincare 圆盘的圆周为轨线。

根据上述定性分析，可以得到系统(7) 在ε+cδ ＜0条件下的全局相图，如图1 所示。

由图1 可以得到命题2。

命题2 设 ε +cδ ＜0。 若c＞0，p为偶数，系统(7)存在2 个异宿轨线L(P1,P0)和L(P2,P0)(图1(a)和(b))；当p为 奇 数 时，无 论c＞0或c＜0，系统(7) 均 存 在1 个 异 宿 轨 线L(P1,P0)或L(P0,P1)(图1(c)～(f))。

由于平面动力系统中的同宿轨和闭轨对应于相应非线性发展方程的钟状孤波解和周期波解，异宿轨对应于扭状孤波解或振荡行波解等。因此，由命题2 和图1 可以得到定理1 和定理2。

定理1 设 ε+cδ ＜0， 若c＞0，p为偶数，方程(1)有2 个有界行波解(对应于图1(a)和(b)中的异宿轨线L(P1,P0)和L(P2,P0)) ；当p为奇数时，无论c＞0或c＜0，方程(1) 均有1 个有界行波解(对应于图1(c) ～ (f)中的异宿轨线)。

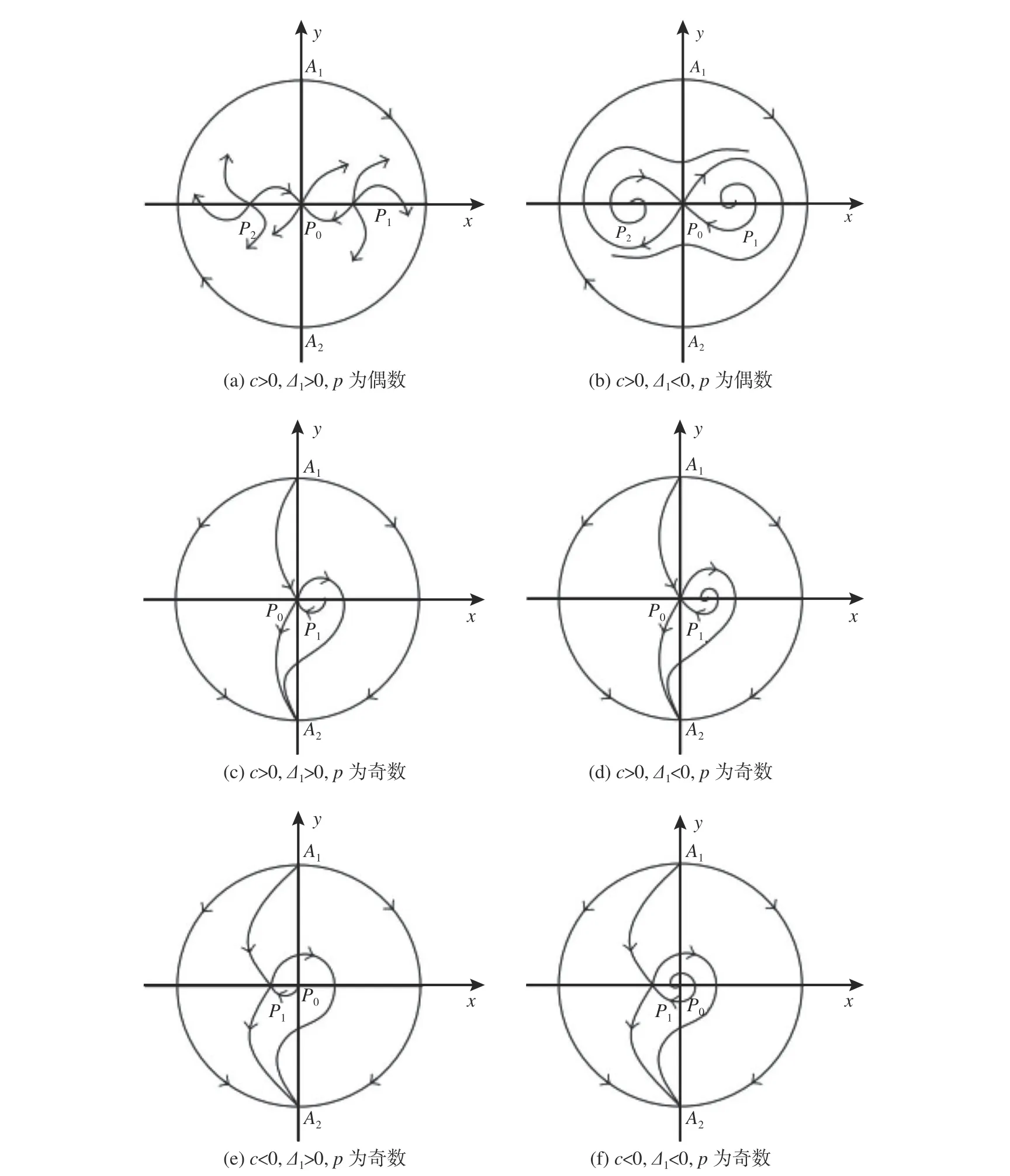
图1 ε +cδ<0时的全局相图Fig.1 Global phase diagrams when ε+cδ<0

现给出方程(1)的有界行波解受耗散作用影响的有关结论。

由于行波解u(ξ)在 沿x轴运动时其形状与波速保持不变，不失一般性，假设 ξ ˆ1=0 或ξ1=0，则定理2 的结论b 所描述的振荡行波解的性态如图2所示。

图2 c >0,-2 <ε+cδ<0时的振荡行波解示意图Fig.2 Schematic diagramsofoscillatory travelingwavesolutionswhen c＞0,-2 <ε+cδ<0

3 广义河床流体模型方程扭状孤波解的重要性质

故存在常数C，使得

现将式(24)两边同乘 e(ε+δc)ξ，有

4 单调递减扭状孤波解渐近稳定性定理

考虑方程(1)的初值问题，初值条件为

将式(31)对 ξ进行积分，并令积分常数为0，则有

定理4 的证明可分成扰动方程初值问题(32)和问题(34) 解的整体存在性和渐近稳定性两部分。先给出初值问题(32)和问题(34)解的整体存在性。

定理5 假设 Φ0∈H2， 则存在与u±无关的常数µ1,γ1(γ1≤γ0) 和 正 常 数C1， 使 得 当 |u--u+|≤µ1和N0=‖Φ0‖H2+‖Φ0ξ‖H1≤γ1，初 值 问 题(32) 和 问题(34)的解 Φ在X(0,∞)中是全局唯一存在的，且对任意的t∈[0,∞)满足

其中， Φξ由 式(31)定义， Φ0ξ为其初值。

为证明定理5，需要在局部解存在性的基础上给出一致先验估计。关于初值问题(32) 和问题(34)的解的局部存在性，有命题3。

命题3 (局部存在性) 假设N0≤γ0，则存在正常数T0(γ0)使 得问题(32) 和问题(34) 有唯一解Φ ∈X(0,T0)，且满足

命题3 可以利用Galerkin 方法或不动点定理按标准方法进行证明(可参考文献[25-26]等)。这里由于篇幅限制，省略证明过程。

在以下的推理过程中将用到2 个不等式，现以引理的形式给出。

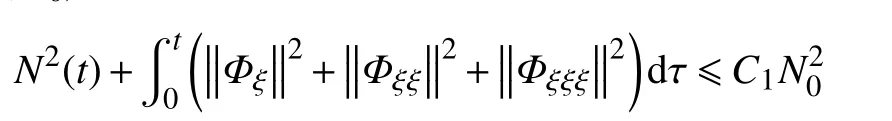
故式(37)可写为

综合不等式 (55)～(58)，对式(54)右端有下列估计：

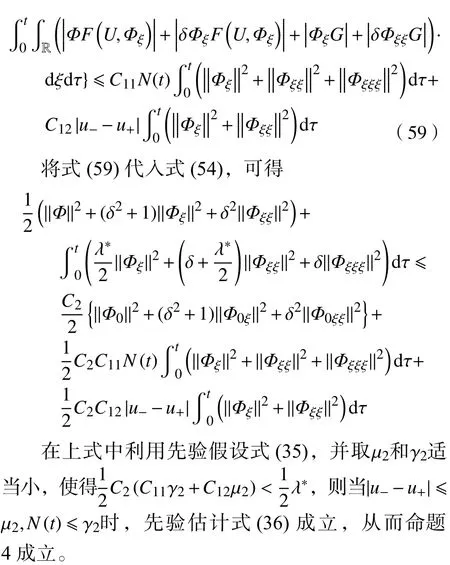
现在已经得到了初值问题(32) 和问题(34)的解的局部存在性和一致先验估计。在此基础上，通过连续性讨论来证明定理5。

现给出定理4 的证明。

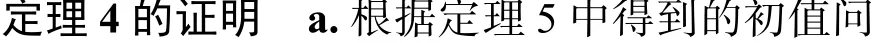
故定理4 得证。

通过以上对定理4 的证明，可得出广义河床流体模型方程(1)的单调递减扭状孤波解具有渐近稳定性。