基于自适应多尺度脑功能连接的局灶性癫痫发作检测方法研究

徐嘉阳 杨婷婷 李 雯 李 扩 杜昌旺 刘晓芳 盛多铮 闫相国 王 刚＃*

1（生物医学信息工程教育部重点实验室，西安交通大学生命科学与技术学院， 健康与康复科学研究所，西安 710049）

2（西安交通大学第一附属医院神经外科，西安 710061）

3（北京瑞尔唯康科技有限公司，北京 100071）

引言

癫痫是一种以突然、短暂、反复的癫痫性发作为特征的慢性神经系统疾病或综合征［1］。癫痫性发作则是大脑内神经细胞群阵发性异常超同步电活动的临床表现。反复、突然的癫痫性发作十分危险，不仅威胁到患者生命，还为其家庭增添了较大的负担。在临床上，医生通常利用长时程脑电图（electroencephalogram，EEG）来监测癫痫发作，然而由于这项工作乏味、耗时，并且很大程度上依赖于临床医生的自身经验和主观判断，导致人工检测结果的准确性和可重复性较低［2］。为了使得癫痫发作可以在较短的时间内被检测到，癫痫脑电自动检测和识别技术的发展尤为关键。

脑电信号具有非平稳性和非线性特征，因此脑电信号分析往往以传统的时域、频域或者时频结合的方法为主，通过计算各种非线性的特征值来区分脑电信号［3］。大多数的数据预处理方法是用小波变换对信号进行分解［4］，但是分层数、基函数的选择对结果产生很大影响，不具备对信号自适应的分解能力。本研究采用多元经验模态分解（ multivariateempiricalmodedecomposition，MEMD）［5］处理信号，此方法不需要根据先验知识选择基函数，能同时对多通道数据进行自适应分解，适合于分析具有高度相关性和非平稳性的脑电信号，可以增强定位脑电信号的频率信息的准确性，从而有效地提高对脑电信号的识别能力［6］。

目前所采用的癫痫检测方法多使用EEG 的幅值、主频率、变异系数、熵值等作为分类特征，然后利用支持向量机（support vector machine， SVM）［7］、决策树（decision tree， DT）、随机森林（random forest，RF）等方法进行脑电分类。但是，这些方法没有将大脑作为一个有机整体，没有考虑在产生行为变化或生理功能改变时大脑各部分之间会存在信息交换和流动。尽管这些方法在短时程脑电上检测结果表现优异，但在长时程脑电上检测结果的精确率指标偏低，不符合实际的临床需求。此外，在实际长程脑电的检测中，发作期的时间要远远短于非发作期的时间，数据集不平衡导致分类器决策边界偏移，最终影响到模型分类效果。因此，本研究采用有向传递函数（direct transfer function，DTF）计算不同脑区之间的流出信息，区分在癫痫发作时间段内和正常状态下不同脑区之间的信息流动的差异，并且采用代价敏感支持向量机（cost-sensitive support vector machine，CSVM）对提取的特征信息进行分类，利用不同类别的样本被误分类而产生不同的代价进行分类学习，从而解决数据不平衡带来的问题。

本研究利用多元经验模态分解将脑电信号分解出一系列本征模函数，利用其流出信息度作为特征，经过特征组合与降维后，通过CSVM 进行癫痫发作检测。结果表明，此方法具有较高的准确率、精确率、召回率及F2 值，达到了较好的癫痫发作检测效果。

1 材料和方法

1.1 实验对象

所用数据均源于西安交通大学第一附属医院，采用NIHON KOHDEN 公司的EEG-1100 脑电图机进行数据采集。该数据的采集使用19 导电极，电极位置按照国际10／20 标准，以头顶CZ 的电极为参考电极。数据的通带截止频率为0.5 ～60 Hz，采样频率为200 Hz。数据中关于癫痫发作点以及棘波波形的信息由交大一附院的两位具有临床经验的医生通过观察和评估被测患者的实际临床记录和表现进行标注。脑电数据的总时长为121.8 h，包含了44 次发作，其中癫痫发作期的平均时间98.7 s。

表1 给出了10 位患者的相关脑电数据信息。数据采集通过了西安交通大学机构评审委员会的批准，所有受试者都签署了脑电数据采集和后续脑电图记录分析的知情同意书。

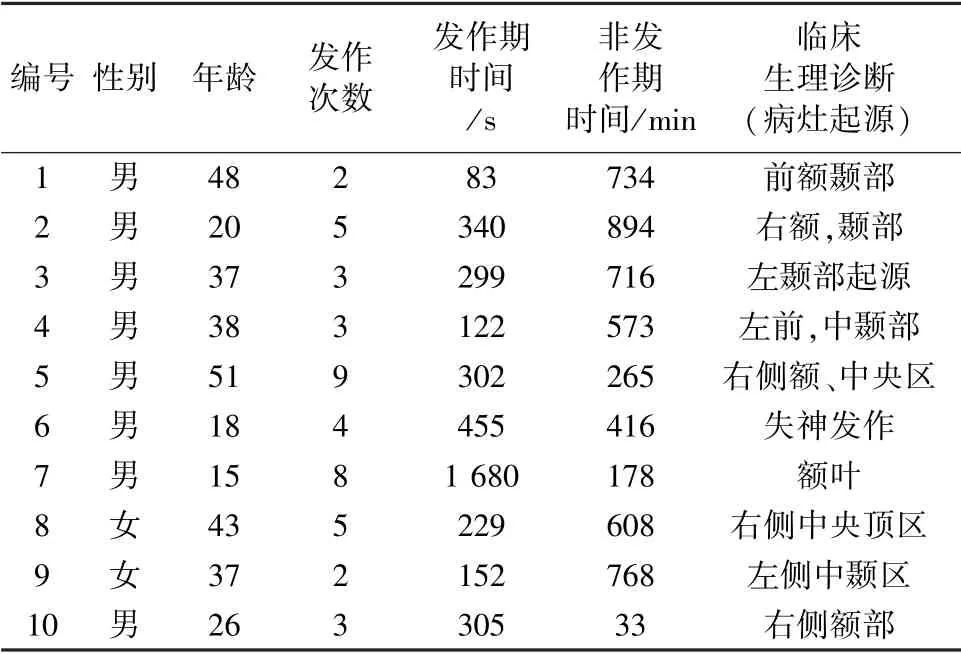
表1 患者信息表Tab.1 Patient Information

1.2 癫痫检测算法

为了在长时程脑电中识别发作期的脑电，本研究提出基于自适应多尺度脑功能连接的癫痫发作检测方法（adaptive and multiscale brain functional connectivity， AMBFC）。首先利用多元经验模态分解的方法，将19 个通道的脑电信号分解为7 个本征模函数（intrinsic mode function，IMF）分量和残量，接着再分别对7 个IMF 分量和残量及原始的脑电信号建立多变量自回归模型，用有向传递函数算法，提取不同IMF 分量的脑电信号和原信号在不同脑区的流出信息强度作为特征信息，并将此特征信息进行特征组合和PCA 降维，最后经过代价敏感支持向量机分类器，通过五重交叉验证得到检测结果。具体流程图如图1 所示。

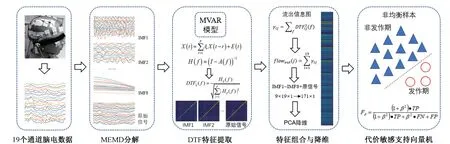
图1 所提出的癫痫检测算法（AMBFC）流程Fig.1 Flow chart of a novel epilepsy detection algorithm

1.2.1 多元经验模态分解

经验模态分解（empirical mode decomposition，EMD）是一种自适应信号时频分析方法［8］，可将信号分解成一系列IMF，其在处理脑电信号这一类非平稳非线性随机信号上具有明显的优势。然而，EMD 在处理多通道脑电图信号方面的应用仍然有限，故MEMD 作为传统经验模态分解的多元拓展引入癫痫发作检测这一领域。

首先采用滑动窗将脑电信号分割成短时信号。由于脑电信号在采集的过程中，经过了0.5 ～60 Hz滤波，因此，为了在后续分析的过程中能够分辨频率为0.5 Hz 的脑电信号，需要将脑电信号分割为时长至少为2 s 的片段。本研究选用2 s 的无重叠窗对脑电信号进行分割。

在t时刻，一个经过窗分割之后的N导联（N＝19）的脑电数据为

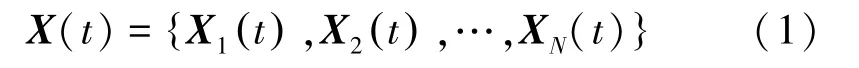
式中，Xn（t） 表示第n个通道的脑电信号。对此信号进行MEMD 分解，以下为具体步骤［5］：

步骤1：采用Hammersley［9］序列采样法，xθk＝［x1，k，x2，k，…，x19，k］表示在18 维球面上对应角θk＝｛θ1，k，θ2，k，…，θ19，k｝的方向向量集；

步骤2：计算原始脑电信号｛X(t)｝（1≤t≤T）在第k个方向向量xθk上的投影为｛pθk（t）｝（1≤t≤T），k为方向向量的总数；

步骤3：找到方向向量的投影信号｛pθk（t）｝（1≤k≤K） 极值对应的瞬时时刻｛ti，θk｝（1 ≤k≤K），i表示极值点位置，i∈［1，T］；

步骤4：用多元样条插值函数插值极值点［ti，θk，X（ti，θk）］共得到K个多元包络｛eθk（t）｝（1 ≤k≤K）

步骤5：对于球空间K个方向向量，局部均值可由下式计算：

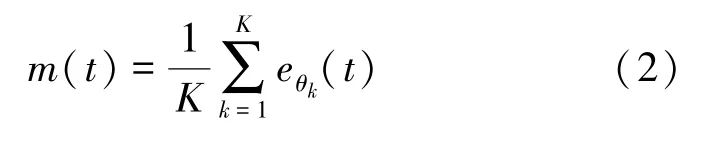
步骤6：通过d（t）＝v（t）- m（t） 提取固有模态函数d（t），如果d（t） 满足多元模态函数IMF 判断标准［10］，就将v（t）- m（t） 作为输入信号重新提取新的多元IMF 分量。由于不同信号分解出来的固有模态数目有差异，为了便于分类，需使得固有模态数目一致，故选用IMF 1～IMF 7。

经过多次MEMD 分解，原始的19 通道脑电信号｛X（t）＝｛X1（t），X2（t），…，X19（t）｝ 被分解为一系列IMF 分量和余量r(t) 的和，为

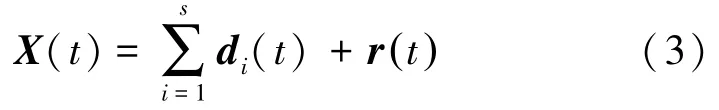
式中，s为IMF 的个数（s＝7），di（t）＝｛di，1（t），di，2（t），…，di，19（t）｝，r(t)＝｛r1（t），r2（t），…，r19（t）｝对应于19 通道脑电数据的19 组7 个IMF 分量和19 个余量。

定义Q(t) ＝｛q1(t) ，q2(t) ，…，q9(t) ｝， 其中qi（t），i ＝1，2，…，9 表示为

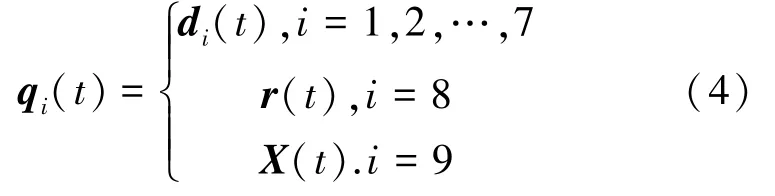
1.2.2 基于有向传递函数的特征提取

多通道脑电之间的相互关系可以用于评估脑区各部分的信息交流，而有向传递函数可以反映不同通道的脑电信号的相互关系［11］。为利用有向传递函数进行特征提取我们首先对每个qi（t）（i ＝1，2，…，9） 建立多变量自回归模型（MVAR），然后在求得MVAR 模型系数的基础之上，利用有向传递函数（DTF）提取不同脑区的流出信息强度，该特征能够反映不同脑电通道之间的流出信息。

在t 时刻，qi（t） 可以表示为

式中，N的取值为19。通过多通道自回归模型，该序列又可以表示为

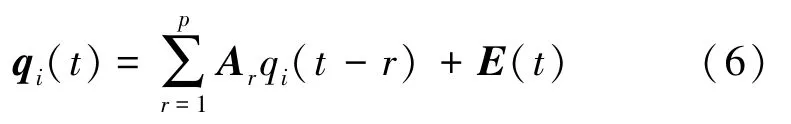
式中，p表示MVAR 模型的阶数，Ar为N×N的系数矩阵，r ＝1，2，…，p；E(t) 表示估计误差，理想情况下为均值为0 的非相关白噪声。

模型的阶数可以通过 Schwarz' s Bayesian Criterion （SBC）［12］来确定：系数矩阵Ar的估计可以用arfit［13］算法求得。然后对所获得的MVAR 模型求得的系数矩阵Ar作傅里叶变换，有

式中，f为离散频率变量。定义的传递矩阵为

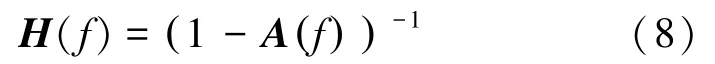
进而获得在频率f上从导联j到导联i的信息流：

式中，（f） 表示H(f) 的第i行第j列的元素，hi（f）表示矩阵H的第i列；DTFij（f） 表示在频率f时从导联j到导联i的信息流的强度和方向。

1.2.3 特征提取和降维

DTF 提取的特征为不同频率下各脑电极信号的信息流通情况，因此，对于每一个频率均提取19×19 的特征矩阵，在同一频段内，若有M 个频率数，则该特征矩阵的大小为19×19×M，这样的特征过于庞大，不利于分类器分类。因此，需要对特征进行降维和组合，具体的步骤如下：

步骤1：将所有频率下的特征值的平方进行累加，即

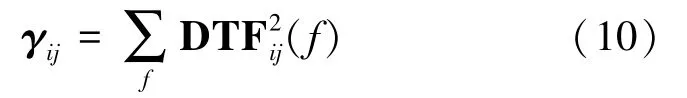
此时得到了某个频段内各个通道之间的信息流动的强度特征，这一步使得特征矩阵由19×19× M压缩到19×19。

步骤2：考虑到在癫痫发作期癫痫病灶区有高强度的放电，此区域的脑电信息流出强度会加大，故将特征值矩阵按列（或按行）累加就能得到每个通道的流出信息的强度，即

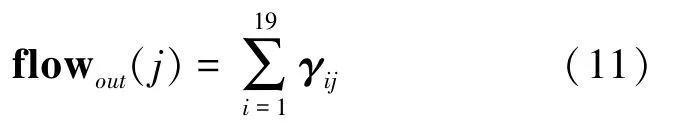
此时，特征矩阵由19×19 被压缩至19×1。将Q(t) 中每个qi（t） 得到的特征矩阵进行线性组合，得到171×1 的一维矩阵。

由于特征数目过多，选用主成分分析方法，对特征进行降维，利用线性矩阵变换，将高维空间的数据映射到低维空间。设样本为X ＝（x1，x2，…，xn），则算法的具体步骤为：

步骤2：计算样本的协方差矩阵：

步骤3： 利用奇异值分解（ singular value decomposition， SVD），求出协方差矩阵的特征值及对应的特征向量；

步骤4：对特征值从大到小排序，根据贡献度，选择最大的k个值，将其特征向量分别作为行向量组成特征矩阵P，其中，k值的大小由特征值数目的占比决定；

步骤5：将数据转换到k个特征向量构建的新空间中，即Y＝PX。

将经降维后的特征放入分类器进行学习，从而区分发作期的脑电信号和非发作期的脑电信号。

1.2.4 代价敏感支持向量机分类

由于在使用SVM 模型时，要求正反标记的样本量相差不大，然而在实际长程脑电中，癫痫发作期的时间远远短于非发作期，使得样本数目相差较大，从而造成SVM 模型倾向于数目较多的一类样本，进而影响分类模型的准确度。基于此，引入CSVM［14］，该方法在建模时将不同类别样本的误分类代价考虑在内，并将这些误分类代价嵌入到标准SVM 算法中。

CSVM 算法和SVM 算法的主要区别在目标函数上。其目标函数和约束条件为

目标函数：

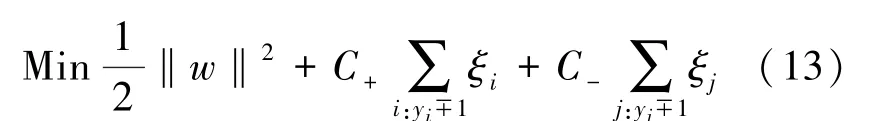
约束条件：

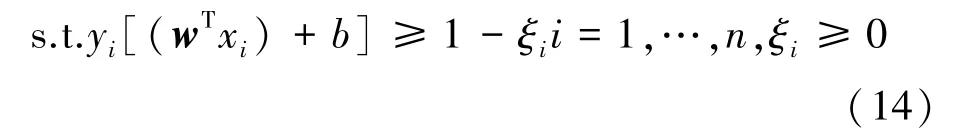
式中，C-＝C，C＋＝w1×C-，C是支持向量机SVM 的基惩罚因子，w1 是惩罚因子调整系数。

采用网格搜寻的方法［15］对算法中的参数C和w1 寻优，选用高斯径向核函数，惩罚系数C的取值范围为2-10～210，步长为0.5，w1 的取值范围为1 ～21，步长为0.5。通过C和w1 的不同取值，我们使用一个指标Fβ作为评估值，找出Fβ最高时对应的参数，此时即为相应的最优参数组合。Fβ表示为如下：

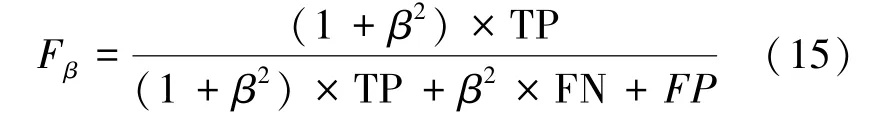
式中，真阳性（TP）表示算法和医生都判断为发作期的片段数；假阳性（FP）表示算法识别为癫痫发作期而医生标记为非发作期片段数；真阴性（TN）表示算法和医生都判断为非发作期片段数；假阴性（FN）表示算法识别为非发作期而医生标记为发作期片段数。此处，将β取为2（此权重使得FN 的意义大过FP），因此式（14）可以表示为

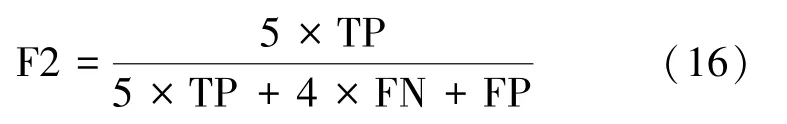
为了对结果进行更精准的评估，用于测试的数据必须与用于训练模型的数据区分开来。因此，我们采用双重交叉验证的方法，首先将每一个患者的脑电数据平均分为5 组，每次用4 组数据做训练，一组数据用来测试。为了在训练中建立最优的CSVM 分类器，对训练集进一步进行五折交叉验证。随机选择训练集的80%，建立CSVM 模型，并利用该模型在其余20%的训练集上的验证结果计算Fβ，以此来评估和选择最优模型。CSVM模型训练完成后，通过预留的测试集测试模型，评估该模型。将5 次的结果进行平均，作为最终测试结果。

1.2.5 算法评估标准

通过比较本文算法对癫痫发作期、非发作期的检测结果与医生所做标记的差别，将每个患者的五次交叉验证的平均结果作为依据，评估算法的性能。本文采用以下几项指标进行评估，这些指标定义如下［16-17］：

（1）准确率（Accuracy）

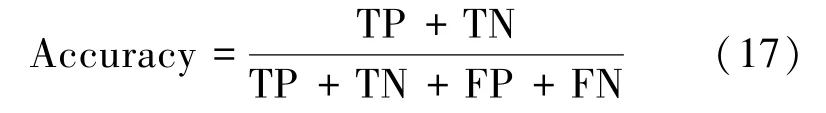
（2）精确率（Precision）

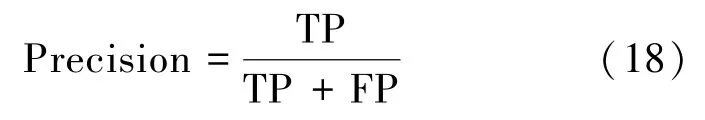
（3）召回率（Recall）

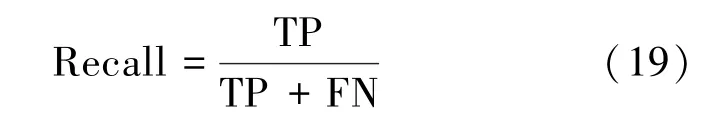
（4）F2 值

2 结果

2.1 AMBFC 算法的癫痫发作检测结果

经过2 s 时间窗分割，所获得的训练样本的平均非发作期片段数为12 439，平均发作片段数为157，测试样本的平均非发作期片段数为3 110，平均发作期片段数为39。经实验发现，如果降维时保留特征信息的数目为原特征数目的85%，可取得最优结果，因此在PCA 的过程中，将主成分占比设置为85%。

10 位患者癫痫发作检测的结果及平均值如表2 所示。通过五重交叉验证，得到10 位患者癫痫发作检测的准确率为98.60% ±2.49%，精确率为81.90%±16.67%，召回率为81.40%±14.16%，F2值为0.80±0.16。本方法的各项指标都在较高的水平。

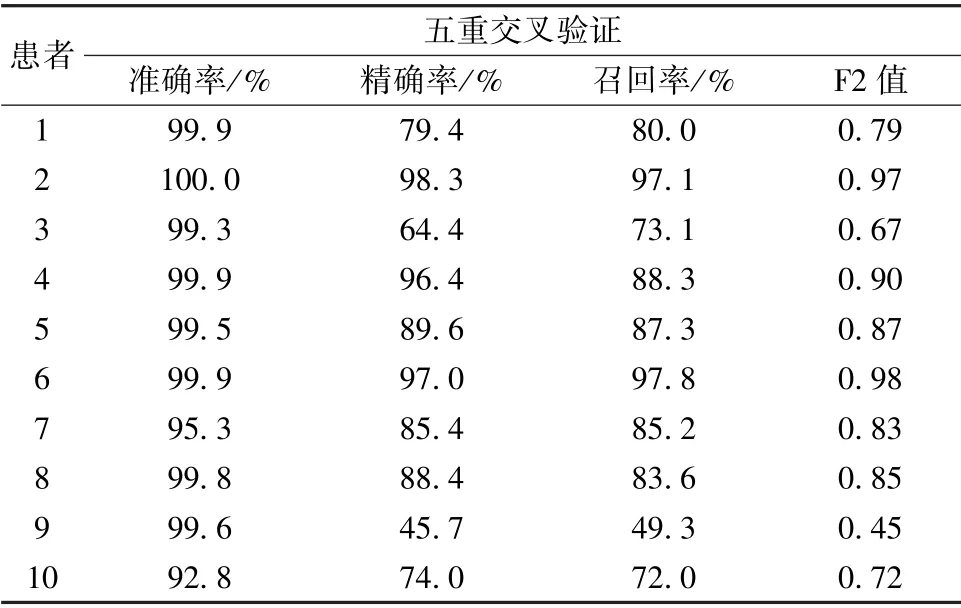
表2 不同癫痫患者使用AMBFC 方法的癫痫检测结果Tab.2 Epilepsy test results of different epilepsy patients using the proposed AMBFC method

2.2 基于DTF 不同本征模函数癫痫检测结果对比

为了讨论不同IMF 分量的脑电特征对检测结果的影响，利用IMF1 ～4 的特征分别进行CSVM 分类，并与AMBFC 算法得到的结果进行比较。首先利用MEMD 分解得到IMF1～4，然后采用DTF 算法求出IMF1～4 的信息流出特征，进行CSVM 分类，并与用AMBFC 进行分类的结果进行比较。仅针对患者1 进行研究，将各IMF 分量的癫痫发作检测结果与AMBFC 算法的检测结果进行比较。

基于准确率、精确率、召回率、F2 值等4 项指标的对比结果如图2 所示。由图可见，AMBFC 算法在保证高准确率的情况下，在精确率、召回率和F2 值等指标上也都达到了很高的水平，并且用AMBFC方法提取特征的各项指标均高于用各IMF 分量提取特征的指标，说明了AMBFC 算法对于这些癫痫患者的分类结果相比于用各IMF 分量作特征提取和分类更具有优势。由于各IMF 分量的信号可以为癫痫检测提供不同的有用信息，将这些信息聚集在一起可以为CSVM 分类提供更多癫痫发作信息交换特征，所以AMBFC 算法可以提升癫痫检测的准确率、精确率、召回率和F2 值。

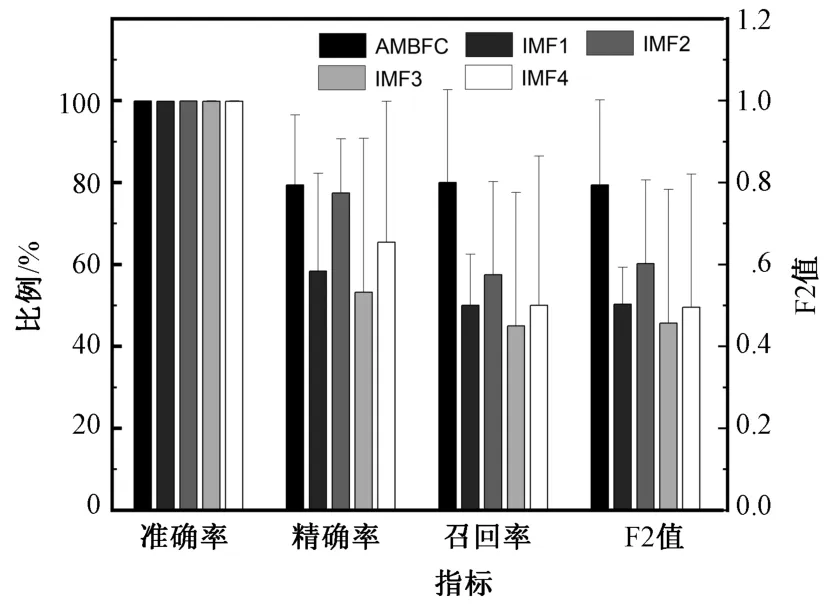
图2 用不同IMF 分量的特征进行癫痫发作检测结果对比图Fig.2 Comparison of results of epileptic seizure detection using features of different IMFs

利用患者1 的随机2 000 个非发作期样本和30个发作期样本，对不同IMF 分量的脑电信号进行信息流特征提取，并利用t-SNE 降维［21］可视化。蓝色的点表示非发作期样本，红色的点代表发作期样本。其中，图3 （a）为IMF1 分量的流出信息特征t-SNE 降维可视化的结果，图3 （b）为IMF2 分量的流出信息特征t-SNE 降维可视化的结果，图3 （c）为IMF3 分量的流出信息特征t-SNE 降维可视化的结果，图3 （d）为IMF4 分量的流出信息特征t-SNE 降维可视化的结果，图3 （e）为原信号和全部IMF 分量（即AMBFC 算法）的流出信息特征t-SNE 降维可视化的结果。

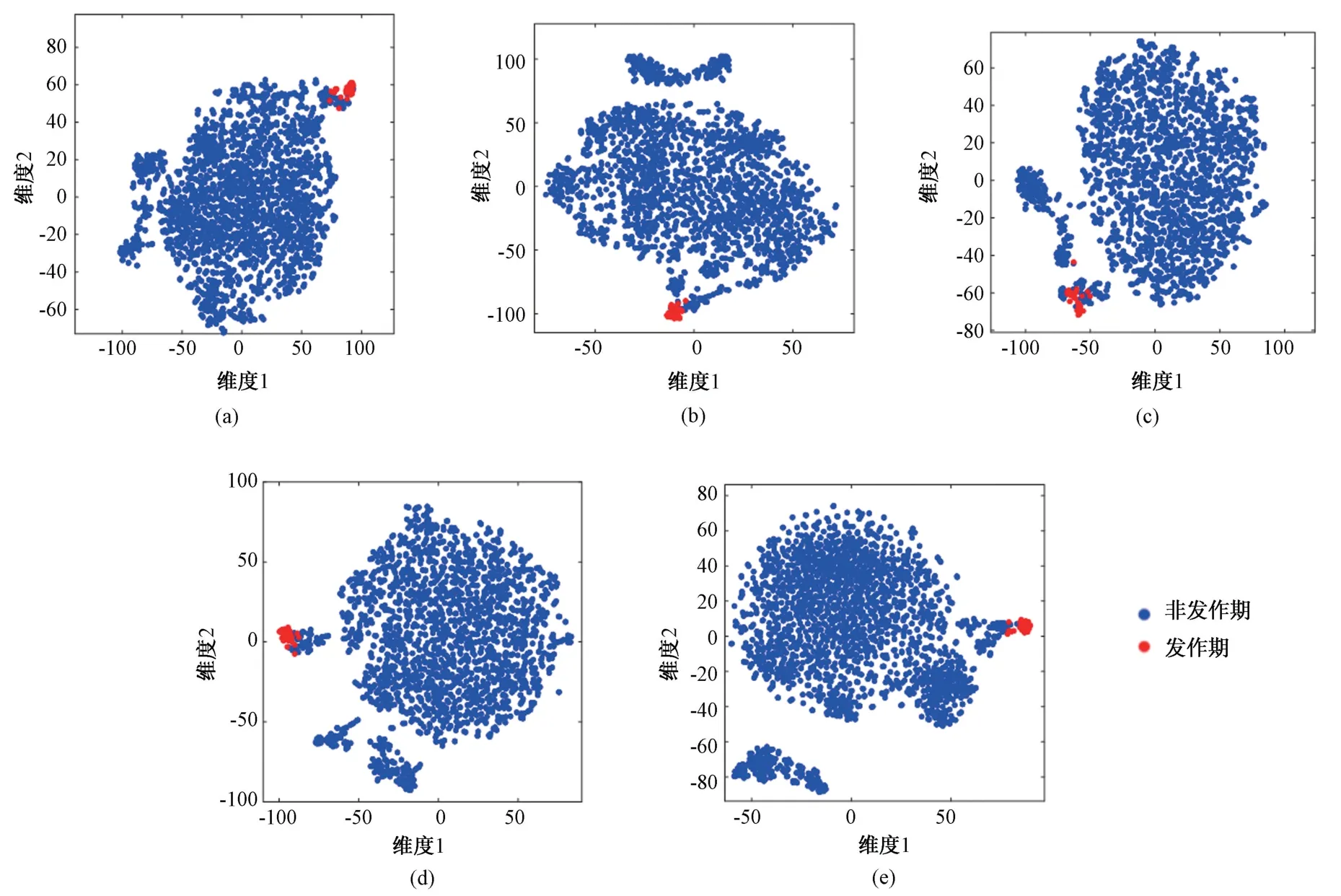
图3 不同IMF 分量特征经t-SNE 降维可视化结果。（a） IMF1；（b）IMF2；（c）IMF3；（d）IMF4；（e）AMBFC Fig.3 t-SNE dimension reduction visualization results of different IMF component characteristics. （a） IMF1；（b）IMF2；（c）IMF3；（d）IMF4；（e） AMBFC

可以看出，IMF1 ～4 分量的脑电信号提取出的特征经过降维可视化之后，发作期和非发作期的样本均有较高的重合性，视觉可分性不理想，而AMBFC 提取的特征视觉可分性要明显优于各IMF分量。这些可视化降维的结果与图2 中各项指标的分类结果一致。

2.3 基于不同算法的癫痫发作结果对比

为了更加客观地对AMBFC 方法的癫痫发作检测性能进行评价，选取DTF-CSVM 算法和近几年文献中报道的最新方法，用相同的数据集进行模型的训练和测试。其中，DTF-CSVM 算法相较于AMBFC算法，直接采用DTF 提取特征［18］，而未对脑电信号进行MEMD 分解，即仅对原信号建立MVAR 模型，提取各通道脑电数据的信息流特征，随后将特征进行组合和CSVM 分类。AMBFC、DTF-CSVM 方法及与最新论文［19-20］］对比的结果如表3 所示。由表可见，相较于DTF-CSVM 和EWT 算法，AMBFC 算法在各项指标上都取得了最优结果，而相比于Fusion 算法，在除召回率之外的其他指标上都取得了更优结果，由于癫痫发作期和非发作期的样本存在严重非均衡化的问题，需要同时评估其精确率和召回率，本研究将F2 值作为最主要的评判指标，基于此认为AMBFC 算法相较于Fusion 算法结果更优。

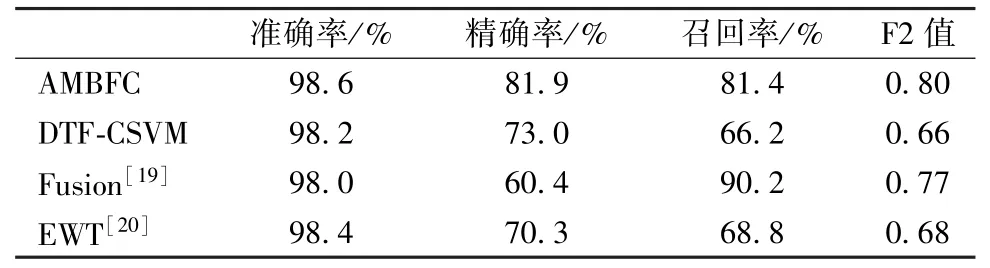
表3 使用不同方法的癫痫检测结果对比Tab.3 Comparison of epilepsy detection results employing different methods

3 讨论

目前，脑电在癫痫的临床诊断中已经有较为广泛的应用。本研究针对长时程脑电癫痫发作检测的问题，采用AMBFC 算法对采集的脑电信号进行癫痫发作检测。首先利用MEMD 算法对脑电进行自适应分解，再通过多变量自回归模型计算有向传递函数，建立多尺度的脑功能连接，从而提取不同脑区之间的信息流出强度，最后利用代价敏感支持向量机对发作期和非发作期的数据进行分类，在准确率、精确率、召回率和F2 值等4 项指标上取得了较优的结果，为长时程脑电中的癫痫检测提供可行方案。

由于采集到的脑电信号具有多通道、非线性、非平稳性的特点，采用MEMD 算法对多通道数据进行自适应分解。MEMD 是一种数据驱动的分解方法，可定位多变量、非平稳、低信噪比的脑电信号的时频信息，且具有较强的自适应性，有助于在多个尺度上发现内在模式，而不要求信号为谐波信号或平稳信号［22-23］。本研究通过比较ABMFC 和DTFCSVM 算法，证实了MEMD 算法可以增强定位脑电信号的频率信息的准确性，从而提高了对发作期和非发作期脑电的识别能力。此外，通过比较AMBFC算法与不同IMF 分量的癫痫检测结果，证明了相较于单个频段的信息，不同频段的信息的组合能够为脑电癫痫检测提供更多有效信息。

癫痫发作时，由于神经元动作电位发放的同步性，多通道脑电之间的信息流强度与非发作时相比存在显著差异［18］，而利用基于格兰杰因果的效应性连接分析方法可以有效地衡量不同脑区之间的交互性连接［24］，此前也有相关研究将DTF 算法应用于癫痫发作的检测和预测中［18，25］。因此，本研究利用DTF 算法做特征提取，提取不同脑电通道之间的流出信息，将此作为分类依据可以有效地区分发作期和非发作期的脑电信号。而且通过实验证明，利用PCA 降维保留原始特征数目的85%，可以达到更优的分类结果，表明了原始的特征数目过多，可能造成了分类器的过拟合。

同时，由于非发作期的样本数量远远多于发作期的样本数量，因此采用CSVM 进行分类，可以使得不同样本的误分类具有不同的代价［14］。为了综合考虑精确率和召回率，采用F2 值作为模型训练时的评估指标。根据网格搜寻方法，确认F2 值最高时惩罚因子C和惩罚因子调整系数w1 的取值，通常情况下参数w1 的取值大于1，表明相较于较多数量的非发作期样本，CSVM 算法赋予了较少数量的发作期样本更高的误分类代价，凸显出准确识别发作期的样本的重要性，从而改善了样本严重非均衡化带来的问题。

本研究从自适应多尺度脑功能连接的角度出发，提取不同频段脑区之间的信息流出强度，可有效区分发作期和非发作期的脑电，相较于传统算法达到了更高的精确率和召回率，在与新近提出方法的比较中也体现出了一定的优越性。但同时也具有一定的局限性，长期的头皮脑电记录中存在高频肌电伪影，会对实验结果造成一定的影响，另外，将全部脑电通道的信息流出强度作为有效特征，而未进行通道选择，不能为癫痫病灶的定位提供有力依据。

4 结论

本研究针对长时程脑电癫痫发作检测的问题，提出一种新的基于自适应多尺度脑功能连接的癫痫发作检测方法。通过结合MEMD 算法和MVAR模型，对具有非平稳特征的脑电信号提取流出信息强度，并进行特征组合与PCA 特征降维，最后经CSVM 分类区分发作期和非发作期脑电。本研究提出的算法在高准确率的基础上，达到了较高的精确率、召回率和F2 值，并具有一定优越性，有望应用于长时程脑电的实时监测。