非线性温度载荷下渐变齿高涡齿变形研究

赵 嫚，杨 洋，李 通，安雄雄

(兰州理工大学 石油化工学院，甘肃 兰州 730050)

1 引言

涡旋压缩机是继转子压缩机、往复压缩机、螺杆压缩机之后的又一种新型高效容积式压缩机，具有结构简单紧凑、体积小、重量轻、噪声低、运行平稳等优良特性，被广泛应用于制冷空调、机械等领域[1]。随着涡旋压缩机朝着高速、大气量和智能化方向的发展，研究涡旋压缩机涡齿结构以及涡齿的变形特点越来越受到关注。孟姜楠等[2]提出利用FANUC系统中的圆锥插补功能加工涡齿高度渐变的解决方案，实现了涡旋齿高度均匀渐变，改善了涡齿高度逐渐增高的加工效果；王君等[3]提出了一种高低间断涡齿，建立了间断齿在气体压缩过程中的数学模型；强建国[4]分析了涡齿的温度分布并建立了稳态温度场模型，对齿高变形进行有限元模拟，研究了齿高变形对压缩腔轴向密封的影响；Diniz M.C等[5]提出了一种集总参数热模型，用于预测涡旋压缩机内部不同腔室和部件的温度；QiangJianGuo，LiuZhengquan[6]利用涡旋齿稳态温度场，对不同参数和工况的涡齿模型进行有限元模拟，拟合得出涡齿端面齿高变形简化计算公式；王君等[7-9]通过建立涡旋压缩机涡齿的温度分布模型，研究了涡齿在温度和压力耦合下的受力和变形规律；羊玢等[10-11]建立涡旋压缩机动涡盘有限元模型，通过研究不同主轴转角的涡齿的刚度和强度，得到涡齿的变形和应力分布规律；Lin等[12-13]对涡旋压缩机内部温度和应力变形进行了研究。王建吉等[14]通过对动涡旋齿和动、静涡旋齿装配后在单场及多场耦合作用下强度进行分析，得到装配后涡旋盘的安装间隙对涡旋齿的变形存在干涉，单独分析动涡旋齿时的变形大于装配后的变形；孙笑[15]通过根据等效应力分布情况进行了涡旋齿高参数的优化，得到变齿高涡旋压缩机经过结构优化其性能和寿命可以达到相关国家标准要求。在已有的研究中，对动涡盘进行变形分析时都是假设涡齿温度沿展角呈线性变化，且对涡齿进行热变形分析时未考虑渐变齿高对变形的影响。

本文根据圆渐开线涡旋腔成对出现的特点、工作腔内气体的温度变化规律以及工作腔内气体间的换热特点，采用数值模拟与理论计算相结合的方法，分析了涡齿内外壁面温度的变化规律，并利用有限元软件Ansys Workbench对渐变齿高涡齿在非线性温度载荷作用下的变形进行了研究，得到球墨铸铁材料下涡齿的最佳渐变齿高范围，为涡旋压缩机的结构设计及加工装配提供一定的理论参考。

2 有限元模型的建立

考虑到温度引起的涡齿变形造成的齿头粘连，设计了沿涡齿中心齿顶向外环状递增的渐变齿高涡旋齿，建立的动涡盘三维几何模型如图1所示。动涡盘的几何参数为：基圆半径3.5 mm，动涡盘回转半径6.5 mm，初始齿高40 mm，吸气温度20 ℃，进口压力0.2 MPa，排气温度110 ℃，出口压力0.7 MPa。参照某动涡盘要求齿高从涡旋线展开230°至1040°渐变升高(18±3)μm[2]，设置沿涡齿中心齿顶向外环状递增的渐变高度分别为15 μm、16 μm、17 μm、18 μm、19 μm、20 μm。

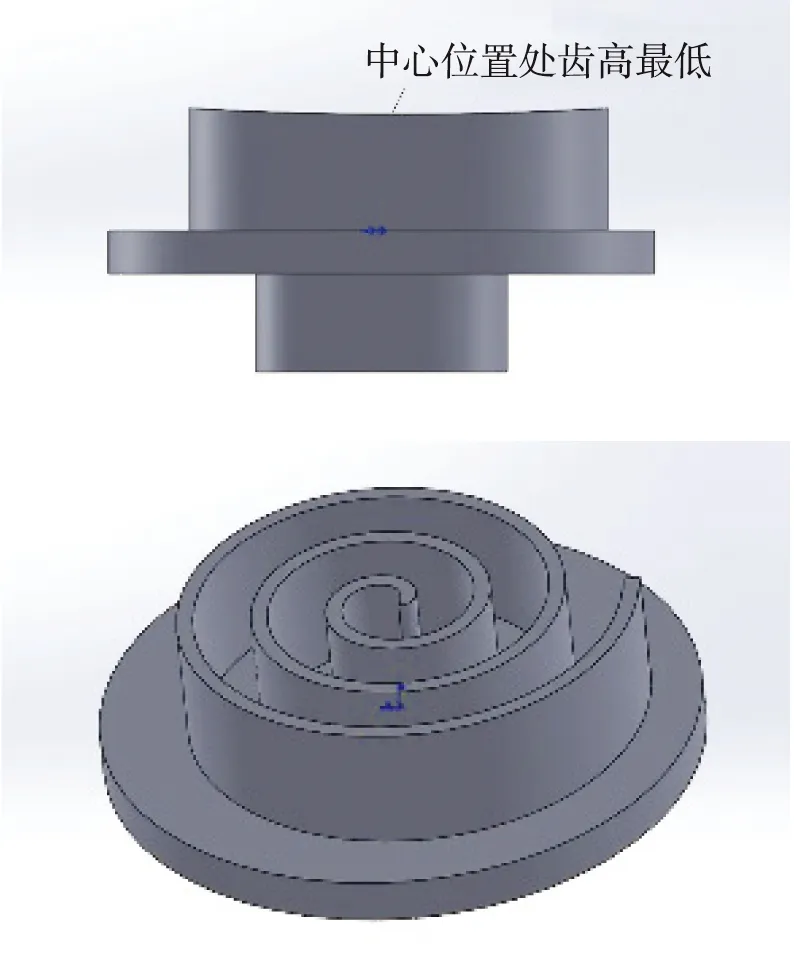
图1 动涡盘三维几何模型

在有限元分析中，网格类型采用扫描划分与六面体划分法，设置最小尺寸为2 mm，网格划分后的有限元模型共有77155个节点，单元数为502260，如图2所示。动涡盘材料选用球墨铸铁QT400，基本参数如表1所示。

图2 动涡盘有限元模型

表1 材料基本参数

3 动涡齿壁面温度的分布

3.1 动涡齿壁面温度的计算

涡旋压缩机工作特点是多对压缩腔同时工作，且同一涡齿内外壁面温度不同。为求得动涡齿壁面温度，需得到每个工作腔容积及压力变化规律。涡旋压缩机压缩腔工作容积表达式为

(1)

式中Rb——基圆半径

h——涡旋齿高

θ——主轴转角

α——渐开线起始角

φe——终止展角

规定自变量为主轴转角θ，根据能量守恒方程和理想气体状态方程，可以得到任一转角下压缩腔压力和温度随转角的变化关系

(2)

涡旋压缩机压缩腔内部气体的流态形式为湍流[16]，涡齿之间的对流换热方式为强制对流换热。涡齿壁面与工作腔内气体之间对流换热的热阻主要集中在热边界层，因此可以使用傅里叶导热公式求解涡旋压缩机涡齿的壁面温度

(3)

式中δ——热边界层厚度

λ——对流换热系数

T——某一转角处工作腔内的气体温度

Tw——涡齿壁面温度

q——热流密度

涡齿与工作腔内气体之间的对流换热模型如图3所示。

图3 涡齿与气体对流换热模型

3.2 任意转角处涡齿壁面的气体温度

图4为动、静涡盘啮合型线，涡齿外侧型线用ABCDE表示，内侧型线用abcde表示，外侧型线AB

图4 动、静涡盘啮合型线

和内侧型线de在工作过程中不参与啮合，因此称AB和de段为非啮合段，以B、d为分界点，其余部分都参与啮合。其中AB段始终接触吸气腔，其温度边界为：T=TS；de段始终接触排气腔，其温度边界为T=Td。

动涡齿外侧型线啮合段BE与涡齿内侧型线啮合段ad在同一转角时刻温度边界条件相同，温度随主轴转角变化规律的函数为T(θ)，由此可以得到任意转角时刻压缩腔内的气体温度随涡齿型线展角的变化规律。

外侧型线从起始展角φs到终止展角φe温度随主轴转角θ的变化函数为

(4)

内侧型线从起始展角φs到终止展角φe温度随主轴转角θ的变化函数为

(5)

式中θ1=180°，θ2=180°+900°，θ3=180°+900°+90°=1170°，因此涡齿展角范围(φe-φs)为θ∈[0，1170°]。

将T(θ)代入傅里叶导热公式(3)即得到涡齿内、外侧壁面所接触气体温度的等效温度函数Tw(θ)，如图5、图6所示。

图5 动涡齿内侧壁面温度分布

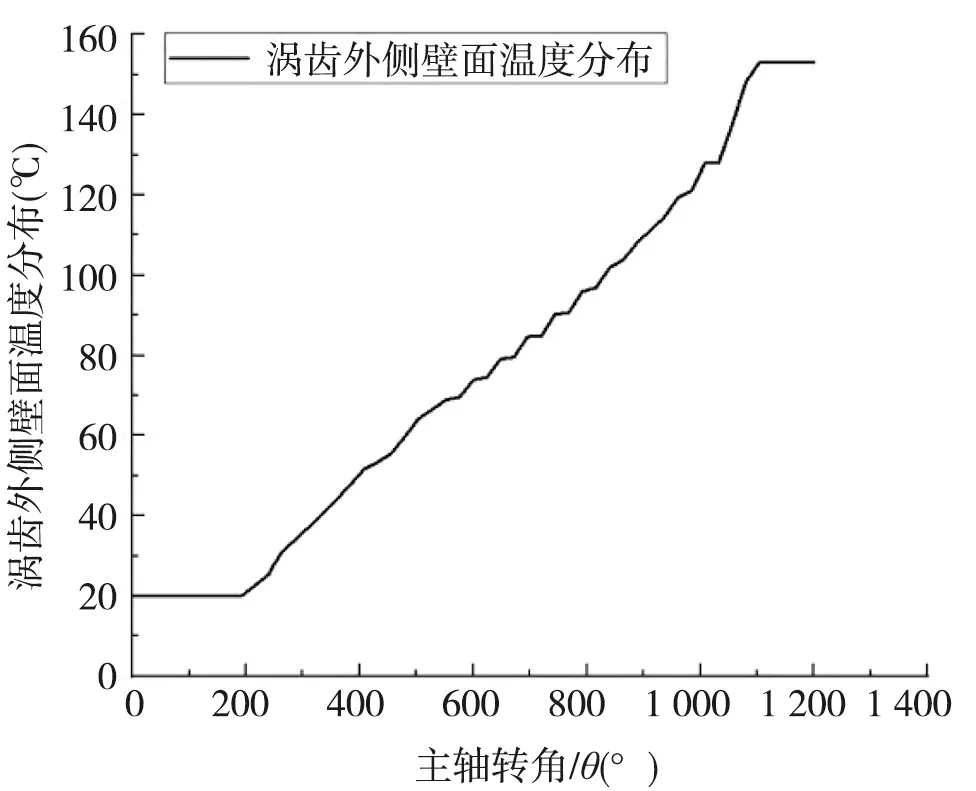
图6 动涡齿外侧壁面温度分布

由动涡齿内外侧壁面温度分布观察得到，内外侧壁面的温度分布整体趋势相似，均随主轴转角呈非线性变化，在涡齿外侧吸气腔和内侧排气腔的温度升高趋势较为平缓，内侧壁面的温度整体高于外侧壁面温度，两侧壁面存在温度差。

4 仿真分析

4.1 非线性温度载荷施加

采用Table型表格数据施加温度载荷。加载时以主轴转角θ为自变量X，以其相应位置处的温度载荷T为因变量Y。为了保证数据的加载均匀，利用Solidworks软件对动涡盘三维模型进行分割，沿基圆分割成15等份，如图7所示。

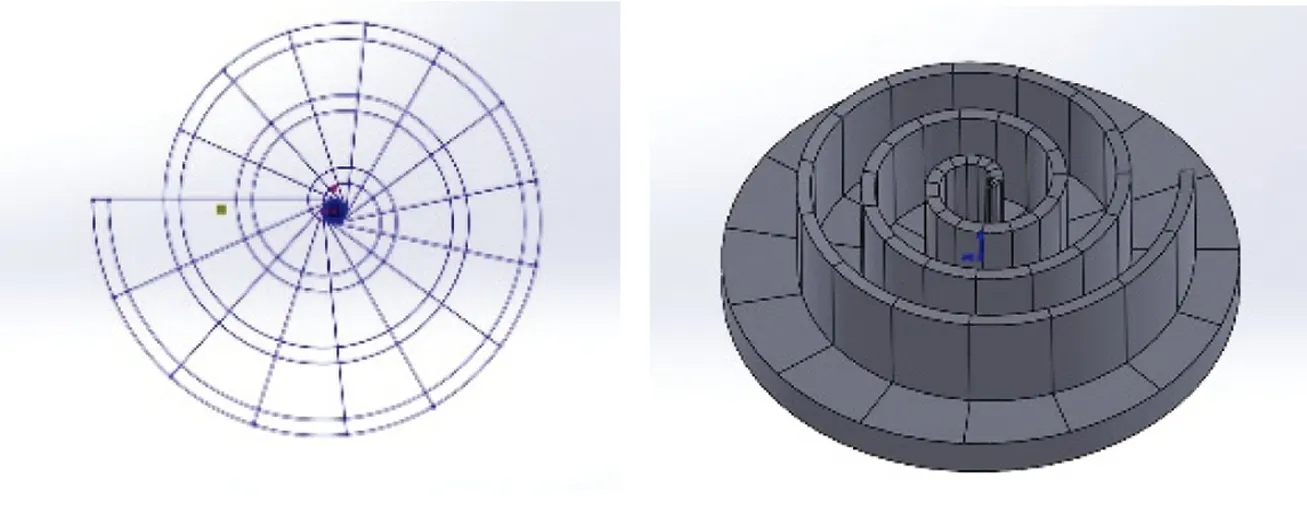
图7 动涡盘的切割划分

4.2 动涡盘的温度分布及涡齿变形特点

图8为动涡盘在非线性温度载荷下的温度示意图，涡齿内侧齿壁温度高于外侧齿壁温度，动涡盘底面温度沿涡旋中心向外近似呈环状减小。

图8 动涡盘温度分布

取沿涡齿中心齿顶向外环状递增的渐变高度分别为15 μm、16 μm、17 μm、18 μm、19 μm、20 μm。对不同渐变齿高的动涡盘模型进行非线性温度载荷施加，通过有限元分析获得非线性温度载荷下的涡齿变形，分析比较不同齿高下的仿真结果。

图9和图10分别为渐变高度15 μm的动涡盘在非线性温度载荷下的变形云图及涡齿变形量，可以看出涡齿最大变形发生在中心齿头处，变形量为15.107 μm，涡齿变形率为37.8%；最小变形发生在涡齿最外沿，变形量为0.264 μm。

图9 渐变高度15 μm的涡齿变形云图

图10 渐变高度15 μm的涡齿变形量

同样方法得到沿涡齿中心齿顶向外环状递增的渐变高度为16～20 μm的变形曲线，如图11所示，数据对比见表3。

图11 不同渐变齿高的涡齿变形量

表3 不同渐变高度的涡齿变形量

图11和表3可以看出，不同渐变高度下的涡齿变形规律基本一致，均随转角呈平缓升高的趋势；涡齿轴向最大变形发生在中心齿头处，变形量在15～16 μm之间。

对比五组渐变高度下的涡齿变形量，变形量均随转角呈平缓升高趋势，越靠近中心排气腔，气体温度越高，变形越大，最大变形均在15～16 μm之间。对比五组渐变高度下涡齿的变形率，可以得到球墨铸铁材料下由温度引起的涡齿变形率为38.3%。

5 结论

(1)涡齿壁面温度沿渐开线展开方向随转角呈非线性变化；

(2)球墨铸铁材料下沿涡齿中心齿顶向外环状递增的渐变高度在15～16 μm之间为宜；

(3)渐变齿高设计对温度引起齿头变形带来的粘连问题有一定的改进作用；渐变高度尺寸值的合理选用可防范结构设计上带来的径向泄漏问题。