基于实验 自主探究 发展素养
——“圆周角(1)”教学实录与反思
2022-11-24丁银杰江苏省苏州市草桥中学校215031
丁银杰 (江苏省苏州市草桥中学校 215031)
1 基本情况
1.1 教材内容分析
圆周角(1)是苏科版《义务教育教科书·数学》九年级上册第2章“对称图形——圆”第4节“圆周角”第1课时的内容,在本章的前3节学生学习了圆的有关概念,圆的对称性和确定圆的条件等知识,本节课学习圆周角的概念与性质.圆周角是本章的核心概念,是学习圆内接四边形,探究圆幂定理的重要基础,同时也是联系圆与三角形、四边形及相似形知识的纽带.
教材首先介绍了弧所对的圆周角概念,其次通过分别画90°,60°的圆心角对应的圆周角,并得出其分别为45°,30°,获得同弧所对的圆周角是圆心角一半的猜想,最后用分类与整合的方法证明圆周角性质,并通过例题教学加以巩固.
1.2 学生学情分析
施教对象为苏州市教育局直属初中校九年级学生,学业基础较好,经过七、八年级系统的数学实验教学,学生具有一定的实验探究、合作交流、分析整合的能力.根据儿童思维发展理论,九年级学生的思维以抽象逻辑思维为主要形式,但抽象思维水平仍然较低,对数学知识的理解还需要如实物学具、技术平台等直观形象的支撑.
1.3 教学目标设置
教学目标 (1)(知识与技能)认识并理解圆周角概念,了解并证明圆周角定理,能运用圆周角定理解决相关问题;(2)(思想与方法)在探索和证明圆周角定理的过程中,体会特殊与一般、分类与整合、转化与化归的数学思想方法,学会数学地思考;(3)(策略与途径)经历“观察—猜想—验证—证明—应用—拓展”的探索过程,发展数学抽象、直观想象、逻辑推理和数学建模等素养.
1.4 重点难点确定
教学重点 基于实物操作和技术探究构建圆周角概念,探索圆周角性质.
教学难点 从实物模型中抽象出圆周角概念,运用分类与整合,转化与化归的思想方法探索并证明圆周角性质.
1.5 教学策略选择
由于圆周角概念的抽象性,圆周角定理探索需要用到分类与整合的思想方法,本节课的教学采用实验探究的方式进行,教学中引入实物工具“圆周角探究仪”和技术工具GeoGebra,支持学生的自主探究,营造“做”数学的环境,帮助学生在实物操作的基础上构建概念,在技术探究中探索性质,发展素养.
2 教学过程
2.1 创设情境,激发兴趣
师:如图1,在一个圆形场地上,图中阴影部分是舞台,甲、乙、丙三位摄影师分别在C,D,E三点处对着舞台摄影.哪位摄影师拍摄的角度最大?哪位摄影师拍摄的角度最小?

图1
生:凭直觉,甲摄影师拍摄的角度最大,丙摄影师拍摄的角度最小(但不能明白其中的数学原理).
师:你的直觉是对的,学完本节课的内容,你就会知道其中的数学原理.
2.2 实验操作,构建概念
师:这节课我们采用实验探究的方式来学习,图2是一个学具,由一个直线轨道和一个圆形轨道组成,A,B为圆形轨道上的两个定点,动点P可以在直线或圆形轨道上自由滑动.

图2
(1)操作:分别沿学具的直线轨道和圆形轨道移动“动点P”;
(2)观察:在“动点P”移动的过程中,∠APB的顶点、两边与“圆”有怎样的位置关系?
生:当点P沿直线轨道运动时,∠APB的顶点可能在圆内、圆上或圆外,两边都与圆相交;当点P沿圆形轨道运动时,∠APB的顶点始终在圆上,两边都与圆相交.
师:当点P沿圆形轨道运动时,同学们发现 图3中的∠AP1B,∠AP2B,∠AP3B,它们有两个共同特征:它们的顶点都在圆上,它们的两边都与圆相交,这一类特殊的角就是本节课的研究对象——圆周角(板书课题),你能给圆周角下个定义吗?

图3
生:类比∠AOB,顶点为圆心,称为圆心角,可以这样定义圆周角:顶点在圆上,两边都与圆相交的角叫做圆周角.
师:概括得很好(板书定义).

请你根据圆周角定义,辨析图4中的角是否为⊙O的圆周角?为什么?
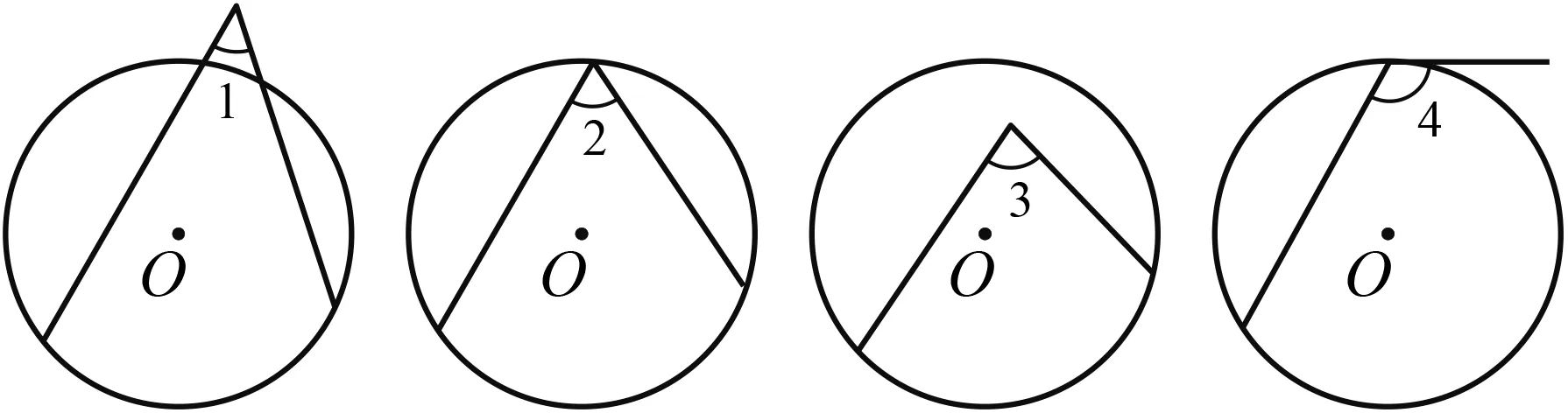
图4
生:∠1不是⊙O的圆周角,因为它的顶点在圆外;∠2是⊙O的圆周角;∠3不是⊙O的圆周角,因为它的顶点在圆内;∠4不是⊙O的圆周角,因为它的一边与⊙O不相交.
2.3 实验探究,探索性质
2.3.1操作与猜想
师:刚才通过实验操作,我们构建了圆周角概念,那么圆周角有怎样的性质呢?我们继续用实验的方式探究.
(1)操作:分别沿学具的直线轨道和圆形轨道移动“动点P”;
(2)思考:在“动点P”移动的过程中,∠APB的大小如何变化?
生:当点P沿直线轨道由圆内向圆外运动时,∠APB由大变小;当点P沿圆形轨道运动时,∠APB的大小不变,并且等于∠AOB的一半.
师:你是如何得到“当点P沿圆形轨道运动时,∠APB的大小不变,并且等于∠AOB的一半”的?
生:我是根据量角器测量的数据得到的,先量得圆心角∠AOB为100°,再在三个不同的位置量得圆周角∠APB均为50°.
师:同学们通过实验的方法得到了一个猜想:圆周角的度数等于它所对弧上的圆心角度数的一半,同弧所对的圆周角相等.
2.3.2验证与说理
师:这个猜想是否总是成立?我们再用技术验证一下.


图5
(2)拖动点C,改变点C的位置,观察∠AOB和∠ACB的度数的变化情况;
(3)拖动点B,改变点B的位置,观察∠AOB和∠ACB的度数的变化情况;
(4)拖动点A,改变⊙O的大小,观察∠AOB和∠ACB的度数的变化情况.
生:经过度量,动态观察,∠ACB的度数始终是∠AOB的一半.
师:我们借助技术更一般地验证了猜想,猜想要成为定理还需要证明,先来尝试证明下面的特殊情形.
(1)如图6,AB为⊙O的直径,C为⊙O上一点(不与A,B重合),试说明∠ACB=90°;

图6 图7

生:(利用三角形内角和定理解决上述问题,获得经验,具体过程略.)
师:以上我们证明了两种特殊情形:当圆心角为180°时,对应的圆周角为90°;当圆心在圆周角的一边上时,同弧所对的圆周角是圆心角的一半.圆心和圆周角还有哪些不同的位置关系?
生:(借助平板操作)还可能圆心在圆周角的内部或圆心在圆周角的外部.
师:如图8、图9,这两种情形更具有一般性,如何证明呢?

图8 图9

师:也就是说,在图8中,我们借助于添加直径,把一般情形转化成如图7的两个特殊情形的“和”,用同样的方法,图9这种情形可以转化成如图7的两个特殊情形的“差”,请同学们课后完成证明过程.这样我们就得到了圆周角的性质(板书):圆周角的度数等于它所对弧上的圆心角度数的一半,同弧所对的圆周角相等.


图10
2.4 变式训练,应用拓展
师:下面我们来看一组问题.
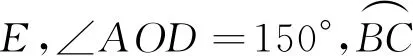
变式1 在图11中,连接AC,交BD于点F,则∠AFD=°.

图11 图12
变式2 如图12,⊙O中,点C在⊙O内,点D在⊙O上,点E在⊙O外(C,D,E在AB同侧).试比较∠ACB,∠ADB和∠AEB的大小,并说明理由.
教师巡视,学生先独立思考,再小组合作,班级交流,顺利解决例题和变式1,体会圆周角性质的应用价值,初步感受求“圆外角(∠AEB)”“圆内角(∠AFB)”中的转化与化归的思想方法.对于变式2,教师稍加提示后,学生也能继续通过添加适当的辅助线,将问题转化.
生:在图12中,设BE与⊙O交于点F,延长BC交⊙O于点G,连接AG,则根据圆周角的性质可得∠AFB=∠ADB=∠AGB.又因为∠AEB<∠AFB,∠AGB<∠ACB,所以∠AEB<∠ADB<∠ACB,
师:也就是说,在本课开头的问题情境中,甲摄影师拍摄的角度(∠ACB)最大,丙摄影师拍摄的角度(∠AEB)最小.
2.5 课堂小结,布置作业(略)
3 回顾与反思
3.1 教学设计的立意
本节课设计了两条主线,一条是基于知识的明线(情境—概念—定理—应用—拓展),学生以“做”为支架,用实验的方法自主探究,经历知识
发生、发展和应用的全过程,拓展思维广度和深度.
另一条是基于核心素养发展的暗线,素养立意主要体现在:(1)圆周角探究仪中的直线轨道、圆形轨道、橡皮筋等物化工具有利于学生抽象出圆周角概念,发展数学抽象素养;(2)从操作到猜想,从特殊到一般,定理探索的全过程充分运用了合情推理与演绎推理,有利于发展逻辑推理素养;(3)学具的直观、数据的直观和图形的直观,有利于学生获得猜想,突破思路,发展直观想象素养;(4)圆周角定理建立了一个“良构”的数学模型,圆内角、圆外角的探究是模型的自觉应用,发展了数学建模素养.
3.2 教学反思
(1)数学课堂要突出学生的主体地位
《义务教育数学课程标准(2011年版)》强调“动手实践”是学习数学的重要方式,要求“学生应当有足够的时间和空间经历观察、实验、猜想、计算、推理、验证等活动过程”[1],学生是学习的主体,课堂教学要以学生的“学习”为中心.基于实物学具圆周角探究仪的操作和基于技术工具GeoGebra的探究很好地体现了学生主体观,学生在操作中思考,在探究中辨析,具身参与认知过程,通过手脑协同,达到启思明理,从而构建新知,发展素养.教师的作用在于给学生设计适当的活动,提供适切的工具,进行适度的指导,帮助学生完成自主研究,发挥应有的主导作用.
(2)数学课堂要关注知识的来龙去脉
数学是严谨、系统的学科,每一个相对独立的知识都是数学体系的一个有机组成要素,我们不仅要关注它是什么,也要关注它来自何方,将走向何处.舞台的拍摄角度、足球射门的角度等是圆周角、圆内角和圆外角的生活起源,圆心角是圆周角、圆内角和圆外角的数学之根.借助圆周角探究仪的操作,圆心角生长为圆内角、圆周角和圆外角.基于技术的探究为用分类与整合、转化与化归的思想方法证明圆周角性质获得了突破口,例题的变式训练不仅巩固了新知,更能让学生体会知识的应用价值,变式拓展呼应情境,解决实际问题,蕴含模型思想.情境的创设引发学生用数学的眼光观察现实世界,问题的解决则是学生用数学的语言表达现实世界的最好写照.
(3)数学课堂要落实素养的发展指向
“立德树人”是数学课程的根本任务,主阵地是课堂,落脚点是发展学生学科核心素养.《普通高中数学课程标准(2017年版)》提出了要在学习数学和应用数学的过程中,发展学生的数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养的课程目标[2].因此,教学设计中不仅要重视知识目标的设置与达成,也要关注素养目标的指向与落实.尽管知识不等于素养,活动不等于素养,但素养的发展必须基于获取知识的活动过程.教师要通过指向素养的教学设计,给予学生足够的活动时间与空间,发展学生学科核心素养.本节课基于实验探究,自主学习,发展了学生的数学抽象、逻辑推理、数学建模和直观想象等素养.
