含多EH参与的电-气区域综合能源系统多能流收敛性调整*
2022-11-24彭寒梅贺玮煜苏永新
彭寒梅,贺玮煜,胡 磊,苏永新
(1.湘潭大学 自动化与电子信息学院,湖南 湘潭 411105;2.多能协同控制技术湖南省工程研究中心,湖南 湘潭 411105)
0 引言
综合能源系统(integrated energy system,IES) 是能源互联网的重要载体,集电能、天然气能源和热能等多能源的生产、输送与分配、转换储存和消费于一体,可实现不同能源之间的优势互补,提高能源的利用效率和可再生能源的渗透率,得到了广泛的研究与关注[1-3].根据空间尺度和系统规模,IES主要分为跨区级、区域及终端综合能源系统[4-5].电-气区域综合能源系统实现区域范围内的配电网、配气网、区域能量中心及其他区域能源系统之间的互补支撑.
电-气区域综合能源系统的能量中心是主要的电/气耦合环节,其能源耦合关系可用能源集线器 (energy hub,EH)来描述[6-7],文中称之为耦合元件EH.随着能源形态与规模的发展,电-气区域综合能源系统内多能源之间的耦合不断加深,耦合元件EH数量不断增加,各种形式的负荷不断加剧,导致容易出现能流计算不收敛的问题.目前,国内外针对IES多能流计算的研究大多集中于确定性、最优、概率多能流计算及其改进算法上[6-12].然而,对多能流计算不收敛问题的研究与文献较少.IES确定性多能流计算方法主要分为统一求解法[9-10]和分解求解法[8,11-12]两大类,均基于牛顿-拉夫逊法进行迭代求解.分解求解法是电气解耦下对各能源子系统能流分别进行求解,具有更好的收敛性.电网参数错误、注入数据不合理和计算算法局限性是导致电力系统潮流计算不收敛的主要因素[13-14].许多文献提出的牛顿类方法及其改进具有较好的计算能力和较大的收敛区间,已广泛应用于潮流计算;且电网参数均已经过多次校正.由此,实际工程中通常认为注入数据的不合理是造成潮流计算不收敛的重要原因.目前大多数研究集中在输电网的潮流计算收敛性调整方法上[15-17].文献[15]针对无功功率不平衡导致的输电网潮流计算不收敛,提出了一种基于搜索无功功率不足节点的节点类型转换的收敛性调整方法.文献[16]针对大电网潮流计算不收敛,提出了一种基于知识经验和深度强化学习的收敛性自动调整方法.文献[17]提出了一种基于改进直流潮流算法的输电网潮流计算收敛性自动调整方法.但上述文献针对输电网,且收敛性调整方法均根据高压电网的有功无功功率弱耦合特性.
从数学角度看,电-气区域综合能源系统多能流计算的本质是求解非线性方程组.对多能流计算不收敛进行调整,得到满足要求的多能流计算结果,文中称之为多能流收敛性调整.电-气区域综合能源系统中:(1)电力系统一般为中压配电网,不同于高压输电网,其输电线路参数中电阻值与电抗值接近,有功无功具有较强的耦合性,节点注入有功和无功功率的变化会共同影响状态变量节点电压的变化;(2)含天然气系统,且含耦合电、气能源的EH元件,导致多能流计算的状态变量和控制变量多且耦合关系较复杂.上述特点使得电-气区域综合能源系统多能流计算不收敛的机理及收敛性调整方法不同于高压输电网;此外,EH可运行于两种模式:以热定电(following the thermal load,FTL)和以电定热(following the electric load,FEL)[18-19].EH运行于FEL模式下可作为电力系统的平衡节点,可参与有功功率平衡调整,为多能流收敛性调整方式提供了新的途径.
本文针对注入数据不合理导致的电-气区域综合能源系统多能流计算不收敛问题,基于牛顿-拉夫逊法解耦求解,进行多能流计算不收敛的机理分析,提出含多EH参与的多能流收敛性解耦调整方法.首先分开对电力系统和天然气系统的能流计算进行收敛性判定,以及不平衡量类型与关键节点的识别;再提出3种收敛性调整方式,根据识别结果采用相应的调整方式:若为有功功率不平衡,采用EH平衡机调整方式;若为无功功率不平衡或轻微有功功率不平衡,采用电力节点类型转换调整方式;若为流量不平衡采用天然气节点压力调整方式.最后,算例应用结果与分析验证文中所提多能流收敛性调整方法的可行性和有效性.
1 多能流解耦求解分析
1.1 系统能流模型
电-气区域综合能源系统中的电力系统为配电网,其交流潮流模型的节点功率方程为
(1)
式中:PGi、QGi,PLi、QLi,Pi,Qi分别为电力节点i的电源出力,负荷,注入有功和无功功率;Vi为电力节点i的电压幅值;N为电力节点总数;线路导纳为Yik=Gik+jBik;δik=δi-δk,为电力节点i、k的相位差.
天然气系统主要包含气源、天然气管道、压缩机及气负荷.由流量连续性方程及节点压力与管道流量关系,得到天然气系统能流模型[19]为
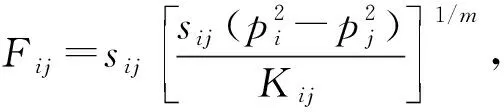
(2)
式中:A为节点-管道关联矩阵;F为管道流量向量;L为天然气节点气负荷向量;pi、pj为天然气节点i、j的压力;Kij为管道参数;m为流动指数;sij表征气体的流动方向,若pi>pj,则sij=1,否则sij=-1.
压缩机用来提高天然气节点压力以保证供气量,按所需功率来源不同可分为电压缩机和气压缩机,其所需功率为[19]
(3)
式中:Pc为压缩机所需功率;Fin为入口流量;po、pin分别为压缩机出口压力和入口压力;η为压缩机的效率;α为多变指数.
EH结构及能源耦合关系如图1所示,其结构内部包含电力变压器、微型燃气轮机和燃气锅炉.
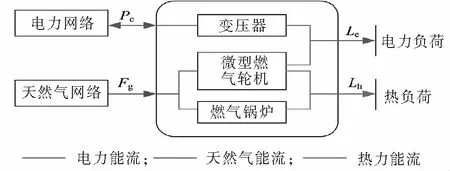
图1 EH结构及能源耦合关系Fig.1 The structure and energy coupling relationship of EH
EH结构及能源耦合关系计算模型为
(4)
式中:PEH、FEH分别为EH与电力系统、天然气系统交换的电力功率和天然气流量;ηe,MT、ηh,MT,ηT,ηGB分别为天然气经微型燃气轮机转化为电能和热能的转换效率,电力变压器和燃气锅炉的效率;vMT为天然气分配系数,0≤vMT≤1;Le、Lh分别为电力负荷和热负荷.
由式(1)~式(4)构成电-气区域综合能源系统多能流模型.
1.2 解耦求解分析
进行电-气区域综合能源系统多能流计算的节点类型处理[19]:(1)将电力系统的节点处理为电力平衡节点、PQ节点、PV节点;(2)将天然气系统的气源处理为气平衡节点,其余节点处理为气负荷节点;(3)将耦合元件EH进行解耦处理,对于天然气系统将其处理为气负荷节点;对于电力系统,将运行于FEL模式下且承担电力功率平衡的EH处理为电力平衡节点,其他情况下处理为PQ节点.
基于EH的节点类型处理,将含多EH的电-气区域综合能源系统进行电气解耦,进而可解耦求解多能流模型,其示意图如图2所示,EH在电力平衡节点下,先求解电力系统,再依次求解EH和天然气系统;EH在PQ节点下,先求解EH,再分开求解电力系统和天然气系统.
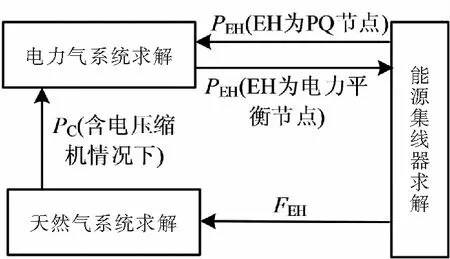
图2 多能流解耦求解示意图Fig.2 Schematic diagram of multi-energy flow decoupling solution
多能流方程可统一简写为
f(x)=0,
(5)
式中:f(x)为有功、无功功率、天然气流量函数矩阵;x为待求的状态变量向量.
从数学角度看,基于电气解耦的电-气区域综合能源系统多能流计算的本质是求解非线性方程组.电力节点的电压幅值和相位角、天然气节点的压力为待求的状态变量.EH在PQ节点和气负荷节点下,PEH、FEH取决于其电力负荷和热负荷,为不可控变量,节点电压幅值、相位角和节点压力为待求的状态变量;EH在电力平衡节点和气负荷节点下,电压幅值为控制变量,节点电压相位角、节点压力为状态变量.
2 多能流计算不收敛机理分析
2.1 节点实际注入值与不平衡量
牛顿-拉夫逊法是求解非线性方程组的常用方法,也是当前广泛采用的能流计算方法,但局限性是必须具备两个条件:合适的初值和雅可比矩阵非奇异.其求解式(5)的第k次迭代计算为
△f(k)=0-f(x(k))=J△x(k),
(6)
式中:△f(k)、△x(k)分别为第k次迭代的有功功率、无功功率、天然气流量的不平衡量的列向量,状态变量修正量的列向量;J为函数f的雅可比矩阵.
电-气区域综合能源系统多能流计算中的实际注入数据为电力节点的电源出力、负荷有功和无功功率值及天然气节点的气源出力、负荷流量值.由多能流模型可知,式(6)中的f(x(k))为第k次迭代下节点注入有功功率、无功功率、天然气流量的迭代计算值与实际注入值的差值.
牛顿-拉夫逊法求解式(5)的迭代过程为:将x(k)作为迭代初值代入f(x)函数,得到f(x(k)),进而得到不平衡量△f(k)和J的值,再由式(6)计算得到状态变量的修正量△x(k),从而求得状态变量的新值x(k+1)=x(k)+ △x(k),重复上述计算过程,最后可获得对式(5)足够精确的解,即在满足精度要求下有f(x(k))=0,△f(k)=0,代表节点注入有功功率、无功功率、天然气流量的迭代计算值等于实际注入值;而当其差值无法满足精度要求时,需进行反复迭代.由此,除牛顿-拉夫逊法本身的问题外,导致电-气区域综合能源系统多能流计算不收敛的主要原因是系统电力有功、无功功率不平衡、天然气流量不平衡,即f(x(k))≠0.
2.2 功率不平衡与能流计算不收敛分析
配电网两节点等值电路模型如图3所示,设电力节点1、2的电压分别为V1∠0、V2∠δ12,节点2的注入有功、无功功率分别为P2、Q2,阻抗Z12∠θ12=R+jX,阻抗电压降为dV12,纵分量为△V12.
dV12随着负荷的增加而增大,当增大到与V2相等时,系统达到稳定运行的极限[20],此时图3(b)为以V1为底边的等腰三角形,则有△V12=V1/2.由此,当电压降纵分量大于电力节点1电压幅值的1/2时,即为式(7),系统失去静态稳定性的必要条件,这种情况下,能流无解,进而能流计算不收敛.
(7)
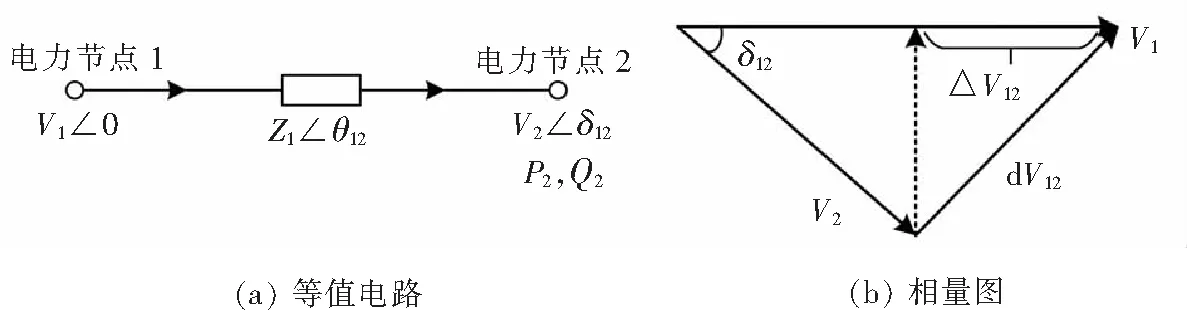
图3 两节点等值电路及其相量图Fig.3 Equivalent circuit and phasor diagram of two-node
功率不平衡具体表现为部分节点功率不足.设电力节点1电压V1稳定,有功和无功功率充足,即P2≥ 0、Q2≥ 0,由式(7)可进一步分析出:
(1)节点2的无功功率充足即能满足其负荷所需无功功率时,不需从配电网获取无功功率或获取无功功率较小,Q2减小,使得△V12 (2)由于中压配电网输电线路参数R/X约为1,因此,当节点2的无功功率不足时,Q2增大,可通过减小从配电网获取的有功功率P2,使得△V12 (3)当节点2的有功功率特别不足时,则P2特别大,即使使得Q2减小至0,仍有△V12>V1/2.这种情况下,单纯补偿无功功率已无法使得有功功率平衡,需要通过有功功率分摊等其他手段使能流有解.电力节点2的无功功率特别不足时同理. (4) 节点2的有功或无功功率不足但节点1电压较大时,也可能使得△V12 设两节点天然气系统的节点1、2压力分别为p1、p2,节点2气负荷为L2,根据式(2)可得 (8) 式中:△F2为天然气节点2的流量不平衡量;φ为天然气节点1、2的管道流量函数. 式(8)中,当流量不平衡量△F2=0,能流收敛.设节点1压力p1稳定,当L2增大时,由式(8)可知,为了使得△F2=0,必须使p22减小.若L2增大至p2小于规定的系统最低压力限制pmin时,流量不平衡量△F2=φ(p12-pmin2) -L2≠0,则能流不收敛.则需通过提高p1,使得△F2=0. 由牛顿-拉夫逊法迭代计算过程可知,当|△f(k)|逐渐趋于减小时,说明在该迭代过程中有功、无功功率、天然气流量的迭代计算值正逐渐向其实际注入值逼近,由此△f(k)较△x(k)更具有明确的实际意义.文中提出由|△f(k)|的最大值|△f(k)|max进行能流计算收敛性的判定,及进行导致不收敛的不平衡量类型与关键节点的识别,具体如下: (1)分开对电力系统和天然气系统的能流计算进行收敛性判定,及导致不收敛的不平衡量类型与关键节点的识别. (2)当|△f(k)|max在迭代过程中逐渐减小并最终减小至满足计算精度ε1要求时,则能流计算判定为收敛;当|△f(k)|max出现振荡并在规定的迭代次数下始终无法减小至满足计算精度ε1要求时,能流计算判定为不收敛. (3)多能流计算不收敛下,取迭代计算过程中|△f(k)|max最小的一次迭代,该次迭代计算值最接近于实际注入值.对于电力系统,若|△f(k)|max为有功不平衡量,则认为能流计算不收敛的关键因素为有功功率不平衡;若|△f(k)|max为无功不平衡量,则认为关键因素为无功功率不平衡.对于天然气系统,能流计算不收敛下|△f(k)|max为流量不平衡. (4)取迭代计算过程中|△f(k)|max最小的一次迭代,再取该次迭代中|△f(k)|> |△f|max×d%的节点(d为设置的常数),这些节点上的不平衡量较大,则认为其是导致不收敛的关键节点. 含多EH的运行模式及基于多能流计算不收敛的机理分析,文中提出3种多能流收敛性调整方式:EH平衡机调整方式、电力节点类型转换调整方式和天然气节点压力调整方式.根据识别出的不平衡变量类型与关键节点采用相应的调整方式. 3.2.1 EH平衡机调整方式可设置处于FEL工作模式的EH运行于电力平衡机状态,以平衡电力系统有功功率.有功功率不平衡下通过设置EH平衡机参与多能流收敛性调整.给定EH平衡机节点的电压幅值,相位角为待求的状态变量,称该节点类型为V节点.含m个EH平衡机节点会增加m个待求状态变量,为进行能流计算需增加m个方程;同时,某些电力平衡机出力可能越限.为此,设置出力比例以约束各电力平衡机的出力.当系统中有2个电力平衡机k、j时,令其出力成一定比例,即PGj=cjPGk,cj为出力比,0 PLj+Pj(x)=cj(PLk+Pk(x)), (9) 式中:PLk、PLj,Pk(x)、Pj(x)分别为电力平衡机节点k、j的负荷有功功率和注入有功功率;x的意义同式(5). 电力系统增加m个EH平衡机时,增加类似于式(9)的m个功率方程.通过改变cj值可分配各电力平衡机之间的出力比. 3.2.2 电力节点类型转换调整方式由多能流计算不收敛的机理分析可知,配电网中有功功率与无功功率共同影响系统电压的大小,无功功率不平衡或轻微有功功率不平衡下,可通过补偿电力节点无功功率来进行收敛性调整.提出的电力节点类型转换调整方式为:首先进行不平衡量类型识别,并寻找导致不收敛的关键PQ节点;再将寻找到的关键PQ节点设置为PV节点,电压幅值设置为1 pu,进行能流计算;最后将设置的PV节点恢复为PQ节点,将其作为PV节点时计算得到的注入无功功率作为补偿量进行补偿. 3.2.3 天然气节点压力调整方式天然气系统能流计算不收敛通过天然气节点压力调整方式来调整. (1)首先识别出导致不收敛的关键天然气节点,得到关键节点j及此时的迭代次数k. (2)再由式(10)计算得到天然气节点j的压力调整量δpj. (10) 式中,pj为天然气节点j在第k次迭代时的压力计算值. (3)由天然气节点j的压力供给者(就近压缩机或气源)提供压力调整量δpj,压力供给者的出口压力需调整为 (11) 式中:ps*为气源或压缩机调整后的出口压力;ps为气源或压缩机调整前的出口压力. 电-气区域综合能源系统多能流收敛性调整的流程如图4所示,对电力系统和天然气系统能流计算收敛性进行解耦判定与调整,具体步骤如下: (1) 读取系统数据,进行电力系统能流求解,若其能流计算不收敛,则转到步骤(2);若收敛则转到步骤(3). (2) 电力系统能流收敛性调整:进行不平衡量类型与关键节点的识别,若为有功功率不平衡,则采用多EH平衡机调整方式,若为无功功率不平衡或轻微有功功率不平衡,则采用电力节点类型转换调整方式,直到能流计算收敛. (3) 由电力系统能流计算结果和EH能流模型,计算EH天然气耗量. (4) 求解天然气系统能流,若能流计算不收敛,则转到步骤(5),否则转到步骤(6). (5) 天然气系统能流收敛性调整:进行能流不收敛关键节点的识别,采用天然气节点压力调整方式,直到能流计算收敛. (6)判别是否含有电压缩机.若含有电压缩机,则计算其耗电量,若先后两次耗电量之差不满足精度要求,则将此部分耗电量作为电力系统负荷,重新求解电力系统能流直至整个系统多能流计算收敛,并输出结果;若不含有,则输出计算结果. 图4 多能流收敛性解耦调整流程图Fig.4 The flow diagram of multi-energy flow convergence decoupling adjustment method 在配置为i7处理器、12GB RAM的计算机上,采用软件Matlab R2020a,编制文中提出的电-气区域综合能源系统多能流收敛性调整方法的程序. 设置电-气区域综合能源算例系统包含33节点电力系统、14节点天然气系统[21]和耦合元件EH,拓扑结构如图5所示,初始负荷和EH参数见附录表.电力系统中,电力节点1连接外部主网,DG1~DG4为不可控分布式电源,为PQ节点.天然气系统中,天然气节点1为气源,天然气节点5、8之间配置1台恒出口压力的气压缩机,由电力节点9供电,天然气节点7、10之间配置1台恒出口压力的电压缩机,由电力节点14供电. 设置标准状态下天然气流动指数m为2,压缩机的效率η为0.8,多变指数α为1.27,天然气节点最低压力pmin限制为0.8 MPa.设置电力系统基准容量为100 MW,参考相位角为0 rad,电压幅值合理区间为[0.90,1.10]pu;天然气节点1的初始压力为4 MPa,恒出口压力的压缩机的初始压力为3 MPa.设置合适的初值,采用牛顿-拉夫逊法对电-气区域综合能源算例系统初始负荷下进行多能流解耦计算,计算收敛,可得到多能流计算结果. 图5 电-气区域综合能源系统算例拓扑图Fig.5 Topological diagram of the electricity-gas regional integrated energy example system 对电-气区域综合能源算例系统设置:Case1为初始电力系统负荷有功功率增大4倍,其他不变;Case2为初始电力系统负荷有功功率增大6倍,其他不变;Case3为初始电力系统负荷无功功率增大8倍且天然气系统气负荷增大2倍,其他不变.设置合适的初值,采用牛顿-拉夫逊法对Case1~ Case3进行多能流解耦计算,计算均不收敛,得不到多能流计算结果. (1)Case1下电力系统能流计算前20次迭代中各次迭代的最大不平衡量如表1所示.由表1可知,第6次迭代的|△f|max最小,为无功功率不平衡量,则认为不收敛的关键因素为无功功率不平衡.第6次迭代的各电力节点无功功率不平衡量如图6所示,识别出导致不收敛的关键节点为电力节点8、9、12.而Case1下是有功负荷过重.验证了电力节点注入数据不合理会导致迭代计算中有功或无功不平衡,使得能流计算不收敛.同时表明了配电网有功无功具有强耦合性,使得当实际注入的负荷有功功率增加时,会导致节点电压值的变化,进而可能导致节点无功功率的迭代计算值与实际注入值存在较大差值. 表1 Case1下前20次迭代的|△f|max 图6 第6次迭代的电力节点无功功率不平衡量Fig.6 Node reactive power unbalance in the 6th iteration (2)Case2下电力系统能流计算前20次迭代中最小的|△f|max为第2次迭代的有功功率不平衡量,其值为0.967 4 pu,则认为不收敛的关键因素为有功功率不平衡. (3)Case3下电力系统能流计算前20次迭代中最小的|△f|max为第5次迭代的无功功率不平衡量,其值为0.156 4 pu,则认为电力系统能流计算不收敛的关键因素为无功功率不平衡;并识别出导致不收敛的关键节点为电力节点5、29、30.Case3下天然气系统能流计算前20次迭代中第19次迭代的|△f|max最小,此次迭代下的天然气节点压力计算值如图7所示.图7中,天然气节点5压力最小,为-4.681 0 MPa,远远低于系统的最低压力限制,是造成天然气系统能流计算不收敛的关键节点. 图7 第19次迭代的天然气节点压力Fig.7 Natural gas node pressure in the 19th iteration (1)采用本文提出的电力节点类型转换调整方式进行Case1下的收敛性调整.经计算,电力节点8、9、12需补偿的无功功率分别为1.814 4 pu、2.171 8 pu、4.176 7 pu.对收敛性调整后的Case1系统进行多能流计算,其电力系统节点电压幅值计算结果如图8所示. 由图8可知,调整后系统多能流计算收敛,且计算出的各电力节点的电压幅值均在合理范围内.表明本文提出的多能流收敛性调整方法只需根据识别出的导致不收敛的不平衡变量类型和关键节点采用相应的调整方式,适用于有功无功具有强耦合性的系统,验证了所提方法的可行性和有效性. 图8 收敛性调整后的Case1系统电压幅值计算结果Fig.8 The voltage amplitude results of convergence adjusted Case1 system (2)采用本文提出的方法进行Case3下的收敛性调整:①首先采用电力节点类型转换调整方式,经计算,关键电力节点5、29、30需补偿无功功率分别为8.025 8 pu、3.281 3 pu、5.568 0 pu;②再采用天然气节点压力调整方式,对天然气节点5的压力进行调整,计算得到调整量为4.748 9 MPa,所需调整的压力由节点5的就近压力供给者天然气节点1(气源)提供,计算得到天然气节点1调整后的压力为6.209 0 MPa,且电压缩机消耗有功功率0.099 5 pu.对收敛性调整后的Case3系统进行多能流计算,计算结果如图9所示. 图9 收敛性调整后的Case3系统多能流计算结果Fig.9 The multi-energy flow calculation results of convergence adjusted Case3 system 由图9(a)可知,计算出的各电力节点的电压幅值均在合理范围内;由图9(b)可知,Case3下天然节点压力值均高于pmin,满足要求.上述调整结果及其分析,表明电-气区域综合能源系统的多能流计算收敛性可以采用解耦判定与调整,简化了含电气耦合关系的多能流收敛性调整,验证了所提方法的可行性和有效性. 采用文中提出的EH平衡机调整方式进行Case2下的收敛性调整.将FEL工作模式下的EH3与EH4运行于电力平衡机状态,设置其电力节点电压幅值均为1.02 pu,电力平衡机出力比为0.5.对收敛性调整后的Case2系统进行多能流计算,计算结果如图10所示.为提供EH3与EH4的有功出力,由EH能流模型可计算出其所连接的天然气节点9、11均需增加天然气流量为6.088 7×104m3/h.图10(a)中,电力平衡机EH3(电力节点9)与EH4(电力节点14)有功出力均为3.644 2 pu,电力平衡节点1平衡有功出力为7.288 4 pu,各电力平衡机之间的出力符合设定的出力比. 图10(b)中,各天然气节点压力有解且均高于设置的pmin,满足要求.电压缩机消耗电功率为0.072 3 pu,电力系统负荷增加量较小,不影响其收敛.上述调整结果及其分析,表明电-气区域综合能源系统中的EH可参与多能流收敛性调整,验证了文中所提方法的有效性. 图10 收敛性调整后的Case2系统多能流计算结果Fig.10 The multi-energy flow calculation results of convergence adjusted Case2 system 文中针对电-气区域综合能源系统多能流计算不收敛的问题,分析出多能流计算不收敛的机理,提出含多EH参与的多能流收敛性解耦调整方法.算例结果及分析表明: 1)提出的不平衡量类型与关键节点的识别方法,考虑了迭代计算中变量的变化特征及实际意义,能识别出导致电力系统和天然气系统能流计算不收敛的关键因素与关键节点.该方法可解决有功无功强耦合给能流计算不收敛因素诊断及其调整带来的困难,且可为含多耦合元件多能流系统的多能流计算不收敛因素识别提供新的思路与方法. 2)提出的多能流收敛性调整方法对电力系统和天然气系统能流计算收敛性进行解耦判定与调整,且只需根据识别出的不平衡变量类型和关键节点采用相应的调整方式,提出的EH电力平衡机调整方式考虑了EH不同运行模式的特性.该方法有较好的收敛性调整效果,且简化了含多耦合节点的多能流系统收敛性调整,具有一定的工程实用性. 区域综合能源系统多能流收敛性的人工智能调整方法将是下一步的研究重点.2.3 流量不平衡与能流计算不收敛分析
3 多能流收敛性调整方法
3.1 不平衡量类型与关键节点的识别
3.2 收敛性调整方式
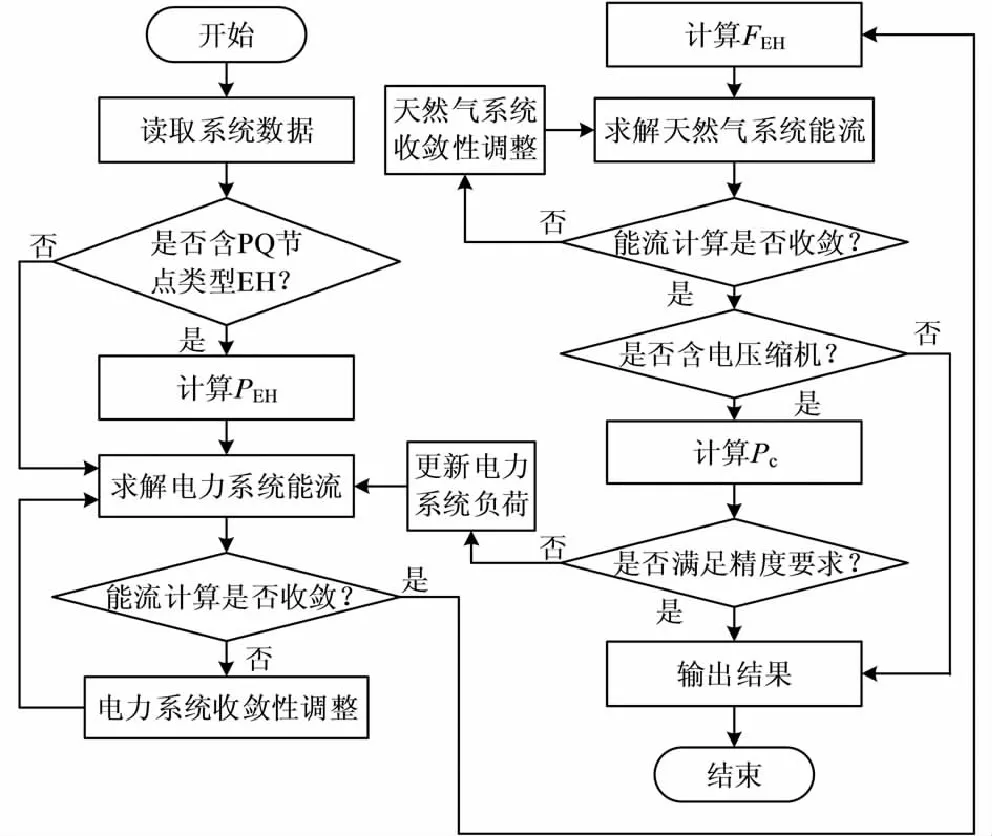
3.3 系统解耦调整流程
4 算例分析
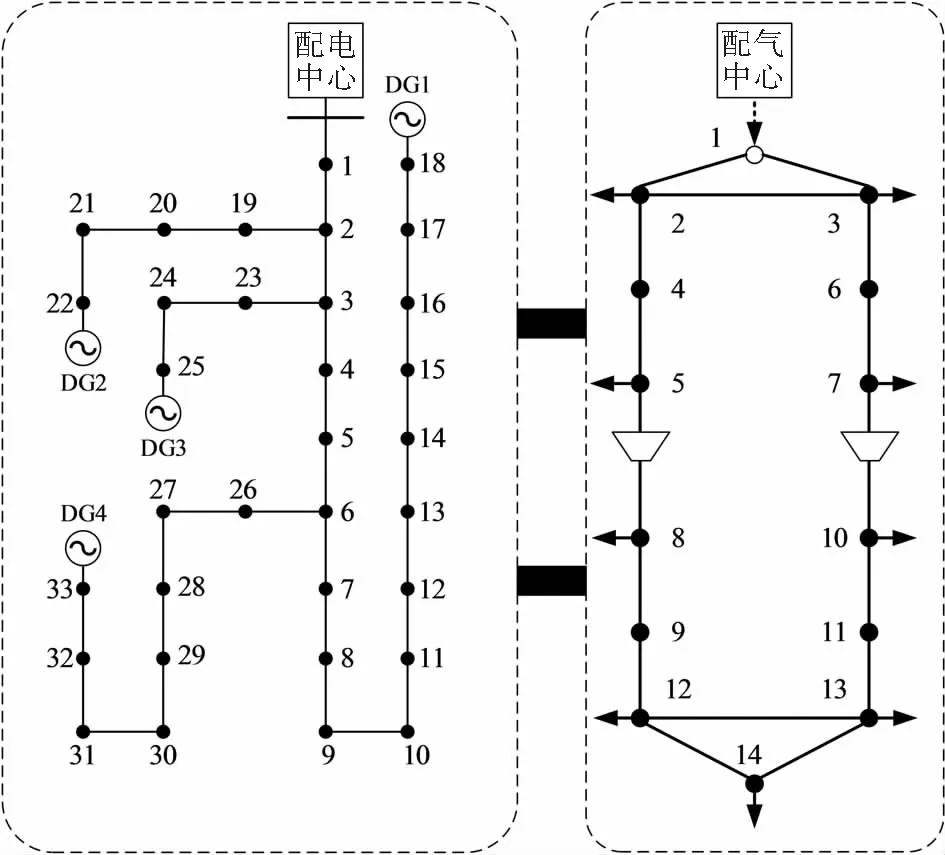
4.1 算例系统
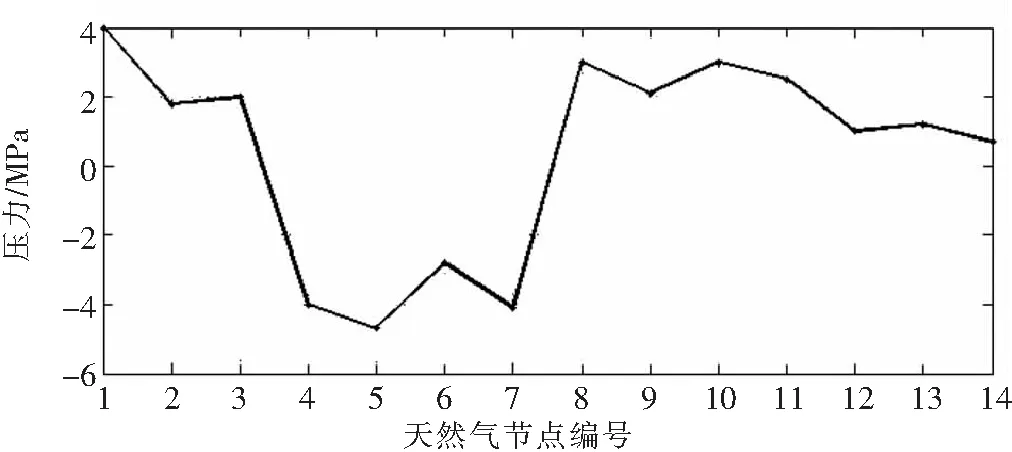
4.2 不平衡量类型与关键节点的识别结果


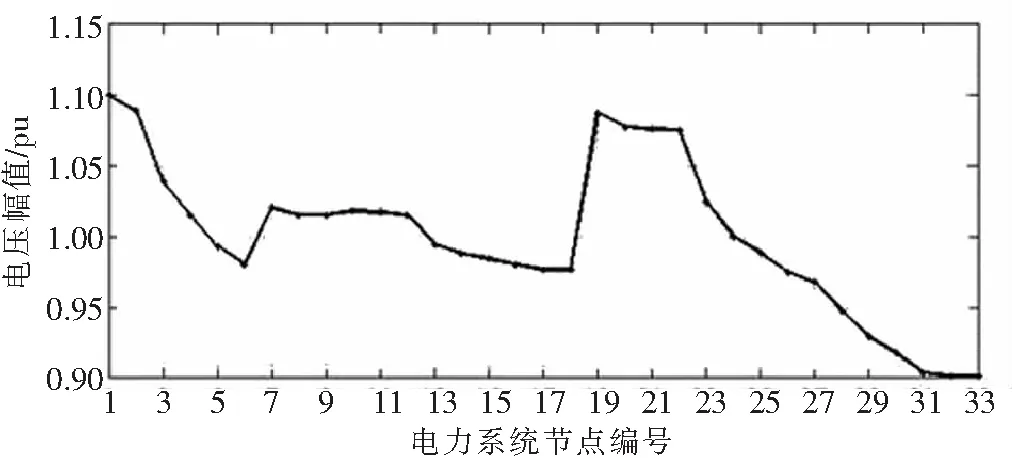
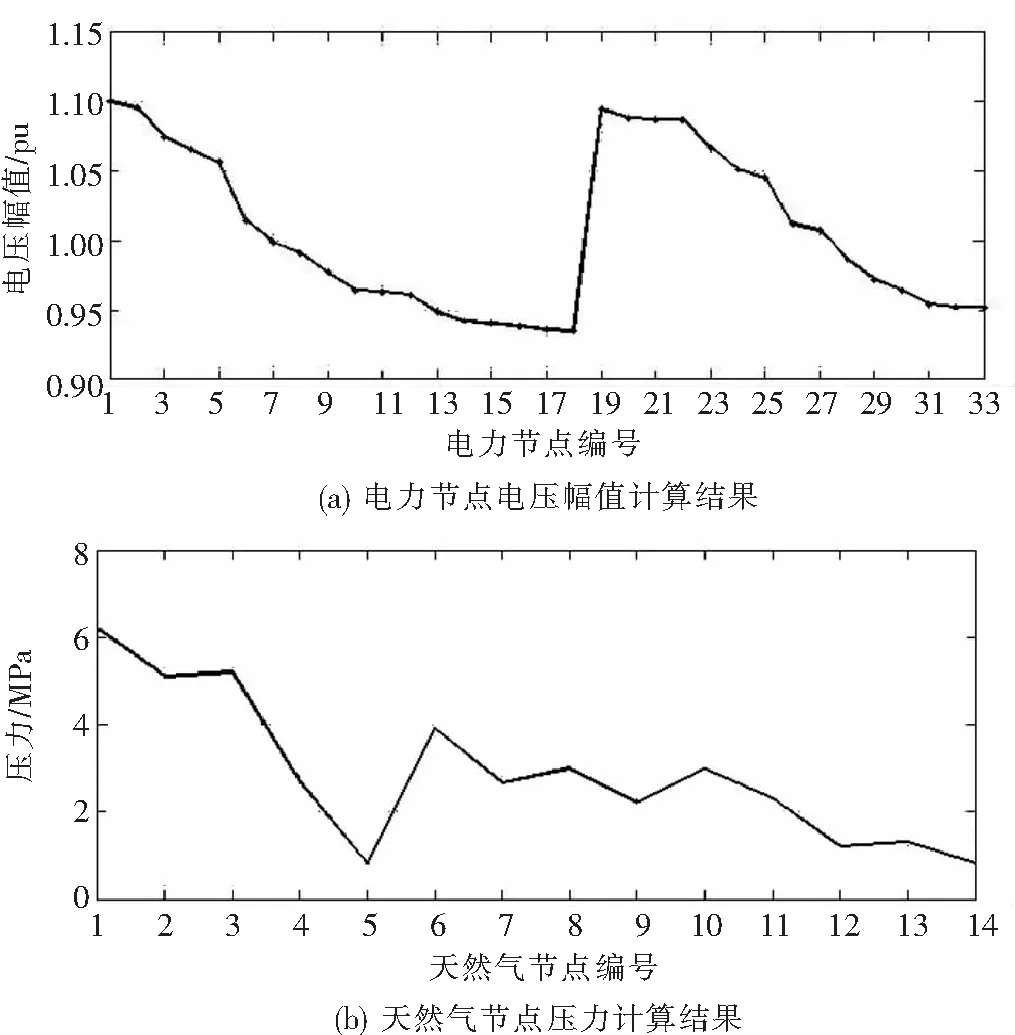
4.3 无功功率与流量不平衡下的能流收敛性调整
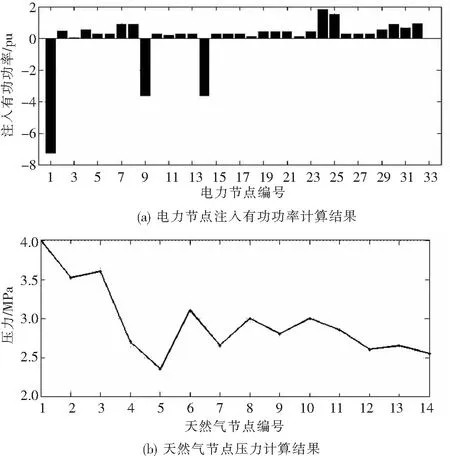
4.4 有功功率不平衡下的能流收敛性调整
5 结论
