BP优化PI与无源控制的并网逆变器复合控制

徐倩，张巧杰，王久和

(北京信息科技大学 自动化学院，北京 100192)

0 引言

在拓扑结构一定的情况下，并网逆变器的性能取决于控制策略[1]。传统控制方式为电压电流比例积分(proportional integral，PI)双闭环控制，外环PI控制器控制电容两端电压，其输出为电流内环PI的输入，同时内环PI实现电流解耦控制。但PI参数难以整定，无法实现真正的电流解耦。此外PI控制器需要建立精确的系统模型，当外界发生扰动时更是难以达到逆变器并网要求。因此，研究者们不断探索控制逆变器的新型策略从而提高逆变系统的性能。文献[2-3]采用无差拍控制内环，实现了并网电流快速跟踪，但需要建立精确的系统模型。文献[4]针对系统动态响应缓慢，提出PI+重复控制的复合策略对系统进行控制，但重复控制器本身动态较差，因此文献[5]又加入了模糊控制，对PI控制器进行优化从而提高其响应速度。文献[6-7]使用滑模控制器对逆变器进行控制，提高了并网电流控制精度，加强了鲁棒性，此控制虽提高了稳定性，但其控制器结构复杂。

无源控制(passivity-based control，PBC)具有良好的鲁棒性与动态性能，无源理论已成功应用到各种电力电子变换中。文献[8-9]采用PBC对光伏并网逆变器进行解耦控制，加强了系统的鲁棒性。为提高系统输出稳定性，文献[10-12]将PBC分别应用到Boost变换器、Cuk变换器中。文献[13-14]分别将PBC与PI控制、滑模控制相结合，提高了变换器输出电流控制精度。

神经网络作为智能控制中的一种，不需要建立精确的模型且具有较强的抗干扰性，可描述复杂的非线性系统，因此被广泛应用到各个领域。文献[15-16]采用反向传播(back propogation，BP)神经网络算法对并网逆变器电流环进行控制，较好地完成了并网电流跟踪，提高了系统动态响应。文献[17]采用BP-比例积分微分(proportional integral differential，PID)控制Boost变换器，降低了输出电压的过调，提高了系统的稳定性。文献[18]采用基于模糊神经网络的PI双闭环控制，对PI控制器进行优化从而提高其响应速度，电压外环采用模糊神经网络控制，来补偿电流内环精度，使得输出电流波形稳定。

为降低并网电流谐波，本文采用PBC对电流进行控制，由于PBC不能精确趋于稳定点，引入BP神经网络对PI外环进行优化设计，来补偿电流内环精度以加快电流内环的响应。该控制策略可消除并网电流稳态误差，快速跟踪电网电压，且电流谐波含量即总谐波失真(total harmonic distortion，THD)达到并网要求。仿真验证了该策略具有很好的控制效果。

1 并网逆变器拓扑结构

三相并网逆变器的拓扑结构如图1所示。L1为电感器电感，VT为开关管，VD为二极管，C为电容器的电容，L为滤波电感器的电感，R为滤波器阻抗和线路阻抗，ia、ib和ic代表逆变器并网电流，uea、ueb和uec为电网交流电压，udc为直流母线电压，iin为直流侧输入电流。

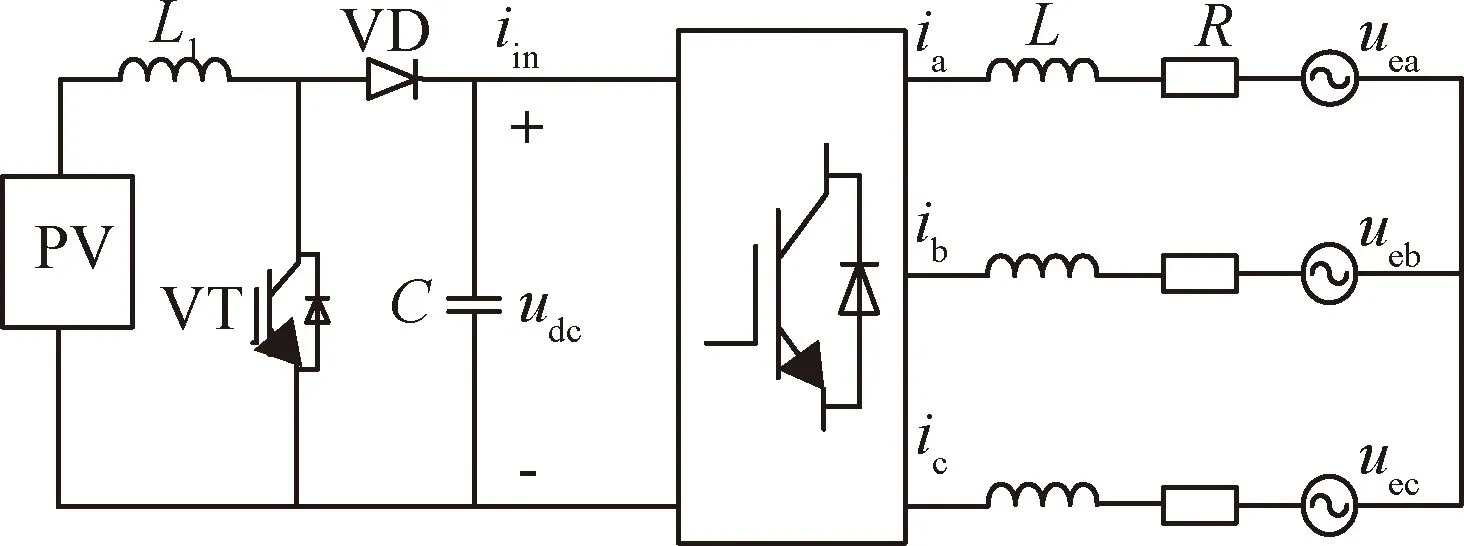
图1 三相并网拓扑结构

设该电路工作在平衡状态下，且电感为线性，开关无损耗，电容无损，该逆变器经矩阵变换转换到dq坐标系下的数学模型为

(1)

式中：Sd、Sq为开关函数在d、q轴上的分量；id、iq为逆变器并网电流在d、q轴上的分量；ued、ueq为电网交流电压在d、q轴上的分量；ω为两相旋转角频率。

2 复合控制器设计

2.1 PBC控制器设计

将式(1)写成表达式语言(expression language,EL)的形式：

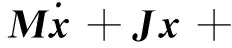
(2)

式中：M、J、分别为正定的对角阵、反对称矩阵、对称正定矩阵。即

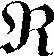
如果存在一个正定函数Q(x)以及半正定且连续可微的存储能量函数H(x)，可以得到耗散不等式：

H(x)≤uTy-Q(x)

(3)

式中,uTy为能量供给率。

设该系统能量函数为

(4)

则有

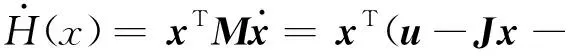
由于J=-JT，因此储存函数xTJx=0，结合式(3)，说明该系统是无源的。

设系统的误差存储函数为

(6)

定义参考状态变量为

为加快收敛速度，需注入阻尼，设阻尼耗散项：

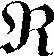
式中：

由式(2)可知：

(7)

令

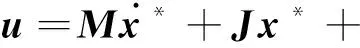
(8)

则使式(7)右边为0，即

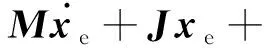
(9)

那么可使

(10)

根据式(8)可得开关函数为

(11)

将式(11)代入式(1)可得

(12)

将式(7)改写为

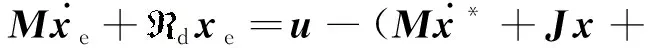
(13)

选择控制律：

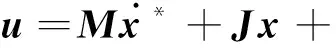
(14)

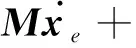
(15)

2.2 BP优化PI控制器设计

选择合适的阻尼，电流id会很快收敛到期望值。由于PBC不能使电流id精确趋于期望值，会降低微电网并网时的入网电流质量。本文设计了BP神经网络优化的PI控制器为电压外环来补偿电流精度，以此加快内环的响应速度消除稳态误差。设i、j、l分别为输入层、隐含层以及输出层神经元个数。BP神经网络输入层为实际电压udc、参考电压udcr以及两者的误差e，输出为PI控制器的比例系数kp、积分系数ki。三层BP神经网络结构如图2所示。

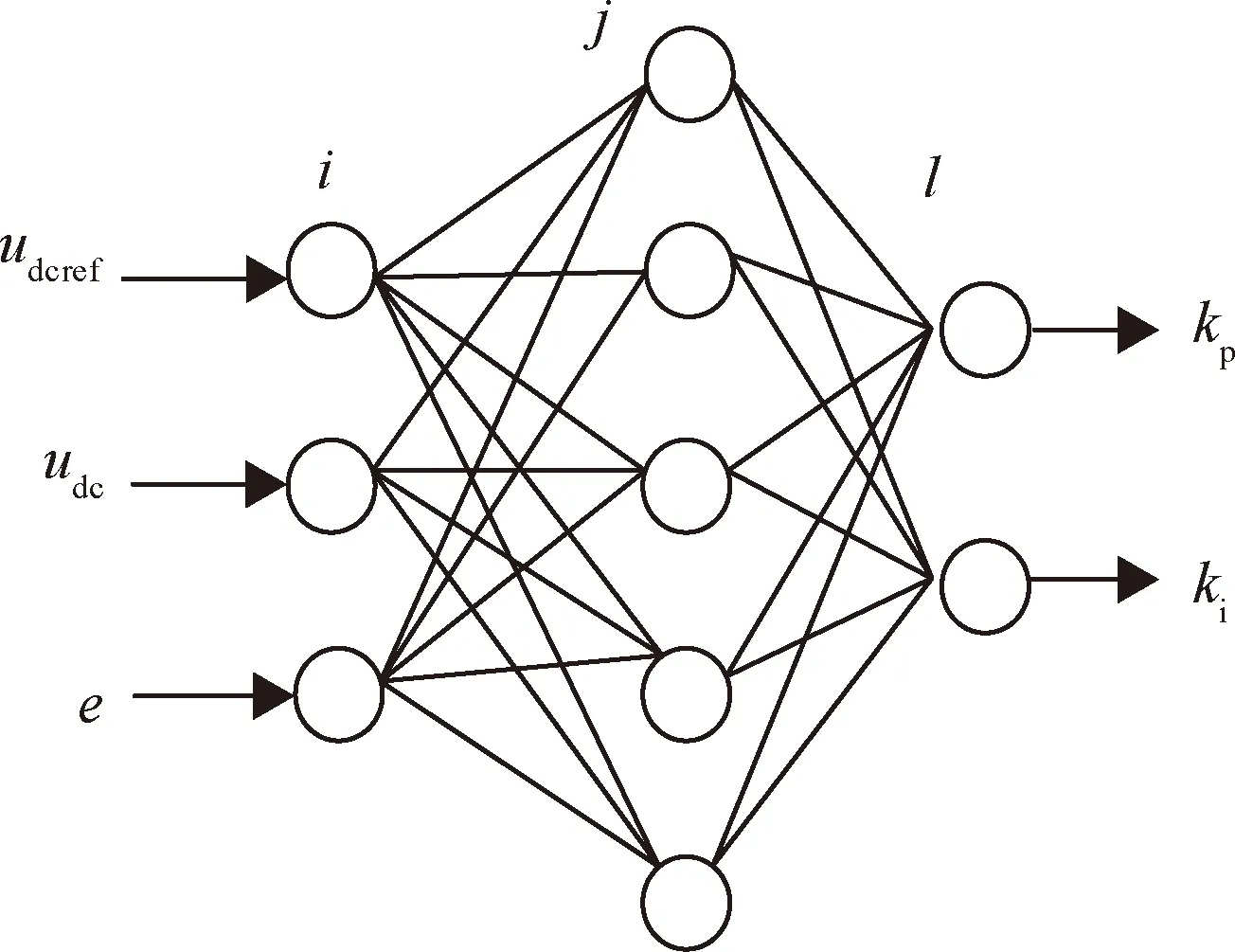
图2 BP神经网络结构

设补偿的电流值为Δidref，则BP神经网络优化的PI控制器为

u(k)=u(k-1)+kp(e(k)-

e(k-1))+kie(k)

(16)

式中的u(k)为控制量Δidref。

原内环PBC的电流得到补偿后为

隐含层的输入输出为

(17)

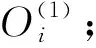
隐含层的激励函数：

(18)

输出层输入、输出函数为

(19)

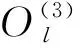
kp、ki为非负，输出层激励函数选取：

(20)

输出层的输出为PI的两个参数：

(21)

均方误差函数定义为

(22)

采用最速下降法沿负梯度方向对加权系数进行调整，使得E(k)最小时能够得到权值矩阵最优值，输出层的梯度式为：

(23)

其中：

(24)

(25)

由式(16)、(21)可得

(26)

则：

(27)

由式(19)可得：

(28)

(29)

则式(23)可写成：

(30)

其中

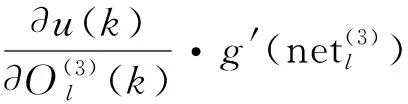
(31)

权值变化量与误差函数成正比，为加快误差函数收敛，加入惯性项，则输出层权值更新算法为：

(32)

式中：η为学习率；α为惯性系数。

同理，隐含层权值更新算法为

(33)

其中：

3 实验结果与分析

本文所提BP优化PI+PBC策略的系统结构如图3所示，在Matlab/Simulink中分别采用传统PI双闭环控制以及本文策略对该系统进行仿真，分析比较这两种控制策略的电流谐波。选取BP神经网络算法的学习率为η=0.25，惯性系数α=0.05，采样周期为0.001 s。该变换器的主要参数如表1所示。

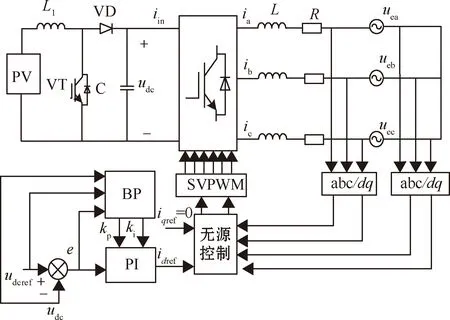
图3 系统控制框图

表1 变换器参数

注入不同大小的阻尼Ra会对系统的动态响应产生不同的影响，对于不同的阻尼参数，逆变器输出的d轴的电流波形如图4所示。可以看出Ra>20 Ω以后的波形与Ra=20 Ω基本接近，说明系统的动态响应基本不会再发生变化，因此本文最终选取阻尼参数为20对系统进行仿真。

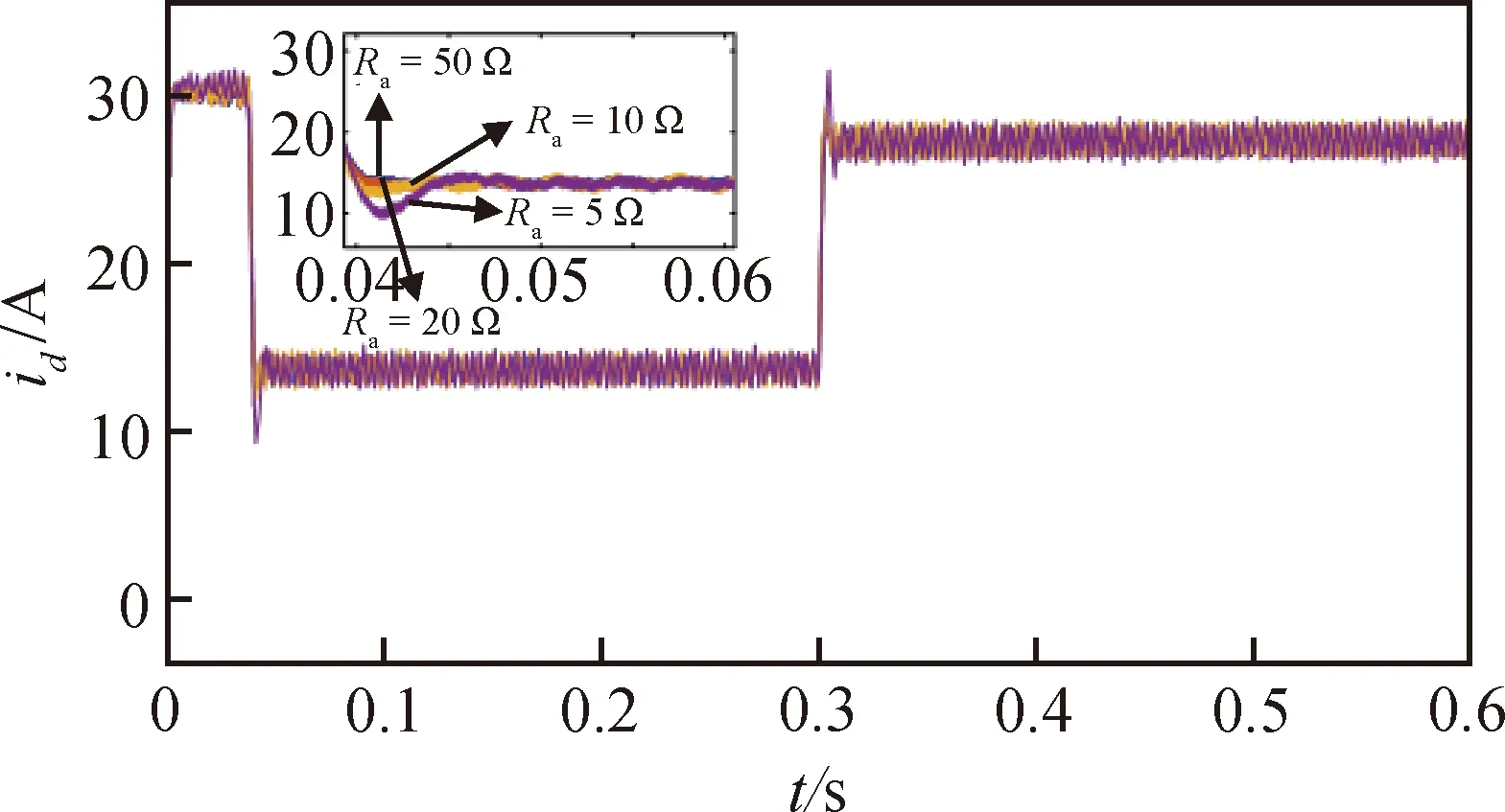
图4 不同Ra时系统动态响应比较

为验证系统的稳态性能，对本文控制算法进行仿真。该控制算法下的d轴电流跟踪误差以及a相并网电流、电网电压波形如图5、6所示。可以看出该控制策略下的电流跟踪误差能迅速趋于零，实现并网电流与电网电压同相，且能稳定跟踪期望值，说明在BP优化PI+PBC策略下，电流能够实现无差跟踪，具有良好的稳态性能。

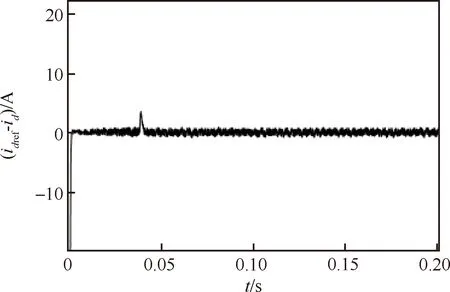
图5 电流跟踪误差

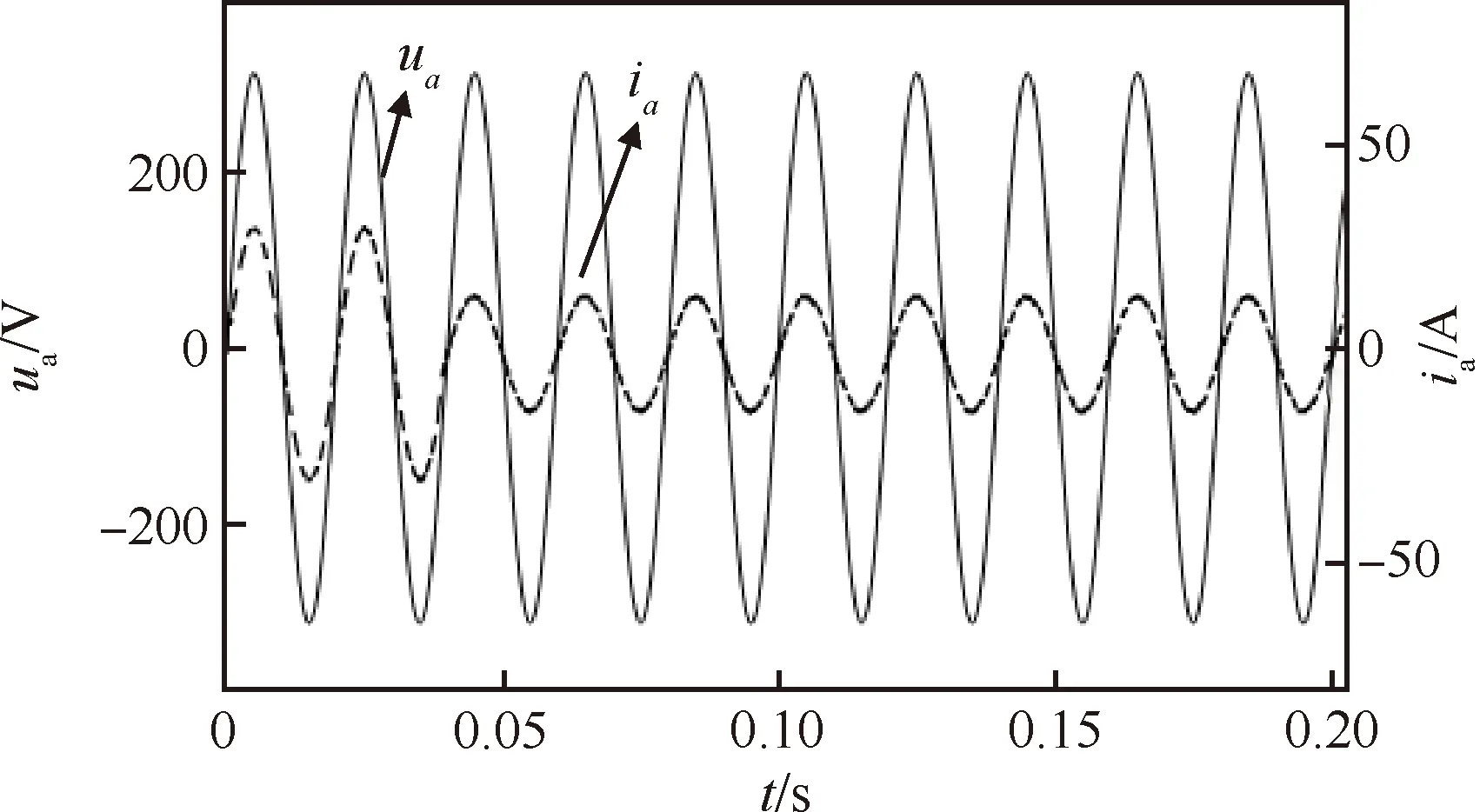
图6 a相并网电流、电网电压

为验证所提控制策略的动态性能，在0.3 s时模拟负载发生跳变，采用BP优化的PI+PBC进行仿真，其三相电流如图7所示。从图中可以看出该控制策略下的电流跟踪过程快速平稳，具有良好的动态性能。

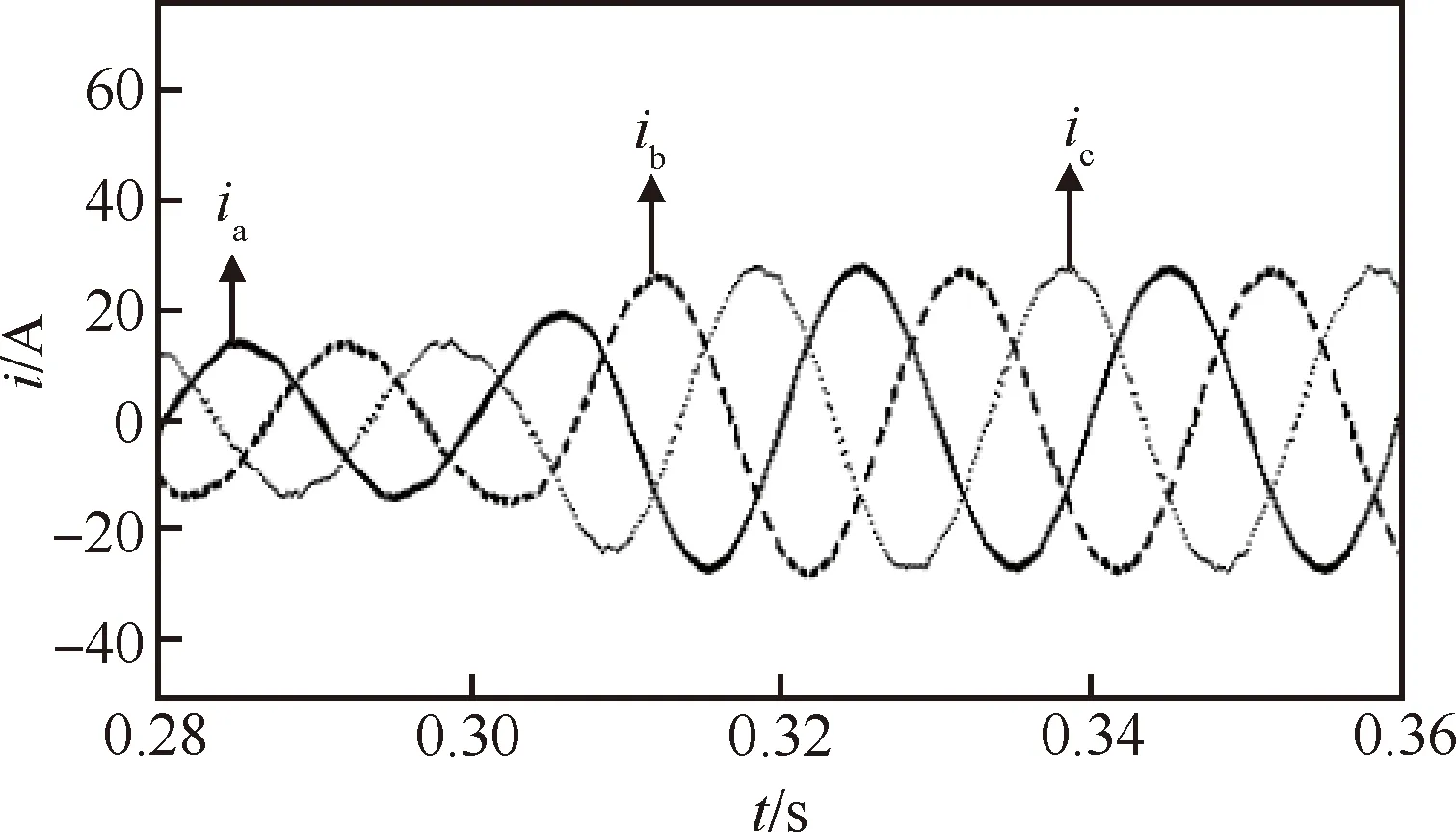
图7 BP优化PI(PBC下的三相电流

采用PI控制以及本文策略下的a相并网电流频谱分别如图8、9所示。入网电流基波幅值分别为13.68A、27.43A，两种控制策略的THD分别为3.79%、1.79%，相较于PI控制，本文BP优化PI+PBC控制策略可有效降低并网电流的谐波，提高入网电流质量。

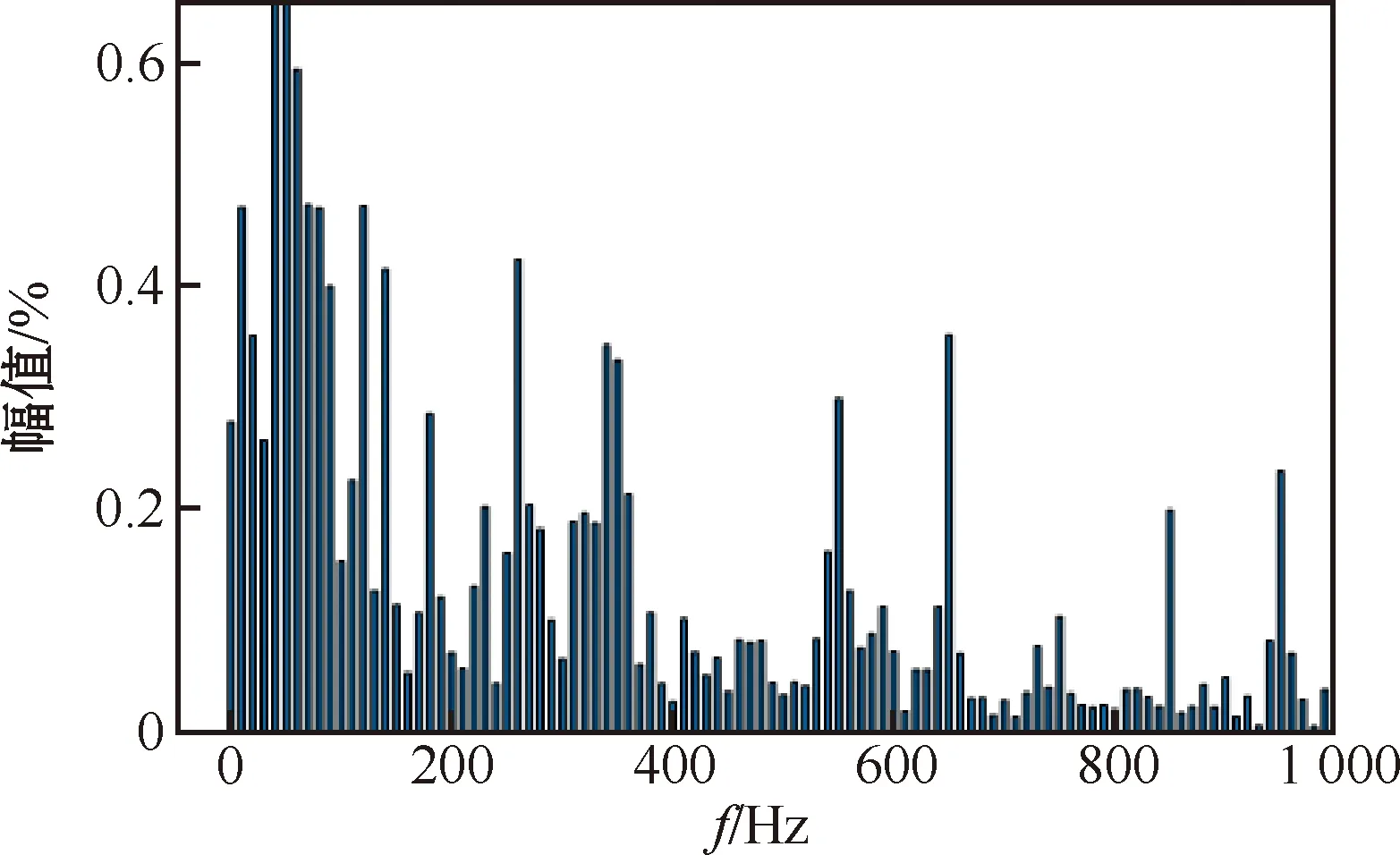
图8 PI双闭环控制下的并网电流谐波

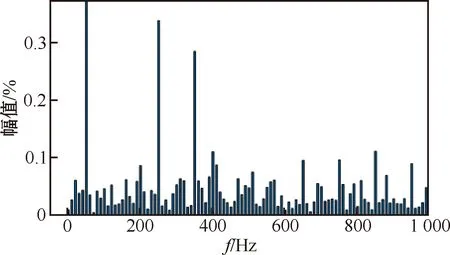
图9 BP优化PI+PBC下的并网电流谐波

4 结束语

本文对三相并网逆变系统，采用阻尼注入的方式建立了基于EL模型的电流内环PBC策略，为解决PBC不能精确趋于稳定点的问题，引入具有惯性项的BP算法优化的PI外环控制器来补偿电流内环精度。其仿真实验结果表明：本文复合控制策略可可消除并网电流稳态误差，实现并网电流无差跟踪，相较于传统PI控制，可有效抑制并网电流谐波，具有良好的控制效果。