基于王石灌区水资源供需时序关系研究
2022-11-23张亮
张 亮
(辽宁省绥中县水利事务服务中心,辽宁 绥中 125205)
灌区灌溉作为农业用水大户,在一定程度上决定了农业生产和区域粮食安全[1]。近年来,灌区农业发展受人类活动、气候条件等因素的影响较大,因无法准确预测灌溉水量,使灌区用水效率明显下降,极大地威胁着灌区用水安全。水资源供需时序的匹配情况直接决定了灌溉用水安全,为有效控制水资源短缺风险以及更加科学地管理灌区,切实保障灌溉用水安全,必须有效识别和评估水资源的供需时序相关性及其系统风险。受下垫面条件、气候变化和人类活动等诸多因素影响,对水资源的供需时序相关性利用常规的方法很难完整精准分析[2-5]。另外,灌区水资源供需时序同其它时间序列一样,表现出显著的多时间尺度特征[6-7]。为尽可能接近实际情况,更加准确地分析有关数据,对水资源供需时序关系利用多时间尺度分解时能够取得较好的成效,更加充分地了解和认识序列的变化趋势及其内在特征,关于水资源供需时序利用多时间尺度分解分析的研究也越来越多[8]。
在较长时期内灌区水资源供需时序的各个要素具有明显的均衡关系,这种关系在短期内并不明显,在描述这种均衡关系时利用传统的回归计算法通常存在“伪回归”的问题,对于t统计量与拟合度而言,该方法能够取得较好的效果,但DW检验值往往处于较低水平。为解决这种非平稳序列的“伪回归”问题,水文水资源领域有关学者提出了协整理论,因考虑了序列的不平稳性这种理论被广泛应用于经济学、水文水资源等领域[9-10]。
葫芦岛市绥中县境内的王石灌区东西长度为36000m,南北宽度为29000m,灌区境内耕地总面积为26800hm2,灌区设计规划节水面积20800hm2,实际灌溉面积14000 hm2,其中:水田2667hm2、麦田1333hm2、菜田1667 hm2、玉米7333hm2以及其他作物面积1000hm2。灌区渠系工程现有2条长度为53900m的总干渠,254座渠系水工建筑物,已经铺设的灌区衬砌长度7900m;17条干渠总长度为113940m,干渠的建筑物总共有422座,已经铺设的灌区衬砌长度为16880m;57条支渠总长度为114500m,支渠的建筑物总共有1142座,灌区灌溉的水资源有效利用系数为0.58[11-13]。本研究以王石灌区为例,采用非线性协整理论构建作物需水量、灌溉水量与降水量之间的关系,在此基础上进一步探讨了水资源供需时序关系,通过科学预测灌区灌溉水量,旨在为提高灌区用水安全水平和水资源调配能力提供一定支持。
1 非线性协整原理
对于具有长期均衡关系且能够满足同阶单整特点要求的一组时间序列,一般选用线性协整理论进行分析;针对无法满足线性协整关系的一组时间序列,利用线性组合的方法则很难消除序列的协整关系,该条件下可以利用非线性理论进行序列的处理。我国学者深入研究了非线性协整关系,如张喜彬等[14]将神经网络理论引入非线性协整模型,其建模流程为:①引入n维时间序列Xt=(x1t,x2t,…,xnt),则非线性协整就是{Xt}的分量;②若长记忆序列为xit,其中i=1,2,…,n,则存在非线性协整函数f(·)能够使yt=f(x1t,x2t,…,xnt)为短记忆过程;③对于满足线性关系的f(·)函数,则存在以下表达式:
(1)
式中:α=(α1,α2,…,αn)T为RT中的向量,从长期记忆性上{Xt}中分量序列符合单整性要求,非线性协整关系可以用线性关系来描述。因此,可以认为非线性协整属于线性协整的应用范畴。
此外,也有学者将小波神经网络引入非线性误差校正模型,其建模流程为[15]:①分析数据的非线性协整关系,将建模数据序列划分成训练和预测两个集合;通过对分形维数的分析,若训练集数据分形维数互不相等则表明其存在非线性协整关系,数据的分形维数可以利用分数维经验公式和赫斯特指数计算;②确定非线性协整函数{f(·)},在创建非线性协整关系时引入小波神经网络,为保证模型收敛精度,通过修改学习速率、动量因子和隐含层数等方法优化模型;③检验输出序列,对小波神经网络输出序列利用非线性协整模型进行检验,赫斯特指数在0.5以下时则代表序列的非线性协整关系良好;④建立误差校正方程,将训练集序列和非线性协整函数{f(·)}利用差分方法进行处理,向非线性误差校正方程输入训练集处理后的数据;⑤预测分析,对预测集序列利用差分方法进行处理,并向步骤4中的非线性误差校正方程输入预测集处理后的数据,从而输出预测结果,并进一步分析预测精度。
2 水资源供需时序关系
为了科学预测分析水资源供需时序,必须考虑各种因素对灌区作物需水量的影响,全面掌握作物腾发量、降雨量与灌溉水量之间的关系,本研究选择作物需水量ETc和灌区降雨量P为自变量,灌溉水量IR为因变量,从而建立非线性协整模型和BP神经网络模型,并对比两种模型的预测精度,进一步研究各要素的非线性协整关系。
2.1 多时间尺度BP网络训练
采用BP网络模型研究分析3个变量,以1976-2009年数据为训练集,2010-2019年数据为预测集,设定输入层节点12个,输出层节点1个,目标精度0.01。经学习训练,训练集均方误差最小时所对应的最大迭代次数为1600,隐含层节点10个,学习速率0.86,可以达到迭代收敛精度要求,BP网络训练过程曲线,见图1。
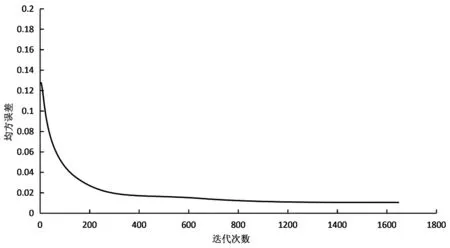
图1 BP网络训练过程曲线
由图1可知,迭代次数达到1260次时均方误差趋于稳定,最终收敛值为0.012,虽然较目标精度0.01存在一定差异,但整体拟合效果良好。然后利用训练好的模型和预测集,对降雨量进行预测,实际和预测降雨量以及两者的误差,BP网络的预测灌溉雨,见表1。
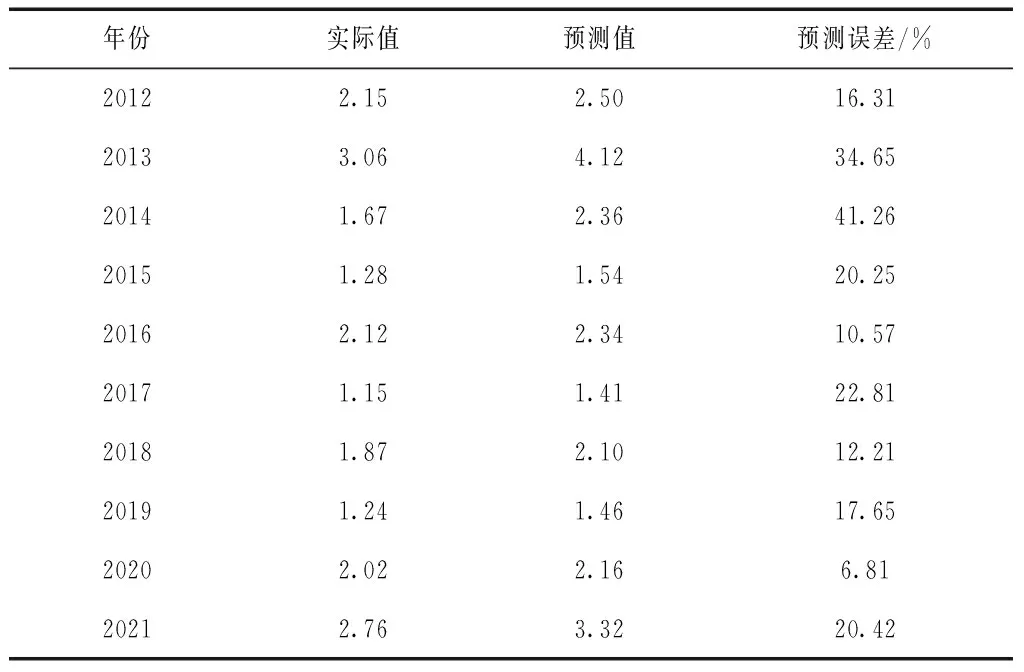
表1 BP网络的预测灌溉雨量
由表1可知,2014年BP网络预测的降雨量量误差最大为41.26%,2018年BP网络预测的灌溉水量误差最小为6.81%,预测误差整体较大,10a平均误差达到20.2%。
2.2 原始序列非线性协整分析
以降水量P和作物需水量ETc的原始序列为自变量,以灌溉水量IR的原始序列为因变量,原始序列非线性协整分析时的赫斯特指数H,原始序列赫斯特指数H的计算值,见表2。

表2 原始序列赫斯特指数H的计算值
由表2可知,降水量P和作物需水量ETc的原始序列赫斯特指数非常接近,表明在短记忆方面这两个序列的相似性比较显著,究其原因是P通过直接观测获取而ETc按气象要素来确定,因此具有较高的相似性。
采用公式D=2-H计算原始序列的分形维数D,原始序列分形维数D的计算值,见表3,结果显示作物需水量与降雨量的分形维数非常接近,由此表明两者之间呈现出显著的非线性协整关系。
入口导叶开度用来调节压缩机进出口压力和循环气流量,满足工艺生产的需要,同时保证压缩机工作在稳定的工作区内。为防止过载,该控制采用出口压力与主电机电流超弛控制,低选后控制入口导叶。

表3 原始序列分形维数D的计算值
3个变量的滞后阶数利用Eviews软件计算,其结果为2。将34组数据差分值和BP网络训练集的参数值输入非线性误差校正方程,并对非线性协整方程系数利用Eviews软件进行计算,具体表达式为:
ITt=28.5×ETct-1×20.05×Pt-1
-1.56×YNN+25.380
(2)
式中:Pt-1、ETct-1为作物需水量和降雨量的一阶差分,t-1代表第t-1位置;YNN为变量的非线性函数。
一阶差分处理2012-2021年王石灌区灌溉水量、降水量和作物需水量原始序列数据,并向非线性误差校正方程输入差分后的数据,从而获取非线性协整模型预测的灌溉水量误差,非线性协整模型预测的灌溉水量,见表4。
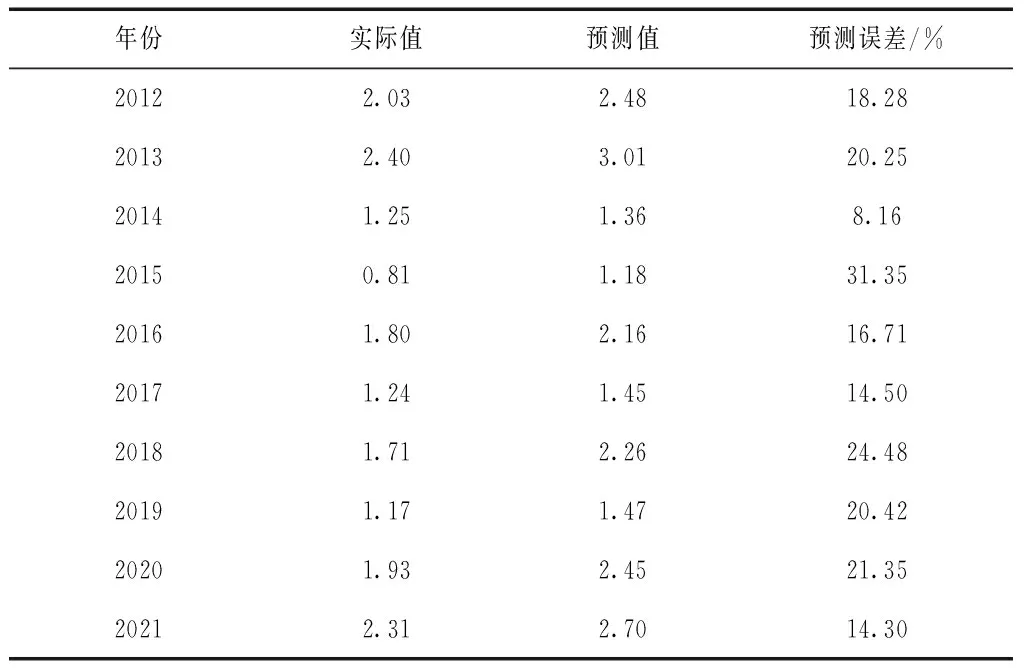
表4 非线性协整模型预测的灌溉水量
由表4可知,2015年非线性协整模型预测的灌溉水量误差最大为31.35%,2014年该模型预测的灌溉水量误差最小为8.16%,预测误差整体较高,10a平均误差达到19.0%。
2.3 多时间尺度非线性协整预测
根据前文所述流程,多时间尺度非线性协整预测该灌区灌溉水量、降水量和作物需水量3个变量,格斯特指数计算结果,多时间尺度赫斯特指数H的计算值,见表5。
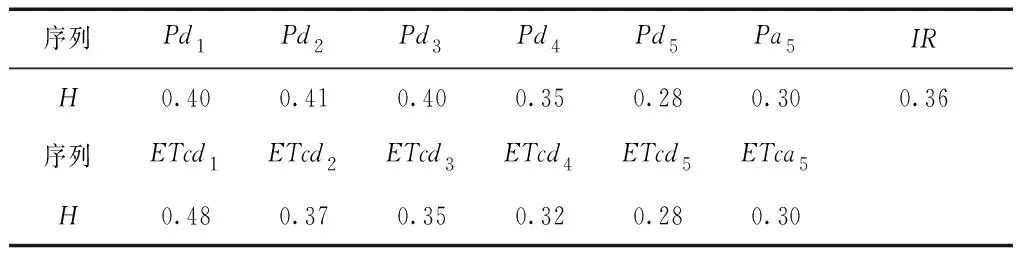
表5 多时间尺度赫斯特指数H的计算值
采用表5中的数据和公式(2),可以计算多时间尺度作物需水量和降雨量序列的分形维数,多时间尺度分形维数D的计算值,见表6。
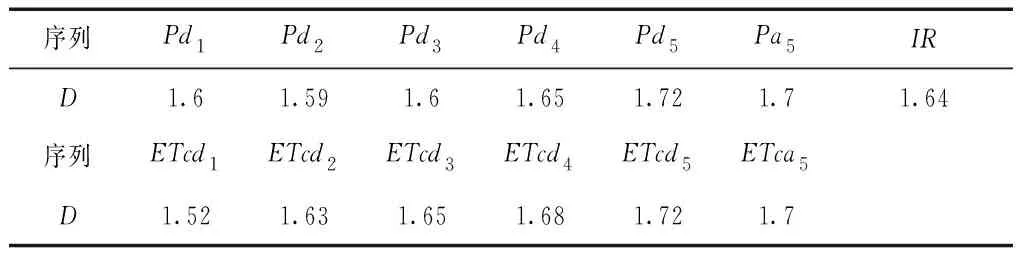
表6 多时间尺度分形维数D的计算值
由表6可知,灌区作物需水量、降雨量原始序列的分形维数与灌溉水量存在明显差异,说明三个变量的非线性协整关系比较显著。采用小波神经网络拟合分析1976-2009年3个变量的非线性协整关系,输入节点数12个,输出节点数1个,为最大程度地减小训练集均方误差,测试过程中设定学习速率0.06,动量因子0.2,隐含层数6个,小波神经网络训练过程曲线,见图2。
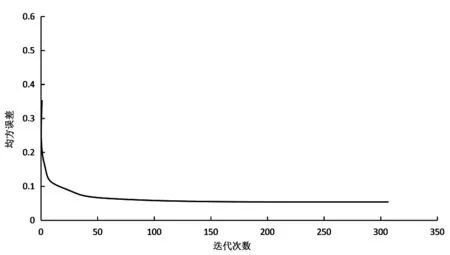
图2 小波神经网络训练过程曲线
由图2可知,迭代次数达到100次时均方误差趋于稳定,最终收敛值为0.075,模型整体拟合效果良好。然后利用训练好的模型和预测集,对灌溉水量进行预测,实际和预测灌溉水量以及两者的误差,小波神经网络的预测灌溉水量,见表7。

表7 小波神经网络的预测灌溉水量

续表7 小波神经网络的预测灌溉水量
经计算,序列赫斯特指数0.41满足<0.50的要求,故预测序列存在非线性协整关系。然后对三个变量的滞后阶数利用Eviews软件计算,其结果为2。将34组数据差分值和小波神经网络训练集的参数值输入非线性误差校正方程,并对非线性协整方程系数利用Eviews软件进行计算。
一阶差分处理2012-2021年王石灌区灌溉水量、降水量和作物需水量多时间尺度原始序列数据,并向非线性误差校正方程输入差分后的数据,从而获取非线性协整模型预测的灌溉水量误差,多时间尺度非线性协整模型预测结果,见表8。

表8 多时间尺度非线性协整模型预测结果
由表4可知,2013年多时间尺度非线性协整模型预测的灌溉水量、作物需水量和降水量误差最大为12.25%,2018年该模型预测的灌溉水量、作物需水量和降水量误差最小为0.28%,预测误差整体较小,10a平均误差达到6.8%,能够满足预测精度要求。
2.4 讨论分析
文章利用非线性协整理论检验了1978-2021年王石灌区的降雨量、作物需水量和灌溉水量之间的非线性协整关系,通过非线性协整模型验证了三个变量之间的非线性协整关系,可利用非线性协整误差校正方程量化分析灌区水资源供需关系。
经分析:在多时间尺度分解的灌区降雨量、作物需水量结果中趋势项Pa5和ETca5对应的系数值最大,相关性与政府性分析结果一致,高频项系数小而低频项系数达,表明趋势项式多时间尺度分解中占主导作用的项。
采用误差分析法对原始序列非线性协整模型、多时间尺度BP网络模型和多时间尺度非线性协整模型进行对比,结果显示能够达到序列预测精度的是非线性协整模型,多时间尺度非线性协整模型对突变点预测具有明显的优势,协整理论对波动修正“拉回”时表现突出。
3 结 论
以王石灌区为例,对灌区水资源供需时序关系利用非线性协整理论进行分析,并将分析结果与BP网络预测值对比,结论如下:
1)1978-2021年王石灌区降雨量、作物需水量与灌溉水量之间存在非线性协整关系,可以利用非线性协整模型研究灌区水资源供需时序。
2)对比分析10a预测值和实际值,结果显示多时间非线性协整模型的整体误差较小,预测精度较高,预测效果整体较好,协整理论对波动修正“拉回”时表现突出,而多时间尺度BP模型的整体误差较大,预测精度较低。
