空间弯管的几何计算
2022-11-23张发茂杨宗儒
张发茂,杨宗儒
(中水珠江规划勘测设计有限公司,广州 510610)
0 引 言
在水利工程中布置管道时,管轴线尽可能采用直线布置,但由于受地形、空间和水工布置等因素的制约,不可能完全采用直线布置。弯管的布置不可避免,在垂直平面或水平面内转折的钢管为平面弯管,其几何尺寸在垂直平面和水平面的正投影即为管轴线的实际长度,计算较为简单,文章重点介绍同时在垂直方向和水平方向弯曲的空间弯管几何尺寸的计算方法。
1 弯管一般计算方法
空间弯管是指在水平面和垂直平面都有弯折的钢管,在空间不受限的情况下,可采用两个平面弯管构造,在空间狭小或对水头损失敏感的部位,就有必要采用一个空间弯管代替两个不同平面的弯管。空间弯管由于其在垂直面和水平面正投影均不能反应其真实的管轴线长度,故须通过找到两条空间转折线确定的唯一平面,在这个平面上投影才能真实反应空间折线的长度和角度[1]。
1.1 空间弯管转折角计算
由钢管轴线的几何关系可知,相交于一点的两条直线可确定一个平面,故空间管的空间曲线仍为平面曲线,只是该平面为一倾斜面。如图1,OA’、OB’相交于O点。
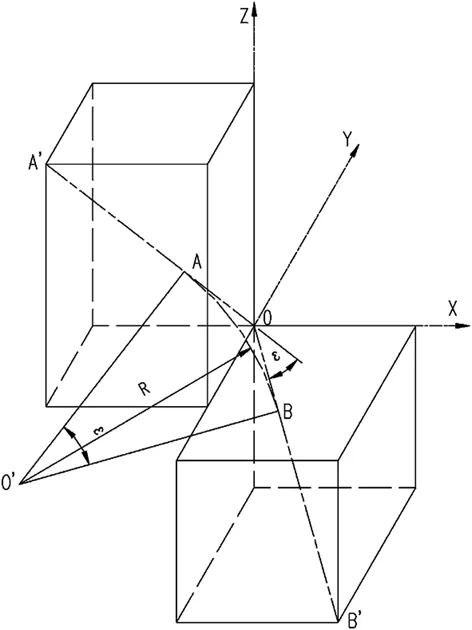
图1 空间弯管曲线平面图
设定转折点O为坐标原点:O(xo,yo,zo)即O(0,0,0)
已知空间直线OA’(xA′,yA′,zA′)和空间直线OB′(xB′,yB′,zB′)

ε=cos-1
上述已计算出管轴线的转折角ε,角度ε等于弯管的转弯角度,按照角度ε制造出的弯管即A‘OB‘平面内的弯管。
1.2 转弯切点的确定
管轴线的转折角计算出来后,弯管的转弯角度就确定了,为了确定管轴线转折点之间的钢管直段的实际长度,所以在几何尺寸计算时,还应该把弯管的轮廓尺寸确定下来。水利工程钢管通常为卷制管节再组合焊接成弯管,焊接后的钢管管壁要平顺,水流阻力和水头损失要小等因素。故管轴线坡度不宜过陡,水平转弯不宜过急,转弯角度一般小于90°,最小转弯半径一般采用钢管直径的3倍较为合适,转弯半径大,可减少阻力和水头损失,但施工安装工作量大,相应镇墩体积也大,转弯半径过小则弯管管壁不易做得平顺,水流阻力和水头损失较大[2]。

根据以上计算即可设计出AOB平面内弯管的切点坐标。
切点A坐标:
切点B坐标:
1.3 安装角计算
弯管安装到空间位置时,弯管自身的平面和它的中心轴线与管轴线上的坐标轴是不重合的,它们之间相差的角度就是空间弯管的安装转角。安装角在上游端管口和下游段管口的角度是不同的,为了安装的方便时,不仅要知道弯管切点A、B的坐标,还需要知道通过A、B点与钢管轴线正交的平面,以及弯段如何倾斜,向那一方向安装,故还须计算弯管上、下切口的安装角。
1.3.1 上切口安装角计算[1]
空间弯管AOB所在平面的法向量。
过原点O(0,0,0)AOB平面的点法式方程,记作平面AOB:
il·x+jl·y+kl·z=0
过切点A(xA,yA,zA)垂直于直线OA平面的法向量:m=(xA,yA,zA)
⊥直线OA且过A点的平面点法式方程,记作平面⊥OA:
xA·(x-xA)+yA·(y-yA)+zA·(z-zA)=0
过切点A,A(xA,yA,zA)水平面的法向量:n=(0,0,1)
水平面的点法式方程,记作水平面A:z=zA
上切口安装角:
1.3.2 下切口安装角计算
与上切口安装角计算类似。
过原点O(0,0,0)AOB平面的点法式方程,记作平面AOB见上切口安装角计算:
过切点B点(xB,yB,zB)垂直于直线OB平面的点法向量:r=(xB,yB,zB)
⊥直线OB且过B点的平面点法式方程,记作平面⊥OB:
xB·(x-xB)+yB·(y-yB)+zB·(z-zB)=0
过切点B,B(xB,yB,zB)水平面的点法向量:s=(0,0,1)
水平面的点法式方程,记作水平面B:z=zB
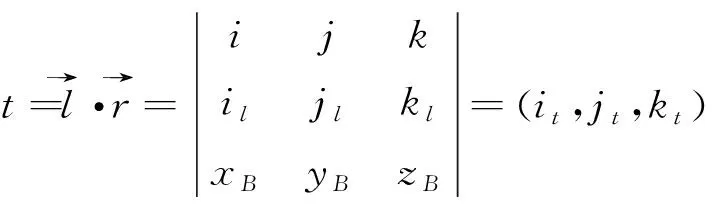
下切口安装角:
1.4 圆心坐标计算
平面AOB、平面⊥OA和平面⊥OB的交点即为圆心,联列3个平面方程:
求解即得出圆心坐标,O′(x′o′,y′o,z′o)。
通过将圆心坐标O’(x′o′,y′o,z′o)与A(xA,yA,zA)、B(xB,yB,zB)两点分别求距,得出二者距离均等于转弯半径,可进一步验证计算结果,见下式。
1.5 计算算例
以转折点O为坐标原点,已知点A′和B′的坐标分别为A′(-40,-30,15),B′(50,-20,-10),钢管转弯半径R=12m,计算弯管的几何参数。
1.5.1 转折角计算
按照上述推导公式可进行空间弯管的计算,管轴线的转折角ε。

ε=57.173°
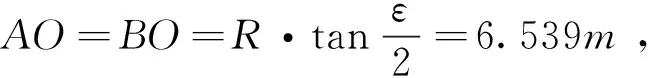
1.5.2 上切口安装角计算
空间弯管AOB所在平面的法向量:

(8.973,5.234,34.395)
过原点O(0,0,0)AOB的点法式方程,平面AOB:
8.973·x+5.234·y+34.395·z=0
过切点A垂直于直线OA平面的法向量:m=(-5.01,-3.758,1.879)
⊥直线OA且过A点的平面点法式方程,平面⊥OA:
(-5.01)·(x+5.01)+(-3.758)·(y+3.758)+1.879·(z-1.879)=0
过切点A,A(-5.01,-3.758,1.879)水平面的法向量:n=(0,0,1)
水平面的点法式方程,水平面A:z=1.879
平面AOB与平面⊥OA交线的方向数:

平面⊥OA与水平面A交线的方向数:

1.5.3 上切口安装角

φs=1.908°
1.5.4 下切口安装角计算
过切点B垂直于直线OB平面的点法向量:r=(5.969,-2.388,-1.194)
⊥直线OB且过B点的平面点法式方程,平面⊥OB:
5.969·(x-5.969)+(-2.388)·(y+2.388)+(-1.194)·(z+1.194)=0
过切点B,B(5.969,-2.388,-1.194)水平面的点法向量:s=(0,0,1)
水平面的点法式方程,水平面B:z=-1.194
平面AOB与平面⊥OB交线的方向数:
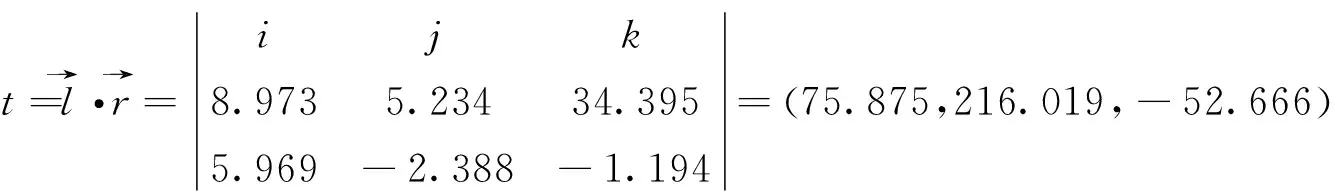
平面⊥OB与水平面B交线的方向数:
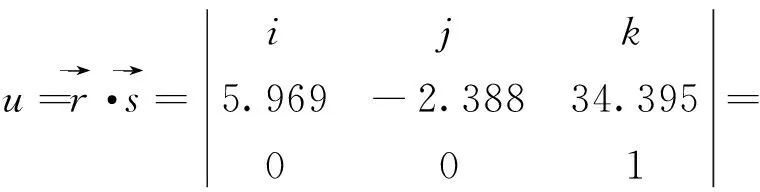
下切口安装角:

1.5.5 圆心坐标计算
平面AOB、平面⊥OA和平面⊥OB的交点即为圆心,联列三个平面方程:
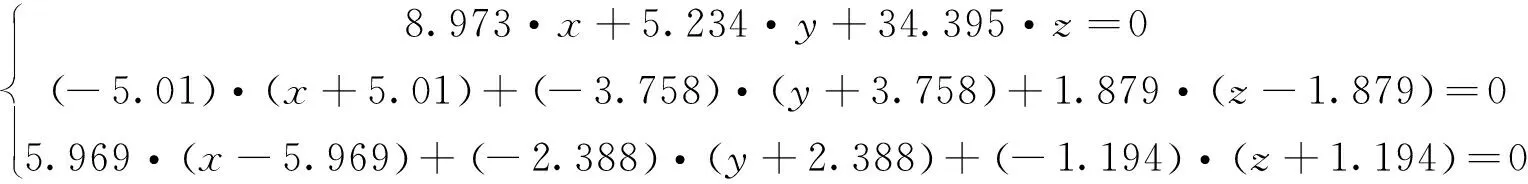
求解即得出圆心坐标,O’(2.094,-13.421,1.496)。

2 线路工程简化计算
在供水线路工程中,管轴线坐标随管线走向变化,以其中一个转折点为例,可将钢管转折点前段轴线置于XOZ平面,令yA'=0,可知转折点前段直线OA’(xA',0,zA'),转折点后段直线OB’(xB',yB',zB'),如图2所示。
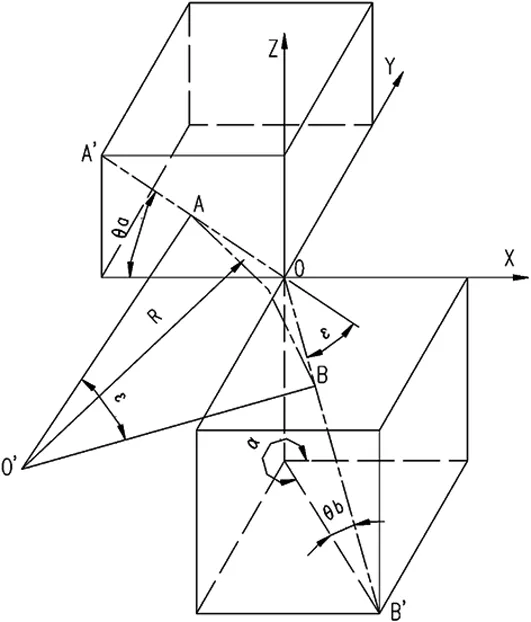
图2 空间弯管几何计算图
根据上述计算过程介绍,空间弯管几何计算过程已经明确,根据其坐标系,则有:
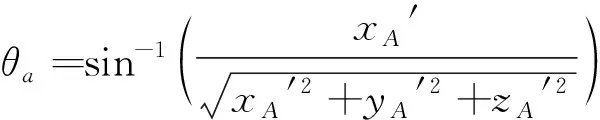




直线OA′与OB’在AOB平面内的夹角ε满足下式:
ε=cos-1(-cosθa·cosθb·cosα+sinθa·sinθb)
在线路工程中,θa、θb和α角一般为已知角度,故计算可大大简化。确定转弯角度后,切点坐标、上下切口安装角及圆心坐标计算同第二节,在此不在赘述。
3 结 语
空间弯管各参数计算工作量较大,通过上述公式推导后结合计算软件,可将其计算参数化,简化计算过程,简化后可快速计算出弯管平面转折角、上下切口安装角和圆心等参数,在工程设计中可有效提高计算效率[3]。
