提篮式型钢悬挑脚手架受力机理分析

2022-11-23耿大将龙敏健金学胜苗恩新柏志诚

粘接 2022年11期

耿大将，龙敏健，金学胜，苗恩新，柏志诚

(1.中建四局第六建设有限公司，上海 201100； 2.中国建筑第四工程局有限公司，上海 201100)

脚手架在建筑结构施工，尤其是住宅建筑施工中具有十分重要的作用。按照作用原理的不同，建筑脚手架目前主要包括附着式升降架、爬架和悬挑架等形式[1-4]。悬挑架根据其受力体系的不同可以分为完全悬挑式、下撑悬挑式、上拉悬挑式及下撑上拉悬挑式[5-7]。有学者对上拉悬挑式脚手架施工技术进行了探讨，将上拉悬挑式脚手架引入到装配式结构施工、高层建筑施工中[10-12]；对上拉悬挑式脚手架与完全悬挑式脚手架进行了优劣势对比分析[13]；还有的直接给出了上拉悬挑式脚手架的设计方案[14]。综合国内已有的研究结果可以看出，尽管上拉悬挑式脚手架已经在工程中得以应用，但相关的研究工作仍然主要集中在施工技术方面，对该类脚手架受力机理仍然有待进一步的明确。只有在明确其受力机理，才能进行更好地脚手架设计工作，从而保证实际施工过程中脚手架的使用安全。

为了明确提篮式脚手架的受力机理，本文对提篮式脚手架进行了构造分析，明确了其主要受力构件体系；然后对主要受力构件体系进行了现场原位加载试验，试验结果验证了有限元分析方法在提篮式脚手架受力机理分析方面的有效性。最后采用多变量分析法对提篮式脚手架受力机理展开分析。

1 提篮式型钢悬挑脚手架构造分析

如图1(a)所示，传统悬挑脚手架的悬挑主梁需要穿过墙体进入楼地面，然后与楼地面通过螺栓固接，悬挑主梁为其主要受力构件；如图1(b)、(c)所示的提篮式型钢悬挑脚手架，其型钢主梁不需要穿越墙体，而是直接通过螺栓固结于结构梁边或墙边；此外，型钢主梁还与1根或2根拉杆相连，拉杆上端同样通过螺栓与建筑结构相连。无论对于传统悬挑脚手架还是提篮式型钢悬挑脚手架，其传力路径均为脚手板→纵向水平杆→横向水平杆→立杆→型钢主梁，不同的是传统悬挑脚手架会将力直接传递给楼板；提篮式型钢悬挑脚手架会将型钢主梁受力部分传递给拉杆，最终通过型钢主梁和拉杆传递给建筑结构。由此可看出，提篮式型钢悬挑脚手架的主要承载结构为型钢主梁和拉杆组成的体系，这也是其与传统悬挑脚手架最大的不同。因此，需要对该承载体系进行受力性能分析，以更好地指导工程实践。

(a)传统悬挑脚手架

2 现场原位试验

2.1 原位试验概况

为了明确提篮式型钢悬挑脚手架主要承载体系的受力性能，同时验证后续所采用的有限元分析方法的有效性，进行了如图2所示的原位加载试验。在建筑施工现场建立了如图2(a)所示的试验系统，该系统主要包括：如图2(b)所示的数显式千斤顶加载系统、如图2(c)所示的靠墙端部的主梁上翼缘应变监测和如图2(d)所示的主梁下翼缘挠度监测系统。

本试验主梁采用长1.4 m的18号工字钢和直径22 mm的拉杆，拉杆与主梁连接点与主梁固接端的距离为105 cm。在主梁的2端和中部位置共设置了3个挠度监测点，距主梁固接点的距离分别为20.5、71.0和119.0 cm；主梁的上翼缘轴向应变监测点位于主梁固接点处，主梁固接点与拉杆上拉结点的竖向距离为3.0 m。

二加载点距主梁固接点的距离分别为38.0、118.0 cm，试验尽可能模拟实际施工过程。内外加载点施加相同的集中力，采用分级加载模式，分别加载5.0、10.0、15.0、20.0、25.0和30.0 kN。如图2(e)所示，每级加载稳定后读取3个挠度数据和1个应变数据并做记录。

(a)整体试验系统

2.2 试验结果分析

各级加载下的试验结果如表1所示。

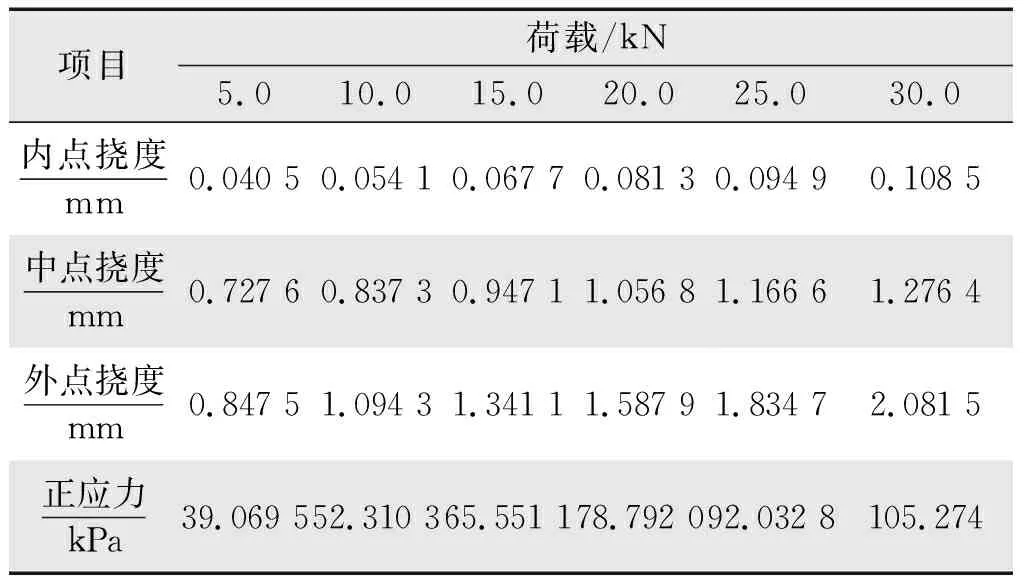
表1 各级加载下的试验结果Tab.1 Test results under various levels of loading

由表1可知，随着荷载呈等差数列式增加，内点挠度、中点挠度、外点挠度和正应力均呈等差数列式增加；表明整个加载过程中主梁和拉杆组成的体系一直处于线弹性工作状态。

3 有限元多变量分析

3.1 有限元方法的有效性验证

有限元计算方法是一种十分重要的现代数值计算方法，在工程实际中应用广泛[15-16]。与原位试验相比，具有实施成本低、获得信息全面、便于多变量分析的优点；但在采用有限元分析方法之前必须先保证该方法对所分析问题的有效性。采用有限元分析方法对拉杆与主梁结构体系进行受力分析，几何尺寸、加载程序、位移监测点、应力监测点均与原位试验相一致。在有限元计算中，主梁一端完全固定、一端自由，采用2节点线性梁单元。拉杆上节点采用铰接模式，拉杆采用2节点线性三维杆单元；主梁和拉杆均采用理想弹塑性本构模型，弹性模量为206 GPa，泊松比为0.30，屈服应力为235 MPa。计算所得结果，以及现场原位试验方法所得挠度和应力、有限元计算方法所得挠度和应力的结果对比均如图3所示。

(a) 内点挠度

由图3可知，除内点挠度外，对中点挠度、外点挠度和正应力，现场试验得出的结果曲线基本平行于有限元法得出的结果曲线。这主要是因为在试验现场拉杆安装时没有与主梁实现完全拉结，导致第1步加载的5 kN荷载中有一部分由主梁完全承担，直到加载荷载较大时主梁和拉杆才开始共同承担荷载。因此，在去除初始拉杆不发挥作用的阶段后，与原位试验结果对比，有限元计算方法在揭示提篮式型钢悬挑脚手架主要承载体系的受力性能方面是可靠的，可用于后续的多变量分析受力机理探讨工作中。此外，建议在具体施工过程中，为了保证拉杆在脚手架初始受力阶段即发挥作用，建议可以在拉杆安装完毕后对其施加一较小(如0.1 kN)的预拉力。

3.2 多变量分析

与传统脚手架相比，提篮式型钢悬挑脚手架设计中最关键在拉杆和型钢主梁组成的承载体系部分。在层高一定的情况下，只要确定了拉杆型号、型钢型号、拉杆与型钢主梁拉结点的位置，即可以完全确定该承载体系；如图1(b)和图1(c)所示，工程实际中常用的有单拉杆和双拉杆2种形式，考虑到单拉杆为双拉杆的内拉杆截面面积为零的特例，因此主要以双拉杆情况为主进行分析。

2拉杆与主梁拉结点的位置均会对斜拉式型钢悬挑脚手架的受力性能产生影响。此外，悬挑主梁所采用的工字钢规格、拉杆规格也均会对脚手架的受力性能产生影响。为明确这些变量对受力性能的影响，采用单因子变量法进行分析，所采用的变量及取值如表2所示；除了需要变化的变量外，其余变量均取图4所示的值。

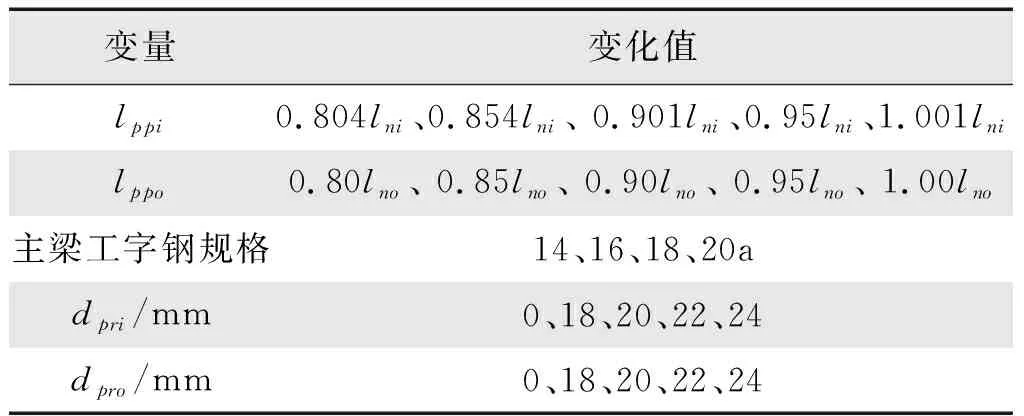
表2 变量取值表Tab.2 Variable value table

由表2可知，lppi和lppo分别表示内拉杆和外拉杆与主梁连接节点距主梁固接点的水平距离；lni和lno分别表示内外集中荷载Fn作用点距主梁固接点的水平距离；dpri和dpro分别表示内拉杆和外拉杆的横截面圆直径。当dpri=0.00 mm时，表示内拉杆失效，只有外拉杆发挥作用；当dpro=0.00 mm时，表示外拉杆失效，只有内拉杆发挥作用。

由图4可知，h表示拉杆上部节点和主梁固接点的竖向距离，取值为3.00 m；lb表示主梁的长度，取值为2.10 m；悬挑主梁主要承受立杆传递的集中荷载Fn=10.14 kN和自重均布荷载q=0.246 2 kN/m。

3.2.1dppi影响分析

图4 计算模型Fig.4 Computational model

不同内拉杆与主梁拉结位置下，主梁内力计算结果如表3所示。

表3 不同拉杆与主梁拉结点位置计算结果对比Tab.3 Comparison of calculation results of different pull rod and main beam tie point positions

由表3可知，My表示主梁的弯矩；Vz表示主梁剪力；wmax表示主梁位于自由端的最大挠度。随着拉结点位置远离主梁固接端，主梁的内力基本不变；而挠度会逐渐小幅减小。这主要是因为在2拉杆同时存在的情况下，外拉杆发挥作用远大于内拉杆；因此，在外拉杆存在的情况下，调整内拉杆拉结点位置不会对主梁受力和变形产生较大影响。在实际情况允许时，建议可以考虑使内拉杆与主梁拉结位置尽可能靠近内立杆位置。

3.2.2lppo影响分析

由表3可以看出，随着拉结点位置远离主梁固接端，主梁的内力和挠度均会逐渐减小，而且减小幅度比变化内拉杆与主梁拉结位置时的减小幅度更大；这是因为外拉杆比内拉杆发挥着更大的拉结作用。建议可以在工程设计和安装工作中使拉杆位置尽可能靠近临近的立杆位置。

对比表3中不同内拉杆与主梁拉结位置、外拉杆与主梁拉结位置下的主梁内力和挠度结果可以看出，主梁内力和挠度受外拉杆与主梁拉结位置的影响更大。可以推断出，外拉杆比内拉杆发挥着更大的作用。

3.2.3主梁工字钢规格影响分析

主梁工字钢规格对主梁内力的影响如图5所示。

(a) 弯矩My

随着主梁工字钢规格尺寸逐渐变大，其内力会逐渐增大；但其挠度会逐渐减小，2拉杆的作用会逐渐减弱即拉杆轴力逐渐降低。因此，建议在实际设计工作中，如果需要有效控制挠度时，可以考虑加大主梁工字钢规格；如果在某些建筑结构部位不便于设置拉杆时，同样可以考虑加大主梁工字钢规格。

3.2.4内拉杆直径dpri影响分析

内拉杆直径dpri对主梁内力、主梁挠度和拉杆内力的影响如表4所示。

由表4可知，随着内拉杆直径的增加，主梁弯矩、主梁挠度和外拉杆拉力均逐渐减小。这是因为内拉杆直径加大，其对主梁的约束能力增强，相应的外拉杆对主梁的约束就会减弱；从而出现主梁挠度和外拉杆拉力均逐渐减小的情况。

3.2.5外拉杆直径dpro影响分析

外拉杆直径dpro对主梁内力、主梁挠度和拉杆内力的影响结果如表4所示。

由表4可知，随着外拉杆直径的增加，主梁弯矩、挠度逐渐减小，而且挠度减小幅度大于内拉杆直径增加时对应的减小幅度，弯矩减小幅度小于内拉杆直径增加时对应的减小幅度。当内拉杆直径为零，即只有外拉杆发挥作用时，主梁弯矩最大为3.802 5 kN·m，主梁挠度最大为1.055 5 mm；当外拉杆直径为零，即只有内拉杆发挥作用时，主梁弯矩最大为3.453 9 kN·m，主梁挠度最大为6.362 9 mm，对比可以看出单独外拉杆作用要大于单独内拉杆作用，即外拉杆作用要强于内拉杆。建议后续设计工作中可以考虑加大外拉杆规格。