考虑光伏波动的有源配电网分布式储能双目标优化规划

招景明，苏洁莹，潘 峰，杨雨瑶，陈明丽，张勇军

（1.广东电网有限责任公司计量中心，广东 广州 510000；2.华南理工大学电力学院，广东广州 510640）

0 引言

目前，构建以可再生能源为主体的新型电力系统是我国的重要战略部署，对未来能源转型、实现2030年“碳达峰”和2060年“碳中和”的目标具有重要作用[1]。分布式可再生能源接入到配用电网络，使配电网有源化、主动化，但大量出力且具有波动性的分布式能源（Distributed Generation，DG）的接入，会造成配用电网络的电压质量恶化、网损增大，影响配电网运行安全性及经济性[2]，[3]。分布式储能（Distributed Energy Storage，DES）具有提高可再生能源消纳率，改善用电网络供电质量，提高经济效益等重要作用[4]，[5]。合理、高效求解DES接入配电网的优化选址与运行策略是亟须解决的问题。

近年来，关于有源配电网DES优化规划的研究受到广泛关注。文献[6]针对DES选址优化求解存在规模较大、速度较慢的问题，采用层次分析法形成储能选址的综合指标建立规划模型。文献[7]基于节点灵敏度分析方法解决了储能选址问题。DG接入配电网后会影响其电压分布，其随机性也会影响不同时刻的电压波动，但现有文献很少考虑不同时刻电压波动与不同运行方式的影响。为了得到合理的储能运行方案，文献[8]从经济性角度进行DES接入配电网的优化规划研究。文献[9]侧重于保证配电网的电能质量进行储能优化配置。现有文献未能综合考虑DES接入对配电网经济性和供电质量的改善。文献[10]运用多目标粒子群算法实现储能规划多目标最优，但易陷入局部最优。文献[11]建立了配电网DES多目标优化配置模型，但选取最优方案时没有考虑主观权重影响，所得方案实用价值较低。

可再生能源出力的不确定性易使储能优化运行方案达不到预期效果，这是求解储能优化策略亟须解决的难题[12]。文献[13]采用鲁棒规划法处理风电的随机波动，以此构建储能优化配置模型，然而鲁棒优化得出的决策方案相对保守。文献[14]利用机会约束规划法研究了含光伏的配电网日前优化调度问题，通过启发式调整机会约束的上下界来求解，但使用机会约束规划法将增加计算工作量和计算时间。场景法可以将不确定性问题转化为多个场景下的确定性问题，降低了问题的难度，能规避分布式能源出力不确定性对储能规划方案的不利影响，具有较强优势[15]。

本文提出了一种考虑光伏波动的DES双目标优化规划方法。首先，采用节点综合灵敏度分析方法考虑配电网电压波动、不同运行状态和运行方式的影响，进行高效的储能布点优化；其次，构建以配电网总成本最小和电压波动总和最小的双目标优化规划模型，利用ε-约束法将双目标问题转化为单目标问题，并以计及主观权值修正的熵权双基点法选取折中最优解。本文基于误差场景模拟计及光伏出力偏离预测值的不确定波动，构建考虑光伏出力随机波动的DES优化规划模型。通过仿真验证所提方法的有效性与适用性。

1 节点电压综合灵敏度分析

为了获得提高配电网运行安全性与经济性的更优效果，亟须以高效的方法确保DES的选址合理性。灵敏度分析方法基于系统当前运行状态量化受扰动场景下系统状态量的变化[16]。节点电压灵敏度能反映节点单位功率变化而引起节点电压的变化程度，以此分析配电网运行未来态。结合灵敏度分析方法选择DES安装位置，能够在改善电压质量的同时，降低DES优化配置的求解规模与提高寻优效率。为反映节点功率变化对节点电压的影响程度，定义节点i的功率变化对任一配电网节点电压影响程度的灵敏度指标Qi，g为

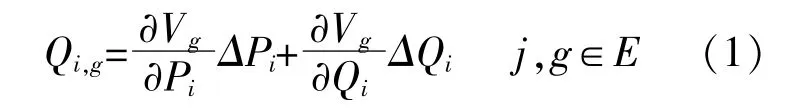
式中：Pi，Qi为节点i的有功功率和无功功率；ΔPi，ΔQi为节点i的有功功率和无功功率的变化量；E为电网节点集合；g为电网节点集合内的任一电网节点；Vg为节点g的节点电压。

一般情况下，DES的接入能有效降低配电网末端节点电压越限风险。然而，分布式光伏接入配电网后影响了配电网电压分布规律，可能同时产生电压偏低和偏高节点。为了从总体上改善配电网电压质量，以增加储能选址的合理性，定义节点i在t时刻的节点电压灵敏度Li，t，综合反映节点i的功率变化对全网节点电压的影响程度。

式中：kg，t为电压偏离程度系数，用于反映配电网节点在时刻t的电压波动程度；Vg，t为节点g在第t时刻的节点电压；Vg，t，ref为节点g的基准电压；Nh，Nl分别为节点电压偏高集合和节点电压偏低集合，均系E的子集。

由于光伏出力与负荷大小的时序变化，配电网在不同时刻的运行状态均不相同，各节点电压灵敏度也会不同。为了进一步考虑不同运行状态对节点电压灵敏度的影响，提出t时刻的影响权重kt为

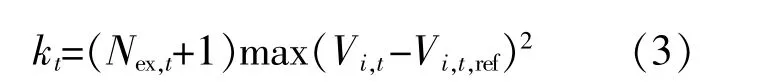
式中：Nex，t为第t时刻的电压越限节点个数。

在一年四季的不同负荷率情况下，配电网各节点电压会有较大的区别。为更全面分析得出储能较优安装位置，不同运行方式对节点电压灵敏度的影响也须加以考虑，提出计及不同运行方式的影响权重kop。

式中：dop为第op种运行方式持续天数在1 a中所占比例；Vop，i，t为第op种运行方式下的节点电压。定义节点i的电压综合灵敏度指标Li：

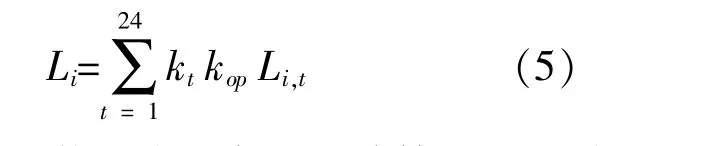
设定储能待安装节点比例n，计算配电网除平衡节点外的节点电压综合灵敏度指标，并由大到小排序。取前n个节点作为储能待安装节点集，据此筛选出一部分储能接入后改善电压质量效果更好的节点，提高储能优化布局的效率。

2 分布式储能规划模型及其帕累托求解

2.1 目标函数

为体现DES接入对提高配电网经济性和改善配电网电压质量的有效性，本文所构建的模型采用配电网电压波动以及配电网综合成本作为双目标优化函数。

（1）配电网综合成本

考虑配电网日均总成本fC最小作为优化目标，主要包括网损成本Closs、购电成本Cgrid和运行周期内的储能投资与运行维护成本Cess：

式中：Ploss，t为配电网在t时刻的有功损耗；closs为单位电量有功损耗费用，元/（kW·h）；Δt为时间间隔，本文取Δt为1 h；N为电网负荷节点集，是E的子集；Pgrid，t为t时刻上级电网注入总有功功率；PLi，t，PDGi，t分别为负荷和光伏注入的有功功率；PES1i，t，PES2i，t分别为储能充、放电功率，充电时为负，放电时为正；SPV为光伏安装节点集；SES为储能安装节点集。

购电成本：

式中：cgrid，t为t时刻的单位电量购电费用。

储能成本：考虑运行寿命损耗后的储能等值日均投资和运行维护成本。

式中：γess，i为第i个储能现值转年值系数；yess，i为第i个储能实际运行寿命；r为贴现率；Ness为储能安装个数；cep，cee分别为储能单位功率投资成本和单位功率的运行维护成本；ErES，t为第i个储能的额定容量；PES，i，t为第i个储能t时刻的充放电功率。

（2）配电网电压波动

选取配电网电压波动总和fV最小作为DES优化配置的目标函数。

式中：ΔVd为在24 h内电网节点集合中全部节点的电压波动总和；E为电网节点集合，节点i为电网节点集合内任一电网节点；Vi，t为节点i第t时刻的节点电压；Vi，t，ref为节点i的基准电压。

2.2 约束条件

为维持配电网稳定运行，所构建的储能优化规划模型须满足以下约束。

①节点电压约束

式中：Vi，min，Vi，max分别为节点i电压幅值的下限和上限。

上述约束可表示为

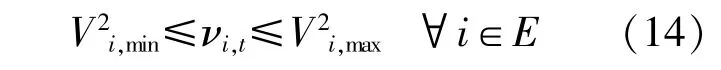
式中：νi，t为在t时段中节点i的电压幅值的平方。

②线路电流约束

式中：对于任意（i，j）∈E，节点i和节点j间线路lij的阻抗为zij=rij+jxij，有yij=1/zij=gij+jbij；Iij为由节点i流向节点j的线路电流幅值；lij，t为线路电流幅值的平方；Vi，t为在t时段中节点i的电压幅值；QLi，t，QDGi，t分别为节点i的负荷和光伏注入的无功功率；Qgrid，t为t时刻上级电网注入的总无功功率；Sij，t=Pij，t+jQij，t为在t时段中线路始端节点的复功率，且由节点i流向节点j；SG，i为储能安装位置的0-1变量，当SG，i取1时，表示储能待安装节点i处须安装储能，当SG，i取0时，表示储能待安装节点i处不须安装储能。

④分布式光伏接入配电网的有功无功运行约束

式中：Pi，tDG，pre为节点i的光伏有功功率预测值；SDG为光伏视在功率的上限；Qi，tDG为节点i光伏注入的无功功率。

⑤上级电网注入配电网的总有功功率限制约束

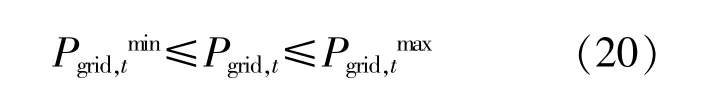
式中：Pgrid，tmin，Pgrid，tmax分别为上级电网注入的总有功功率的下限和上限。

⑥储能充放电功率限制约束

式中：PESi，max为储能设备i的充放电功率的上限；SG，i为储能安装位置的0-1变量，当SG，i取1时，表示在待安装节点i处安装储能，反之，不安装储能。

⑦储能充放电状态约束

储能设备在正常运行时，在任意时段t内只能处于充电或放电状态，即：

式中：SSG为储能待安装节点集合；Nmax为储能计划最大安装个数。

⑩24 h充放电平衡约束

正常运行时，在24 h周期内储能能量达到平衡，即：

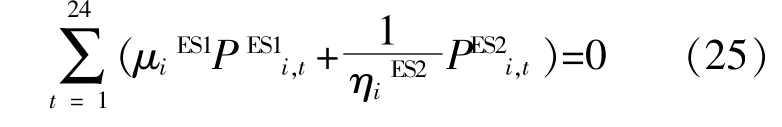
2.3 基于ε-约束法的双目标帕累托求解

一般情况下，多目标优化问题不存在唯一全局最优解，通常可以求得多个不互相支配的帕累托最优解，形成最优解集。当决策变量中含有整数变量时，运用ε-约束法求解多目标问题具有优势[17]。将一个目标选为基本目标，其他目标转化为不等式约束加以考虑，数学模型为

式中：fi（x）（i=1，…，k）为多目标问题的第i个目标，fm（x）选为基本目标；A（x）≤0为原模型中不等式约束；B（x）=0为原模型中等式约束；εi作为目标函数fi（x）的上限，对应问题的可行域随其取值不同发生变化，通过εi不同取值进行相应优化求解，可求得一系列帕累托最优解。

εi的取值范围一般根据偿付表来计算。使用ε-约束法求解所构建的双目标优化模型时，设fc为基本目标，fν转化为不等式约束，须获得fν对应的ε范围取值。其中，将fc作为单目标进行优化求解，得出的fνmax取为上限，将fν作为单目标进行优化求解，得出的fνmin取为下限，用M-1个中间等距网格点，将目标函数fν求解范围划分为M个相等间隔，每一个εi可表示为

求解出帕累托最优解集后，采用考虑主观权值修正的熵权双基点法，从解集中选取折中最优解构建评价模型，进行基于熵权法的综合评价[18]。求出考虑帕累托最优解差异程度影响的客观权值，再考虑调度人员的主观意愿，对该权值进行适当修正。采用的方法在计算相对贴近度时，综合考虑了目标函数熵权与主观权重，在计及了调度决策的主观意愿的同时，又能从客观上体现两个目标函数的重要程度。据此，将求解出的相对贴近度数值最大的帕累托最优解，选为折中最优解。

3 分布式储能优化的误差场景模拟法

光照强度和温度等天气因素会引起分布式光伏出力发生随机波动，可能导致光伏出力实际值与预测值的偏差较大，影响配电网的安全稳定运行。求解储能规划方案时，若不计及光伏出力的不确定性，会限制所得优化方案的适用性。为此，通过误差场景模拟法转化光伏出力偏离预测值的不确定波动[19]。构建包含误差场景约束和场景转移约束的模型如下：

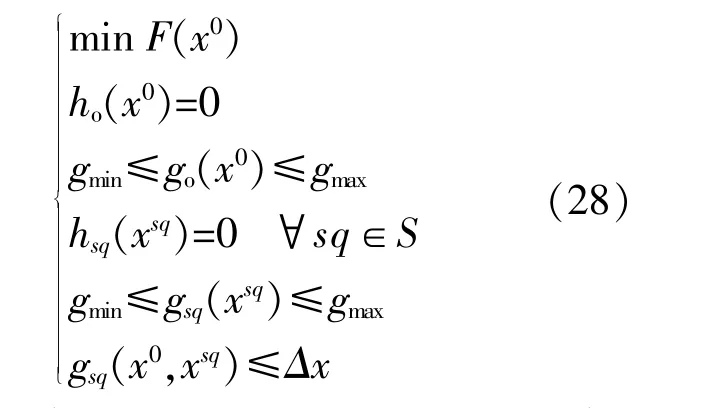
式中：x0为预测场景下的变量；F（x0）为预测场景下的目标函数；S为由不同误差场景sq构成的集合；xsq为误差场景sq下的变量；ho（x0），go（x0）分别为预测场景下等式和不等式约束；hsq（xsq），gsq（xsq）分别为误差场景sq下的等式和不等式约束。

在上述模型中，误差场景模拟法通过考虑储能的充放电功率、上级电网注入功率等其他决策变量的快速调整，以平衡光伏出力的随机波动，将不确定性问题转化为多个场景下的确定性问题。据此，规避光伏出力随机性对储能优化规划方案的影响，显著提高了方案适用性。在误差场景中，决策变量的调整须加以约束。

①充放电功率转移约束

式中：PES1i，t，sq，PES2i，t，sq为误差场景sq下储能充电功率和储能放电功率；ΔPES1i，t，ΔPES2i，t为在t时段内可调整的最大储能充、放电功率；Pgrid，t，sq为在误差场景sq下上级电网注入的总有功功率；ΔPgrid，t为在t时段内可调整的最大上级电网注入有功功率。

所建立的优化规划模型为混合整数非线性模型，模型中决策变量包含表示储能待安装节点是否安装储能的离散变量，可利用GAMS软件中的优化求解器DICOPT求解。

4 算例分析

基于修改的IEEE33节点系统的数据建立仿真算例[13]。在节点18和节点24接入分布式光伏，视在功率上限为0.8 MVA，节点最大有功负荷为0.42 MW，基准功率为1 MVA，基准电压为12.66 kV。日负荷功率及光伏出力预测曲线参考文献[14]。购电电价采用分时电价制，采用标幺值计算[13]。假设每个时段内光伏出力服从期望值为预测值的正态分布，在计及光伏出力不确定性时，考虑光伏出力随机波动的均方差δ为预测值的5%，10%，15%，20%，25%，30%的不同情况下，分别采用蒙特卡洛模拟抽样生成10个误差场景，利用误差场景模拟法进行优化求解。此外，储能充放电功率转移约束可调节量设置为储能充、放电功率上限的20%，上级电网购电功率转移约束可调节量设置为上级电网注入有功功率上限的10%。

设定储能计划最大安装数为3个，储能充放电效率为90%，储能额定容量为1 MW·h。单位网损费用closs取为0.8元/（kW·h）。储能的单位容量投资成本、单位功率运行维护成本及相关参数参见文献[20]。设定储能待安装节点比例为20%，节点电压综合灵敏度指标计算结果如图1所示。排序得到本文中储能安装节点集为{16，17，18，30，31，32，33}。

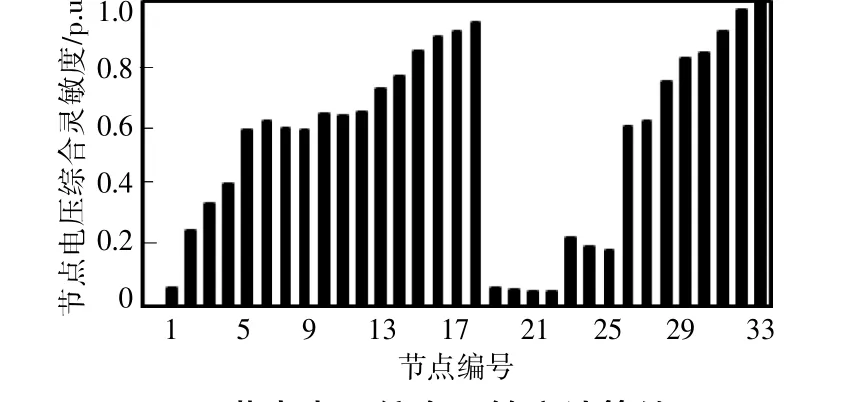
图1 节点电压综合灵敏度计算结果Fig.1 Calculation results of node voltage comprehensive sensitivity

4.1 分布式储能单目标优化配置求解

当δ设为10%的情况下，以配电网总成本为单目标优化和以配电网电压波动总和为单目标优化的最优储能充放电功率曲线如图2所示。

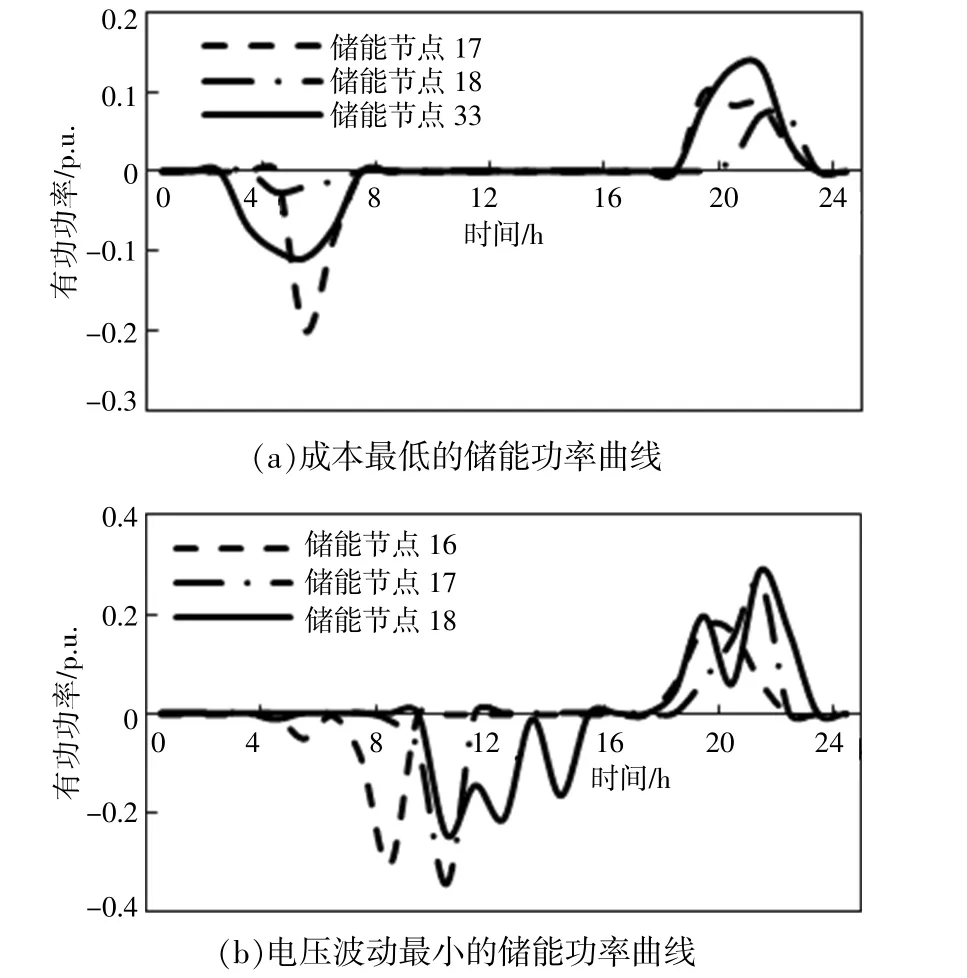
图2 储能功率曲线Fig.2 Power curve of DES

由图2可见，通过储能负荷时空转移的手段平抑配电网负载的峰谷差，有利于降低配电网总成本和减少电压波动。考虑配电网总成本最小时，计及分时电价的影响，储能在负荷谷时充电，在负荷峰时放电，起到降低配电网成本的作用。考虑配电网电压波动最小时，储能在负荷谷时与光伏出力较大时刻充电，有利于提高光伏消纳率，改善配电网电压质量，减少各个时刻的电压波动。

不同误差场景下，上级电网注入功率的对比如图3所示。图3中的实线为以成本最优为目标所得最优方案的注入功率曲线，虚线为10个误差场景下注入功率的曲线。从图3可见，上级电网注入功率在光伏波动的各误差场景下变化不大。本文构建模型中，注入功率的场景转移约束较严格，所求得的DES规划运行方案，能够促进在光伏出力随机波动的情况下配电网对光伏的消纳，降低了光伏出力不确定性对上级电网调度策略带来的影响，更好地为电网调度者提供决策参考。

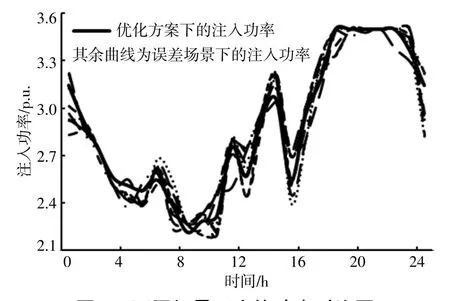
图3 不同场景下交换功率对比图Fig.3 Comparison of switching power in different scenarios

不同光伏随机波动场景下最优化配电网总成本的对比如表1所示。由表1可知，随着光伏出力不确定性的增加，购电成本和储能成本有增加的趋势，从而导致配电网运行成本有所增加。另外，对比有无储能接入的结果可知，储能的配置能够有效节省运行成本，且随着光伏波动的增加而增多。可见，DES的配置能够平抑光伏出力的随机波动，有效提高配电网的经济性。

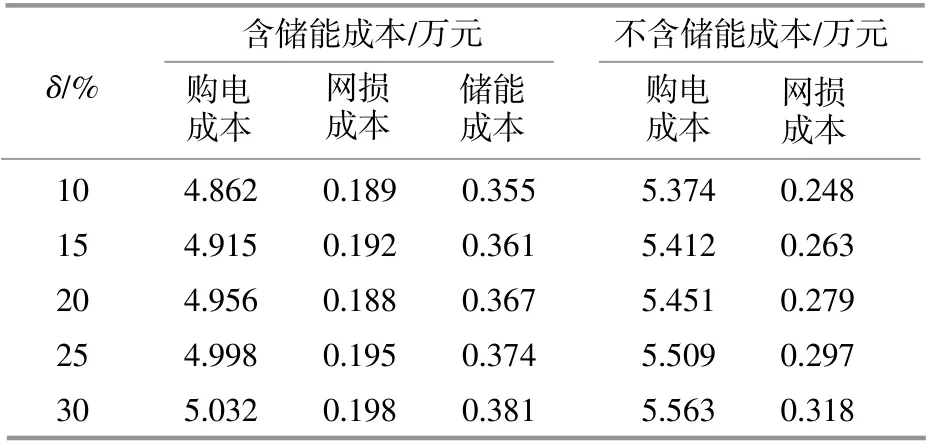
表1 不同光伏波动下总成本对比Table 1 Comparison under different %

4.2 分布式储能双目标优化配置求解

在δ为10%的情况下，利用基于ε-约束法进行双目标帕累托求解，计及主观权值修正的熵权双基点法，得出21个解组成的最优解集（图4）。从图4可见，曲线右端的帕累托最优解点集较左端的点集稀疏，说明在曲线右端增加配电网总成本对于降低电压波动的效果比较明显；在曲线左端，增加电压波动对降低配电网总成本没有显著效果。通过计算可得配电网总成本和电压波动的目标函数熵权分别为αc=0.332，αv=0.668。考虑到所求最优方案对于调度决策的适用性，计算每个帕累托最优解的相对贴近度时，须同时考虑目标函数的熵权αi与主观权重系数λi。当考虑配电网总成本目标函数的主观权重系数λc取为0，0.25，0.5，0.75，1.0时（电压波动总和目标函数的主观权重系数λv对应取为1-λc），对应的帕累托最优解已在图4标出，对应的规划结果如表2所示。

图4 帕累托最优解集Fig.4 Pareto optimal sets

表2 优化规划结果Table 2 Optimal planning results

考虑λc取为0或1时，此时为单目标优化问题；考虑λc取为0.5时，此时两个目标主观权重不影响最优解的选取。本文选取此解为折中最优解，对应的储能充放电功率曲线如图5所示。

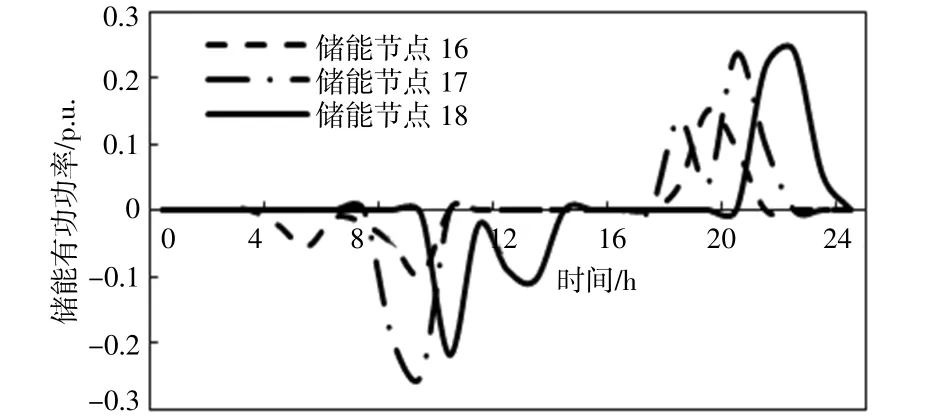
图5 折中最优解对应的储能功率曲线Fig.5 DES＇s power curve of compromised optimal solution

不计储能等值日均成本，系统每日运行成本节省0.571万元，4～5 a即可收回储能投资总成本，所求得的折中最优解对应的两个目标函数值都是相对较优的。在实际运行中，可以根据实际需求选取主观权重系数，据此求得适用于实际需求的对应帕累托最优解。

4.3 节点综合灵敏度分析方法的选址高效性

在δ设为10%的情况下，为验证所提DES优化规划模型的适用性与基于节点电压综合灵敏度方法的储能选址方案有效性，选取3个场景（1-未安装储能；2-搜索所有节点进行储能的选址配置；3-基于节点电压综合灵敏度分析进行储能选址优化）进行比较，选取折中最优解作为优化结果。

不同场景的优化结果对比如表3所示。

表3 不同场景下的优化结果Table 3 Optimal results under different scenarios

从表3可见，储能配置有利于改善电压质量、节省运行费用。场景2未进行储能预选址，计算变量维度较大，模型优化难度高，所得结果为局部最优解。基于节点综合灵敏度分析进行储能选址，降低了优化变量维度和求解计算量，节省了大量计算时间，提高了储能选址优化问题的寻优效率，同时得到更优的方案。

4.4 储能配置方案的适用性

在进行储能优化布局时，考虑了不同运行方式的影响。为了验证所得储能配置方案适用性，本文选取以下3个场景（4-选用基准日负荷预测曲线；5-为基准日负荷的1.1倍，模拟夏天配电网运行场景；6-为基准日负荷的0.9倍，模拟冬天配电网运行场景）进行比较。对于不同的场景，根据储能优化配置方案，固定储能安装位置，进一步优化储能运行策略，均选取各场景下折中最优解。

不同场景的优化结果对比如表4所示。

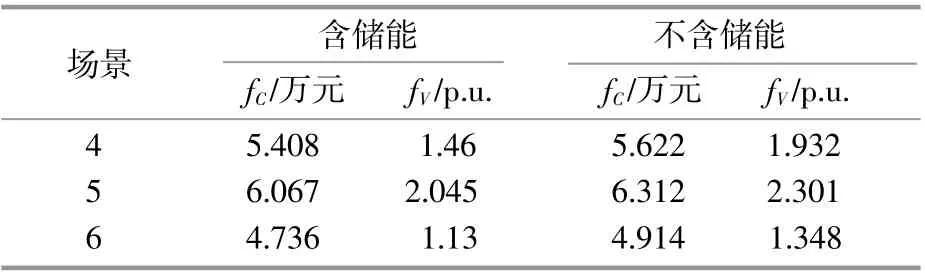
表4 不同场景下的优化结果Table 4 Optimal results under different scenarios

表4显示，本文储能配置方案能满足不同负荷场景下配电网的稳定运行要求，对不同负荷场景下配电网运行经济性和电能质量均有改善。对比显示出本文所提储能优化规划方案的适用性。

5 结论

为规避光伏出力波动对DES规划方案的影响，本文提出了一种考虑光伏随机波动的配电网DES双目标优化规划方法。算例仿真结果表明：①本文所提出的DES优化配置方法不仅能够降低配电网运行成本，减少配电网各个时刻的电压波动，还有利于平抑光伏出力的不确定波动；②所求得的DES规划方案适用于光伏出力随机波动的场景，能够降低光伏出力不确定性对电网调度策略带来的影响，方案适用性较强；③所提出的优化规划方法能够结合调度实际需求，选取适用的帕累托最优解，更好地为配电网规划与运行人员提供决策参考；④所采用的节点电压综合灵敏度分析方法，能够显著提高储能规划问题的选址寻优效率，具有不同运行场景下的适用性。