基于Markov链光伏储能模型的传输功率可用性评估

刘 飞，李雪男，张祥成，许德操，彭 飞，孙 昕

（1.国网青海省电力公司经济技术研究院，青海 西宁 810000；2.清华四川能源互联网研究院，四川 成都610000；3.国网青海省电力公司，青海 西宁 810000）

0 引言

由于昼夜交替和天气变化，光伏发电（Photovoltaic，PV）具有很大的不确定性。储能装置[1]，[2]对于平抑电网负荷波动、保证电网运行稳定性具有重要意义[3]。光伏发电和储能系统的组合将光伏系统从基于纯电力的瞬时发电系统转换为基于能源的可调度发电能源系统。为了实现一定的输出功率目标，必须量化储能装置中的充放电循环。

国内外学者已对光伏发电厂储能问题进行了大量研究。文献[4]～[6]使用多年的太阳辐射数据的月平均日值和负载确定电池的尺寸，即用月平均日值表示的容量补偿电网无法满足负荷需求的时间。该方法虽然简单，但天气条件或负载需求的巨大变化可能导致储能电池尺寸过大或系统成本增加。文献[7]～[10]利用历史数据和实验数据，将日照和负荷需求设为随机变量进行建模，估算出负载运行时间内未满足负载需求的时间，并基于电力系统的最小成本计算出电池和光伏组件的最佳尺寸，但并不能给出光伏发电满足负载需求的概率。

为解决光伏发电系统中的供电不平衡问题，本文基于Markov链储能模型[11]对光伏储能系统充电和放电循环进行建模，测量光伏储能系统为电网负载供电的概率，进而评估使光伏发电达到所需可用性水平的最佳储能规模。建立的模型不仅能实现更有效的储能规模和整体电网资产规划，还可以防止过度循环导致的电池寿命缩短以及电池成本升高。

1 Markov链储能模型的建立

设S为所有PV源的集合，若Xi为第i个PV源提供的功率，则PV源提供的总功率Xr可以表示为

光伏储能系统可用性A可定义为光伏发电厂能够向负载提供足够的电能并为储能装置充电的概率，即：

式中：P为条件概率：L为光伏系统提供的负荷功率。

由于发电可用性应大于所需负载可用性，当光伏组件用作唯一的发电源时，如果没有储能，就无法满足可用性需求。

通常会基于PV日照数据对存储容量进行计算。文献[12]中使用Markov链模型将可用性和存储容量联系起来，模型如图1（a）所示。仅考虑相邻状态之间的单位时间内能量转换，每个整数代表一种荷电状态（State of Charge，SOC），状态1表示完全放电状态，状态N表示完全充电状态。仅考虑相邻状态之间的转换意味着L假定为常数，随机变量Xr取值只要两个，但这不符合实际。因此，本文对该模型进行了拓展，允许（Xr-L）在一个有限集合中取值。

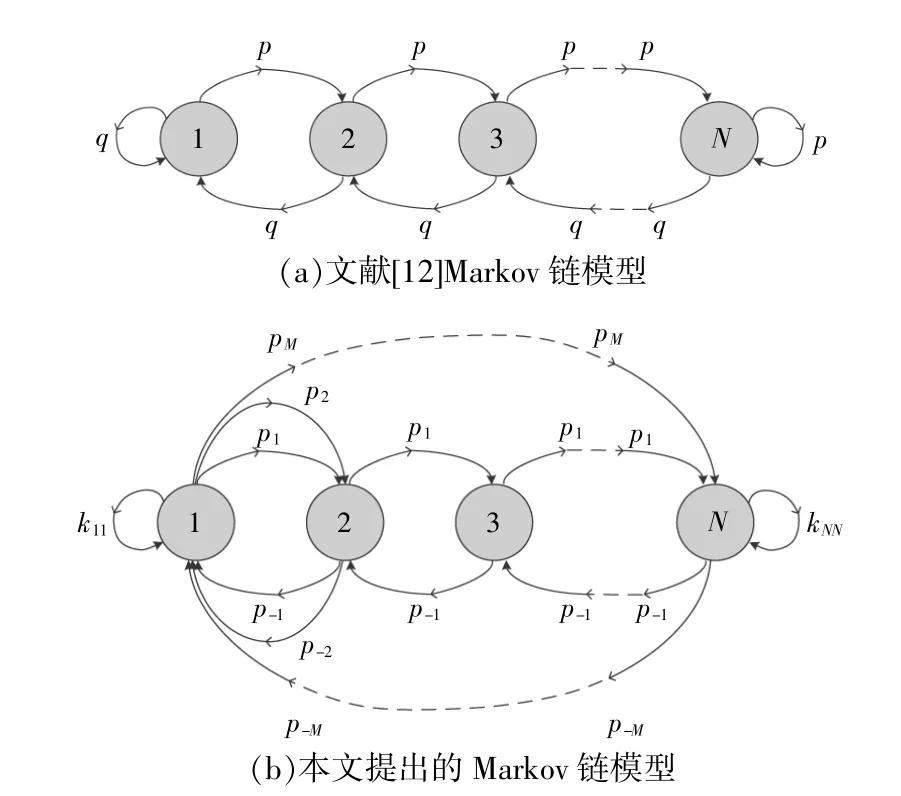
图1 基于Markov链的电池状态转换Fig.1 Markov-chain-based battery state transition

本文提出的Markov链模型如图1（b）所示。该模型考虑了多种可能的状态变化，更符合电池的充放电特性。特别地，对电池状态转换进行了建模，在每个时间步中，每个状态中有M个转换。图中：k11和kNN分别为在下一时间步保持状态1和状态N的概率；pi为状态之间的转移概率，其中i为观测状态。例如：p1是向相邻状态的过渡，每单位时间内存储到蓄电池的功率为Δ；而p-1是向相邻状态的过渡，每单位时间内从蓄电池中获取的功率为Δ。此外，（Xr-L）的状态扩展为

假设充电和放电过程是线性的，那么存储容量C可以表示为

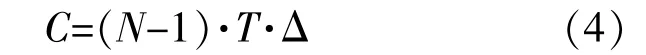
式中：T为能量交换的时间，因为假设状态1表示电池中没有存储能量时的状态，并且需要M=N-1达到状态N（电池在其最大SOC下的状态），在连续过渡到相邻状态中，单位时间内有ΔE的能量转移，即每个过渡涉及的功率等于Δ。

为了更详细地分析图1（b）中所示的Markov链，假设D为在时间T内传输到电池单位时间内的预期能量，则有：

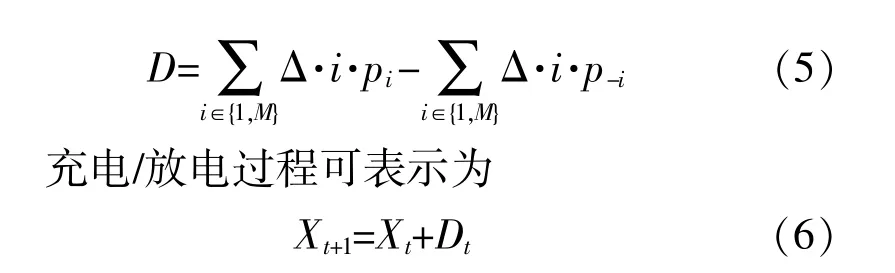
式中：Xt为t时的能级；Xt+1为1 s后的能级；Dt为1 s内向蓄电池存储或获取的能量，即Dt=DT，T=1 s。

由图1（b）中的Markov模型所产生的电池充放电过程的转移概率矩阵为

式（7）的矩阵大小为N×N，其中，N为电池充电/放电过程被量化的状态总数，pi由光伏发电和负荷分布直方图获得。式（8）～（11）使用Markov链特性进行评估，表示任意行总和等于1。此外，在稳态下极限概率可表示为[13]

其中π符合稳态分布。极限概率表示每个状态结束时的预期概率。极限概率已知后，可求取失负荷概率（Loss of Load Probability，LOLP）。LOLP是指电池处于SOC时在Markov链中过渡到完全放电状态无法满足i个单位功率Δ的概率。用πE表示光伏储能系统不能满足负载的概率，则特定储能容量的LOLP可确定为

举例说明如何使用式（13）确定LOLP。假设状态5的转移概率如式（14）所示，可以联立式（7）～（11）来确定一步转移概率矩阵，结果如式（15）所示。

将式（14）中的参数分别带入式（12）中，可得极限概率结果，如式（16）所示，进而可得πE结果，如式（17）所示。

2 Markov链储能模型的实现

能量存储容量和可用性之间关系的完整计算过程流程图如图2所示。首先使用蒙特卡洛方法，根据太阳光入射功率和负荷分布的概率密度函数，生成日间光伏功率和负荷的随机值；然后生成光伏组件产生的功率与负荷消耗的功率之间的差值直方图。直方图显示了一定能量值转移发生的频率。利用直方图，以转移概率为输入，求出一步转移概率矩阵，并计算极限概率；最后，对不同尺寸的储能装置的可用性和储能容量进行评估，建立这两个指标之间的关系。

图2 可用性计算过程流程图Fig.2 Block diagram of an availability calculation process

2.1 随机值生成

①PV输出功率随机值生成

光伏发电数据从某一光伏发电厂获得，时间为1-7月，每天7：00-19：00，间隔5 min。如图3所示，光伏入射功率的最大值约为1 kW/m2。为了得到光伏入射功率的概率密度函数，生成了频率分布直方图，如图4所示。由图4可见，直方图满足式（18）的指数分布。

图3 1-7月每天7：00-19：00的光伏发电功率Fig.3 Incident PV power collected from 7：00-19：00 for 1-7 months

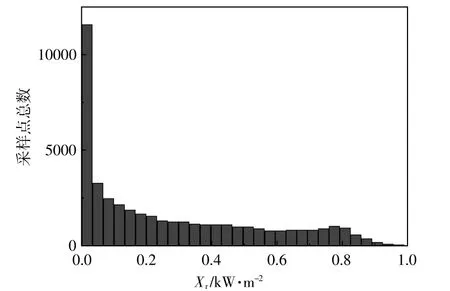
图4 图3 中光伏入射功率直方图Fig.4 Histogram of incident PV power from Fig.3

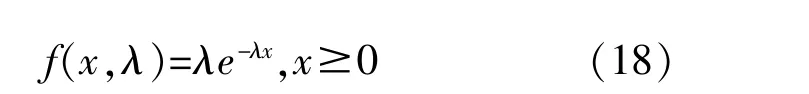
使用Matlab对图4进行拟合，可得到率参数λ=0.003 8。使用蒙特卡洛方法，根据式（18）中的概率密度函数生成随机值。在蒙特卡洛方法中，假设在10 a内每5 min测量一次光伏入射功率，则会生成100多万个随机点，这些随机点的直方图如图5所示。可见，图5和图4中的直方图形状近似。用生成的光伏入射功率随机值以及光伏组件的市场规范可以估算光伏发电厂的输出功率。例如，某个250 W光伏板的效率为15.3%，面积为1.51 m2[14]。假设光伏发电厂中有该型号的光伏板10 000块，则总容量为2.5 MW，面积为15.1 km2。通过计算，该光伏发电厂在7：00-19：00将产生608.22 kW（标准偏差为618.35 kW）的平均功率。

图5 λ=0.003 8时的光伏入射功率随机值直方图Fig.5 Histogram of the generated random values of incident PV power（λ=0.003 8）

②负载随机值生成

为了确定单位时间内的总能量传输，本文采用负荷曲线与光伏发电曲线相结合进行计算。负荷数据集是从文献[15]中获得的，为期1 a。负荷曲线如图6所示。可见，每户1 d的平均用电量为17.62 kW·h。

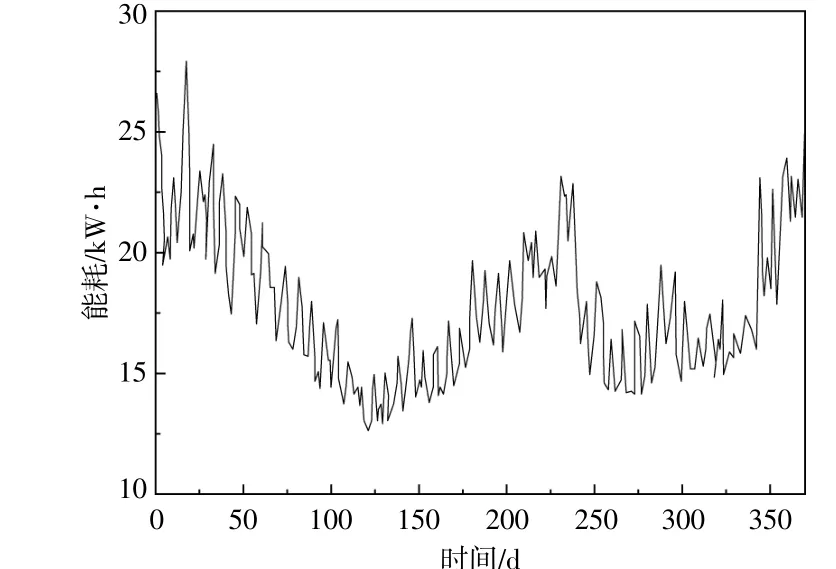
图6 1 a内每户的平均电能使用量Fig.6 The average energy usage per household for 1 year

图7和图8分别显示了每户白天（7：00-19：00）和夜间（19：00-7：00）的负荷功率直方图。可以看出，白天的负荷功率总体大于夜间。而且图7和图8符合式（19）中所示的瑞利分布，用Matlab可得标准差σ白天=0.577 2，σ夜间=0.501 3。

图7 白天负荷直方图Fig.7 Histogram of the incident load during daytime

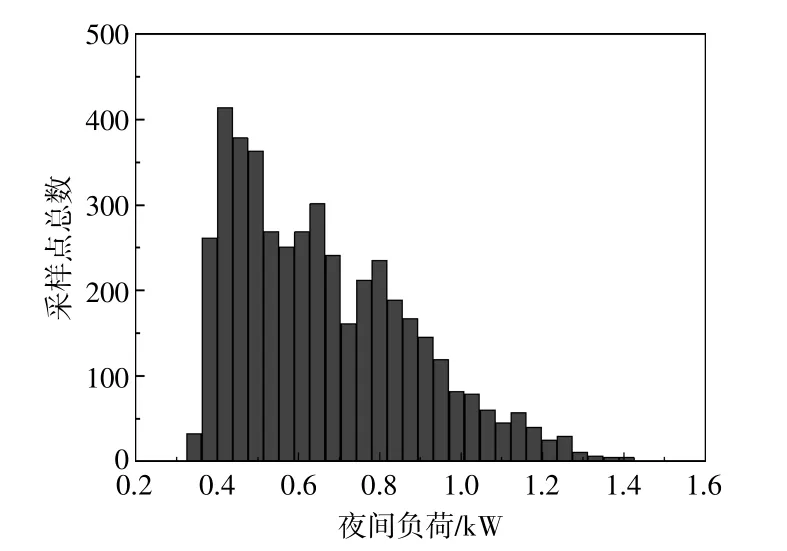
图8 夜间负荷直方图Fig.8 Histogram of the incident load during nighttime

根据上述瑞利分布，生成了100多万个随机负载值，与光伏入射功率随机值的数量相同。图9和图10分别显示了每户生成的白天和夜间的负载随机值直方图。

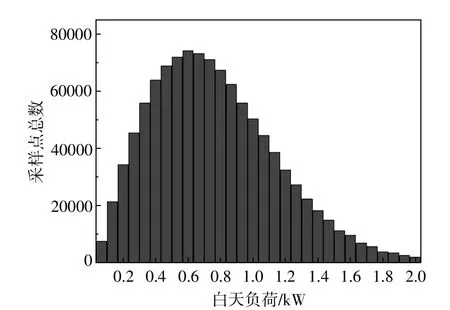
图9 σ白天=0.577 2，白天负载随机值直方图Fig.9 Histogram of the generated random values（σdaytime=0.577 2）of incident load during daytime

图10 σ夜间=0.501 3，夜间负载随机值直方图Fig.10 Histogram of the generated random values（σnighttime=0.501 3）of incident load during nighttime

2.2 传输功率计算

假设有300户家庭作为负载，白天平均功耗为238.37 kW（标准差为56.16 kW），夜间平均功耗为202.14 kW（标准差为66.18 kW），连接到容量为2.5 MW的光伏发电厂，可以通过随机生成的光伏入射功率（PPV）减去随机生成的负载值（P负荷）得到功率传输（P传输）。

为了得到用户一整天的充放电过程，将图9和图10中的负载值相加，负荷数据结果如图11和式（20）所示。

图11 用户一整天的负荷随机值直方图Fig.11 Daily load random value histogram of each household

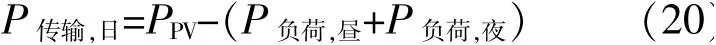
显然，将两个独立的负荷数据集结合起来会产生更大的负荷值，这在现实中是不可能观察到的，但可以解释为光伏发电厂不仅在白天满足负荷需求，而且还提前储能以备夜间使用。假设PV和负载的100多万个数据值足以模拟该充放电过程，则蒙特卡洛模拟能够使用式（20）进行功率传输分布估计。图12为用于功率传输生成的随机值直方图。由图可见，为储能系统充电的最大功率约为2 300 kW，电池放电的最大预期功率约为1 000 kW。

图12 2.5 MW光伏发电厂和300户家庭负荷之间产生的功率传输随机值直方图Fig.12 Histogram of the generated random values of power transfer between the 2.5 MW PV power plant and 300 housing load

一方面，光伏储能系统可自动或作为电网集成系统的一部分与多个电源一起向负荷供电。在自主操作的情况下，所提出的模型可以直接应用；另一方面，当光伏储能系统接入电网时，电池完全充电时，会向电网提供额外的电能；当光伏储能系统没有足够的电能满足需求时，电网会为负载供电。因此，当光伏系统并网后，P＇传输=（PPV-P负荷）+P电网。

2.3 转移概率

可用图12计算式（7）的转移概率pi，因为pi可以通过功率传输值的点总数除以样本点总数来确定。假设不考虑任何传输损耗，且式（4）中的Δ和N分别为20 kW和151，可得式（7）中的一步转移概率矩阵为

2.4 极限概率

得到一步转移概率矩阵后，通过式（12）得到极限概率为

极限概率显示了任意时间点Markov链模型中处于每个能级的状态的概率。在式（22）中，π151为0.305，表示处于储能系统满能级状态的概率为0.3 05。

2.5 可用性与储能容量的关系

式（13）使用极限概率和一步转移概率矩阵来求πE。由于πE表示光伏储能系统不能满足负载的概率，因此可用性可通过下式进行计算：

由于极限概率将随着储能容量的变化而变化，而πE计算与极限概率有关，因此，可以认为储能容量变化会导致πE变化。当πE与储能容量的关系已知时，由式（4）可知，通过改变状态数N来改变储能系统容量，可以找到光伏系统可用性与储能容量之间的关系。假定式（4）中的Δ，N和T分别为20 kW，151和1 h时，储能容量为3 MW·h。则由式（21）和式（13）可得式（23）中的可用性为0.995 1。

此外，通过大量不同容量值的计算机模拟，也可以确定可用性和储能容量之间的关系，如图13所示。例如，当容量为2.5 MW的光伏发电厂为300户家庭供电并希望保持0.999 9的可用性时，使用图13中的曲线可得所需的储能容量约为6.336 MW·h（0.6 d×24 h×440 kW）。该结果不仅显示了实现特定可用性需要多少储能容量，而且还显示了不同储能容量如何影响可用性。

图13 可用性与储能容量关系曲线Fig.13 Availability versus storage capacity curve

3 储能容量降低对可用性的影响

3.1 储能容量降低

老化过程会导致电池的功率和储能容量下降，这是电池不可避免的。因此，当电池作为存储系统时，电厂的实际可用性评估需要考虑电池容量的退化。

设η为老化导致容量下降后的相对容量，则系统储能容量可表示为

由于Δ是单位时间内与存储设备交换的能量，式（24）可以看成Markov链状态之间交换的能量以相同的容量退化率减少。令Δ＇=Δ×η，则有：

导致电池老化有3个因素：温度、开路电压和放电深度。为了简化分析，只考虑由温度引起的容量退化，如图14所示。可以看出，环境温度会导致容量不同程度的下降。假设光伏发电厂的电池具有与图14中电池相同的容量退化特性，且放电深度的影响可忽略不计，则可确定可用性和温度引起的容量退化之间的关系。

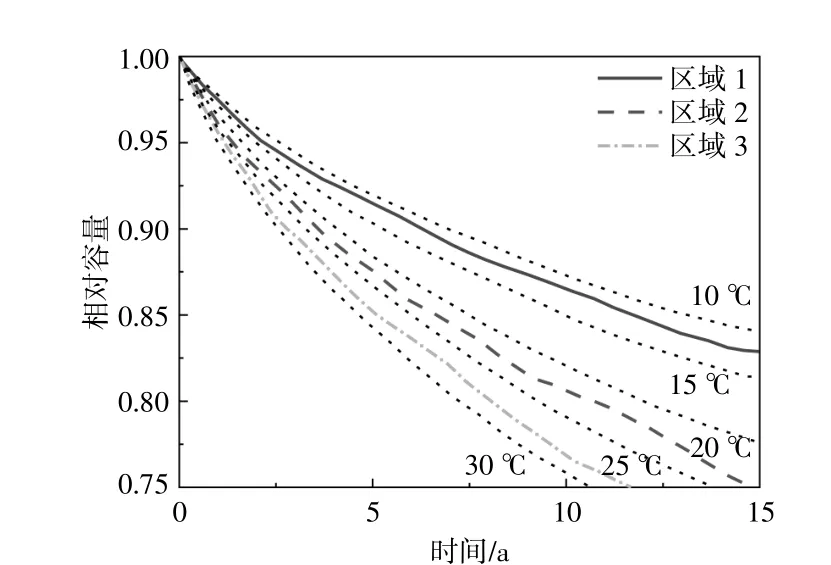
图14 环境温度对电池容量的影响Fig.14 Effect of ambient temperature on battery capacity

由图14可知，在3个不同区域工作10 a的锂离子电池产生的相对容量η分别约为0.87，0.81和0.77。当为每个位置确定Δ＇时，可以显示温度对容量退化的影响。图15显示了使用所提出的Markov链模型并将式（25）应用于计算过程的模拟结果，可见，每个位置的可用性都会随着电池容量的降低而降低。这一结果表明，当容量退化后的相对容量与温度、开路电压和放电深度等因素的关系[16]已知时，可用性降低的程度可以使用所提出的Markov链模型确定。

图15 使用所提出的Markov链模型计算温度对电池容量影响的模拟结果Fig.15 The proposed Markov chain model is used to calculate the simulation results of the effect of temperature on battery capacity

3.2 充放电效率

充电和放电效率会影响光伏组件和负载与电池之间的功率传输量，功率传输效率可表示为

式中：α和β分别为充电和放电效率。

当电池为负载和光伏组件充电时，传输量为正；当电池放电时，传输量为负。特别是，1/β表明放电功率可能大于提供给负载的功率。例如，当β=0.8时，1/β=1.25，这表明蓄电池的放电功率是提供给负载功率的1.25倍。

α和β影响充、放电量。在考虑α和β后，有：

式中：α（PPV-P负荷，昼）和（1/β）（PPV-P负荷，昼）分别为白天充放、电功率；（1/β）P负荷，夜为夜间放电功率。

图16展示了充电和放电效率如何影响功率传输，当电池效率降低到80%后，正功率传输减少，负功率传输增加。

图16 不同电池效率下随机功率传输值直方图Fig.16 Histogram of random power transmission value under different battery efficiency

功率传输值的变化导致转移概率pi的变化。因此，可以根据新的转移概率确定一步转移概率矩阵。按照第2节中的步骤，可以得到电池容量和各种效率的可用性之间的关系，如图17所示。

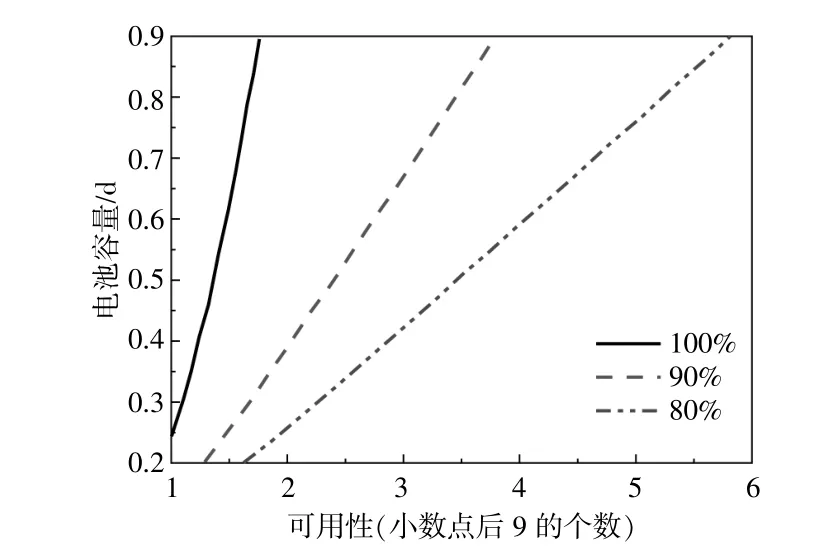
图17 不同电池效率下可用性与电池容量关系Fig.17 Relationship between availability and storage capacity under different battery efficiency

4 结论

为了量化光伏发电输出功率的可用性，本文基于光伏储能系统能量状态的Markov链，建立了光伏组件与储能系统之间的能量传递过程模型。该模型考虑了白天和夜间负荷的随机性和白天光伏发电的随机性，以及夜间光伏系统的确定性零输出，然后用实际太阳光照和负荷数据对该模型进行了验证。结果表明，所提出的Markov链模型可以使光伏发电变得更具有可调度性以及最佳的储能规模，避免容量过大导致的系统成本增加或容量过小导致的可用性不足。提出的模型可以更好地帮助理解光伏储能系统中的储能充放电效率的发生，以及如何影响光伏发电厂的供电可用性。此外，介绍了不同工作温度引起的电池容量下降对传输功率可用性的影响，导致容量退化的储能老化过程可以应用于该模型，并通过数值计算得到了容量退化与可用性之间的关系。