分布式光储直流微电网滑模自抗扰鲁棒运行控制
2022-11-23戴腾飞茅靖峰吴爱华丁寅佳
戴腾飞,茅靖峰,吴爱华,丁寅佳
(南通大学 电气工程学院,江苏 南通 226019)
0 引言
光储直流微电网可以高效吸纳光伏能源、满足用户直流需求[1]~[3]。在光储直流微电网中,光伏阵列(PV)与电池储能系统(BESS)通过电力电子变换器接入直流母线。PV系统常设置为主功率供给电源,BESS作为辅助电源,以维持直流微电网内功率平衡、抑制直流母线电压的波动。
虽然直流微电网控制目标仅是保持有功功率平衡,维持直流母线电压的稳定,但电力电子系统的高度非线性、PV系统的复杂间歇特性和随机变化的负荷需求,使得高鲁棒性母线电压控制策略成为光储直流微电网应用中的重要研究内容[3]~[6]。文献[7]给出了一种光伏发电和BESS系统直流微电网结构,设计了最优功率流的能量管理策略以维持母线电压、满足负荷供电需求。文献[8]提出了含光伏发电、柴油发电机和BESS的孤立型直流微电网结构,并通过对三者的能量管理,达到保持母线电压稳定的目的。文献[7],[8]从各发电电源的稳态方程出发,利用平均能量模型计算管理各电源输出,实现网内功率平衡和电压稳定。该类方法对于复杂的光强照度和环境变化缺乏鲁棒适应性,不利于满足动态负载的供电需求。文献[9]提出了采用增益调度法和集中模糊逻辑控制法,进行直流母线电压控制调节的组合策略,实现了功率的动态平衡和母线电压的稳定。然而,该方法未考虑可再生能源的间歇性功率输出特性,虽然模糊控制易于实现,但在逻辑规则设计和控制精度方面存在较大改进空间。文献[10]提出了模型预测电压控制策略,利用各发电电源的线性化模型来设计电压闭环控制律。基于线性模型的预测控制器只局限于有限的运行工作区间和精确的模型参数辨识,在广域运行范围的适应性和抑制外部不确定扰动的鲁棒性方面存在不足。文献[11]提出了非线性滑模控制器(SMC)来控制BESS的充放电和直流母线电压。
本文为提升光储直流微电网母线电压的控制性能,利用自抗扰控制技术(ADRC)和SMC控制理论,构造设计光储系统滑模扩张状态观测器(SM-ESO)和滑模非线性状态误差反馈(SMNLSEF)电压闭环控制律。设计PV系统指数变步长扰动观察法MPPT控制算法,以及BESS系统稳压SM-ADRC控制算法,以实现网内光储多源功率的合理分配和母线电压的动态稳定控制。在实验验证方案中,设置了光照强度和负载功率恒定、波动等3种仿真方案,实验结果验证了所提出MPPT控制算法的有效性。基于滑模的自抗扰控制能抑制功率扰动,维持母线电压稳定,使微电网内功率平衡更具有快速性和稳定性。
1 光储直流微电网结构原理
图1为光储直流微电网总体结构。

图1 直流微电网系统典型结构Fig.1 Typical structure of DC microgrid system
图中:Ppv,Pbess,Pload,Pnet分别为光伏输出功率、BESS输出功率、直流负载吸收功率和母线总功率;vdc,Cdc分别为母线电压和母线等效电容。
光储直流微电网的总功率Pnet平衡方程为

式中,BESS输出功率在充电模式下为负,在放电模式下为正。在所有运行条件下,直流母线电压恒定是确保微电网稳定运行的首要任务。稳态恒电压条件下,母线净功率保持为零,即Pnet=0。在动态条件下,功率与电压可表示为
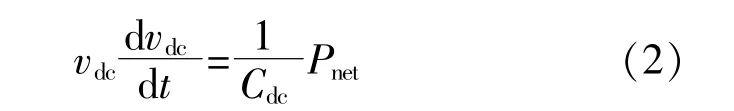
由式(2)可知,维持直流母线电压恒定是保证直流微电网内部功率平衡的关键因素。
2 光储直流微电网数学模型
2.1 光伏发电系统数学模型
PV阵列的等效电路如图2所示[12]。
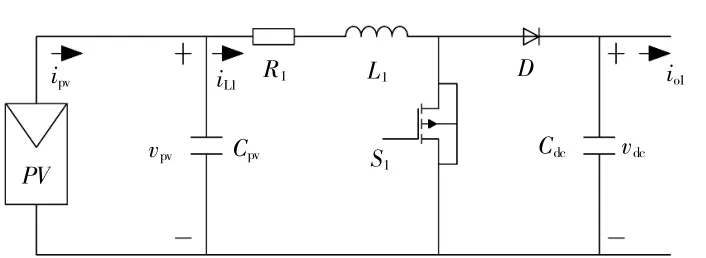
图2 光伏发电系统等效电路Fig.2 Equivalent circuit of photovoltaic power generation system
图中:vpv,Cpv,ipv分别为光伏阵列输出电压、滤波电容和输出电流;R1,D,L1,iL1分别为升压变换器电阻、二极管、电感和电感电流;io1为直流系统等效负荷电流。
光伏阵列输出通过DC-DC升压变换器接入直流母线。由于太阳能光照功率的间歇性,常采用MPPT策略控制升压变换器,使得光伏发电系统的输出呈现为恒功率源(CPS)特性。
若电力电子开关S1的占空比控制量为μ1,则图2模型为[13]

2.2 BESS系统数学模型
BESS系统等效电路如图3所示。图中:vg,Cg分别为BESS蓄电池组端口电压和滤波电容;L2,RL2,iL2分别为双向DC-DC变换器的电感、电感寄生电阻和电感电流;id为流过电力电子开关S3的电流;io2为直流系统等效负荷电流;R2为阻性负载;PCPL为恒功率负载的功率;iCPS为恒功率源的输出电流。

图3 BESS系统等效电路Fig.3 Bess system equivalent circuit
若电力电子开关S2的占空比控制量为μ2,则BESS系统数学模型为[14]

3 控制器设计
在直流微电网中,各个分布式单元参数均为时变非线性参数,并且在运行过程中环境复杂不确定,导致系统难以维持长期稳定状态,因此直流微电网的鲁棒稳定运行控制非常重要。本文对光伏发电系统采用变步长扰动观察法MPPT控制,对BESS系统采用滑模自抗扰非线性控制,以获得良好的电压鲁棒控制效果。
3.1 光伏发电系统MPPT控制器设计
光伏电池的输出特性主要指输出电流与输出电压之间的关系和输出功率与输出电压之间的关系,其变化曲线如图4所示。
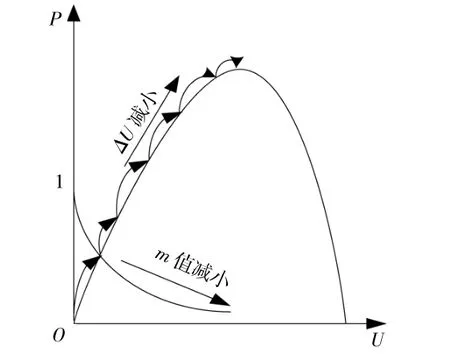
图4 MPPT步长变化示意图Fig.4 Schematic diagram of MPPT step change
本文采用基于功率变化指数变步长扰动观察法进行MPPT控制,通过调节占空比μ1实现。在传统的定步长扰动观察法中,引入电压增量ΔU的时变平滑因子m,m取值在(0,1)。m值的确定与距离最大功率点的距离有关。当距离最大功率点较远时,m取值大;反之,m取值小。这使得步长ΔU不再是一个常数值,而是随着时变因子m变化的一个函数值[17],在远离MPP时,P-U特性曲线斜率大,即ΔP增量较大,在接近MPP时斜率变小,P增量较小。依据ΔP的变化,改变m的值的大小,当ΔP较大时,步长取值大,m取值接近于1;当ΔP较小时,m取值较小。ΔP直接通过指数函数映射为m的值。m取值随着ΔP的变化而发生实时的变化,表达式为

指数变步长扰动观察法控制的具体流程如图5所示。

图5 指数变步长扰动观察法控制流程图Fig.5 Control flow chart of exponential variable step disturbance observation method
该方法首先测量当前工作点的电压电流U,I,并通过上一个工作点确定计算出ΔP,ΔU,然后由指数函数运算得到时变因子m的值,得到下一步工作点的步长。通过比较ΔP,ΔU值的正负,进而确定下一工作点的给定电压参考的扰动方向,最终获得下一工作点的电压值Uref*=Uref±mΔU。
3.2 BESS系统ADRC控制器设计
自抗扰控制(ADRC)具有不依赖于系统模型和鲁棒性强的优点。ADRC主要由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEF)组成。
由式(4)可知,直流母线电压vdc受到输出电流io2、恒功率负载、母线电容Cdc、阻性负载R2的耦合作用,要提高母线电压的稳定性,必须克服被控对象的不确定性干扰。根据式(4),直流母线电压vdc的数学模型为

式中:b为控制增益,b=iL2/Cdc;w(t)为扰动项,w(t)=(-vdc/R2-PCPL/vdc+iCPS)/Cdc。
首先,设计输入跟踪微分器,以获取控制器跟踪母线给定电压v*dc合理过渡过程,表达式为
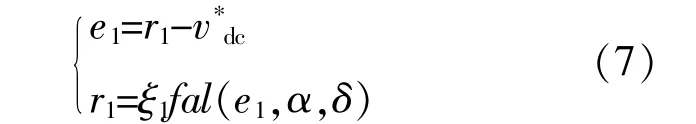
式中:e1为母线给定电压跟踪误差信号;v*dc为直流母线电压给定值;r1为v*dc跟踪信号;ξ1为跟踪速度因子;fal(e1,α,δ)为非线性幂次函数,即:

式中:α为非线性因子,0<α<1;δ为滤波因子,δ>0;sgn(x)为符号函数。
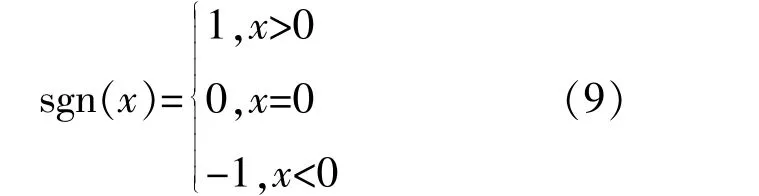
其次,设计扩张状态观测器,以估计出控制系统中不可测的综合扰动量,表达式为

式中:e2为母线电压跟踪误差信号;z1为直流母线电压的跟踪信号;变量z2为综合扰动项w(t)的观测值;β1,β2为输出误差校正增益;α2为非线性因子;δ2为ESO滤波因子。
最后,设计非线性状态误差反馈控制律,以完成闭环控制系统的综合和构造,表达式为

式中:e3为状态跟踪误差信号;λ为控制增益参数;u0为过渡过程与状态观测之间误差的非线性组合,利用它和扰动估计量的补偿来生成最终控制信号,其物理含义为最终控制量占空比μ2扰动补偿前的误差反馈控制,即初始控制信号。
3.3 BESS系统SM-ADRC控制器设计
在BESS系统ADRC控制器中,ESO和NLSEF的可调参数多且不易整定。通过将SMC和ADRC控制方法相结合,可将滑模控制方法引入到ESO和NLSEF的构造中,设计滑模扩张状态观测器(SM-ESO)和滑模非线性状态误差反馈控制律(SM-NLSEF),以改善参数整定和控制器的控制性能,减少可调参数,提高系统的响应速度和鲁棒性。
将BESS双向DC/DC变换器视作单输入单输出系统,SMC设计包括滑模切换函数s(x)和滑模控制律两部分,通过李雅普诺夫稳定性理论约束,确保被控系统在有限的时间移动到滑动模态s(x)=0。
3.3.1 滑模扩张状态观测器设计
根据ESO和SMC的设计原理,将式(10)改写为

式中:zj2为非线性函数组合;h1(e2)和h2(e2)为待设计的最优函数,即通过设计恰当的函数,以实现对BESS双向DC/DC变换器系统扰动项的进行估计。
定义误差函数为

令w*(t)=a1(t),并保证a1(t)≤θ,θ为有界常数。由于实际BESS系统中扰动值是有限的,因此,a1(t)为有界函数。
可构造ESO滑模切换函数为

式中:c1为滑模切换函数系数,c1>0。
定义

式中:ε1和q1为可调增益参数,ε1>0,q1>0。
为了保证滑模切换函数s1快速收敛,趋于稳定,根据式(13)~(15),可设计最优控制函数H(e2)的表达式为

选取李雅普诺夫函数V1=s12/2,得到SM-ESO的具体表达式为

3.2.2 滑模非线性状态误差反馈控制律设计
根据式(12),由NLSEF和SMC的设计原理,可得:

式中:g(e3)为待设计的最优函数。
构造NLSEF滑模滑模切换函数:

式中:c3滑模切换函数系数,c3>0。
为了保证滑模控制系统能够快速收敛,定义

式中:ε2,q2为可调增益参数,ε2>0,q2>0。
将式(21)求导,并由式(19),(21)得:
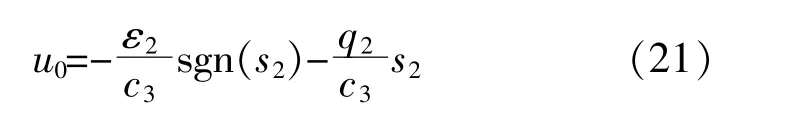
选取李雅普诺夫函数V2=s22/2,最终SMNLSEF的表达式为

得到基于SM-ADRC的光储直流微电网母线电压控制结构,如图6所示。

图6 SM-ADRC总体控制结构框图Fig.6 SM-ADRC overall control structure block diagram
4 实验验证与分析
为了验证所提出的直流微电网滑模自抗扰鲁棒运行控制方法的有效性和正确性,采用Matlab/Simulink进行仿真研究,其中系统光伏发电参数:最大功率10 kW;开路电压37.2 V;短路电流8.62 A;最大功率电压30.2 V;最大功率电流8.1 A;Cpv的标准值10μF;Lpv的标准值5 mH;Rpv的标准值0.005Ω。BESS模块参数为电池容量100 A·h;电池的开路电压300 V;Cg的标准值1μF;RL2的标准值100Ω;L2的标准值0.01 H。滑模自抗扰控制器中TD,SM-ESO和SM-NLSEF 3个组成部分功能相互独立,可采用分离性原则,分别进行参数设计。各参数优选为α1=0.8,α2=1.2,α3=1.6,δ1=δ2=δ3=0.1,ξ1=4,λ=6,β1=300,β2=30 000,b0=500,c1=100,c3=200,ε1=0.5,ε2=1.2,q1=q2=1 500。
4.1 PV系统指数变步长扰动观察法控制验证
设初始光照强度为1 000 m2/W,温度为25℃。PV系统指数变步长扰动观察法MPPT仿真波形如图7所示。

图7 恒温恒光强MPPT仿真Fig.7 MPPT simulation of constant temperature and constant light intensity
由图7可见,光伏发电最大功率点跟踪控制系统的响应速度很快,到达稳定的最大功率输出点时大约为0.01 s。系统输出功率稳定在177.77 W左右,振幅大约为0.02 W,展现了较高的稳态精度。仿真结果说明提出的MPPT控制策略不仅具有高稳态精度和高响应速度,并且不受扰动步长的选取的干扰,解决了扰动步长选取对控制系统的稳态精度和响应素的之间矛盾的影响。
假设保持环境温度25℃不变,光照强度分别为1 000,900,800 W/m2,且每阶段保持0.2 s,然后再回到1 000 W/m2,PV系统指数变步长扰动观察法MPPT仿真波形如图8所示。

图8 恒温变光强MPPT仿真Fig.8 MPPT simulation of constant temperature and variable light intensity
由图8可见,当环境温度保持25℃不变,光照强度分别在0.2,0.4和0.6 s发生改变时,所提MPPT控制策略对光伏发电最大功率点跟踪的响应速度、稳态精度和动态过渡过程均良好。
4.2 BESS系统SM-ADRC控制验证
首先假设太阳能光伏系统在标准大气条件下运行,初始光照强度为500 W/m2,温度为25℃,额定母线电压vdc=600 V。
4.2.1 光照强度和负载需求恒定
该条件下,假设太阳光照强度和负载需求恒定,且PV系统的输出功率低于负载,须太阳能光伏单元的DC-DC变换器与BESS的双向DC-DC变换器共同输出功率以满足负载需求。在仿真初始时刻,负载消耗恒定为PCPL=3 kW,根据欧姆定则,iCPL=5 A。
图9为仿真输出波形。

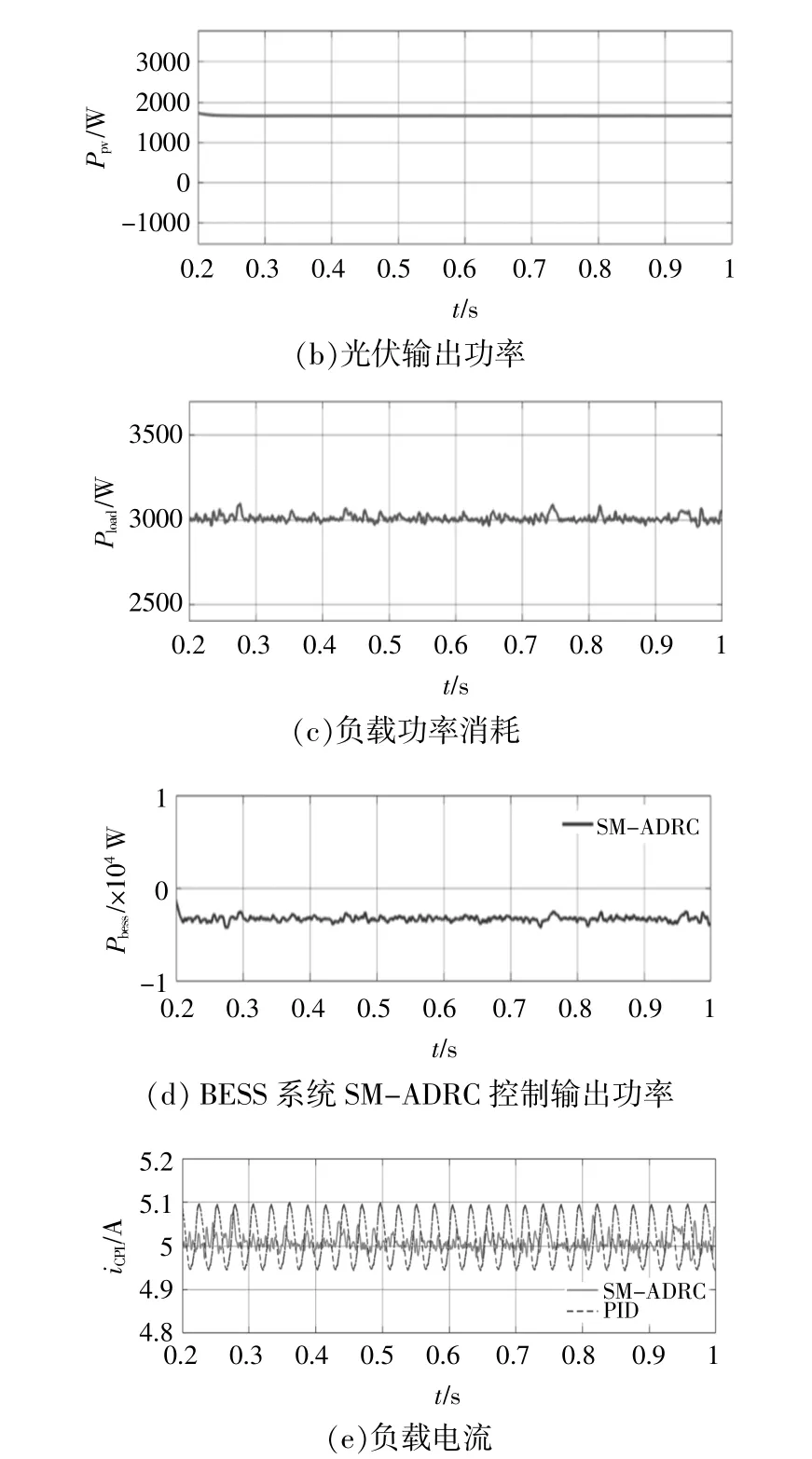
图9 方案1微电网输出特性Fig.9 Scheme 1 microgrid output characteristic
由图9可知:直流微电网母线电压基本稳定,但PID控制母线电压呈现振荡波动,最高值为611 V,最低值为592 V;SM-ADRC控制母线电压最高振荡点为605 V,最低振荡点为596 V。由此说明,SM-ADRC比PID母线电压控制更加稳定,振荡更小。PV系统在0.2 s进入稳态,MPPT控制算法计算出最大输出功率维持在1.5 kW左右,则Ppv=1.5 kW。PV系统输出功率不受直流微电网影响,仅受太阳辐射水平、温度的影响。负载功率消耗在0.2 s进入稳态,恒定为PCPL=3 kW,说明直流微电网系统总功率达到平衡,Pload=3 kW。BESS系统作为维持母线电压的功率源,用于补偿PV系统欠缺的功率。BESS系统在0.2 s进入稳态,BESS系统输出功率维持在1.5 kW左右,Pbess=1.5 kW。负载消耗功率等于光伏消耗功率和BESS系统提供的功率之和,根据式(1),净网功率Pnet=0 W,母线电压稳定,得到预期结果。负载电流在0.2 s进入稳态后,PID控制最高波动点iCPL=5.1 A,最低波动点iCPL=4.95 A;SM-ADRC控制最高波动点iCPL=5.07 A,最低波动点为iCPL=4.97 A,稳定在5 A左右,仿真结果与理论运算结果符合。
以上仿真结果的数据见表1,本文所提出的直流微电网SM-ADRC的控制策略在太阳辐射和负载需求都不变的条件下,较传统PID控制对于稳定母线电压振荡,负载电流波动具有更加优越的性能。
4.2.2 光照强度恒定负载功率变化
该条件下,假设太阳光照强度恒定,负载功率变化,且PV系统的输出功率低于负载,须要太阳能光伏单元的DC-DC变换器与BESS的双向DC-DC变换器共同输出功率以满足负载需求。在仿真初始时刻,负载消耗恒定为PCPL=3 kW。0.5 s后负载消耗恒定为PCPL=8 kW,根据欧姆定则,0.5 s前负载电流iCPL=5 A,0.5 s后iCPL=13.33 A。图10为仿真波形。


图10 方案2微电网输出特性Fig.10 Scheme 2 microgrid output characteristic
由图10可见,直流微电网母线电压基本稳定。但PID控制母线电压振荡波动较大,在0.5 s前最高振荡点为619 V,最低振荡点为599 V;在0.5 s后最高振荡点为602 V,最低振荡点为583 V。SM-ADRC控制母线电压0.5 s前最高振荡点为602 V,最低振荡点为596 V;0.5 s后最高振荡点为602 V,最低振荡点为593 V。说明SM-ADRC较PID更稳定,控制效果更好。功率负载在0.2 s进入稳态,负载消耗0.5 s前恒定PCPL=3 kW,0.5 s后恒定PCPL=8 kW。即0.5 s前Pload=3 kW,0.5 s后维持在Pload=8 kW,说明直流微电网系统总功率达到平衡。BESS系统输出功率用来维持母线电压,补偿PV系统欠缺的功率。图中,BESS系统在0.2 s进入稳态,0.5 s前输出功率维持在1.5 kW左右,即Pbess=1.5 W,0.5 s后输出功率维持在6.5 kW左右,即Pbess=6.5 kW。动态过渡时间约为0.02 s,输出功率迅速得到切换。负载功率消耗等于光伏输出功率和BESS系统提供的功率之和。根据式(1),净网功率Pnet=0 W,母线电压稳定,得到预期结果。负载电流在0.2 s进入稳态后,0.5 s前,负载电流iCPL为5 A,0.5 s后负载电流iCPL为13.3 A。SM-ADRC控制比PID控制更加稳定,负载电流波动更小。PID控制负载电流iCPL最高波动点iCPL=5.14 A,最低波动点iCPL=4.97 A;SM-ADRC控制负载电流iCPL最高波动点iCPL=5.06 A,最低波动点iCPL=4.98 A,稳定在5 A左右。从仿真结果看与理论运算结果符合。PID控制负载电流iCPL最高波动点iCPL=13.51 A,最低波动点iCPL=13.01 A;SMADRC控制负载电流iCPL最高波动点iCPL=13.49 A,最低波动点iCPL=13.22 A,稳定在13.33左右,从仿真结果看与理论运算结果符合。方案2的仿真结果数据见表2,3。数据分析说明,本文所提出的直流微电网SM-ADRC控制策略在太阳光照强度恒定,负载需求变化的条件下,对于稳定母线电压振荡和负载电流波动,较传统PID控制具有更加优越的性能。

表2 不同控制算法下,0.2~0.5 s方案2系统稳定性对比Table 2 Scheme 2 between 0.2~0.5 s comparison table of system stability under different control algorithms

表3 不同控制算法下,方案2在0.5 s后系统稳定性对比Table 3 Scheme 2 after 0.5s,comparison table of system stability under different control algorithms
4.2.3 光照强度和负载功率均变化
假设太阳光照强度和负载需求均变化,在仿真初始时,负载消耗恒定为PCPL=3 kW,0.5 s后负载消耗恒定为PCPL=8 kW。根据欧姆定则,0.5 s前负载电流iCPL=5 A,0.5 s后iCPL=13.33 A。0.7 s后太阳光照强度变大,从500 W/m2升至700 W/m2。
图11为仿真波形。
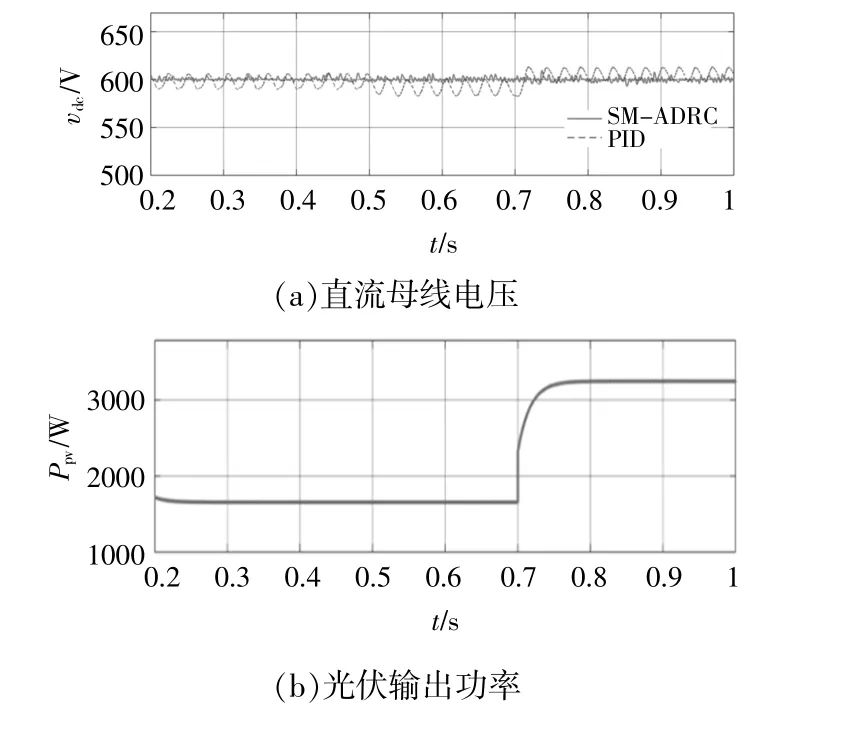

图11 方案3微电网输出特性Fig.11 Scheme 3 microgrid output characteristic
由图11可知,直流微电网母线电压基本稳定。但PID控制母线电压振荡波动较大,在0.2~0.5 s最高振荡点为605 V,最低振荡点为590 V;0.5~0.7 s最高振荡点为601 V,最低振荡点为581 V;0.7 s后电压最高振荡点为616 V,最低振荡点为598 V。SM-ADRC控制母线电压在0.2~0.5 s最高振荡点为602 V,最低振荡点为593 V;0.5~0.7 s最高振荡点为605 V,最低振荡点为597 V;0.7 s后电压最高振荡点为607 V,最低振荡点为598 V。PV系统在0.2 s进入稳态,最大输出功率0.5 s前维持在1.5 kW左右,即Ppv=1.5 kW;0.7 s后维持在3 kW左右,即Ppv=3 kW。动态过渡过程平滑且迅速。整个PV系统输出功率不受直流微电网影响,仅受太阳光照强度和温度的影响。负载功率在0.2 s进入稳态,0.5 s前PCPL=3 kW,0.5 s后PCPL=8 kW。BESS系统功率处于双向流动状态,以维持母线电压,补偿PV系统欠缺的负载功率。BESS系统在0.2 s进入稳态,0.5 s前处于充电状态,功率维持在1.5 kW左右,Pbess=1.5 kW;0.5 s以后处于放电状态,其中,0.5~0.7 s输出功率维持在6.5 kW左右,Pbess=6.5 kW,0.7 s后输出功率维持在5 kW左右,Pbess=5 kW。负载功率消耗等于光伏输出功率和BESS系统提供的功率之和,根据式(1),即净网功率Pnet=0 W。母线电压稳定,得到预期结果。此外,在0.5,0.7 s的过渡过程平滑且迅速。负载电流在0.2 s进入稳态后,0.5 s前,负载电流iCPL为5 A,0.5 s后负载电流iCPL为13.3 A。SMADRC控制较PID控制更加稳定,负载电流波动更小。PID控制负载电流iCPL最高波动点iCPL=5.06 A,最低波动点iCPL=4.92 A;SM-ADRC控制负载电流iCPL最高波动点iCPL=5.05 A,最低波动点iCPL=4.98 A,稳定在5 A左右。PID控制负载电流iCPL最高波动点iCPL=13.42 A,最低波动点iCPL=12.96 A;SM-ADRC控制负载电流iCPL最高波动点iCPL=13.48 A,最低波动点iCPL=13.26 A,稳定在13.33 A左右。PID控制负载电流iCPL最高波动点iCPL=13.62 A,最低波动点iCPL=13.21 A;SM-ADRC控制负载电流iCPL最高波动点iCPL=13.59 A,最低波动点iCPL=13.21 A,稳定在13.33 A左右。仿真结果与理论运算结果符合。
仿真结果的数据见表4~6。

表4 不同控制算法下,方案3在0.2~0.5 s系统稳定性对比Table 4 Comparison table of system stability under different control algorithms

表5 不同控制算法下,方案3在0.5~0.7 s系统稳定性对比Table 5 Comparison table of system stability under different control algorithms(scheme 3,0.5~0.7 s)

表6 不同控制算法下系统稳定性对比表(方案3,0.7 s后)Table 6 Comparison table of system stability under different control algorithms(scheme 3,after 0.7 s)
数据分析说明,本文所提出的直流微电网SM-ADRC的控制策略在太阳光照强度、负载功率同时变化的条件下,对于稳定母线电压振荡和负载电流波,较传统PID控制能更加优越。
5 结论
直流微电网母线电压鲁棒稳定控制是保证供电可靠性的关键。本文分析了光储直流微电网的结构原理与母线电压调节控制。针对光伏发电系统主供电电源,提出改进型变步长扰动观察法对其进行最大功率输出控制;针对BESS系统母线稳压调控需求,提出了SM-ADRC控制方法,并依次设计了TD,SM-ESO和SM-NLSEF 3个控制环节,提高了直流微电网的供电电压稳定性。仿真结果验证了所提方法的正确有效性,与传统的PID控制方法相比,具有更加良好的电压运行调控效果。
