互联电网失步解列过程中的暂态动能变化规律研究

柯贤波，张钢，郑力文，唐晓骏，王吉利，王青

(1.国家电网有限公司西北分部，西安 710048; 2.中国电力科学研究院有限公司 北京100192)

0 引 言

在“双碳”目标下，新能源高占比系统已成为我国电网未来发展的必然趋势。以西北电网为例，截止2020年，西北电网新能源装机容量达到1.24亿千瓦，占比近四成。在此背景下，新能源出力的不确定性，使得典型场景的甄选变得极为困难，制定合理紧急控制方案的难度大大增加，第二道防线防控能力的减弱导致第三道防线压力大幅增加，大规模电力系统功角稳定问题仍是需要关注的重点问题[1]。目前，功角稳定的分析方法主要分为时域仿真法[2-3]、暂态能量函数法[4-7]，以及由此派生出的混合法[8]等。其中，时域仿真法一般通过数值计算先计算出关键变量的动态轨迹，再基于轨迹特征判断系统的稳定性。能量函数法则是通过比较故障清除时刻的暂态能量与临界能量的大小关系判断系统的稳定性。不论采取那种方法，其目的都是预测或者判断系统是否发生功角失稳。对于已经发生失步振荡的电力系统，应尽快实施解列。目前，在解列研究领域，主要分为主动解列[9-11]和失步解列[12-14]两个研究方向。其中，失步解列已广泛应用与工程实际。

电力系统失步解列控制的研究虽已取得很多成果，但还存在一些重要的问题有待研究。例如，当电力系统发生失步时，通常选择在振荡中心处实施解列。但由于新能源的大量接入，会导致阻抗不均甚至等值阻抗发生变化，这些原因均可能引起振荡中心发生漂移[15]。另一方面，大量仿真结果表明，在满足一定的条件下，在振荡中心附近的断面实施解列也可以有效抑制失步振荡。因此，在非振荡中心处解列与在振荡中心处解列之间必然存在某种联系，这种联系尚不明确。又如，以往对暂态能量的研究均是针对未解列的电力系统，文献[16]提出了一种根据发电机自身能量平衡关系来分析暂态能量的方法，文献[1]提出了一种基于支路势能的能量分析方法。这些方法虽然都分析了系统失稳时的能量变化，但均未涉及到解列过程中的暂态能量变化规律。假设电力系统在大扰动的作用下发生两群失步并解列，解列前的系统由于存在大量的暂态能量而不能稳定。而解列后的子系统一般可以快速到达稳定状态，这说明解列后的子系统并不存在大量的暂态能量。也就是说在解列过程中，系统的暂态能量必然发生了较大的改变，目前，对这一过程中暂态能量的变化规律及存在形式还鲜有研究。

因此，研究失步解列过程中暂态能量的变化规律不仅有助于从能量的角度更为深入的认识失步解列过程，还可作为寻找非振荡中心解列与振荡中心解列之间内在联系的一种有效途径，具有重要意义。

鉴于此，本文基于角度中心(Center of Angle, COA)参考坐标，通过选取不同的参考系构造了群间暂态能量和群内暂态能量函数。据此从能量的角度分析了在非振荡中心处解列与在振荡中心处解列之间的联系。

1 群间与群内暂态能量函数

在系统经受大扰动时，假设超前机组属于K群，其余机组属于T-K群，则可将故障清除后其机组间的动态行为划分为群间相对运动和群内相对运动，据此可将全系统的暂态能量分解为群间暂态能量和群内暂态能量。

1.1 全系统的暂态能量函数

对于一个有n台发电机的电力系统，其在COA坐标下的动态方程[4]为:

(1)

扰动发生后，根据多机系统李亚普诺夫能量函数理论。全系统的暂态能量函数[4]可以表示为:

(2)

(3)

1.2 群间暂态能量函数

对于式(1)所示系统，可将其等值为两机系统：

(4)

式中：δ0为系统的角度中心；δK和δT-K为子机群角度中心；θK和θT-K子机群相对于δ0的角度；

由式(4)可得群间暂态能量函数：

(5)

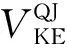
1.3 群内暂态能量函数

对上述系统，当分别以各子机群作为分析对象时，可分别相对于各自的角度中心构造运动方程：

(6)

(7)

式中PKCOA和PT-KCOA分为两个子机群的等值加速功率。

根据式(6)和式(7)可得到子机群的群内暂态能量函数：

(8)

式中 等式右边第一项为暂态动能，其计算公式如下：

(9)

1.4 群间群内暂态能量之和等于全系统暂态能量

将式(5)与式(8)求和，可证得其值等于式(2)所示全系统暂态能量。

2 失步解列过程的暂态能量变化规律

设t0和tc分别为故障时刻和故障清除时刻，tj为发生解列的时刻。遭受大扰动的电力系统在(t0～tc)时段内将被注入大量的暂态能量，暂态能量不守恒；在(tc～tj)时段内，可将电力系统作为一个自治系统来研究，暂态能量守恒[17]。对于这一时间段内暂态能量的变化规律已有大量研究[1,4,17]，不再赘述。因此，本文主要针对解列时刻及解列后的暂态能量变化规律进行研究。

图1 系统解列前后角度中心与θi变化

2.1 群间暂态能量变化规律

对于(t0～tc)时段内的群间暂态能量可采用式(6)求解，不再赘述。当t>tj后，原系统解列为两个独立机群，若此时仍以机群作为分析对象，则有：

(10)

2.2 群内暂态能量变化规律

2.3 总暂态能量变化规律

前文已证明系统的总暂态能量等于群间暂态能量与群内暂态能量之和。由于解列时刻系统的群间暂态能量突降为0，群内暂态能量不变，因此，系统的总暂态能量将在解列时刻突降为群内暂态能量，然后依照群内暂态能量的变化规律变化。

3 在非振荡中心解列与在振荡中心解列的联系

3.1 暂态能量突变对系统稳定性的影响

已有研究指出在故障期间注入的大量暂态能量不能被故障清除后的系统完全消纳是造成系统失稳的原因。

当系统经受大扰动并失稳时，其失稳模式通常表现为两群失稳。此时全系统的暂态能量主要表现为群间暂态能量。根据前文分析，在解列时刻，群间暂态动能突降为0，全系统的暂态能量突变为相对较小的群内暂态能量。群间暂态动能的突然减小使得解列后的系统可以完全吸收剩余的暂态动能使系统到达稳定状态。因此，解列过程中群间暂态能量的突变过程可使系统解列后的暂态稳定性得到较大改善。

值得指出，群间暂态能量的突变规律不仅适用于解列后子系统可以稳定的情形，也适用于解列后子系统不能稳定情形。事实上，对于解列后不能稳定的情形，群间暂态能量的突变同样改善了系统的暂态稳定性，只是改善程度还不足以使其稳定。

3.2 在非振荡中心处解列时暂态能量的变化特点

实际电网运行过程中振荡中心可能漂移至相邻线路甚至区域电网内部，而漂移后的振荡中心所在线路不一定装设解列装置，此时不得不在安装解列装置的非振荡中心处实施解列。因此，有必要对在非振荡中心处解列的情况进行分析。

众所周知，电力系统解列必须满足同调约束条件，而同调机群的分群结果仅与发电机转子的相对位置有关，与解列位置的选取方式无关。因此，在满足同调约束的前提下，无论在非振荡中心处解列还是在振荡中心处解列其等值两机系统的运动方程相同，故二者的群间暂态能量变化规律相同。根据上节分析结果可知，在非振荡中心处解列与在振荡中心处解列将具有相近的解列效果。

需要指出，解列断面的选取会影响到系统的负荷分配，负荷分配方式的不同会影响解列后系统的稳定性，因此，假设在非振荡中心处解列与在振荡中心处解列时负荷分配变化不大。

4 算例分析

4.1 IEEE 39节点系统算例

IEEE 39节点系统结构如图2所示。假设线路16-17发生持续0.2 s的三相短路故障，通过时域仿真可知，振荡中心所在断面为(线路1-2、8-9)，并且线路两侧电压相角差在0.88 s时超过180°。假设断面(线路1-2、8-9)为断面I，选择0.9 s在断面I实施解列，该过程的发电机相对功角曲线如图3所示。

图2 IEEE 39节点系统

图3 发电机相对功角

由图3可知，故障后原系统发生失步，机群K仅包含一台发电机G1，其余机组属于T-K群。原系统解列后，机群K直接到达同步稳定状态，机群T-K内部机组间功角再经历短时的减幅振荡后同样到达同步稳定状态。根据公式(2)、(6)、(10)计算解列过程中的暂态能量变化示于图4。

由图4(a)可以看出，故障清除后全系统的暂态动能转化为暂态势能，总暂态能量守恒。至解列时刻全系统的暂态动能发生突变，总暂态能量的标幺值由15突降至2附近，随后，全系统暂态动能逐渐下降为零，系统到达稳定状态。比较图4(a)和图4(b)可知，全系统总暂态能量和群间与群内暂态能量之和的变化规律几乎完全相同，说明可以将系统总暂态能量分解为群间暂态能量与群内暂态能量进行研究。观察图4(c)，可以看出群间暂态能量在解列时刻由解列前一个很大值突变为零后保持不变；从图4(d)可以看出群内暂态能量在解列时刻不会发生突变，且解列后很快到达稳定状态。

图4 在断面I处解列时的暂态能量变化

值得指出，暂态能量函数是一种通过对系统的转子运动方程进行积分而得到的数学方程，其虽名曰“能量”，但实际上是通过数学方法构造出来的函数值，并不是电力工程中的明确物理量。因此，暂态能量在表述中一般采用无量纲的表达形式。因此，在例如公式(2)等暂态能量的计算过程中，将式中机械功率、电磁功率等物理量均根据系统基准容量100 MV·A进行折算，因此，算例中的各类暂态能量值均是以系统基准容量进行折算后的标幺值。后续算例中延用了这一折算方法。

分析以上暂态能量的变化规律可知，解列前原系统因为无法消纳全部的暂态能量而失稳，解列时刻，全系统的暂态能量由于群间暂态能量的突降而大幅下降，解列后的系统能够消纳剩余的暂态能量从而到达稳定状态。因此，解列过程中群间暂态能量的突变是使系统解列后的暂态稳定性能够得到较大改善的重要原因,验证了前文所述结果。

下面分析在非振荡中心处解列时的暂态能量变化特点，假设系统发生故障及切除时间等情况均与前述相同，仅将解列断面选择为振荡中心相邻断面(line1-2、line5-8、line7-8)，设为断面II。

从图5可以看出在断面II解列时，群间暂态能量同样占全系统暂态能量的绝大多数，其变化特点与在断面I解列时相同，与前文理论分析结果相一致。在断面II解列时的功角曲线如图6所示。可以看出其解列效果与在断面I解列时基本一致。

图6 发电机相对功角

4.2 某区域电网模型

采用我国某区域互联电网模型进行研究。其中区域A与区域B之间的网间联络线如图7所示。现假设区域B内部某双回线路中的一条发生持续1 s的三相短路故障(假设故障处理不及时)。根据时域仿真，在0.76 s和1.07 s时故障点附近分别有一台发电机相对于全网失步；图7中线路L3在2.66 s时两侧电压相角差超过180°，区域B与区域A发生失步。

图7 区域B与区域A联络断面

4.2.1 在振荡中心处解列

选择失步后10个周波(0.2 s)作为解列时机。故在0.96 s和1.27 s时分别解列两失步机组，在2.86 s时解列区域B与区域A。解列断面I选择图3中振荡中心所在线路L3。由于区域B因切机造成大量功率缺额，故解列后切除区域B内部一定量负荷。全过程的功角曲线如图8所示。

由图8(a)和8(b)可知，系统故障后，先后有两台机组相对于全网失步并解列，随后区域B与区域A发生两群失步并解列。解列后两个子系统很快到达稳定状态。

根据式(2)，计算故障清除后全系统的暂态能量曲线如图9所示。

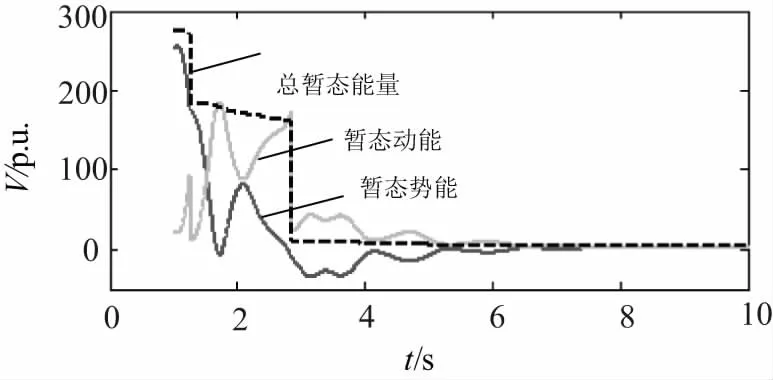
图9 全系统暂态能量

观察图9，故障清除后全系统的暂态动能转化为暂态势能，总暂态能量基本保持不变，仅由于调速器及阻尼作用略有降低；至第二次解列失步的单台发电机时，全系统的暂态动能发生第一次突变，总暂态能量值由275突变至185，随后暂态动能与暂态势能再次发生相互转化。忽略调速及阻尼影响，可近似认为该过程中总暂态能量保持不变；至2.86 s，区域B与区域A因失步而解列，全系统的暂态动能再次发生突变，总暂态能量由160突降至10附近，随后，全系统暂态动能逐渐下降为零，系统到达稳定状态。可以看出，解列时刻暂态能量的突降是使失步系统能够到达同步稳定状态的重要原因。

依据式(4)、式(10)计算群间暂态能量和群内暂态能量并计算二者之和，结果如图10所示。

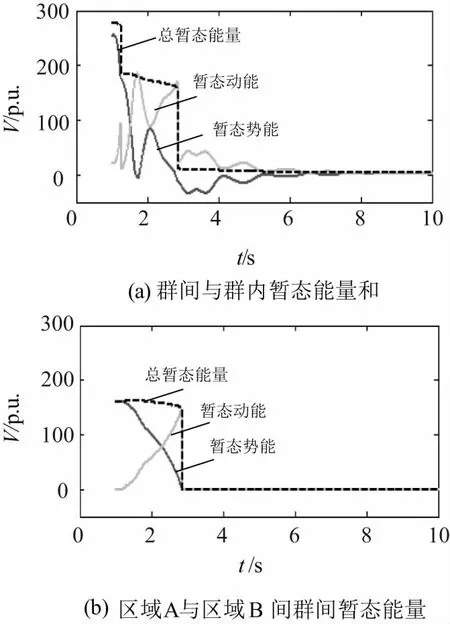
图10 在断面I解列时的暂态能量变化

比较图10(a)与图9，可以看出两图中曲线变化规律完全相同，证明全系统暂态能量可分解为群间与群内暂态能量进行分析。

观察图10(b)，可以看出故障清除后，系统的群间暂态势能不断转化为群间暂态动能，这一过程中，总暂态能量基本保持不变。至解列时刻，群间暂态势能下降至0，群间暂态动能突降为0，系统的总群间暂态能量突降为0；观察图10(c)和图10(d)，在最后一次解列失步的单台发电机后，两子系统的群内暂态能量均由一个较小的值逐渐衰减为0。并且群内暂态能量在两机群解列的时刻不发生突变。说明仿真结果与前述理论分析结果一致。

比较群内暂态能量与群间暂态能量，易看出在解列时刻群内暂态能量的值相对于群间暂态能量的值较小，说明此时系统的暂态能量主要表现为群间暂态能量。这也说明解列时刻群间暂态能量的突变过程是使得失步系统解列后暂态稳定性得到较大改善的重要原因。

4.2.2 在非振荡中心处解列

假设故障类型、故障清除时间等因素不变，将解列断面选择为图3所示的解列断面II。

在解列断面II解列时的暂态能量变化如图11所示。

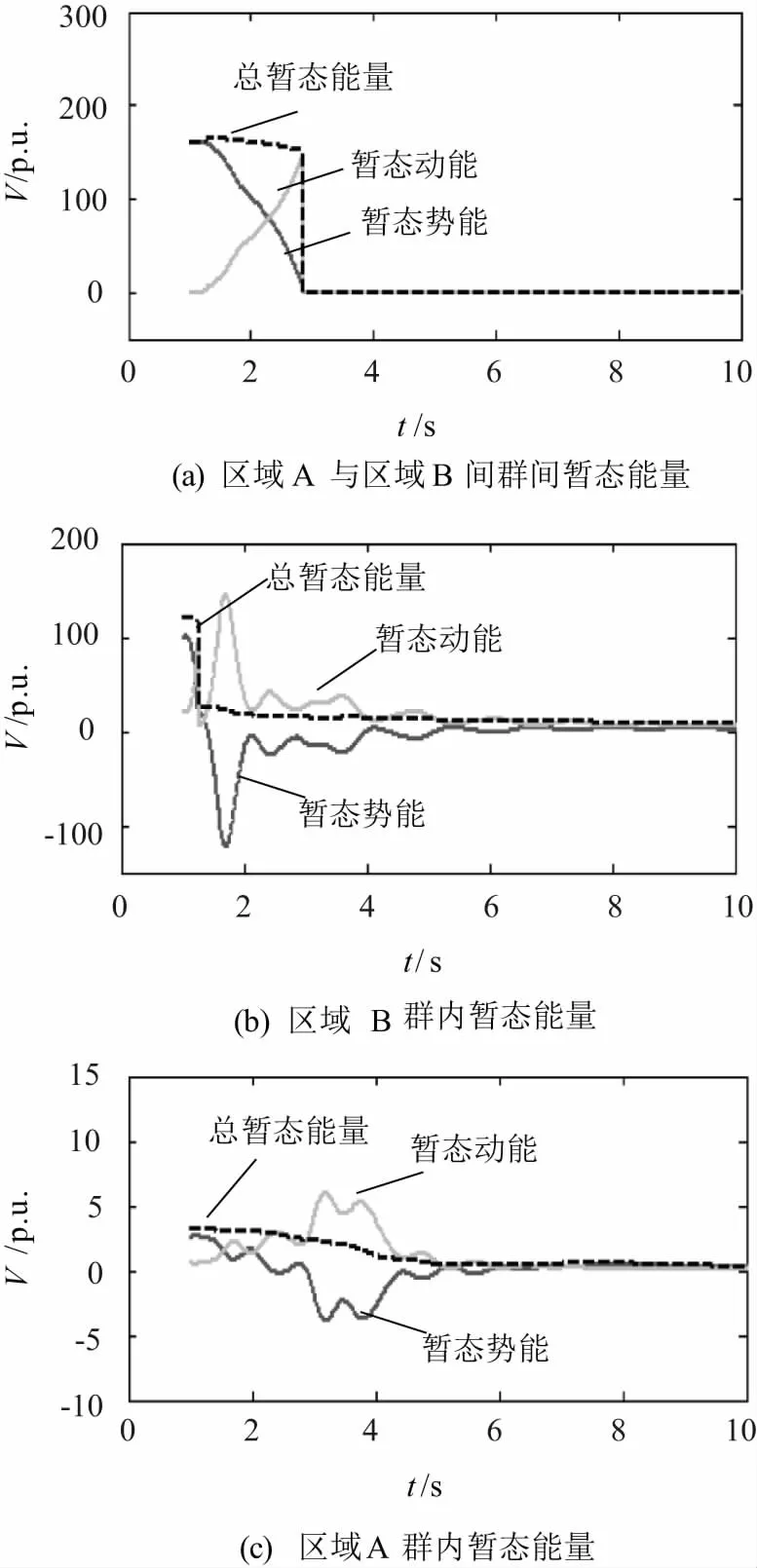
图11 在断面II解列时的暂态能量变化

对比图11(a)和图10(b)，可以明显看出在两个不同断面解列所引起的群间暂态能量变化规律相同；分别对比图11(b)和图10(c)、图11(c)和图10(d)可知，在原系统解列前群内暂态能量具有相同的变化规律，在解列为两个子系统后，两子系统同样很快到达稳定状态。根据前述理论分析结果，由于在解列时刻，作为系统主要暂态能量的群间暂态能量具有相同的变化规律，且系统在两种情况下的负荷分配方式变化不大，可以推断在断面II解列与在断面I解列具有相近的解列效果。为了验证这一推断，现将在断面II解列时的功角变化曲线示于图12。观察图12可知，系统解列后同样分为区域B与区域A两个机群，解列后的两个子系统同样快速到达稳定状态。证明前述推断正确。

图12 在断面II解列时的功角曲线

5 结束语

本文通过分析电力系统失步解列过程中暂态能量的变化规律，得到以下结论：

(1)在新型电力系统中，受高比例新能源接入影响，振荡中心易发生漂移。在这一场景下，传统根据振荡中心交流电气量特征构造的解列判据可能存在不适应的情况，解列装置可能无法正确动作，这会对大电网造成极大危害，甚至引发大面积停电事故。本文研究成果指出在负荷变化不大的情况下，在非振荡中心处解列与在振荡中心处解列具有相同的暂态能量突变规律，即具有相同的解列效果。依据这一结论，工程人员可根据暂态能量的突变规律选取更适合的解列断面。例如，某些省间断面虽然不是振荡中心，但断面清晰，当根据本文提出的方法计算得出在这些断面解列具有相同的能量特征时，可将其作为实际的解列断面，这将大幅降低失步解列难度。具有较强的工程指导意义；

(2)在大扰动下，系统的暂态能量可以分解为群间暂态能量和群内暂态能量。在解列时刻，失步机群间的群间暂态能量突降为0，群内暂态能量不变，全系统的暂态能量突降为群内暂态能量；

(3)解列时群间暂态能量的突降实际上是由群间暂态动能突变为同步动能引起的。该突变过程是使失步系统解列后的暂态稳定性得到较大改善的重要原因之一；

(4)当系统在扰动后的失稳模式表现为较为理想的两群失稳时，解列后K群和T-K群的群内暂态能量值通常很小，子系统能够快速到达稳定状态；而当原系统的失稳模式为不太理想的两群失稳时，此时K群和T-K群的群内暂态能量可能存在较大的情况，甚至导致相继失稳，此时通常需要快速解列失步系统。