基于迭代加权改进BP神经网络的电容式电压互感器变比幅频特性拟合方法

代双寅，李琼林，唐旭，刘开培

(1.国网河南省电力有限公司电力科学研究院，郑州 450052； 2.武汉大学 电气与自动化学院，武汉 430072)

0 引 言

随着新能源发电、高压/特高压直流输电等基于电力电子技术的装置和系统在电力系统中应用的日益广泛，迫切要求实时掌握高电压系统中的谐波状况，为制定针对性控制和治理措施提供真实可靠的依据。

电容式电压互感器(CVT)被广泛应用于中性点直接接地的高压系统中，为计量、监控和保护等二次系统提供高精度的工频电压信号[1-4]。但在谐波条件下，CVT电路内部工频条件下的谐振状态被破坏，其变比频率响应特性在宽频带范围内并非常数[5-7]，采用标称变比计算高压侧谐波电压将导致很大的误差，电容式电压互感器国家标准中也明确规定：“电容式电压互感器不能被用于谐波测量的场合”[8]。

目前对CVT谐波测量误差的原理和定性分析的研究开展较多。文献[9]讨论了CVT谐波电压测量存在的问题，进行了测量误差来源机理的分析；文献[10]通过建立具有谐振型阻尼器CVT的谐波等效电路，分析了二次侧负载和阻尼器等对CVT谐波测量精度的影响；文献[11-12]分别从系统传递函数和变比幅频特性的角度出发，分析了杂散电容和耦合电容对CVT谐波测量误差的影响；文献[13]研究了中间变压器励磁阻抗与分压电容对CVT变比的影响；文献[14]对谐波条件下CVT测量误差的试验方法进行了研究，给出了合理有效的测量误差研究试验方案。尽管采用电阻/电容分压器可获得高精度谐波电压测量结果，但这些专门用途的设备体积大，价格昂贵[15]；文献[16-17]提出了基于交直流滤波器的直流输电系统谐波电压测量方法，分析了元件失谐对于谐波测量精度的影响。尽管该方法简单易行，但只能应用于具有滤波器的高压系统谐波电压测量；文献[18-19]提出了在CVT的支路中增加电流互感器，利用测量得到的电流计算CVT高压侧谐波电压的方案，该方法需要对CVT内部电路进行改造。

目前，CVT仍是高电压系统应用最为广泛的电压测量设备，研究更具实用性的谐波测量误差校正方法，提供相对准确可靠的谐波电压测量结果具有重要的现实意义和实用价值。由于CVT的变比在宽频范围内并非常数，其变比幅频特性为一复杂曲线，从而CVT无法通过标称变比(即工频下的变比)来准确测量谐波电压值。但通过拟合该变比幅频特性曲线可以获知各频率下CVT的变比值，进而可以对CVT的谐波测量结果进行校正，获得准确的谐波电压值[20]；文献[21-24]研究了通过神经网络对CVT变比幅频特性曲线进行拟合，进而修正谐波电压测量值。但是由于CVT变比幅频特性曲线在所关注频带范围内具有极大值与极小值，且在极值点附近变化率很大，当采用BP神经网络对该曲线进行拟合时，只能保证拟合曲线与已知数据点间的均方误差满足收敛条件，可能出现在极值点附近拟合误差较大的情况，即通过拟合得到的某些频率点的变比与真实变比之间的偏差较大，不利于反映这些频率对应的高压侧谐波电压的真实值。

文中针对这一问题，提出了采用迭代加权改进的BP神经网络对变比幅频特性曲线进行拟合。该方法在保证已知数据点与拟合曲线间的均方误差满足收敛条件的同时，可以进一步降低拟合曲线与已知数据点之间的最大误差。使用该方法对CVT变比幅频特性曲线进行拟合后，基于所得拟合曲线便可以得知在各个频率下CVT的变比值，从而校正CVT的谐波电压测量结果，获得准确的谐波电压值。

1 CVT宽频等效电路及其幅频特性曲线

1.1 CVT宽频等效电路

CVT由电容分压器(由高压电容C1和中压电容C2组成)、电磁单元(由补偿电抗器LC、中间变压器T和阻尼器Zf组成)、负载(由测量绕组负载Z1和保护绕组负载Z2组成)、保护间隙N、载频漏线圈Ld和避雷器A等部分，如图1所示。

在工频条件下，补偿电抗器与分压电容器发生串联谐振，使得CVT工频下表现出恒压源形式，二次输出电压不受负载大小的影响，该原理可由从图1中的M点往左看入的戴维南等效电路解释，等效电路如图2所示。

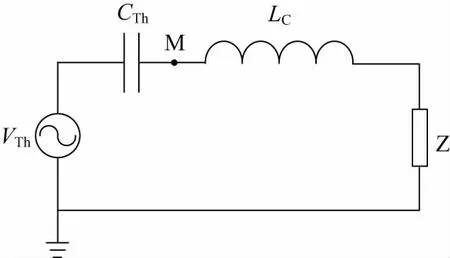
图2 工频条件下CVT戴维南等效电路

图2中电容CTh为高压电容C1与中压电容C2的并联等效电容；VTh为CVT一次侧的高压经电容C1与C2分压后的电压值(VTh=V1C1/(C1+C2))；LC为补偿电抗器；Z为等效负载阻抗。在工频条件下，等效电容CTh与补偿电抗器L发生串联谐振，使得负载Z上的电压值恒等于VTh，不受负载大小的影响。

当CVT所测量的电压中含有谐波时，在对应谐波频率下，CVT中的串联谐振条件被破坏，且在高频时CVT中的杂散电容不可忽略，导致了CVT在谐波条件下的变比不等于标称变比(即基波条件下的变比)，其变比幅频特性曲线在一个较宽频带范围内为一复杂曲线，因此CVT无法基于标称变比测量谐波电压。

下面以某400 kV具有速饱和型阻尼器的CVT为例，通过分析其宽频等效电路获得相应的变比幅频特性曲线。图3给出了该CVT折算至一次侧的宽频等效电路，主要由电容分压器、补偿电器、中间变压器和阻尼器的谐波等效电路构成，负载由串联的Lz和Rz表示。文献[5]给出了谐波等效电路元件参数的获取方法。其具体参数如表1所示。

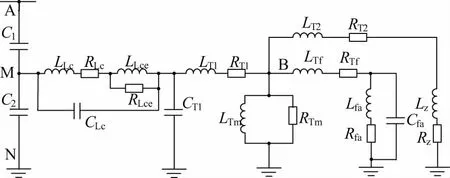
图3 CVT宽频等效电路

表1 CVT参数

1.2 变比幅频特性曲线

图4给出了通过仿真得到的该CVT变比标幺值(以工频变比为基准值)的幅频特性曲线，所得变比幅频特性曲线与文献[5]中的一致。

图4中的变比幅频特性曲线表明，CVT的变比随着频率变化而改变，导致CVT无法通过标称变比来准确测量谐波电压。此外，该曲线具有多个极大值与极小值，且在极值点附近变化率非常大。

图4 速饱和型阻尼器CVT变比幅频特性

对图4所示曲线进行拟合可以得到各个频率下CVT的变比值，基于该变比值可以对CVT的谐波电压测量结果进行校正：

(1)

式中U′为某一频率下CVT的谐波电压测量值(基于标称变比)；U为该频率下CVT高压侧谐波电压真实值；kN为CVT的标称变比；k为基于变比曲线拟合得到的该频率下CVT的变比值。

图5展示了采用BP神经网络对图4所示CVT变比幅频特性曲线的拟合结果。在图4所示变比幅频特性曲线中的1～2 500 Hz频带范围内，每隔5 Hz取一组频率及其对应的变比值作为一个训练样本，共取501个样本作为神经网络的训练集。所使用的神经网络包含输入层、隐藏层和输出层；输入层为单神经元，以频率作为输入，隐藏层含有100个神经元，输出层含一个神经元，以CVT在输入频率下对应的变比作为输出。以神经网络的预测均方误差(MSE)小于0.000 5作为收敛条件。

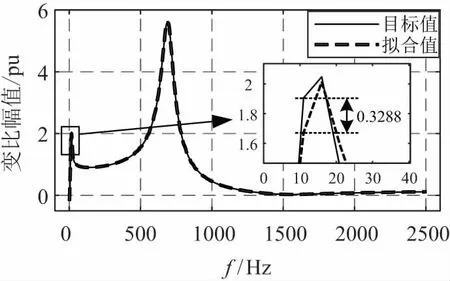
图5 拟合结果

从图5所示结果可以看出，神经网络对变比幅频特性曲线的整体拟合情况较好。这是由于神经网络的目标函数为预测误差的均方值，如式(2)所示[25]。

(2)

式中M为样本总数；tm与ym分别为第m个样本的目标值与预测值。

以式(2)为目标函数可使所得到的拟合曲线与已知数据点之间的均方误差满足收敛条件，但在变化率很大的极值点附近拟合效果较差。从图5中可以看到在曲线的第一个极值点附近，最大误差达0.328 8。由式(1)可知，由曲线拟合得到的各频率下的变比值直接影响谐波测量的精度。因此在以测量谐波为目的的曲线拟合过程中，不仅希望整体拟合效果较好，更希望所得的拟合曲线在最大误差点的误差尽可能小，提高在各个频率点的测量精度。

2 迭代加权改进BP神经网络

为了使BP神经网络在CVT变比幅频特性曲线拟合中的最大误差点的误差尽可能小，提出了使用迭代加权方式改进的BP神经网络拟合方法，该方法采用迭代加权的方式对BP神经网络拟合误差最大的点进行加权，使得在满足神经网络原有收敛条件下，拟合曲线的最大误差随着迭代过程的进行逐渐降低。迭代加权改进的BP神经网络拟合方法的流程图见图6。迭代加权改进BP神经网络的算法流程如下。

(1)初始化迭代次数与各样本的权重系数：

i=1

(3)

Wm=1 (m=1,2,…,M)

(4)

式(4)中Wm代表第m个样本的权重系数；M为样本总数。

(2)对样本输入值进行加权：

(5)

式(5)中xm表示第m个样本输入值；xm′表示加权后的样本输入值。

(3)将加权后的样本输入值xm′与样本目标值tm组成新的样本，形成新的训练集。

(4)将新的训练集输入至BP神经网络中进行训练。

(5)将未经加权的样本输入值xm输入至训练后的神经网络中，得到预测值ym，计算各样本的预测误差绝对值，并找出最大误差emax：

(6)

(6)判断迭代次数i是否达到预先设定的迭代次数上限或最大样本预测误差绝对值emax是否满足要求，若i达到上限或emax满足要求则结束迭代，否则进入第(7)步。

(7)更新具有最大误差的样本(设第n个样本的拟合误差最大)对应的权重系数Wn：

Wn=Wn+f(emax)

(7)

式中f(·)的取法没有限制，只要使得f(emax)足够小，保证迭代收敛即可。

(8)更新迭代次数：

i=i+1

(8)

(9)返回第(2)步，开始下一次迭代。

图6 迭代加权改进BP神经网络流程图

为了体现所提出的迭代加权改进BP神经网络在降低拟合曲线最大误差方面的优势，采用迭代加权改进BP神经网络对图4所示CVT的变比幅频特性曲线进行拟合，所采用的训练集以及BP神经网络的参数设置均与文中1.2节中BP神经网络一致。拟合结果以及最大拟合误差随迭代次数变化情况如图7与图8所示。

图7 拟合结果

图8 最大误差变化情况

从图7与图8可见，在使用迭代加权改进BP神经网络后，随着迭代次数增加，变比幅频特性曲线的最大拟合误差从仅使用BP神经网络的0.328 8降低至0.248 4，降幅达24.45%，有效降低了极值点附近的最大拟合误差，提升了通过BP神经网络拟合变比幅频特性曲线这一方式测量谐波的精度。

图9给出了采用迭代加权改进BP神经网络与仅使用BP神经网络两种拟合方式下各频率点对应的变比拟合误差对比情况。

从图9所示的对比情况可见，与仅采用BP神经网络进行拟合时相比，采用迭代加权改进的BP神经网络在进行变比幅频特性拟合时可以在几乎不增大其余频率点拟合误差的情况下有效降低最大拟合误差，即采用该方式拟合所得变比幅频特性曲线不仅能够保证拟合曲线的均方误差不高于仅采用BP神经网络时的情况，与之相比还能进一步降低最大误差点的拟合误差。

图9 拟合误差对比

最后，在文中采用仿真数据作为样本只是作为算例，对所提出拟合方法的有效性进行验证。在工程应用中，可以对有谐波测量需求的CVT进行试验，事先选取某些合适的频率点，测量CVT在这些频率点下的变比值，获得BP神经网络所需的训练样本数据。这样可以避免通过CVT宽频等效模型所得的变比样本数据与实际CVT变比数据有差异的问题。最后再利用文中所提出的迭代加权改进BP神经网络拟合方法对CVT的变比幅频特性曲线进行拟合，得到最大误差较小的变比幅频特性拟合曲线，提高谐波测量的精度。

3 结束语

通过BP神经网络拟合CVT变比幅频特性曲线可以实现谐波测量。但对于CVT变比幅频特性变化率非常大的曲线，在仅使用BP神经网络对其进行拟合时，只能保证所得拟合曲线与已知数据点之间的均方误差满足收敛条件，而可能有某些数据点与拟合曲线之间的偏差较大的情况出现。针对这一问题，文中提出了使用迭代加权改进BP神经网络对幅频特性曲线进行拟合。使用该方法不仅能够使得拟合曲线与已知数据点之间的均方误差满足收敛条件，还可以有效降低拟合曲线的最大误差，有益于提高所关注的全频带范围内的拟合精度。