基于改进自适应构造区间法的电力负荷区间预测
2022-11-23陆臣斌包哲静于淼蔡昌春
陆臣斌,包哲静,于淼,蔡昌春
(1.浙江大学 工程师学院,杭州 310015; 2.浙江大学 电气工程学院,杭州 310027;3.河海大学 物联网工程学院,江苏 常州 213022)
0 引 言
准确的电力负荷预测在现代电力系统经济和安全运行中至关重要。近年来,在能源互联网的大背景下[1],负荷影响因素更加多元化,负荷特性也呈现出新的特点和趋势[2]。同时,电力系统高效经济运行对负荷预测精度的要求逐步提高,传统的点预测方法越来越难以满足实际需求。负荷区间预测能够量化预测结果的不确定,可以给电力工作人员带来更多的参考信息,有利于制定各种科学合理的策略,因而越来越受到重视。
广泛用于电力负荷区间预测的方法主要包括统计方法、人工智能方法和混合方法[2]。基于时间序列的统计模型,如:自回归、指数平和差分整合移动平均自回归模型可以分解历史数据中的长期趋势,并将历史趋势推演到未来[2-5]。因此,这些方法需要大量的过去数据来进行模型开发[5]。与上述方法相比,许多研究提出了直接产生预测区间上下界的人工智能方法[6-11]。这些方法基于各种机器学习模型,如人工神经网络、支持向量机和核极限学习机方法[6-9],并利用各类启发式算法对参数进行优化,如模拟退火和粒子群优化算法[10-11]。在以往的研究中[12-14],采用基于区间覆盖概率(Prediction Interval Coverage Probability,PICP)和区间平均宽度(Prediction Interval Normalized Average Width,PINAW)的双目标优化预测方法,可以得到最优的预测区间。然而,在帕累托前沿的众多非支配解中平衡这两个目标是非常困难的[15]。因此,为了解决这个问题,在后续相关研究中,有使用覆盖宽度标准(Coverage Width Criterion,CWC)指标将双目标优化问题转化为单目标优化问题[15-17],这些方法被称为基于上下界估计(Lower Upper Bound Estimation,LUBE)的方法。随着优化参数的增加,启发式算法往往需要较长的搜索时间。因此,这些方法仅限于应用在参数相对较少的浅层机器学习模型。
深度学习已成为近年来的研究热点,更复杂结构的神经网络具有更强的非线性映射能力,并且可以从数据中提取比传统机器学习模型更多的内在特征[18]。代表性的深度学习模型包括卷积神经网络、堆叠式自动编码器和长短期记忆神经网络(Long and Short-Term Memory,LSTM)[19-21]。近年来,门控循环单元(Gate Recurrent Unit,GRU)被开发出,作为具有简化门控机制的LSTM的扩展,具有与LSTM类似的性能以及较低的计算负担[22]。但这些模型很少应用于区间预测问题。基于以往的研究,文献[23]提出了一种具有高学习能力的GRU预测模型,可以直接生成预测区间,并采用高效的梯度下降算法进行模型训练,如均方根传递(Root Mean Square Prop,RMSProp)和自适应动量(Adaptive momentum,Adam)算法[24-25]。基于梯度的性质,这些算法需要可微的代价函数进行监督学习,故其不能对CWC这类不可微的评估指标进行优化[7]。为了解决这个问题,文献[23]提出了一种基于构造区间的自适应优化方法,为模型的监督学习建立高质量的训练标签。但该方法在应用时并未考虑预测区间宽度的优化,且每次训练得到的预测区间具有较大不确定性。
文章对基于构造区间的自适应优化方法加以改进,在优化过程中引入区间平均宽度,采用基于PID思想的闭环自适应调节策略提高了预测效果,同时应用验证集的训练指标选出最好的训练模型,提高了预测的稳定性。下面先介绍区间预测评估指标,基于GRU的区间预测模型以及基于构造区间的自适应优化方法,再以澳大利亚新南威尔士AEMO(2006年~2010年)及欧洲阿尔巴尼亚(2017年~2019年)的历史负荷数据为例进行对比,验证改进的效果。
1 算法实现
1.1 门控循环神经网络(GRU)
近年来,GRU被广泛应用于处理时间序列数据。作为LSTM的改进版,GRU通过放弃记忆细胞并引入更新门来替换输入门和遗忘门,简化了LSTM结构。许多研究表明,GRU与LSTM具有相似的性能,但其计算量更少。GRU的结构单元如图1所示。
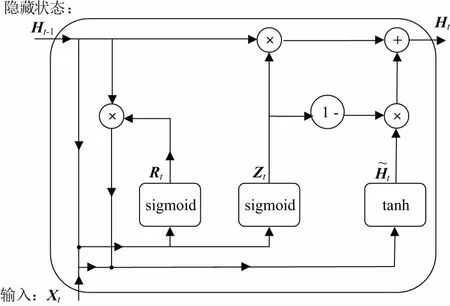
图1 GRU结构单元
对于某一时间步t,假设输入为小批量样本Xt∈Rn×d,其中n为样本个数,d为样本维数,上一个时间步的隐藏状态为Ht-1∈Rn×h,h为隐藏单元个数。重置门Rt∈Rn×h和更新门Zt∈Rn×h的计算如下:
Rt=σ(XtWxr+Ht-1Whr+br)
(1)
Zt=σ(XtWxz+Ht-1Whz+bz)
(2)
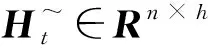
(3)
式中Wxh∈Rd×h和Whh∈Rh×h是权重参数矩阵;bh∈Rl×h是偏差参数矩阵,采用tanh()激活函数将候选隐藏状态的值保持在区间(-1,1)中。从式(3)可以看出,重置门通过控制上一时间步的隐藏状态矩阵来影响当前时间步的候选隐藏状态,可以选择性得丢弃和保留历史信息。
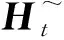
(4)
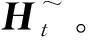
1.2 基于GRU的区间预测模型
为了将最先进的深度学习技术引入负荷区间预测,构建了一个多层神经网络模型,如图2所示。
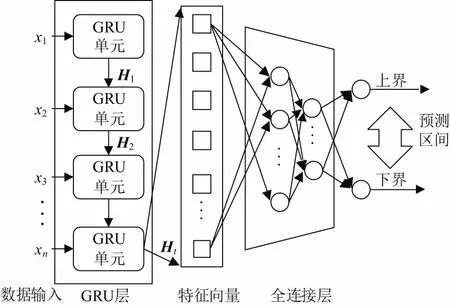
图2 GRU区间预测结构
在该模型中,GRU输入层用于时间序列的特征提取,再通过全连接层对特征进一步处理,输出预测区间上下界。具体解释如下:第一层为GRU循环输入层,基于输入序列x={x1,…,xn}完成特征向量Ht的提取,时间序列长度为n,其中每个xi为第i时刻的负荷值,最后一个GRU单元的输出为提取的特征向量,输入至其后的全连接层。全连接层主要由几个隐藏层和一个输出层组成,输出层包括两个神经元,分别输出预测区间的上界和下界。激活函数的作用是提供规模化的非线性化能力,文中采取ReLU作为全连接层后的激活函数,如式(5)所示,可以有效缓解梯度消失的问题,并且加快收敛速度。
(5)
1.3 区间预测评估指标
区间预测评估结果可以用区间覆盖率(PICP)和区间平均宽度(PINAW)来描述。其中,在同一置信度(Prediction Interval Nominal Confidence,PINC)下,PICP值越大,同时PINAW值越小,表明模型的性能越好[26],其定义如下:
(6)
(7)
(8)
式中n为测试集样本的个数;Ui、Li分别为生成的区间上下限;yi为第i个样本的观测值,观测值在区间内时为1,否则为0;R表示测试集的范围,用于对该指标进行归一化。
为了综合考虑区间宽度和覆盖率,引入基于PICP和PINAW的综合指标CWC作为评价标准,其定义如下:
CWC=PINAW(1+γe-ηPICP-μ)
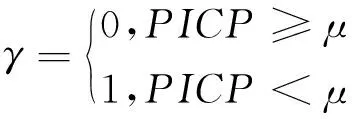
(9)
式中μ是由置信度决定的;η为惩罚系数,当区间覆盖率小于给定置信度时,给予指数级的惩罚,当覆盖率大于置信度时,只考虑区间平均宽度PINAW;综合指标CWC值越小,代表预测结果越好。
1.4 基于构造区间的自适应优化方法及其改进
1.4.1 基于构造区间的自适应优化方法
该方法是文献[23]提出的,其中采用了一种结合了自适应学习策略和动量机制的梯度下算法Adam来训练预测模型,该算法可以加快收敛速度,并有效的避免陷入局部最优[25]。Adam在本质上是基于反向传播算法的,因此必须构造一个可导的代价函数来实现有监督学习。为了定义这样的代价函数,训练标签是必须的。故文中针对给定的区间预测置信度PINC,通过人工构造上下界的方法直接获得训练标签[23]。对于训练集中一系列训练标签Y=[y1,y2,…,yn],其中n是训练集样本数,构造区间定义如下:
(10)
式中Yu和Yl分别是构造区间的上界和下界;du、dl是构造区间的上下宽度,作为自适应优化的变量,由此可构建基于均方误差的代价函数:
(11)
式中Ui、Li分别是模型的第i个输出上界和下界,因为每个训练样本的fcost可导,因此Adam算法可以使用该函数来计算神经网络中每个权重和偏差的梯度。
问题转化为寻找合适的上下宽度du、dl进行训练,针对梯度下降算法不能像柔性启发式算法那样优化宽度的问题,提出了一种自适应宽度优化方法。在每个训练周期之后,模型输出的预测区间将逐渐接近构建的训练区间,并且两者之间会产生拟合误差。平均拟合误差定义如下:
(12)
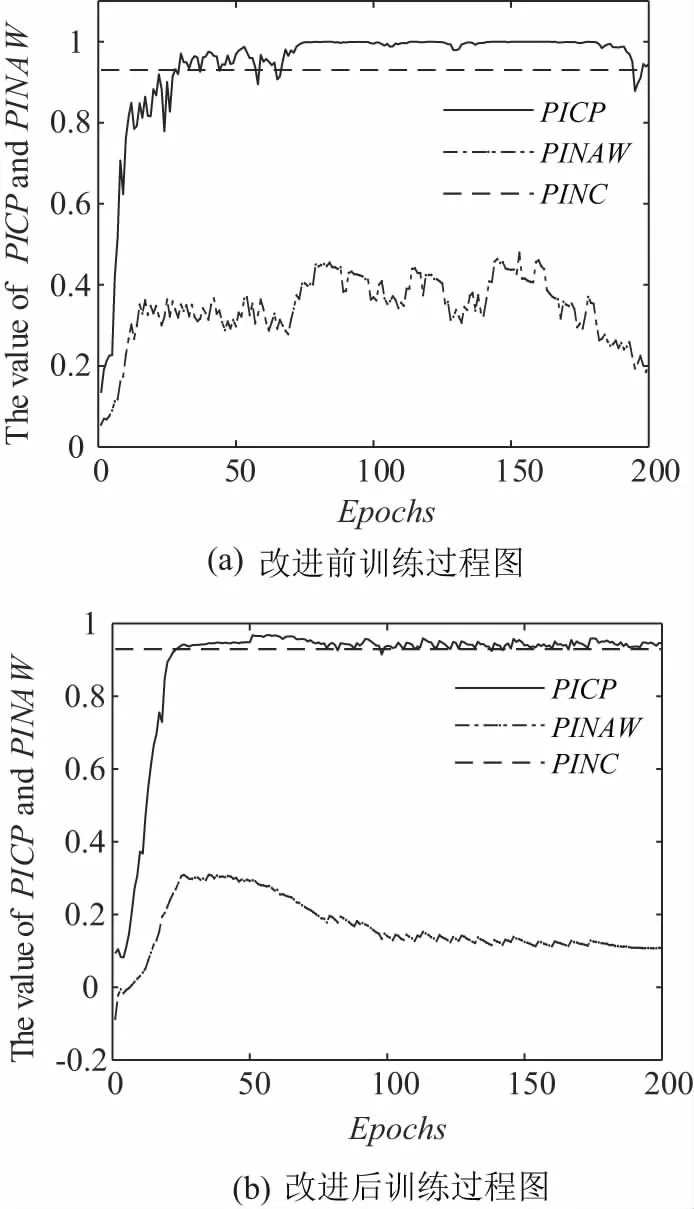
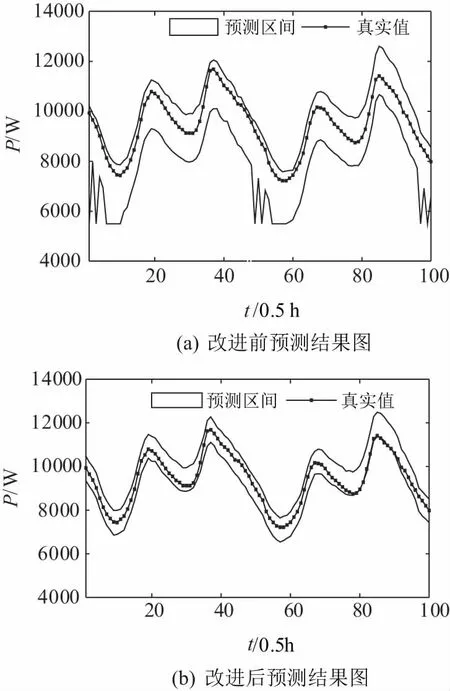
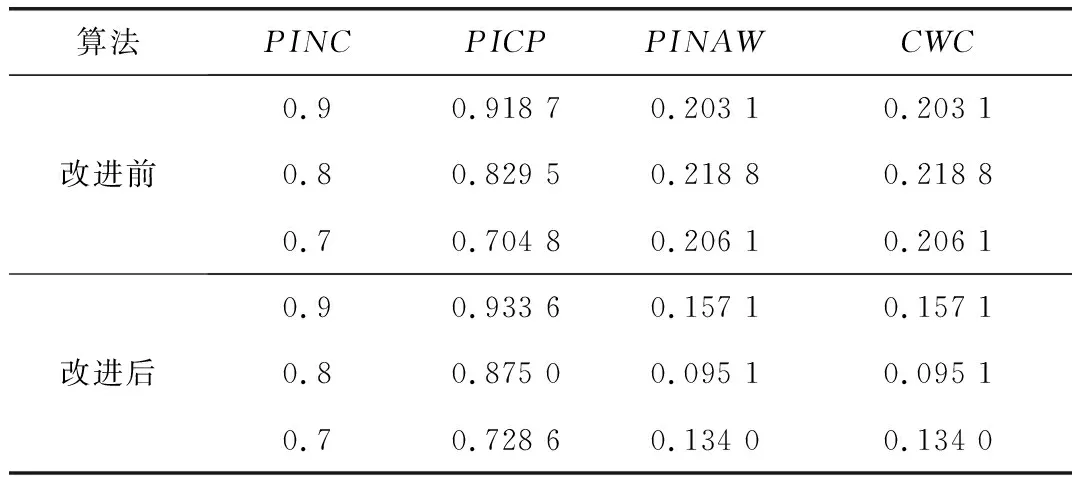
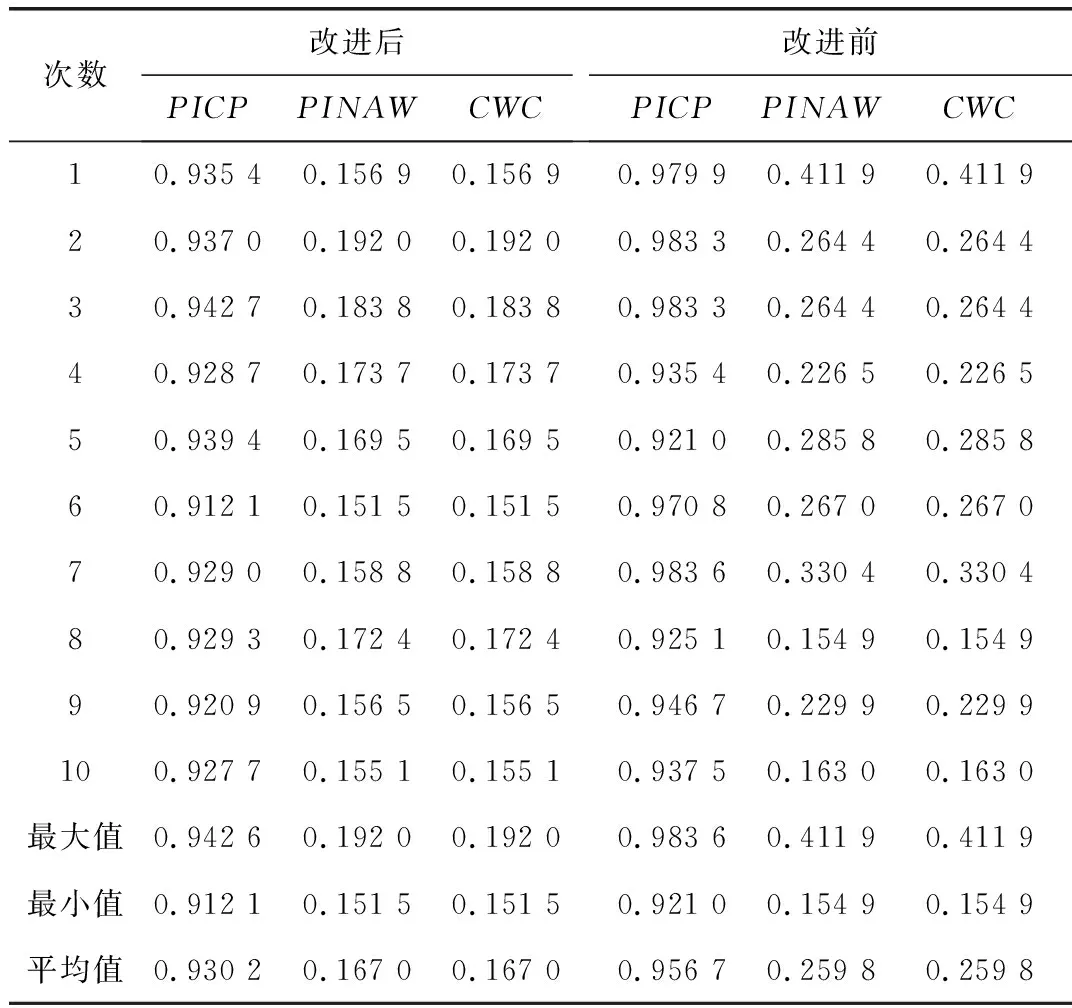
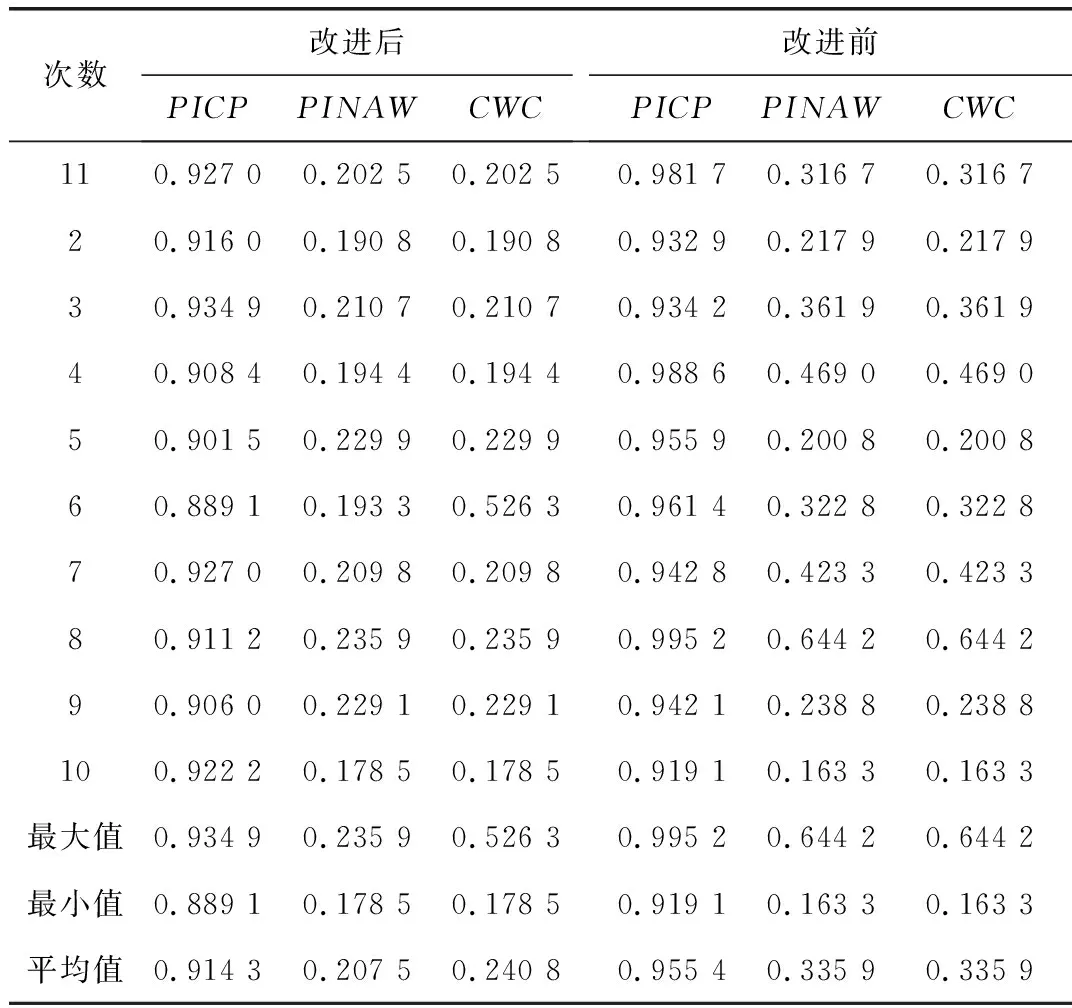
式中el、eu分别为下界和上界的平均拟合误差。因为拟合误差是逐渐优化并最终趋于稳定的,所以期望构建的区间能够跟随输出的预测区间。根据上述假设,在每个训练周期后,若el上升,需要增加构造的区间宽度dl;若eu上升,则需要减少构造的区间宽度du。同时引入参数α用于在每个训练周期后对PICP进行优化,在PICP (13) 式中参数k1用于控制更新速度,参数α的更新策略如式(14)所示: (14) 式中参数k2用于控制α的更新速度。 1.4.2 改进的基于构造区间的自适应优化方法 由于上述方法在实际训练过程中,PICP达到给定PINC的速度较慢,需要比较长的训练周期,且在训练时会出现一定的震荡,因此文中提出改进的基于构造区间的自适应优化方法,采用基于PID思想的闭环自适应调整策略,引入比例和微分控制,加快动态过程,将式(14)调整为: (15) 式中ki1、kp1、kd1分别为积分、比例、微分项控制的系数。积分项用于确保PICP随着训练过程的迭代,最终收敛于PINC附近;比例项根据v(T)的变化趋势来调节α,若v(T) 为了在训练过程中考虑PICP的同时兼顾PINAW,增加参数β用于在每个训练周期后对PINAW进行优化,调整原理与优化PICP类似。因此,在改进的基于构造区间的自适应优化方法中,具体调整过程为: (16) 式中参数k3用于控制区间宽度的更新速度;α和β根据式(17)和式(18)进行调整为: (17) (18) 式中ki2、kp2、kd2分别为积分、比例、微分项控制的系数。由于训练过程中PICP与PINAW的优化存在一定的矛盾,故在训练样本的PICP未达到给定的置信度时,暂不考虑优化PINAW,按照式(13)更新构造的区间宽度。当训练样本的PICP达到给定的置信度时,期望PINAW越小越好,故预设PINAW的训练指标为0,并按照式(16)更新构造的区间宽度。 如图3所示,GRU预测模型的具体训练过程包括以下步骤: 步骤1:对负荷数据样本进行预处理,主要是处理异常数据,并通过划窗将负荷序列划分出特征和标签,归一化后将数据集按8∶1∶1的比例划分为训练集、验证集和测试集; 图3 GRU预测模型训练流程图 步骤2:初始化GRU模型与参数。 步骤2.1:初始化GRU模型的权重和偏差,给定PID参数ki1、kp1、kd1、ki2、kp2、kd2; 步骤2.2:初始设定du、dl、α、β为0,令其在训练过程中进行自适应优化; 步骤3:训练GRU区间预测模型。 步骤3.1:根据式(10),采用当前的du、dl以及标签Y构建训练区间,将训练集样本代入到模型中完成一个周期的训练; 步骤3.2:通过Adam优化算法及式(11)的代价函数计算梯度,并以小批量的形式更新权重和偏差; 步骤3.3:根据式(12)计算平均拟合误差,计算当前预测区间的PICP、PINAW,根据式(17)、式(18)更新α、β。若PICP 步骤4:计算验证集预测区间的CWC指标; 步骤5:若达到最大的训练周期,且存在优质模型则退出训练,否则重复步骤3~步骤4; 步骤6:取出CWC指标最小的模型用于预测。 选取澳大利亚新南威尔士AEMO(2006年~2010年)的历史负荷数据,以及欧洲阿尔巴尼亚(2017年~2019年)的历史负荷数据为样本进行所提区间预测算法性能的验证。 AEMO历史负荷数据采样频率为半个小时一次。应用改进前后的负荷区间预测的方法分别进行短期预测,预测对象为次日全天48点负荷值(从0∶00~23∶30每隔30 min进行一次采样,共计48个采样点)。根据所有的历史负荷数据,以该日之前一周的336(7×48)个点的负荷数据作为输入向量。将模型的验证集以及测试集均划分为182天,剩余的划分到训练集中。设定置信度PINC为93%,改进前后训练集预测区间的PICP和PINAW在训练过程中的变化如图4所示。 图4 改进前后PICP和PINAW在训练过程的变化曲线图 由图4可以看出,改进前的PICP在第35个训练周期达到PINC,但在训练过程中存在一定的震荡,在第70个训练周期后趋于稳定。而PINAW在PICP达到置信水平后,在0.4左右不断震荡,直至在第175个训练周期后开始下降,在训练结束后下降至0.2。改进后PICP在第25个训练周期即迅速接近至PINC,且在接下来的训练过程中趋于稳定。当PICP保持在PINC附近之上,训练的优化方向转向PINAW。PINAW在第25个训练周期后不断下降,训练结束后其值为0.15。综合来看,改进后PICP在训练过程中的变化更加平稳,且能够更快速的达到设定的置信水平,PINAW在PICP稳定后也呈现出下降的趋势,验证了方法的有效性。 改进前后模型对测试集的区间预测结果如图5所示。 图5 改进前后测试集的预测结果图 如图5所示,由于改进后的算法在训练时要对区间平均宽度进行优化,会牺牲一定的区间覆盖率,可能会出现个别实际值超出预测范围的情况。但改进后的预测区间在达到PINC的同时,具有更小的区间宽度,表明其预测区间的效果更好。区间预测置信度PINC分别取0.7、0.8、0.9情况下的区间预测结果如表1所示。可以看出,在区间覆盖率满足置信度要求的前提下,改进后的方法在区间宽度上明显更优,即具有较窄的区间宽度。 表1 改进前后区间预测指标比较 考虑到深度学习算法在多次训练结果上会呈现不一致的情况,分别对改进前后的算法训练10次,取PINC为0.93,记录其区间预测结果指标如表2所示。可以看出,改进后的模型可以保证在PICP达到PINC的同时,PINAW整体会更小,意味着其预测区间质量更高,且改进后的算法训练后得到的10个模型预测结果接近,表明其具有较强的一致性。 表2 改进前后区间预测指标比较(10次训练) 欧洲阿尔巴尼亚(2017年~2019年)的历史负荷数据采样频率为一个小时一次。应用改进前后的负荷区间预测的方法分别进行短期预测,预测对象为次日全天24点负荷值。分别对改进前后的算法训练10次,取PINC为0.9,记录其区间预测结果指标如表3所示,可见文中所提出的基于改进自适应构造区间法的电力负荷区间预测方法在区间覆盖率满足置信度要求的前提下,在区间宽度上明显更优。 表3 改进前后区间预测指标比较(10次训练) 电力负荷具有较强的不确定性,一定置信度下的区间预测方法比点预测方法更加适合描述这种不确定性。考虑到区间预测中有两个量化指标,区间覆盖率PINC和平均区间宽度PINAW,文中对基于GRU模型的自适应构造区间的区间预测方法进行了改进,将PINAW指标引入自适应构造区间的调整策略中,使得区间构造中综合考虑上述两个指标;同时借鉴PID控制的思想,在调整策略中引入了PINC和PINAW的一阶和二阶差分项,对训练过程进行改进。基于澳大利亚新南威尔士AEMO及欧洲阿尔巴尼亚近年的历史负荷数据,对所提出的负荷区间预测方法进行了不同置信度下的验证。结果表明,改进区间预测方法的训练过程更加平稳;在PINC满足置信度的前提下,改进方法得出的PINAW更窄,综合PINC和PINAW的CWC指标更优;同时,改进的区间预测方法对于多次训练具有较好的一致性。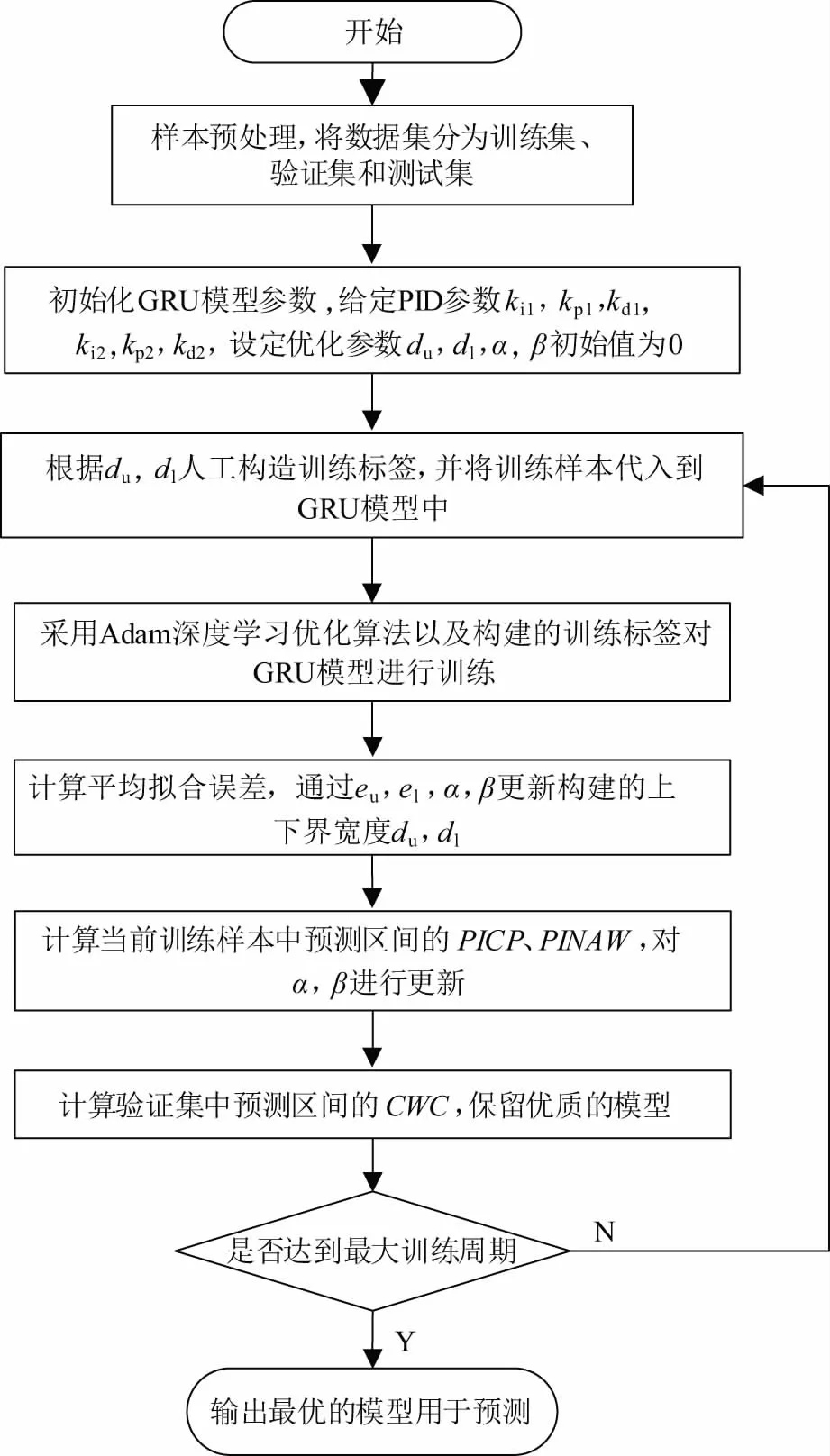
2 算例分析
3 结束语
