基于改进蚁狮优化算法的可再生能源分布式电源优化配置

蔡浩，施凯，唐静，冯霏

(1. 常州工程职业技术学院 智能制造学院，江苏 常州 213164；2. 东南大学 电气工程学院， 南京 210096；3. 江苏大学 电气信息工程学院，江苏 镇江 212013)

0 引 言

随着经济社会的不断发展，对能源的需求程度不断增加，但是生态环境的破坏很大程度上约束了人类对于能源的开采和利用。中国在具有较多能源的同时其本身也是能源消费的大国，经济的快速稳定发展使得能源需求量和消耗量还将继续增加[1-2]。长期来看，有可能面临着能源资源消耗殆尽、供应难度增加、经济发展与生态环境矛盾激化、能源资源利用技术落后等问题。因此，为了在减少功率损耗和废气排放的情况下满足增加的电力需求，在现有的电力网络中引入了基于可再生能源的发电技术。这些可再生能源发电设备通常是以最小规模分布式电源(Distributed Generation,DG)的形式接入配电网用户附近，从而满足电力需求[3]。一方面，DG单元的正确配置具有减少电力损耗、改善电力质量和提高可靠性，同时降低燃料、运行和维护成本等许多优势[4]，但另一方面，DG的位置和容量选择不当会导致功率损耗、成本和电压稳定性等问题增加[5]。

因此，针对配电系统中的分布式电源的优化配置问题，国内外学者进行许多研究[6-9]。文献[9]提出利用细菌落优化算法类对分布式电源进行合理规划。文献[10]利用遗传算法来确定DG单元的合适位置和容量，以有助于降低功率损耗和提高电压。文献[11]提出利用粒子群优化和差分进化来确定合适的DG单元的大小和总线位置，以改善电压分布并减少实际功率损耗。文献[12]使用回溯搜索优化算法对多类型分布式发电机的最佳容量进行了评估，以在增强电压分布的情况下将实际功率损耗最小化。文献[13]利用人工蜂群算法，以获得DG单元的最佳总线位置、尺寸和功率因数，从而最小化配电网的总有功功率损耗。文献[14]提出利用布谷鸟搜索算法优化DG分配，以降低总系统有功功率损耗。文献[15]通过改进的基于教学学习的优化确定了DG单元的合适总线位置和尺寸。文献[16-18]提出利用蚁狮算法来对DG问题进行优化，但问题优化配置的复杂性，上述算法经常陷入局部最优解，可能无法获得DG的最佳位置和容量的理想解。

因此，本文针对可再生能源分布式电源规划配置问题，提出了一种基于改进蚁狮优化算法(Ant Lion Optimization Algorithm,ALOA)的可再生能源分布式电源优化配置方法。该方法首先建立以最小化实际功率损耗和改善配电网电压分布与电压稳定性为目标的多目标函数，然后利用改进蚁狮优化算法[19]，通过模仿自然界中蚁狮的狩猎行为，统筹考虑损耗敏感系数(Loss Sensiticity Factor,LSF)和电压敏感系数(Voltage sensitivity factor,VSF)，推导出不同类型的分布式电源单元的最佳总线位置和容量，最后以IEEE-33总线径向分布系统进行了仿真实验，实验结果表明，与其他算法相比，本文所提算法在降低功率损耗和电压分布方面更优，从而验证了本文所提的算法的适应性和有效性。

1 改进蚁狮优化算法

1.1 算法原理

蚁狮优化算法由Mrrjalili于2015年提出，主要模拟了蚁狮捕猎蚂蚁的狩猎进程进而实现最优值的获取。

在自然界中，蚁狮于捕猎前会在土中利用其巨大的下颚挖出一个漏斗状的陷阱，并藏在陷阱底部等蚂蚁的到来。挖好陷阱后，蚁狮就会苟在底部等待猎物的到来。从图1中可以看出圆锥状陷阱的坡度非常大，蚂蚁很容易不慎落入陷阱的底部。当蚁狮意识到这是猎物时就会发起攻击，但是猎物会疯狂逃跑，此时蚁狮会向斜坡上喷吐沙子以使猎物再次滑落至底部，完成捕食后蚁狮会修整陷阱以等待下一个猎物的到来。

图1 蚁狮算法原理

值得一提的是，蚁狮的行为还与陷阱大小、猎物大小、月亮形状三者的相关性有关。当蚁狮非常饥饿或当晚月亮是满月时，它就会把陷阱挖的更大，因此，在ALO中引入蚂蚁的随机游走实现全局搜索，利用蚁狮的陷阱对蚂蚁进行干扰，通过自适应机制对蚂蚁的位置进行修正，最后基于轮盘赌策略和精英策略来保证种群多样性及算法的整体寻优性能。

1.2 算法模型

ALO算法说明了蚁狮和蚂蚁之间的狩猎机制。为了模拟这种机制，允许蚂蚁在给定的搜索空间内移动，并允许蚁狮使用陷阱捕食它们。为了寻找食物，蚂蚁在自然界随机移动。其随机游走模型表示为：

X(t)=

(1)

其中，rand(t)是一个随机函数，可以用以下等式表示：

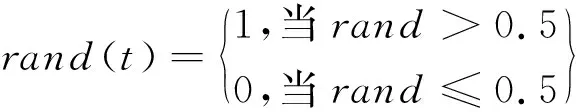
(2)

在优化过程中，使用以下矩阵保存蚂蚁的位置：

(3)

MAnt表示每个解的参数，使用MOA保存优化过程中每个蚂蚁的目标函数的适应度值：

(4)

此外，使用MAl、MOAL保存隐藏在搜索空间中的蚁狮的位置和适应度值：

(5)

(6)

蚂蚁的位置随着公式(1)而改变，将蚂蚁的位置标准化，以便将随机游走保持在搜索空间内，即：

(7)

蚁狮陷阱影响蚂蚁在搜索空间中的随机行走，其影响可表示为：

(8)

(9)

从等式(8)和(9)可以看出，向量c和d使蚂蚁在一个围绕特定蚁狮的超球体中随机行走。蚁狮的捕猎能力是用轮盘赌来模拟的。在ALOA的迭代过程中，借助轮盘赌，根据适应度值选择蚁狮。这为选择出更合适的将蚂蚁诱入陷阱中的蚁狮提供了更高的可能性。

在上述机制的帮助下，蚁狮根据它们的适应度值形成一个陷阱，允许蚂蚁在搜索空间中随机移动。每当蚂蚁掉进陷阱时，蚁狮就会开始从坑中央射出沙子，这使得试图逃跑的被困的蚂蚁滑向蚁狮。将这种行为进行数学建模，蚂蚁超球体半径的随机行走被相应地最小化，表示如下：

(10)

(11)

对于目标函数，如果蚂蚁的目标函数优于所选的蚁狮，那么蚁狮的位置会更新为被追捕蚂蚁的最新位置，这增加了诱捕新蚂蚁的可能性，其公式表示为：

(12)

对于优化过程的每一次迭代，迄今为止获得的最佳蚁狮解决方案被选为精英蚁狮。由于精英蚁狮被认为是最佳解，它应该具有在所有迭代过程中影响蚂蚁运动的能力。因此，假设搜索空间中的每只蚂蚁通过轮盘赌运算和精英策略同时随机地绕着选定的蚁狮行走，如下所示：

(13)

1.3 改进算法

从式(13)可以看出，蚁狮算法前期以围绕轮盘赌选择的蚁狮游走方式为主，后期以围绕精英蚁狮的游走方式为主，为提高算法的搜索能力，本文重点对式(13)进行改进，提出动态比例系数来对式(13)进行调整，从而让不同时期两种游走方式占有的权重不同，即：

(14)

其中T为最大的迭代次数，rand为在0-1之间均匀分布的随机数。

通过对蚁狮算法的改进，使得算法具有一定的随机性，能够有效提高算法前期的探索能力和后期的开发能力，其动态比例系数的使用在一定程度上提升了蚂蚁种群的多样性，从而提升了算法的收敛速度和稳定性。

2 本文所提算法

2.1 最佳分布式电源单元位置确定

本文使用损耗敏感系数来确定分布式电源单元放置的候选总线位置，而电压敏感系数习惯于从候选总线中选择最关键的总线位置来放置DG。电压敏感系数的计算有助于最小化优化过程的搜索区域和时间。

如图2所示，连接在总线i和i+1之间的配电线路的损耗敏感系数使用以下等式来计算：

(15)

电压敏感系数是通过将基础情况下的总线电压除以0.95得到的，如果电压敏感系数值小于1.01的总线则被考虑用于确定DG放置的关键总线位置。

图2 配电网示意图

2.2 目标函数建立

提出了一个以最小化实际功率损耗和改善配电网电压分布与电压稳定性为目标的多目标函数。不同DG单元的最佳总线位置和容量可通过求解以下方程获得：

Ft=min(δ1f1+δ2f2+δ3f3)

(16)

其中，δ1、δ2和δ3为加权因子，分别取为0.5、0.25和0.25，加权因子的绝对和必须等于1。

目标函数中的f1项表示有功功率损耗的最小化，表示为：

(17)

f2表示配电系统中每条总线的电压偏差指数(IVD)，表示为：

(18)

在DG放置过程中，如果系统出现电压越限的情况，这种技术有助于将电压偏差降低到接近于零，从而提高配电系统的电压和电压稳定性。

f3表示配电网电压稳定指数的提高，可表示为：

(19)

其中，VSI的表示为：

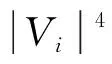
(20)

通过考虑以下等式和不等式约束，使所提出的目标函数最小化。

2.2.1 等式约束

功率守恒约束，对于所有配电网络系统，所有输入功率的算术和必须等于输出功率的总和，即：

(21)

(22)

2.2.2 不等式约束

电压约束，配电系统所有总线的电压曲线必须保持在以下限制范围内：

Vmin≤|Vi|≤Vmax

(23)

2.2.3 DG单元容量限制约束

为了避免配电网络中的反向功率流，DG单元的安装容量不应大于变电站容量，即：

(24)

(25)

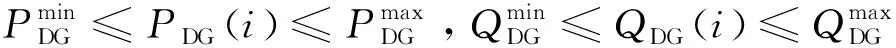
2.3 算法流程

运用本文提出的改进蚁狮优化算法求解2.2节提出的目标函数，具体实现步骤如下：

(1)初始化迭代次数、群体大小和分布式电源容量的大小，设置迭代次数为500，群体为30，分布式电源的容量对应蚁狮优化算法中蚁狮的位置;

(2)计算蚁狮和蚂蚁的LSF、VSF和适应度值;

(3)将最佳蚁狮解决方案指定为精英;

(4)在轮盘赌的帮助下，为每只蚂蚁选择一只蚁狮；进行随机游走，并使用公式(7)将其归一化；使用公式(8)和(9)更新蚂蚁的位置;

(5)确定所有蚂蚁的适应度值;

(6)如果蚂蚁的适应度值大于蚁狮，使用公式(12)更新蚁狮的位置;

(7)如果蚁狮比精英更适合时，更新精英解;

(8)如果达到停止标准，则停止执行，或者转到步骤(4)。

3 仿真实验与分析

本文以IEEE-33总线径向分布系统为例，对分布式电源的位置和容量进行确定和验证，利用python2.7环境进行实验分析，实现平台为独立的Intel Xeon E5-2650处理器，此实验中，蚁狮和蚂蚁的种群规模均为30，每次迭代次数为30，仿真30次，实验结果取平均值。将本文所提出的算法在IEEE 33总线径向分布系统上进行了测试，该测试系统在12.66 kV时的总有功负荷为3 720 kW，无功负荷为2 300 kvar，总线系统图如图3所示。

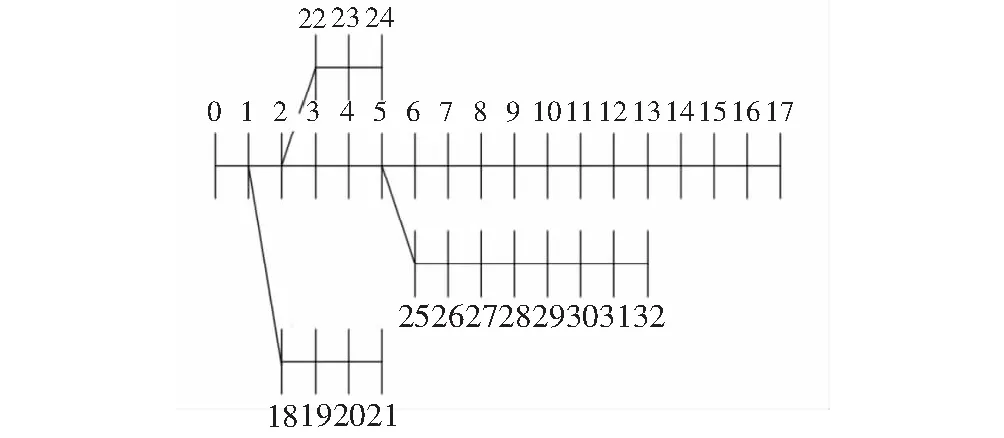
图3 IEEE-33总线系统图

3.1 单个GD放置

表1给出了运用改进ALOA算法确定的不同类型的单个DG单元的最佳总线位置和容量。基于LSF和VSF值，选择6号总线作为单个DG放置的合适位置。容量为2 474 kW的PV型DG将系统的总功率损耗从210.98 kW降至103.36 kW，损耗减少了51%。此外，通过ALOA可以节省35.5126万元的年度成本。DG单元将最小总线电压从0.904 1 提高到0.952 1 。因此，系统的总VSI从26.465 7提高到28.680 3。为进步验证本文所提算法的有效性，将测试结果与文献[10-12,17-18]所提算法进行了比较，结果如表2中所示，从表中可以看出，与其他算法相比，ALOA在功率损耗最小化方面效果更好，在可接受的电压曲线下，功率损耗降低的百分比更高。

表1 本文算法的一个DG单元IEEE 33总线系统测试结果

表2 一个DG单元的IEEE 33总线系统对比结果

WT型DG单元可实现66.26 %的功率损耗减少，总功率损耗为71.18 kW。使用ALOA，每年可节约46.007 8万元。此外，网络的最小总线电压提高到0.951 3，总VSI提高到29.426。从表2可以看出，当与GA和BSOA相关时，ALOA可以最大程度地降低功率损耗。此外，由于其无功功率支持，WT型DG在降低功率损耗、电压分布和VSI增强方面提供了优于PV型的结果。图4和图5给出了安装单个DG单元对配电系统电压分布和VSI的影响。

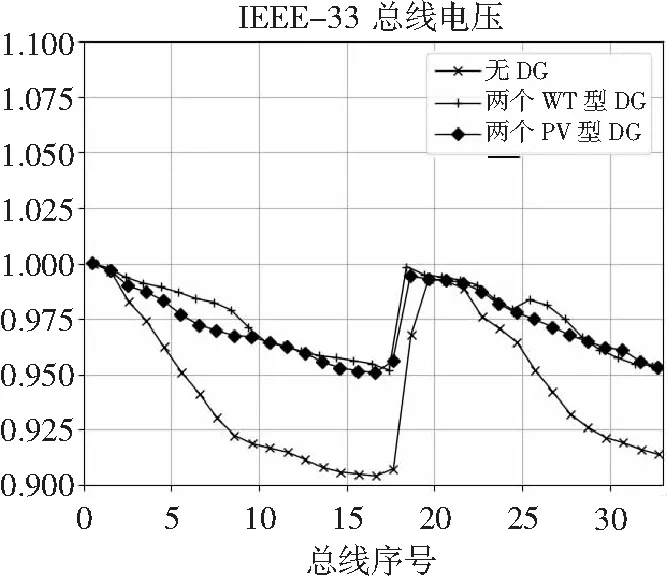
图4 单个DG单元的总线电压曲线

图5 单个DG单元的电压稳定性

3.2 两个GD放置

通过在IEEE 33总线系统上安装两个DG单元，验证了本文所提算法的有效性，13号和30号总线被确定为适合安装容量分别为843.3 kW和1 205.13 kW的PV型DG的位置。如表3所示，在配电网络中添加DG单元可以将总功率损耗降低至80.16 kW，功率损耗降低62 %，最小总线电压从0.904 1 增加至0.971 4 ，且每年的总节能成本为42.742 2万元。为进步验证本文所提算法的有效性，将测试结果与文献[10-12,17-18]所提算法进行了比较， ALOA在降低功率损耗和增强电压曲线方面具有更好的效果。

对于WT型，通过ALOA在最佳总线位置13和30分别获得了918.20 kV·A和1586.22 kV·A的DG容量。总功率损耗为27.13 kW，功率损耗降低了87.15 %，年总节能成本为59.629 8万元。系统的最小总线电压和总分别增加到0.982 4和32.329 1。从表4中可以清楚地看出，ALOA在功率损耗最小化和电压曲线增强方面远胜于BSOA算法。图6和图7分别说明了安装两个DG单元对系统电压曲线和VSI的影响。很明显，WT型DG单元在降低功率损耗、电压分布和增加VSI方面比PV型单元提供了更好的结果。

图 8是给出了本文算法与文献[10-12,17-18]出提的算法在 IEEE-33总线系统网损优化的收敛曲线。通过集中算法的比较可以得知，本文所提的改进蚁狮优化算法，算法更加稳定性，能够得到更高质量优化解，DG 接入配网后系统网损明显小于文献[10-12,17-18]所提的算法，通过对改进的蚁狮算法，使得算法具有一定的随机性，能够有效提高算法前期的探索能力和后期的开发能力，其动态比例系数的使用在一定程度上提升了蚂蚁种群的多样性，从而提升了算法的收敛速度和稳定性。

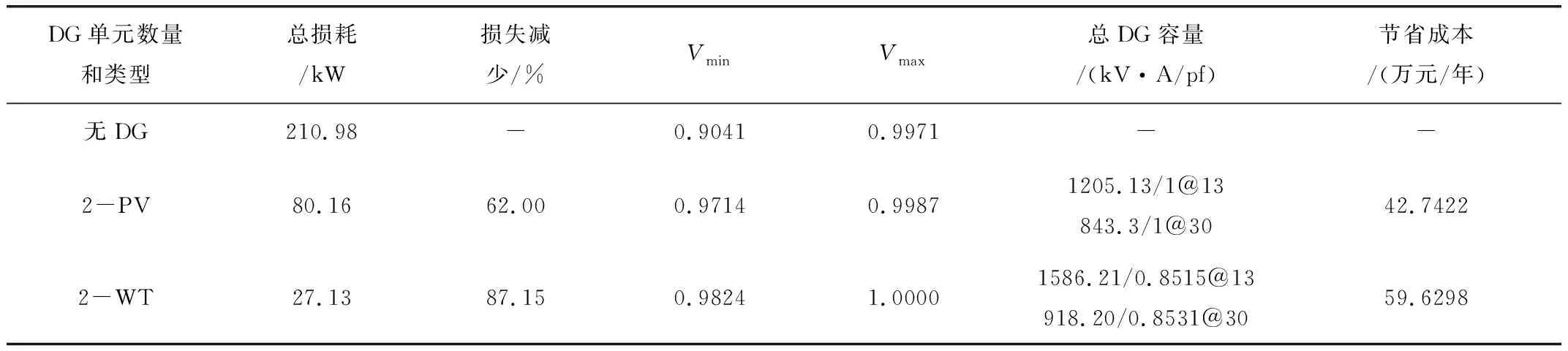
表3 本文算法两个DG单元的IEEE 33总线系统测试结果

图6 两个DG单元的总线电压曲线

图7 两个DG单元的电压稳定性

图8 不同算法收敛图

4 结束语

针对可再生能源分布式电源规划配置热点问题，本文提出了一种基于蚁狮优化算法的可再生能源分布式电源优化配置方法。该方法首先建立以最小化实际功率损耗和改善配电网电压分布与电压稳定性为目标的多目标函数，然后利用蚁狮优化算法，通过模仿自然界中蚁狮的狩猎行为，统筹考虑损耗敏感系数和电压敏感系数，推导出不同类型的分布式电源单元的最佳总线位置和容量，最后以IEEE-33 和IEEE-69节点配电网系统进行了仿真实验，实验结果表明，与其他算法相比,本文所提算法在降低功率损耗和电压分布方面更优，从而验证了本文所提的算法的适应性和有效性。