数据驱动的电力系统动态模型参数误差溯源方法

姜赫，安军，刘征帆，李德鑫

(1. 东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 吉林 132012；2. 国网吉林省电力有限公司电力科学研究院，长春 130021)

0 引 言

电力系统仿真是电力系统稳定分析的重要方法，其结果是指导电力系统运行的主要参考依据，仿真的可信度和准确性直接关系到系统的安全性和经济性[1-2]。在实际运行中，多次出现仿真无法重现电力系统真实的动态行为的问题，仿真的有效性问题越来与越值得被关注[3]。

随着广域测量系统(Wide-Area Measurement System，WAMS)的逐步推广，其在电力系统中得到了广泛的应用[4-5]。借助于 WAMS，人们可以利用扰动时所记录的数据对元件模型进行仿真验证，这是评估模型及其参数有效性的最直接参考依据[6]。同时为基于数据驱动的分析电力系统动态特性创造了有利的条件[7]。

元件模型参数不准确是造成轨迹差异的主要原因，但是大规模电力系统地域广、电力元件众多[8-9]，动态过程较为复杂，很难识出别致差区域，这给我们仿真验证带来了挑战。文献[10]提出了基于WAMS的电力系统分层分块的动态仿真验证策略，利用电网不同电压等级的特点将电网进行分层，在不同层次上进行仿真验证，利用电网元件和区域思想将系统解耦实现仿真验证。但是划分的区域仍然很大，而且只是初步指导，无法准确定位误差元件集，同时元件众多分别解耦计算代价大。文献[11]利用WAMS实测数据与仿真结合，提出混合动态仿真的策略，该方法是在已知子系统模型参数不准确的前提下，才对其进行解耦验证。文献[12]一般基于经验选取受扰较为严重的节点、扰动点附近、或关键联络线进行分析，难以有效反映系统的整体动态行为。因此，亟需寻找有效方法，识别出致差区域。

在大电网系统中可以通过实际的确定性扰动或随机扰动作为激励信号，以识别系统的模型或参数，不同的扰动强度对模型参数的动态激发程度不同，模型参数的验证结果也不同[13-14]。扰动强度不仅与自身的幅度和持续时间有关，还与扰动发生的位置和系统运行状态有关[15]。强度小的扰动只会激发系统平衡点附近的模态，而且系统的响应有可能被噪声湮没[16]，这样对模型参数进行校核势必会造成错解，而且校核的模型参数难以适用于相对大的扰动情况[17]。所以，要在大扰动的场景下，充分激发元件的动态特性，校核出来的模型参数才具有可信性。

同时，仿真结果与实测轨迹特征的差异度是评价模型参数不准确程度的重要指标，也是寻找致差区域的必要条件。轨迹之间差异度大说明模型参数一定存在可信度问题，所以建立受扰轨迹之间的差异度指标，来反映仿真的有效性，是识别致差区域的重要约束条件。

本文针对上述动态仿真验证误差溯源方法的不足及难点，提出了致差区域的概念及其识别方法，通过扰动深度指标描述不同区域的受扰程度，同时验证不同区域内的元件模型的轨迹差异度，通过二者的联合约束确定模型参数致差区域，为电力系统仿真验证提供关键的指导，降低仿真验证的代价，为在线模型参数校核提供参考。

1 致差区域的基本描述

本文所说的致差区域，是指在对参数进行校核前，在多元件参数的大系统中，通过建立指标溯源误差区域，减少验证元件和参数数量，提高动态仿真验证的效率。致差区域是区分“有问题的元件”和“没问题的元件”的标准，正是由于在致差区域内的元件参数有更好的校核效果，所以它们要比区域外的元件参数更有“价值”。因此，参数校核应优先考虑致差区域内的元件参数。

致差区域可以看作模型合理性的评估，作为模型参数校核的前提工作很有意义[18-19]。并不是仿真与实测出现误差就要校核，因为一定的仿真误差也是允许的。如果元件的动态特性没有充分激发出来，其校核的结果有可能脱离物理本质[20]。

下面列出确定元件模型确定致差区域的原则：

若只满足动态激发程度要求，参数准确，即使扰动再大，也无需校核；若只满足差异度的指标要求，而动态特性没被充分激发，则校核后参数泛化能力差。为了轨迹一致性而盲目校核参数，失去校核的意义。

致差区域的确定原则如图1所示。

图1 致差区域的确定原则

2 致差区域识别的关键指标

提出致差区域识别的关键指标的过程，也就是对WAMS获得的大量实测数据进行挖掘的过程。文章以误差溯源为目标，以数据为驱动，提出了扰动深度指标和差异度指标。

2.1 扰动深度指标

对于一次扰动来说，不同节点对整个系统的扰动贡献程度不同，可以从能量的角度来评价不同节点受扰动的影响程度。

对于发电机或节点有功功率数据集，协方差矩阵可以用其中N个数据样本计算，表达式为：

(1)

对于一个维数为n×m的矩阵Z，其能量由Frobenius范数表示：

(2)

因此Csys范数是系统产生的总能量，n是选取节点的数量，m是数据时间序列的个数，同样的对于第i个观测点的协方差矩阵可以表示为：

(3)

通过式(2)的Frobenius范数，可以求取每次扰动中数据集的总能量。因此，第i个测量点的能量含量与整个系统能量含量的比值都可以用作衡量第i个观测点对整个系统扰动贡献程度的指标。这个比率，被称为i观测点的扰动深度，表达式为：

(4)

这里提出一种衡量扰动深度的指标，如果电气量可以被WAMS所记录，用于评估节点受扰程度。

2.2 差异度指标

描述实测与仿真之间的轨迹差异度情况，可以利用有功功率和无功功率的实测轨迹与仿真轨迹进行定性比较。然而，定性的分析验证不足以客观地定义实际子系统的模型的差异度，所以定量指标是必要的。在文献[19]中，MSE(均方根)被用于量化差异度，但它在整个扰动过程中是唯一定值，存在一定的局限性。

在本研究中，提出了差异度指标函数，该函数同时考虑所有输出变量并以百分比表示。

全局差异指标如表达式(5)所示：

(5)

式中Δz=[ΔPΔQ];R是加权矩阵;Sref是用于获得指标的百分比值的参考值。

ξ表示仿真和实测记录数据之间的二次差异值的百分比的累积效应。由于ξ是一个差异指标，当仿真模型能完全替代真实子系统时，它将为0%。ξ不是一个定值，而是一个依赖于时间的函数。该特征使得ξ的其他相关用途成为可能。在本研究中，将Sref定义为额定功率SN。选择矩阵R作为对角矩阵，在对角线元素为100。因此，100%的ξ值对应于SN的平均偏差为10%，对应于平均偏差Z为1%。1%的ξ被认为是可接受的差异。

2.3 致差区域的确定

致差区域既应满足扰动深度指标的约束，又要满足实测仿真轨迹差异度指标的约束(见图2)。

约束条件为：

η0<η<ηmax

(6)

ξ0<ξ<ξmax

(7)

图2 致差区域的确定

设系统有n节点，计算出各个节点的扰动深度以及轨迹差异度，设定阈值ηx、ξx，大于阈值的节点构成集合：

A={η1,η2…ηi}

(8)

B={ξ1,ξ2…ξj}

(9)

式中i、j为节点编号。

对以上两个集合取交集：

C=A∩B

(10)

集合C中包含的节点信息为集合A和集合B的公共节点，即为致差区域。

3 阈值选取的原则

选取的扰动深度与差异度的阈值的不同，致差区域范围也随之变化。若选取的阈值较小，将会使致差区域相应缩窄，涵盖的元件参数不够可信，从而降低溯源结果的准确性。反之，选取的阀值过大，则使得致差区域过于宽泛，无法实现溯源(见图3)。

图3 不同阈值下的致差区域

需要指出，由于一些算法等的原因，即使模型参数非常准确，动态仿真也可能出现与实测的不一致。此时，不应对其模型参数进行校核。如果误差指标过小，就会把此类问题归于致差区域，这是不合理的。对于用ξ描述的仿真和实测记录数据之间的二次差异值的百分比的累积效应，1%的误差值，变化量相当于额定功率的1%，可以认为是可接受的误差范围，即选取的误差指标不能太小。

扰动深度是通过计算扰动过程中各个节点能量占总能量的比值来确定的[21]。大多情况下，扰动发生后，扰动深度较高集中于一个区域内。通过多次试验对比分析，扰动深度在0.2以下，所受扰动的影响较小，动态特性激发不明显。

阈值的选取不是绝对的，根据经验，针对各种不同的条件适当选取即可。

4 算例分析

4.1 算例条件

以IEEE 10机39节点系统(见图4)为例，在节点11设置三相短路，1 s开始，1.1 s结束。分别摄动32与37节点发电机参数1.5倍(参数包括xd、xq、xq′、Td0′)，使得节点32与节点37发电机模型参数产生误差。确定出致差区域，并对其中的元件模型进行参数校核，并验证致差区域的合理性。

图4 IEEE 39节点系统结构图

摄动参数后32、37节点的电压及32、37节点上的发电机模型的有功功率、无功功率轨迹特征分别如图5～图8所示。

图5 32节点发电机模型参数摄动前后32节点电压幅值对比图

图6 37节点发电机模型参数摄动前后37节点电压幅值对比图

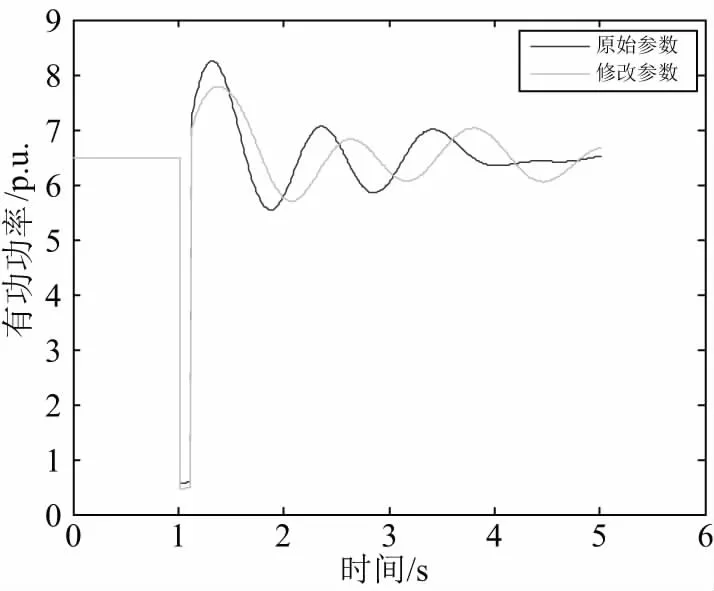
图7 32 节点发电机模型参数摄动前后32节点发电机模型有功功率对比图

图8 37节点发电机模型参数摄动前后37节点发电机模型有功功率对比图

参数摄动后，32、37节点电压以及32、37节点上的发电机模型的有功功率产生了很大的差异。

4.2 确定致差区域

计算各个节点的扰动深度指标以及差异度指标。39个节点的扰动深度指标的分布如图9所示,各个节点差异度指标如图10所示。

图9 各节点扰动深度指标的分布情况

图10 各节点的差异度指标分布情况

在此选取扰动深度指标阈值为ξ= 0.2、差异度指标阈值为η= 1%，得到满足阈值的节点号，如表1所示。

根据扰动深度指标和差异度指标确定出32节点在致差区域内，37节点在致差区域外(见表1)。

4.3 致差区域合理性的分析

分别对这两台发电机进行参数校核，对比校核后模型参数的泛化能力。

(1)校核32节点发电机的参数后，在25节点设置三相短路故障，验证模型参数是否能重现该扰动行为。32节点发电机模型原参数、摄动后参数、校核后参数如表2所示。

对32节点发电机参数进行校核，用其他扰动进行验证，可以看到，校核后的参数所进行的仿真基本上反映该扰动的动态特性。模型的泛化能力较好。

校核模型参数后，在25节点设置扰动，32节点仿真轨迹情况如图11～图13所示。

图11 32节点发电机模型在原参数下和校核后参数下的32节点电压幅值对比图

图12 32节点发电机模型在原参数下和校核后参数下的有功功率对比图

图13 32节点发电机模型在原参数下和校核后参数下的无功功率对比图

(2)校核37节点发电机的参数后，在25节点设置三相短路故障，验证模型参数是否能重现这次扰动。37节点发电机模型原参数、摄动后参数、校核后参数如表3所示。

校核模型参数后，在25发生设置扰动，37节点仿真轨迹情况如图14～图16所示。

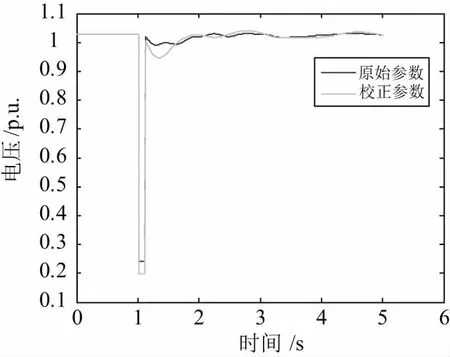
图14 37节点发电机模型在原参数下和校核后参数下的37节点电压幅值对比图

图15 37节点发电机模型在原参数下和校核后参数下的有功功率对比图

图16 37节点发电机模型在原参数下和校核后参数下的无功功率对比图

使用修改后的模型参数验证该次扰动过程，有功功率偏差很大，不能重现该次动态行为，模型参数泛化能力不强。

综上，在致差区域内的模型参数校核效果更好，泛化能力更强；在致差区域外的模型参数校核后，泛化能力不强。通过对致差区域内模型参数校核后，仿真精度充分得到改善，说明致差区域的划分是合理的。

5 结束语

针对大规模电力系统动态仿真验证元件及其参数众多，定位元件参数致差区域困难的问题，文中提出数据驱动的误差溯源方法。定义了扰动深度指标和差异度指标，分别用来量化描述扰动后元件受影响的严重程度及实测与仿真轨迹差异度；并通过约束条件定位出模型参数致差区域。能有效减小电力系统仿真验证代价。同时，验证了致差区域内的模型参数校核后泛化能力强。该方法为电力系统动态仿真验证误差溯源提供了新思路，具有一定的指导意义。