讲题比赛特等奖获奖论文之四：八方联系 浑然一体——2022年高考数学全国甲卷理科第22题的解法研究

云南师范大学实验中学 冷天存

昆明市第八中学 阮媛媛 张婷

1 题目呈现

(1)若f(x)≥0，求a的取值范围；

(2)证明：若f(x)有两个零点x1,x2，则x1x2<1.

2 第(1)问解法探究

2.1 思路分析

思维导图如图1所示：

图1

2.2 具体解法

通法1:分离参数.

解：f(x)的定义域为(0,+∞).

令g′(x)=0，得x=1.当x∈(0,1)，g′(x)<0，g(x)单调递减；当x∈(1,+∞)，g′(x)>0，g(x)递增.故g(x)min=g(1)=e+1，从而a≤e+1.

所以a的取值范围为(-∞,e+1].

点评:分离参数法是求参数取值范围的常用方法.

通法2:利用函数最值.

解：f(x)的定义域为(0,+∞).

令f′(x)=0，得x=1.当x∈(0,1)，f′(x)<0，f(x)递减；当x∈(1,+∞)，f′(x)>0，f(x)单调递增.故f(x)min=f(1)=e+1-a.

若f(x)≥0，则e+1-a≥0，即a≤e+1.

所以a的取值范围为(-∞,e+1].

点评：求函数的最值是求参数取值范围的常用方法.

通法3：数形结合.

图2

当x∈(0,1)时，g′(x)<0，g(x)单调递减；当x∈(1,+∞)时，g′(x)>0，g(x)单调递增.所以g(x)min=g(1)=e.

当x∈(0,1)，h′(x)>0，h(x)单调递增；当x∈(1,+∞)，h′(x)<0，h(x)单调递减.所以h(x)max=h(1)=-1+a.

由图2可知，要使f(x)≥0，只需满足g(1)≥h(1)，即e≥-1+a,故a≤e+1.

故a的取值范围为(-∞,e+1].

点评：数形结合是求参数取值范围的常用方法，本题中通法3没有通法1和通法2简便，但是在某些题中会很适用.

技巧1：同构化简函数再求参数范围.

令μ=u(x)=x-lnx,则g(μ)=eμ-μ-a.

当x∈(0,1)，u′(x)<0，u(x)单调递减；当x∈(1,+∞)，u′(x)>0，u(x)递增.所以u(x)min=1.

又g′(μ)=eμ-1>0，g(μ)单调递增，所以g(μ)min=g(1)=e+1-a,从而f(x)min=e+1-a.

若f(x)≥0，则e+1-a≥0，即a≤e+1.

所以a的取值范围为(-∞,e+1].

点评:这个方法在第(1)问中相对于通法1、通法2和通法3，在解法上没有很大优势，但如果第(1)问观察函数f(x)的结构，通过构造函数μ=u(x)=x-lnx，可以为第(2)问作铺垫.

技巧2：利用“指对”不等式放缩后求参数范围.

所以a的取值范围为(-∞,e+1].

点评:此法虽不是求参数范围的通法，但是是根据“指对幂”之间经典的放缩变形而来，十分简洁，笔者以为是解决该题最简便的方法.

技巧3:必要性探路求参数范围.

解：必要性.要使f(x)≥0恒成立，则至少需要f(1)≥0，即e+1-a≥0，解得a≤e+1.

综上，a的取值范围为(-∞,e+1].

点评:此法的绝妙之处在于先给出答案.对于恒成立问题，找到端点，先分析必要性得出结论，再想办法证明充分性，但是端点是否能找对需要学生具备“题感”.

3 第(2)问解法探究

3.1 思路分析

思维导图如图3所示：

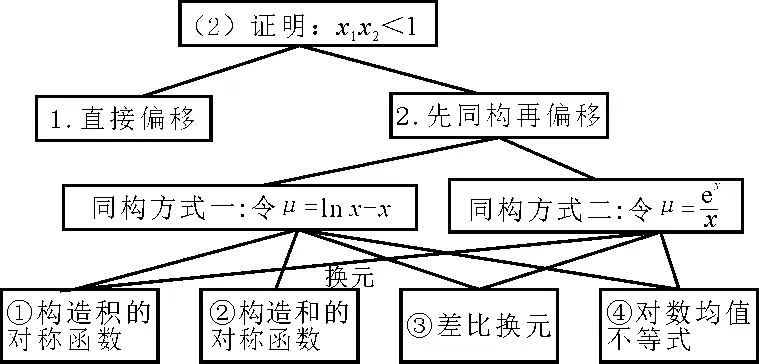
图3

3.2 具体解法

解法1:构造积的对称函数——利用导函数判正负.

由(1)知，当x∈(0,1)，f′(x)<0，f(x)单调递减；当x∈(1,+∞)，f′(x)>0，f(x)单调递增.则f(x)min=f(1)=e+1-a.

若f(x)有两个零点，则e+1-a<0，即a>e+1.

所以r(x)>r(1)=0，即g′(x)>0，g(x)在(1,+∞)上单调递增，g(x)>g(1)=0.

解法2:构造积的对称函数——利用双函数判正负.

由(1)知，当x∈(0,1)时，f′(x)<0，f(x)单调递减；当x∈(1,+∞)，f′(x)>0，f(x)单调递增.则f(x)min=f(1)=e+1-a.

解法3:先同构再构造积的对称函数.

f(x)的定义域为(0,+∞).

当x∈(0,1)，u′(x)<0，u(x)单调递减；当x∈(1,+∞)，u′(x)>0，u(x)递增，所以u(x)min=1.

又函数y=eμ+μ-a单调递增，所以由f(x1)=f(x2)可得u(x1)=u(x2).

点评:在这个方法中要学会观察函数f(x)的结构，通过同构函数u(x)=x-lnx，进而由f(x1)=f(x2)可得u(x1)=u(x2)，此时再构造积的对称函数.在这个方法中由于函数u(x)的结构比f(x)简单，所以证明过程也变得简洁.

解法4:先同构再构造和的对称函数.

由解法3可得x1-lnx1=x2-lnx2.

由u(x)的单调性可设0

令t=lnx，则et=x.问题可以转化为“当et1-t1=et2-t2，证明t1+t2<0”.

令g(t)=et-t，则g′(t)=et-1，所以g(t)在(0,+∞)上单调递增，在在(-∞,0)上单调递减，则g(t)min=g(0)=0.

不妨设t1<0g(-t2).

令h(t)=g(t)-g(-t),t∈(0,+∞)，则h′(t)=g′(t)-g′(-t)=et-1+(e-t-1)=et+e-t-2>0，所以h(t)在(0,+∞)上单调递增，故h(t)>h(0)=0.

问题得证.

点评:解法4是证明此类问题的常用方法，将构造积的对称函数转化为构造和的对称函数，有时会使化简过程变得简洁.

解法5:同构简化问题再比值换元.

由解法3可得x1-lnx1=x2-lnx2,移项得

①

不妨设0

解法6：同构简化问题再差值换元.

由解法3可得x1-lnx1=x2-lnx2,移项得

不妨设0

解法7:先同构再利用对数均值不等式.

由解法3可得x1-lnx1=x2-lnx2，即

解法8:另一种同构简化问题再构造对称函数.

f(x)的定义域为(0,+∞).

当x∈(0,1)，u′(x)<0，u(x)单调递减；当x∈(1,+∞)，u′(x)>0，u(x)递增.所以umin=e.

所以g(x)在(1,+∞)上单调递增，g(x)>g(1)=0.

点评:解法8属于另外一种同构，这种同构方式也适用于解法5、解法6、解法7的解题思想.读者可以自行尝试，本道题还可以再有三种解法.

4 总结

对于本题，极值点偏移是基本方法，但是构造函数各有不同.一方面可以直接偏移构造积的对称函数，此时可以直接研究该对称函数在定义域上的正负，亦或者分解为双函数比较大小.另一方面可以先通过指对幂三者之间的关系进行同构再偏移，此时构造函数便多种多样，可以构造积的对称函数、和的对称函数，还可以通过差比换元化简运算后构造函数.最简便的要数一眼看穿结构，利用对数均值不等式直接证明.整体来看，在极值点偏移问题中，如能进行同构化解函数，将对证明问题有极大的帮助.

从本题以小观大，我们可以看出极值点偏移是双变量问题的一种，涉及到换元思想、构造思想、对称思想等.解决极值点偏移问题最常用的思想是对称思想，方法上的体现是构造积或者和的对称函数；也会用到换元思想，方法上的体现是差比换元；也会涉及同构思想，方法上的体现是构造相同结构，将问题简化；同时，极值点偏移常常也和对数均值不等式联系在一起，使解法锦上添花.