讲题比赛特等奖获奖论文之三：2022年上海高考数学第12题解析

上海市西外外国语学校 朱大红

1 压轴题呈现

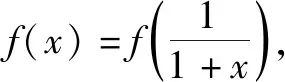
2 试题说明

3 解法分析及详解

本题为压轴题，考查抽象函数的定义域、值域，利用转化化归、数形结合等方法解决参数问题.依据思维导图，有如下四种解法.

思路一：分拆定义域.

第一步：分拆定义域.[0,+∞)=[0,a]∪[a,+∞)，得到f(x)在[a,+∞)上的取值范围为其值域的子集，即{y|y=f(x),x∈[a,+∞)}⊆Af.

思路一的思维导图如图1所示.

图1

解法1：记f(x)在[a,b]上的取值范围为f[a,b]，下同.

由[0,+∞)=[0,a]∪[a,+∞)，结合已知条件{y|y=f(x),x∈[0,a]}=Af，得

Af=f[0,+∞)=f[0,a].

则{y|y=f(x),x∈[a,+∞)}⊆Af，即

f[a,+∞)⊆Af.

思路二：数形结合.

思路二的思维导图如图2所示.

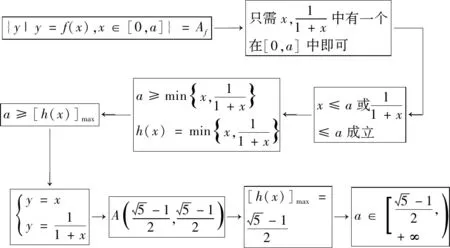
图2

图3

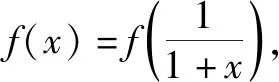
思路三：类比法.

思路三的思维导图如图4所示.

图4

解法3：因为f(x)满足

思路四：考虑临界点.

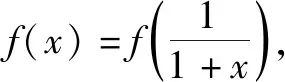
思路四的思维导图如图5所示.

图5

4 变式与拓展

问题对于该题，你是否能举一个f(x)的例子？

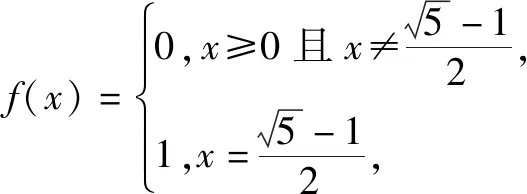
思考：本题是否还有其他f(x)的例子？如果有，请尝试给出表达式，并作进一步探究.