一种基于模拟退火思想的锥模型信赖域方法
2022-11-22杨月婷王宏博周国玲曹名圆
杨月婷,王宏博,周国玲,李 蓉,曹名圆
(北华大学数学与统计学院,吉林 吉林 132013)
0 引 言
考虑无约束优化问题
(1)
其中f(x):n→是连续可微函数.信赖域方法是求解问题(1)的有效方法之一[1-3],其基本思想为在信赖域内求解近似子问题的极小点,以便寻找使得函数值下降的新迭代点.该过程一般借助二次函数构造信赖域子问题,但是,在目标函数具有高度非二次性或曲率变化剧烈时,其逼近效果较差[4].因此,许多学者致力于研究基于锥模型的信赖域方法[5-7].
ZHAO等[5]充分利用前一次迭代点和当前迭代点的信息,采用新的自适应策略调整信赖域半径,提出基于简化锥模型的非单调自适应信赖域方法.该算法具有局部的超线性收敛速度,且更适用于大规模问题.LI等[6]提出新的非单调信赖域Barzilai-Borwein(BB)方法.该方法利用标量矩阵近似信赖域子问题中目标函数的Hessian阵,其中标量矩阵的系数为BB方法步长的倒数,基于改进的Metropolis准则更新迭代点.该方法可以显著减少迭代次数并提高算法的收敛速度.
受文献[5-6]启发,本文利用牛顿插值多项式构造简化锥模型,基于模拟退火思想改进的Metropolis准则更新迭代点,提出基于模拟退火的锥模型信赖域方法.证明了新算法的全局收敛性,并给出数值结果验证算法的有效性.
1 算法的提出
考虑锥模型信赖域子问题
(2)
其中fk=f(xk),gk=g(xk),Bk∈n×n是函数f(x)在当前迭代点xk处的Hessian阵或Hessian阵的近似,s是试探步,Δk>0是信赖域半径,bk∈n是水平向量.水平向量的取法很多,本文采用较经典的取法[8],即
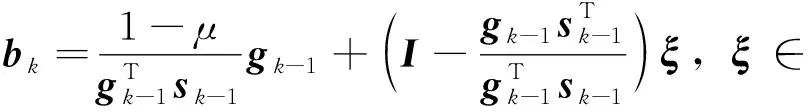
(3)

我们用γkI(γk>0)近似Bk,得到式(2)的简化锥模型信赖域子问题
(4)
为了确定参数γk,利用插值条件
ψ(k)(xk-1)=fk-1, ∇ψ(k)(xk-1)=gk-1.
(5)
令sk-1=xk-xk-1,由式(5)得

(6)
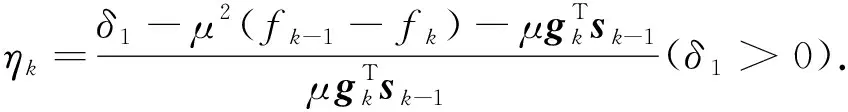
(7)
以确保γkI的正定性.
经典信赖域方法通过实际下降量与预测下降量的比值
(8)
来决定是否接受试探步以及如何调整信赖域半径.为了接受更多的试探步,提高算法的效率,本文引入带有温度的Metropolis准则[6]
(9)
来决定是否接受试探步,其中Tk是第k次迭代时的温度,0<τ<1是足够小的实数.通过冷却技术,当k→∞时,温度Tk下降到0.将Metropolis准则嵌入到信赖域准则,使用pk与rk相结合,判断算法是否进行迭代.与经典信赖域算法不同的是,当rk≤τ时,使用Metropolis准则以一定的概率接受更多的迭代,从而减少计算量,提高算法的收敛速度.
基于以上分析,我们给出基于模拟退火的锥模型信赖域算法(Conic model trust region method based on idea of simulated annealing,SACTR).
SACTR算法
步1 给定x0∈n,ε>0,Δ0>0,T0>0,v>1,0<β<1,0

步3 求解信赖域子问题(4),得到试探步sk.
步4 通过式(8)和式(9)分别计算rk和pk.令
(10)

步5 更新信赖域半径
(11)
步6 由式(6)或式(7)计算γk+1.如果γk+1≤κ或γk+1≥1/κ,则γk+1=θ.


(12)
2 SACTR算法的全局收敛性
为证明SACTR算法的全局收敛性,给出如下假设条件:

(H2)函数f:n→在水平集L(x)上连续可微,且∇f(x)满足Lipschitz连续条件,则存在正常数MH,使得

(H3)假设存在两个正常数Δmax和Mb,使得

.
(13)


(14)


(15)


(16)
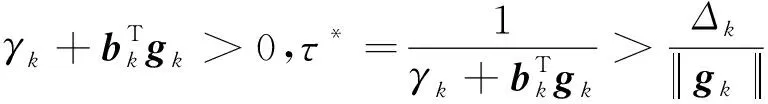

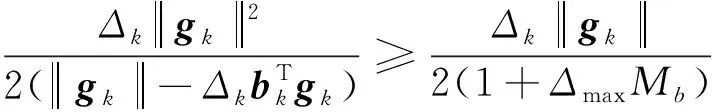
(17)

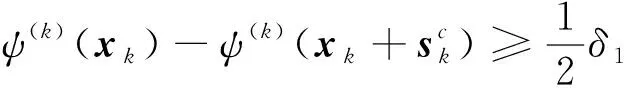
(18)
且sk是子问题(4)的解,所以有
因此

证毕.
引理2假设(H3)成立,序列{xk}由SACTR算法生成,则存在一个充分大的N>0,当∀k>N时,有

证明:由SACTR算法步4可知,如果rk≥τ>0,则pk=1>lk.由引理1得
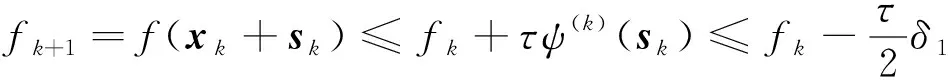
(19)



(20)
综上,引理得证.证毕.
引理3假设(H2)成立,序列{xk}由SACTR算法生成.如果xk不是问题的解,即g(xk)≠0,则pk≤lk的迭代必为有限次.

(21)
由Δk+1=η1Δk,得
和
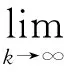
结合SACTR算法步6,可得序列{γk}是一致有界的,即
(22)

(23)
根据二阶泰勒展开以及式(22)和式(23),可得
|[f(xk)-f(xk+sk)]-[ψ(k)(xk)-ψ(k)(xk+sk)]|=

其中ζk∈(0,1).因为k充分大,从式(22)和引理1,有

(24)
取K=max{K1,K2},当k>K时,式(21)和式(24)同时成立,矛盾.证毕.
定理1假设(H1)成立,序列{xk}由SACTR算法生成,则

(25)
证明:若SACTR算法在有限步终止,那么结论显然成立.
考虑无限多次成功的迭代.根据假设(H1)可知f(xk)有界,即存在a∈,使得对∀k,都有f(xk)≥a.由引理2得

(26)
对式(26)的k产生增量

(27)
注意到,对∀K>0,有fN+K+1>a.对式(27)取K→∞的极限,得
即式(25)成立.证毕.
3 数值实验

因为Metropolis准则以一定的概率接受更多的试探步,我们通过多次运行算法得到的平均迭代次数和平均CPU运行时间来表明算法效率.为了更清晰的展示算法的数值效果,采用Dolan等[9]性能图对算法的迭代次数和CPU运行时间进行评估.我们以CPU运行时间为例,在性能图中横坐标τ表示最佳比值因子,纵坐标ψ=ρν(τ)表示某算法在运行时间与所有算法中最少运行时间的比值不超过τ时所求解问题个数占问题总数的比率,它反映了所测算法在运行时间方面的性能.因此,本文对SACTR算法、SAQTR算法及SATRBB算法,以τ为横坐标、ρν(τ)为纵坐标作图,图中曲线越高表明算法的数值性能越好.三个算法的性能评估结果如图1所示.

图1算法性能对比Fig.1Comparison of algorithm performance
从图1 a中可以看出,在迭代次数方面,SACTR算法的性能曲线整体趋势优于SATRBB、SAQTR的曲线趋势,表明SACTR算法在求解无约束优化问题时能够使用更少的迭代次数,求解效率更高;图1 b表明SACTR算法在CPU时间上也优于SATRBB和SAQTR算法.
4 结 论
本文提出了求解无约束优化问题的基于模拟退火的锥模型信赖域方法,在适当假设条件下,证明了算法的全局收敛性.数值结果表明,SACTR算法无论是在迭代次数,还是在CPU时间上都是有竞争力的,特别是对于非二次型的函数.
