具有分数阶非线性金融风险系统模型的动力学行为控制
2022-11-22刘国欣
李 博,刘国欣,张 霞
(1.河北工业大学 经济管理学院,天津 300000;2.中国银行股份有限公司 河北省分行,河北 石家庄 050000;3.石家庄铁道大学 数理学院,河北 石家庄 050043;4.石家庄铁道大学 交通运输学院,河北 石家庄 050043)
在金融研究领域,金融风险系统自身参数的变化导致金融风险系统混沌.非线性复杂金融风险系统中部分变量具有记忆性,采用分数阶微分理论可以对其演化特征进行分析[1].分岔和混沌是存在于非线性金融风险系统中的一种复杂现象,在这方面已经取得了一些前期成果.辛宝贵等[2]定性地分析一类分数阶混沌金融系统的均衡解的稳定性及Hopf分岔发生的条件,通过分岔图、相图和时间序列图对该系统的复杂性演化行为进行仿真研究.徐争辉等[3]研究了一个对称分数阶经济系统混沌的特性.毛北行等[4]研究了一类分数阶金融系统的混沌同步问题,给出了两种系统实现同步的控制方案,并用仿真算例表明了方法的有效性.张文娟等[5]提出了一类分数阶的金融风险模型,研究了风险模型对参数初始值的敏感依赖性,并构造了风险模型的受控系统,数值模拟结果表明该控制方法可以有效地控制混沌.
运用非线性动力学中的混沌和分岔理论,对分数阶金融风险系统进行有效的预测和控制,一直是经济学家研究的热点.越来越多的学者关注金融系统的稳定运行、金融风险的稳定控制.可通过对系统混沌、分岔等问题的研究,采取混沌控制策略,有效地实现对金融系统混沌现象的控制.目前,常用的混沌控制策略可分为反馈控制[6-8]和无反馈控制[9].
因此,利用非线性动力学中的混沌和控制理论研究该分数阶金融风险系统的混沌动力学行为,找出合理的混沌控制方法是非常有必要的,是防范金融风险、防止金融危机发生的有效手段之一.
1 分数阶金融风险模型及其混沌动力学行为
近年来,许多研究者认为实际系统通常大都是分数阶的.与整数阶微积分相比,分数阶微积分具有记忆特性,可以很好地描述金融风险非线性系统历史发展的依赖过程,采用分数阶方法能更好地描述金融风险的本质[10-13].为了研究该金融风险系统的分数阶形式,在论文中采用Caputo微分形式[14]
(1)
其中:n-1≤α≤n, Γ(·)是Gamma函数.
将该分数阶微分形式引入金融风险系统[15]中,将其扩展成为如下分数阶金融风险系统
(2)
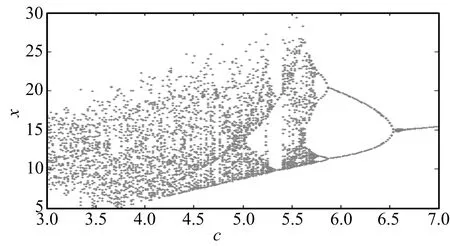
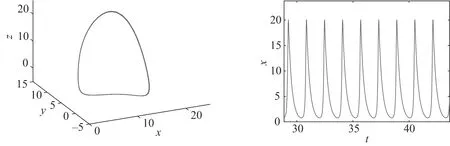
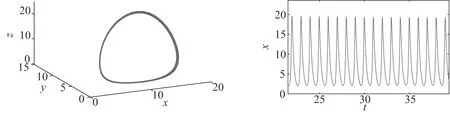
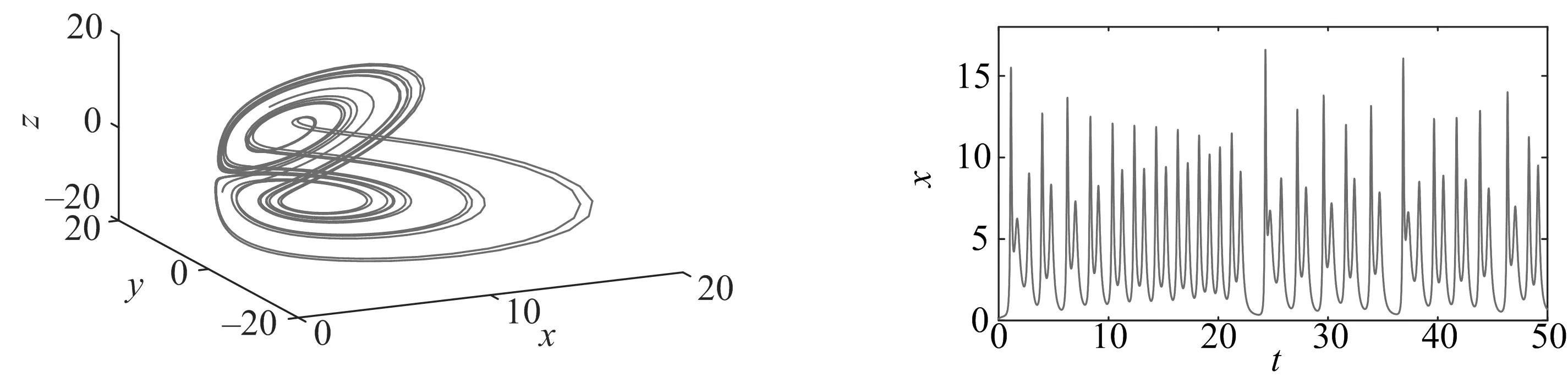
其中:x表示金融资产的价格,如利率、汇率、股票价格指数、黄金价格等;y表示投资需求;z表示价格指数;0 命题[16]对于给定的分数阶非线性系统 (3) 其中:0 假定qi=υi/ui,(υi,ui)=1,ui,υi∈+.令γ=1/m(m是ui的最小公倍数),有 det(diag([λmq1,λmq2,…,λmqn])-J)=0, (4) 其中:J=∂f/∂x.如果上面特征方程的所有根λ满足|arg(λ)|>πγ/2,则分数阶非线性系统是渐进稳定的. (5) 分数阶金融风险系统的Jacobi矩阵为 (6) 由于分数阶金融风险系统是非线性系统,根据式(4),得 (7) 通过求解方程组(5),可从以下3种情况进行分析. 当c=1时,系统(2)的平衡点是(0,0,0),将其代入式(7),得 (8) 当0 对于系统中的4个非零平衡点,设其为(a0,b0,c0),将其代入式(7),得 (9) 如果由式(8)和(9)所得出的特征方程的所有特征根满足|arg(λ)|>πγ/2,则分数阶金融系统(2)是渐进稳定的.以下对系统(2)在具体参数条件下进行稳定性分析. 若系统中各参数取值为a=4,b=8,q1=q2=q3=0.9时,此时m=10,γ=1/m=1/10=0.1,下面分两种情况进行讨论. 当0 (λ9+5)(λ9+9)(λ9-c+1)=0. (10) 当1 λ27+11λ18+540=0. (11) 对式(11)进行求解,得到特征方程的各个特征根及其所对应的幅角模,如表1所示. 表1 特征根及其所对应的幅角模 由表1可知,系统特征方程的特征根所对应的最小幅角模值为|arg(λ26,27)|=0.149 2<γπ/2=0.157 1,不满足命题所提出的判别条件,因此,可以判断系统在此参数条件下不是渐进稳定的. 若系统中各参数取值为a=4,b=7,c=3,q1=0.8,q2=q3=0.9时,此时m=10,γ=1/m=1/10=0.1. 当平衡点为(0,0,0)时,系统的特征方程为 (λ9+5)(λ9+9)(λ9-2)=0. (12) 当平衡点为非零平衡点时,将系统各参数代入式(9),得到系统的特征方程为 λ26+5λ18+6λ17+320=0, (13) 通过计算,方程(13)无解,因此,系统(2)在此参数条件下的稳定性无法判断. 综上可知,风险程度a、单位投资成本b、调控强度参数c取值不同时会影响分数阶金融风险系统平衡解个数及其稳定性.实际上,不合理的参数取值会导致产生分数阶金融风险系统的分岔与混沌等复杂的动力学行为,如图1所示.从图1可知,随着c值的减小,逐渐从平稳的周期运动状态进入混沌状态.当c=4时,系统处于混沌运动状态.当c=5.75时,系统处于概周期的运动状态,说明随着c值的增大,调控起了一定的作用,但是系统的周期性依然不是很好,还需要加大控制强度.随着c值的增大,系统周期性继续提高,当c=6.3时,系统处于倍周期的运动状态,但是系统的周期性依然不理想.当c=7时,系统处于周期1运动状态,是金融系统运行的理想状态.因而如何控制金融风险系统处于周期运动必不可少. 图1 系统的总风险值x随c变化的分岔图 采用逆优化控制法[17]和增加反馈增益控制法[18]来对分数阶金融系统进行混沌控制,不仅可控制周期运动状态,还可控制平衡解状态.通过数值仿真比较控制前后金融系统的动力学行为,讨论了控制方法的鲁棒性,说明了控制方法的正确性及有效性. 考虑分数阶金融系统模型(2).将利用逆优化控制算法控制分数阶混沌系统的状态变量到其平衡点,在方程(2)的第二个方程中加入控制函数u,则受控系统变为 (14) 其中:u是线性反馈控制器.控制率基于逆优化控制算法,该算法已成功被应用于整数阶Chen系统的混沌控制[19].该节将利用该算法的思想控制含分数阶金融系统的混沌动力学行为.该控制率可描述为 (15) 其中:u表示对系统内部传染效应下总风险值的控制强度,其大小与第1,2阶段的风险程度有关. 图2 控制前、后系统的相图与时间历程图 由图2可以看出,增加控制器后,分数阶金融系统由原来的混沌运动状态变为稳定的周期运动状态,控制方法简单有效. 在分数阶金融风险模型(2)的基础上,构造受控系统[20] (16) 其中:(m1,m2,m3)为系统的正反馈增益系数,表示系统的控制强度;(x′,y′,z′)为模型(2)的平衡点,也是模型(5)的平衡点. 图3 控制前、后系统的相图与时间历程图 通过分析图3可知,分数阶金融风险模型(2)的不可控状态,可利用增加反馈控制器达到稳定运行状态.此外,随着反馈增益系数m1,m2和m3的增加,系统控制强度增加,系统周期性有所提高,系统由概周期运动变为周期运动,最后变为衰减运动,混沌运动完全消失. 对原系统参数a,b的值同时增加或减少,即对系统加入一定量的扰动后,考察控制方法的鲁棒性能. (i)逆优化控制.对系统中参数a,b的值分别减小25%,分析系统的运动状态,如图4所示. 图4 逆优化控制系统的相图和时域图 对系统中参数a,b的值分别增加25%,分析系统的运动状态,如图5所示. 图5 逆优化控制系统的相图和时域图 由图4,5可以看出,对系统中参数a,b分别增加25%或减小25%,逆优化控制方法都可以将系统控制到稳定的周期运动状态. (ii)增加反馈增益控制.对系统中参数a,b的值分别减小20%,分析系统的运动状态,如图6所示. 图6 反馈增益控制系统的相图和时域图 对系统中参数a,b的值分别增加20%,分析系统的运动状态,如图7所示. 图7 反馈增益控制系统的相图和时域图 对系统中参数a,b的值分别减少21%,分析系统的运动状态,如图8所示. 图8 反馈增益控制系统的相图和时域图 对系统中参数a,b的值分别增加21%,分析系统的运动状态,如图9所示. 图9 反馈增益控制系统的相图和时域图 对比图6~9可以看出,对系统增加状态反馈矩阵的控制方法只对参数a和b变化量不超过20%的情况有效果,如果系统中参数a,b变化量超过20%,此控制方法便失去了作用.对图3~9分析可知,通过逆优化控制方法对分数阶金融系统进行控制,系统中的参数可以至少能承受±25%的扰动量;通过在原有系统中增加反馈增益矩阵的控制方法,可以使系统承受最大±20%的扰动量.可见,在这两种控制方法作用下,系统均具有一定的鲁棒稳定性. 混沌运动是出现在经济系统中的一种极其复杂的现象,是当前非线性经济动力学研究的一项重要内容.论文基于分数阶理论建立了一类分数阶金融风险模型,研究了系统在平衡点处的稳定性.稳定性分析表明该分数阶金融风险系统存在非常复杂的动力学行为,选择不同的参数配比,系统的运行状态完全不同.将混沌控制策略引入分数阶金融风险模型中,采用逆优化控制法和增加反馈增益控制法来对分数阶金融系统进行混沌控制,并通过数值仿真,比较了控制前后金融系统动力学行为,讨论了两种控制方法的鲁棒性,证明了控制方法的有效性,并且通过增加反馈增益系数,提高了系统的控制效果.2 分数阶金融风险系统平衡点稳定性分析
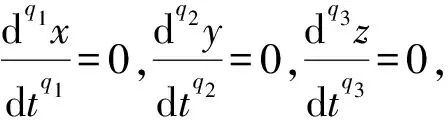
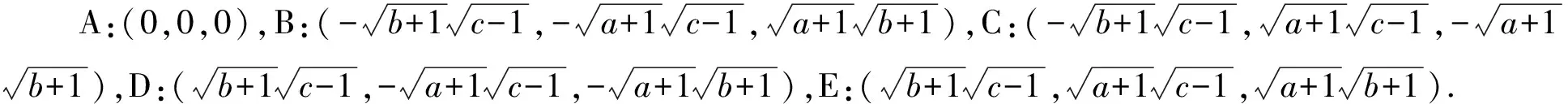


3 分数阶金融风险系统混沌控制
3.1 逆优化控制
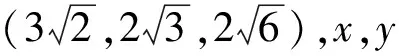
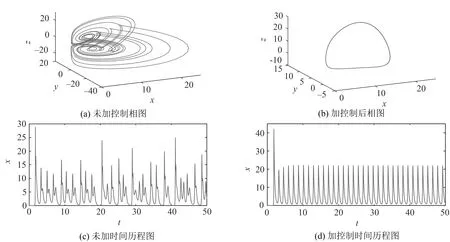
3.2 增加反馈增益控制
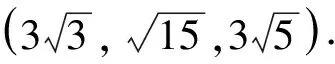
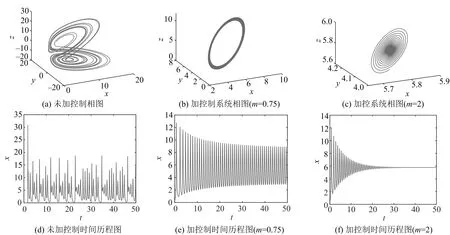
3.3 鲁棒稳定性分析

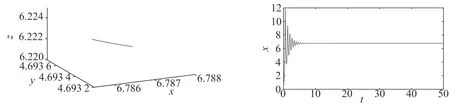
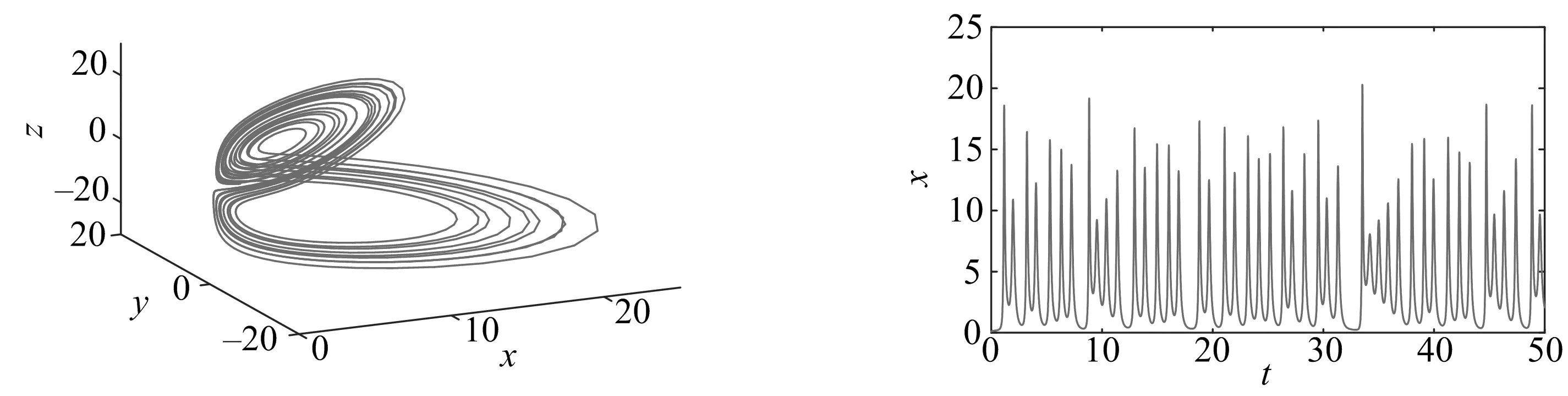
4 结束语
