对箭矩阵的两类广义逆问题

雷英杰，崔 萌

(中北大学 理学院，山西 太原 030051)

图的矩阵的广义逆特征值问题在物理方面具有许多实际应用价值，如量子力学、控制理论等方面，已经成为现代科技领域不可或缺的研究工具.在过去的几年中“构造伪雅可比矩阵的问题”吸引了许多学者的注意，并开展了系列研究，取得了显著的研究成果[1-10].

论文基于上述成果并针对图1对应的矩阵开展研究.

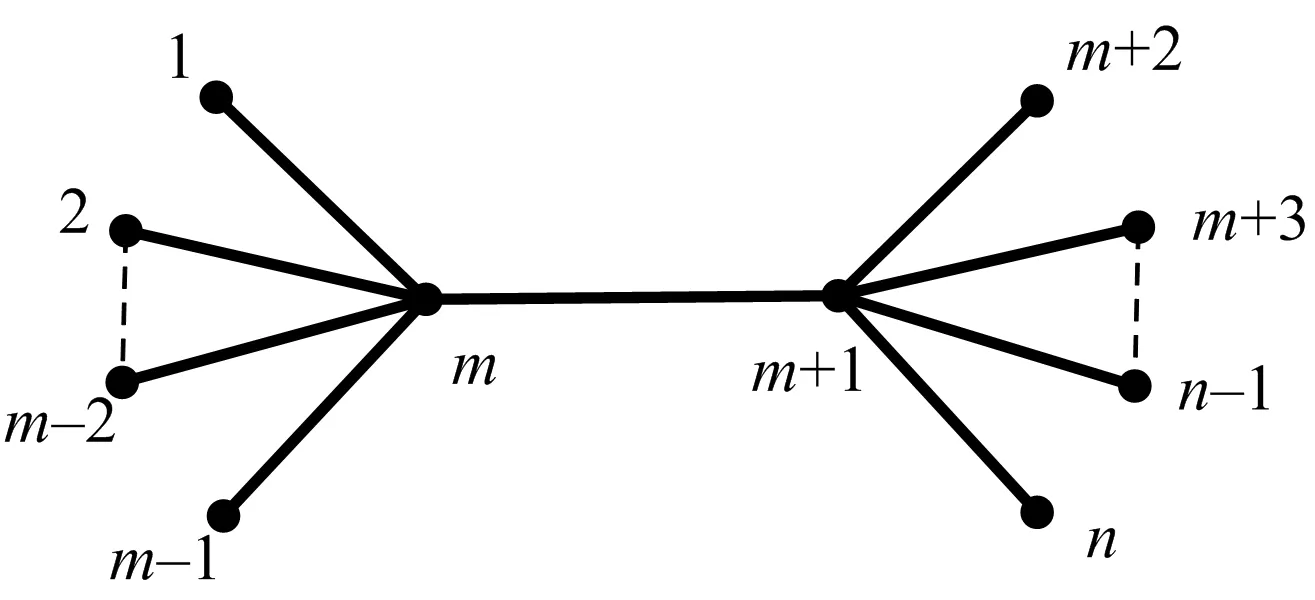
图1 矩阵的图

1 预备知识及问题

论文针对图1对应的形如(1)，(2)式的矩阵开展研究.

(1)

(2)

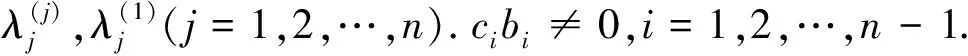
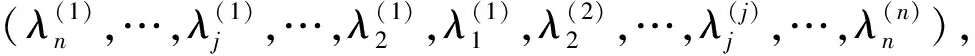
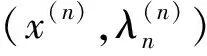
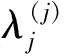
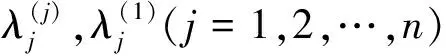
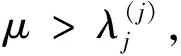
引理3形如(1)的矩阵T的主子矩阵对应的特征多项式满足

(3)

引理4形如(2)的矩阵A的主子矩阵对应的特征多项式满足

(4)

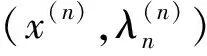
(5)

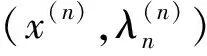
aixi+bixm=λxi,i=1,2，…,m-1,

c1x1+c2x2+…+cm-1xm-1+amxm+bmxm+1=λxm,

cmxm+am+1xm+1+bm+1xm+2+…+bn-1xn=λxm+1,

ci-1xm+1+aixi=λxi,i=m+2,…,n，

联立上式，推得结论.证毕.

2 问题1的解

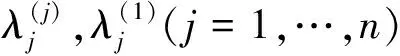
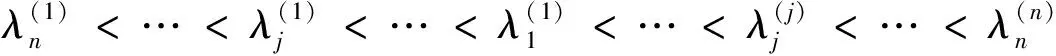
当j=m时，有

即

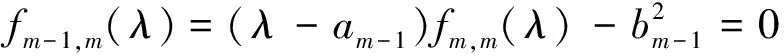
(6)

(7)

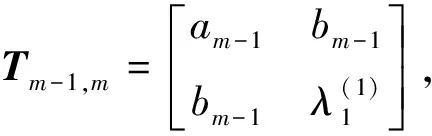
当j=1,2，…,m-2时，有

即

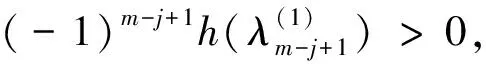
(8)

(9)

其中

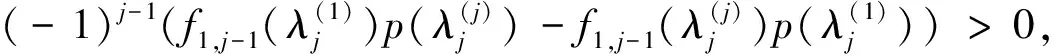
(10)

(11)

当j=m+2时，同理，有

(12)

(13)

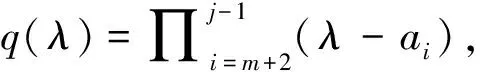
(14)

(15)

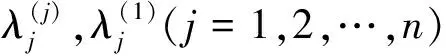
成立.证毕.

3 问题2的解

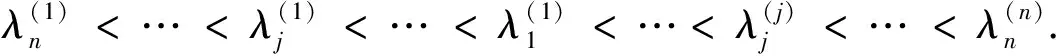
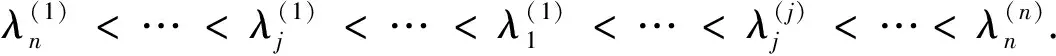
(16)

(17)

(18)

(19)

(20)

(21)

根据(5)式的公式变形，可以具体求得cj(j=1,2，…,n-1)和bj(j=1,2，…,n-1)的值.

(22)

(23)

(24)

(25)

(26)

(27)

(28)

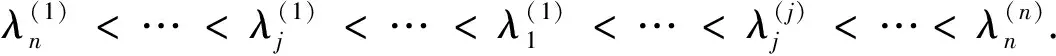
4 数值算法与实例

4.1 数值算法

以上定理1，2的证明过程即为矩阵T和A的构造过程，得到如表1的数值算法.

表1 数值算法

4.2 数值实例

给定实数-9<-8<-7<-6<-4<-3<1<2<3<4<5<6<7，构造形如(1)式的对箭矩阵.

解根据4.1的算法1，通过Matlab R2016a计算得到唯一矩阵

通过计算T7的主子矩阵的特征值如下：Λ(T3,3)={1.000 0}，Λ(T2,3)={2.000 0,-3.000 0}，

Λ(T1,3)={3.000 0,-2.000 0,-4.000 0}，Λ(T1,4)={4.000 0,-2.000 0,-2.714 3,-6.000 0}，

Λ(T1,5)={5.000 0,2.592 3,-2.000 0,-3.306 5,-7.000 0}，

Λ(T1,6)={6.000 0,2.741 8,1.900 7,-2.000 0,-3.549 6,-8.000 0}，

Λ(T1,7)={7.000 0,2.817 7,1.928 4,1.780 3,-2.000 0,-3.679 0,-9.000 0}.