分形理论在矿产资源勘查领域的应用研究进展*

崔中良，郭心雨，杨睿昕

(江西应用科技学院，江西 南昌 330100)

0 引言

2022年10月2日，习近平总书记在给山东省地矿局第六地质大队全体地质工作者的回信中指出，矿产资源是经济社会发展的重要物质基础，矿产资源勘查开发事关国计民生和国家安全。近年来，我国经济发展已由高速增长阶段转向高质量发展阶段，虽然资源需求量增速逐渐放缓，但需求总量仍保持高位[1]。受全球新冠肺炎疫情复杂多变、国际贸易保护主义抬头和霸权主义战略压制等影响，我国矿产资源安全形势面临严峻挑战[2]。因此，推进勘查理论创新、加强国内地质找矿研究具有十分重要的现实意义。自MANDELBROT提出分形概念[3-4]以来，分形理论逐渐成为非线性学科的前沿，并广泛应用于非线性系统的研究。分形理论基于数学方法从分维视角研究和揭示复杂自然现象中隐藏的规律性、层次性和标度不变性，能够刻画局部与整体、微观与宏观、离散与连续等关系。在矿产资源勘查工作中，分形理论已被应用于断裂控矿规律研究[5-8]、矿床分布规律研究[6,9-11]和地球化学勘查[12-14]等方面。

基于此，本文对上述研究成果进行了归纳总结，概述了分形理论在矿产资源勘查中的应用进展，并对其发展趋势进行了展望，以期为分形理论在实际勘查工作中的应用提供借鉴。

1 分形理论概述

1.1 分形的定义

MANDELBROT[3]在对海岸线长度进行研究时，首次提出了分形的概念，认为自相似性是分形的重要特征；随后给出了分形的数学定义[4]，简述如下。

设集合F⊂Rn的Hausdorff维数是DH，若F的Hausdorff维数DH严格大于其拓扑维DT，即DH>DT，则称集合F为分形集，简称分形。该定义的数学表达式可记为

F={DH∶DH>DT}。

鉴于这一定义具有不完备性，Falconer给出的定义被大多数学者所接受[15]。Falconer认为分形集合F具有如下典型性质：

a.F具有精细结构，即有任意小比例的细节；

b.F是如此不规则，以致其局部和整体都不能用传统的几何语言来描述；

c.F通常有某种自相似的形式，可能是近似的或是统计的；

d.一般地，F的分形维数大于其拓扑维数；

e.在大多数情况下，F可用非常简单的方法定义，由迭代产生。

需要强调的是，分形可分为规则分形(确定性分形)和无规则分形(统计分形)两类。规则分形常见于康托集合、科契曲线、谢尔宾斯基垫片等，而地质现象中的分形绝大多数属于无规则分形，只具有统计意义上的自相似性。

1.2 分维值

在分形理论中，分维值是对研究对象空间占有规模及复杂程度进行精确量度的工具。因研究对象、研究目的等的不同，学者采用的求解分维值的方法也不尽相同，主要有改变观察尺度求分维值、根据密度相关函数求分维值、利用分布函数求分维值、频谱法求分维值、根据测度关系求分维值、重整化群方法求分维值等，由此产生了不同类型或称呼的分维值，如容量维、信息维、关联维、矿床数量分布分维值、矿床密度分布分维值等。

2 分形理论在断裂控矿规律研究中的应用进展

断裂构造不仅是成矿热液的运移通道和矿体就位的赋存空间，也是矿质活化迁移的影响因素。尤其是在热液矿床中，断裂构造对于成矿尤为重要。断裂系统的空间分布十分复杂，传统的断裂研究中大多采用定性描述，而有关断裂与成矿关系的研究也以定性评价为主[16]。分形几何学可以实现对断裂构造复杂程度的定量表征，这为断裂与成矿关系的研究提供了崭新的视角。断裂分维值的计算方法及步骤见文献[16-17]。

断裂分维值与地质体连通性相关，且存在一个断裂分维临界值(1.22～1.38)[18]，即断裂分维值大于断裂分维临界值时，地质体的连通性较好，有利于成矿元素的活化及成矿流体的运移、聚集[16,19-21]。分形计算时，研究区尺度与构造规模相匹配，因此计算的整体断裂分维值与断裂分维临界值的比较可以在一定程度上说明研究区整体成矿构造条件的优劣。然而整体断裂分维值的计算仅能实现成矿潜力区或成矿有利区的粗略预测，因此当前大多数学者开展断裂分形研究时均对研究区划定分区，并基于分区分维值与分区赋存矿床数量及规模的耦合关系确定成矿有利分维值区间，进而实现对成矿潜力区或成矿有利区的准确预测。当前对于成矿有利分维值区间的宏观认识尚有分歧，部分学者认为断裂构造的分维值越大，越有利于成矿。毛政利等[22]基于对个旧矿区东区断裂构造系统的分形研究，认为断裂构造的分维值越大越有利于成矿。廖家飞等[23]发现广西贺州水岩坝矿田内已知矿床(点)均位于较高分维值区域，认为分维值的高低与已知矿床(点)的分布具有耦合性。王正庆等[24]研究广东诸广地区断裂分形特征与铀成矿关系时发现，断裂分维值的大小和矿床(点)的疏密呈良好的正相关性。还有学者认为断层系统处于临界分维状态下最有利于成矿。丁式江[25]通过离散元方法(UDEC)模拟了同一应力条件下变形后断裂的分布特征，结果显示：当断裂分维值增大到临界状态时，变形及渗透率突然增加，流体产生局域化分布；而当断裂分维值超过临界状态时，变形及渗透率继续增加，但流体的局域化分布消失。孙涛等[5]认为成矿概率与分维值并非简单的线性关系，且当分维值处于临界状态时，成矿流体易汇聚成矿。王维等[26]在对藏南扎西康矿集区断裂构造的分形研究中发现断裂分维值过大或过小均不利于形成较好的铅锌等金属矿化。实际上，断裂分维值表征地质体的连通性，从这个意义上来讲有利于矿床分布的区域应满足两个条件[7,11,17]：本身分维值较高，有利于成矿流体流通、渗透；邻区分维值较低，有利于成矿流体的封闭、沉淀。笔者在研究黔西北垭都—蟒硐成矿带断裂分形结构时发现，断裂容量维和信息维的联合应用对确定成矿有利分维值区间具有较好的效果(见图1)。从图1可以看出，黔西北垭都—蟒硐成矿带中赋存中—大型铅锌矿床的分区分维值区间较窄，分维值较高，铅锌矿床有利分布区为容量维大于1.58、信息维大于1.42的地区。

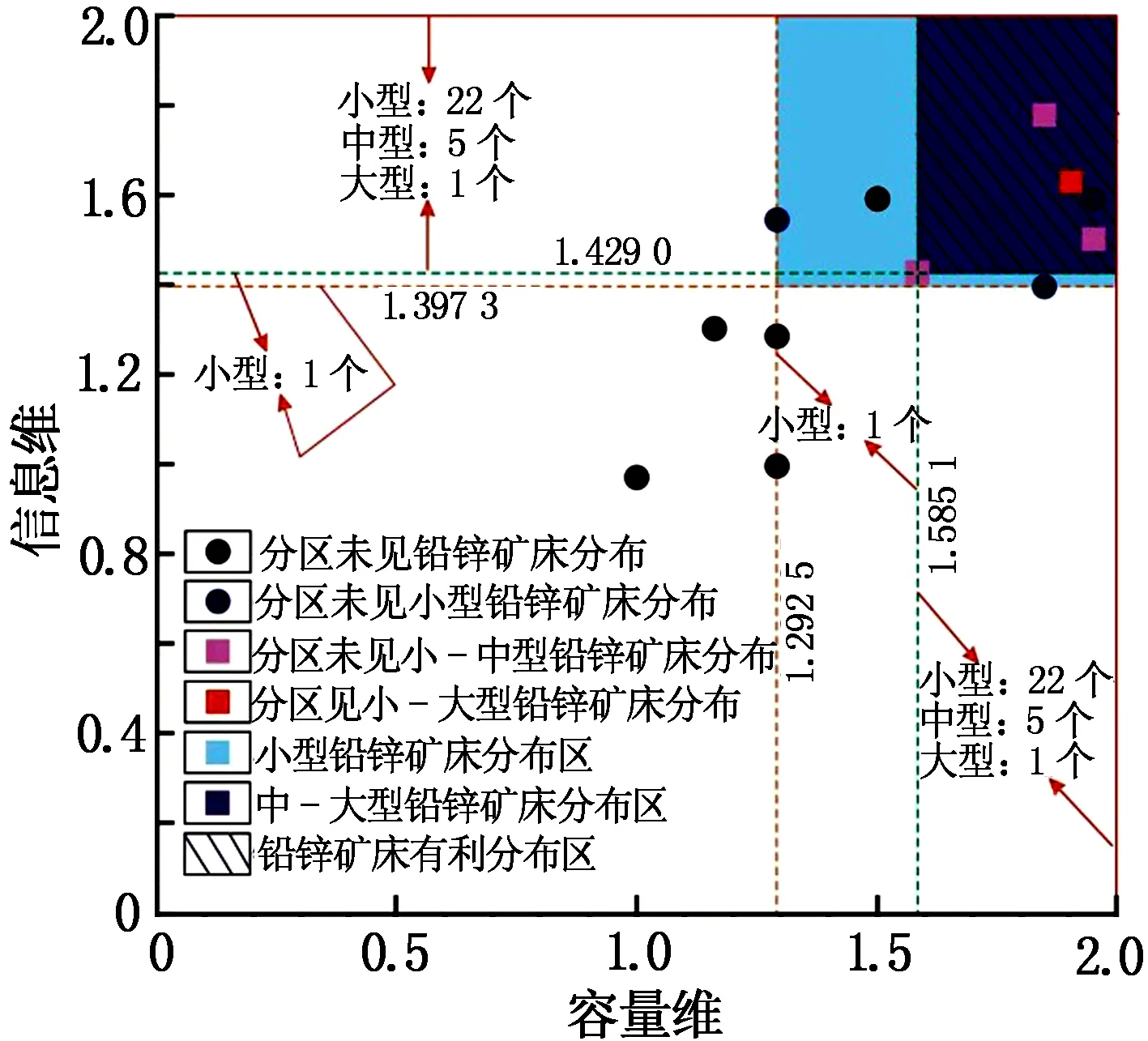
图1 黔西北垭都—蟒硐成矿带分区分维值与矿床发育规模、频数关系图[17]

3 分形理论在矿床分布规律研究中的应用进展

近年来，分形理论在矿床分形丛集分布规律研究中的应用相对较少。矿床分形丛集分布主要是由分形热液体系的活动所致[27]。具有自相似性的丛集分布，在无标度区内，事件之间相互关联[28]，与随机分布明显不同(见图2)。分形理论在矿床分形丛集分布规律研究中主要涉及矿床容量维、矿床数量分布分维值、矿床密度分布分维值和多重分形等计算，计算方法和步骤见文献[6,11,28-29]。谢焱石等[30]计算得出华南热液铀矿床容量维为1.025 4，明显小于江南地洼区和东南地洼区的断裂容量维，认为造成断裂与矿床分形差异的主要原因是矿床受断裂控制，且断裂发育演化过程具有复杂性。施国栋等[6]在开展安徽省矿点分布与主要形迹相关性的分形研究时发现，安徽省的矿产资源分布受长江水系影响明显，且分维值在1.3～1.4的水系有利于成矿。崔中良等[11]通过计算豫西熊耳山矿集区矿床(点)容量维、数量分布分维值和密度分布分维值后发现，研究区矿床(点)的丛集性较高，找矿前景较好。韩喜彬等[10]研究华南云开隆起西、北缘金银矿床的空间分形特征时指出，矿床容量维和矿床密度分布分维值可以作为矿床分布、矿化强度和聚集的定量指标。谭凯旋等[29]认为新疆阿尔泰地区矿床为多重分形分布，且其原因主要是矿床勘探研究程度较低及在不同尺度下矿床形成控制机理不同。通过矿床数量分布函数或矿床密度分布函数理论上可以预测已知矿床一定距离范围内未知矿床的潜在数量，因此分形理论对在具有相同成矿地质背景的区域(成矿带或矿集区)开展矿床分布规律研究具有很大的应用前景。

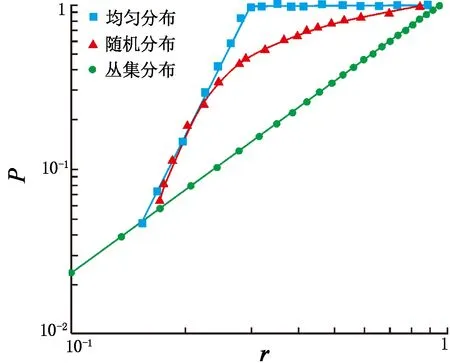
图2 分形丛集分布与随机分布和均匀分布对比示意图[28]

4 分形理论在地球化学勘查中的应用进展

地球化学勘查是预测找矿靶区最常用的方法之一，正态分布或对数正态分布是传统地球化学元素数据分析的理论基础。然而地球化学元素的分布具有随机性、自相似性、不连续性、混沌性、临界性和突变性等高度非线性特征[31-32]，传统的统计方法无法有效提取隐藏的非线性动力学相关信息[33]，异常解译常缺少明确的地质意义[34]。多重分形既可刻画在均值附近具有正态分布或对数正态分布的正常值，又能刻画两端具有幂律分布或分形长尾分布的异常值[35]，因此在识别和确定地球化学异常方面得到了广泛应用。地球化学勘查中应用的多重分形分析方法主要基于空间域、频率域、沃尔什域、小波空间、瓦尔氏空间和特征空间等建立，主要有C-A(含量/密度-面积)分析法、S-A(能谱密度-面积)分析法、ACAF(面积校正累计频率)分析法、C-D(含量/密度-距离)分析法、小波极大模分析法、W-A(能谱密度-面积)分析法、N-λ(能谱密度-特征值)分析法和LSA(局部奇异性指数)计算法等，相关计算步骤见文献[36-43]。

在各方法中，C-A分析法、LSA计算法和S-A分析法具有较强的普适性，应用最为广泛和有效[44]，因此本文着重介绍这3种方法。C-A分析法由CHENG等[36]在1994年提出，该方法体现的是空间域中成矿元素异常面积随含量/密度变化的自相似性，其定量刻画了成矿元素超常富集规律异常结构，并具有定量计算异常阈值的能力，可有效区分地球化学“异常”与“背景”[36]，被认为是开启了采用分形原理圈定地球化学异常的先河[35]。向中林等[14]基于新疆博罗科努成矿带东段水系沉积物样品中示矿元素的C-A分形模型，划分了地球化学背景、区域异常与局部异常，并结合乘积综合异常圈定了与区内已发现矿床的分布高度吻合的预测靶区。柯贤忠等[45]应用C-A分析法定量描述了西藏班戈地区8种微量元素的分形特征，并结合研究区地质矿产特征，探讨了这8种元素的成矿潜力。邹林等[46]通过C-A分析法探讨了青海阿尔茨托山地区元素成矿富集规律和空间分布特征，并划分了地球化学背景和异常，经检验对比，证明了该方法的有效性和实用性。上述应用研究证明C-A分析法在地球化学异常的识别中具有较高的准确性，然而在其实际应用中亦存在低弱异常难以提取、异常面积圈定较大、局部异常值点严重偏离等缺陷[47-49]。

在C-A分析法的基础上，CHENG等[37]提出了S-A分析法和LSA计算法[42,50]。奇异性是指在“极小”时间或空间尺度上产生“极大”物质或能量的异常，奇异性程度采用奇异性指数度量[50]。局部结构的定量化有助于为异常识别提供新的线索[51]，而局部奇异性指数模型能突出内蕴的弱异常及叠加异常[52-53]，还可作为一种有效的尺度不变性的高通滤波方法，因此常被用来度量奇异性地质现象的分布规律。局部奇异性指数是度量元素富集强度的定量参数，若奇异性指数大于2，则表示元素相对富集，小于2则表示元素相对贫化。为更准确、有效地度量元素的富集强度，LIU等[54]提出了局部奇异性-分位数方法，ZUO等[55]提出了一种改进的奇异性指数估算法。成秋明等[51]基于微量元素局部奇异性指数编制了地球化学异常图，结果表明，这些异常位置与多数矿床空间分布吻合，说明局部奇异性分析方法可以削弱背景值对异常圈定的影响，从而突出局部异常。ZUO等[55]提出了奇异性映射技术，并结合实例验证了这个算法的优越性。YUAN等[56]基于不同插值方法的效果对比，认为奇异性指数法比普通克里格法具有更强的鲁棒性和更好的效果。朱平平等[57]基于局部奇异性-分位数方法发现元素富集的空间位置与胶东毕郭地区已发现的金矿床有较好的对应关系，认为局部奇异性方法能够较好地指示矿床潜在的形成位置。

S-A分析法是一种建立在傅里叶空间进行异常和背景分解的分形滤波技术，体现的是频率域中功率谱密度(S)与功率谱密度高于S的面积(A)的幂律关系，其通过构建不同类型分形滤波器实现对复杂模式的识别，具有压制背景、突出局部弱小异常信息的特点[13,37]。S-A分析法能够度量时-空复杂模式的广义自相似性，还可以形成基于不同广义自相似性的分形滤波技术[47]。AFZAL等[58]基于伊朗中部斑岩型铜矿2 709个土壤样品，利用S-A分析法识别了地球化学异常。刘世宝等[49]对青海柴北缘地区1∶20万区域的地球化学数据进行处理后发现，S-A分析法能够较好地排除背景场并压制干扰因素，从而突出弱小异常。韦导忠等[59]利用S-A分析法对皖东张八岭-管店地区深部土壤中Au元素地球化学场进行了异常识别，结果显示，该方法能够有效分离地球化学背景。毛先成等[60]在采用S-A分析法开展胶西北金矿集区地球化学异常识别和资源潜力评价研究时发现，超过92%的已知矿床(点)落在提取的地球化学异常高值区，说明了S-A分析法在胶西北金矿集区应用的可靠性。成秋明[35]基于云南兰坪-金顶地区水系沉积物地球化学数据开展了成矿预测，采用S-A分析法有效消除了复杂背景及玄武岩干扰的影响，圈定了找矿靶区，后经勘探发现了五宝山、菜子地矿床。

5 其他应用

分形理论除了在断裂控矿规律研究、矿床分布规律研究和地球化学勘查中得到应用外，亦在遥感蚀变异常信息提取[61]、资源量分布规律表征[17]、品位变化特征对矿化强度的刻画[33]、含矿脉体形态分析[62]和油气资源储层评价[63]等研究中得到了应用。蚀变岩石与正常围岩因成分不同，在遥感图像上体现为像元亮度的差异，刁海等[61]基于分形模型开展了遥感灰度异常提取研究，结果显示提取的铁染异常与黑龙江多宝山地区断裂构造、已知矿点吻合度较高。崔中良等[17]采用频数-大小分形模型对黔西北垭都—蟒硐成矿带铅锌矿床资源量的丛集性进行了定量表征。定量刻画成矿元素品位的变化特征有助于深入理解成矿过程，万丽等[33]运用多重分形去趋势移动均值(MFDMA)法对云南普朗斑岩型铜矿床钻孔中Cu品位开展了多重分形研究，发现多重分形强度随矿化强度等级的减弱而增加。脉体分形能够揭示脉体的连通性和生长规律，李柱等[62]基于内蒙古维拉斯托含矿石英脉脉厚分形特征和品位分形特征探讨了含矿石英脉形态分带的成矿动力学机制。致密砂岩储集层微观孔喉结构与其储集能力和微观渗流特性密切相关，岳亮等[63]基于分形理论对四川盆地广安地区须家河组六段致密砂岩开展了储层物性及非均质性特征研究，结果较好地显示了分形维数与孔隙度、渗透系数之间的关系(见图3)。

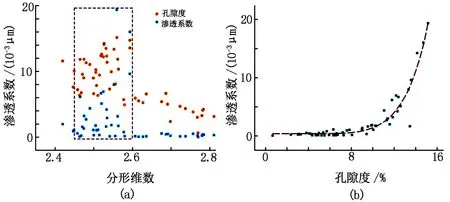
图3 广安地区须家河组六段砂岩储集层分形维数、孔隙度与渗透系数的相关性[63]

6 展望

在无标度区内，地质现象具有统计自相似性，因此局部与整体的结构可以互相推测，这对资源勘查具有非常重要的意义。当前分形理论在资源勘查领域取得了较多的研究成果，优势十分明显。而目前分形理论主要被应用于断裂控矿规律研究、矿床分布规律研究和地球化学勘查等方面，学者们建立了一系列分形分析模型。每种分形分析模型均具有一定的适用范围，针对单一地质体开展的单一分析方法会受分形模型的局限，有时效果不佳，而为了提高研究成果的准确性和有效性，未来分形理论在资源勘查领域的实际应用可能会以“多种分形方法联合使用”和“分形方法结合其他方法联合使用”为主。崔中良等[64]基于赣南兴国—宁都成矿带断裂构造、萤石矿床的分形结构特征及两者之间的耦合关系，探讨了重点成矿与找矿区域。朱平平等[57]对胶东毕郭地区Au元素数据依次应用局部奇异性→局部奇异性-分位数→Fry方法，进行了定量表征和优选方位的确定。蒋超等[8]对广西大瑶山西北地区开展了断裂分形及矿床Fry分析，并圈定了成矿预测靶区。综上，分形理论未来在资源勘查领域的应用将会愈加成熟和广泛。