铁路集装箱旅客化运输系统日常工作计划研究

宋浚哲

(中国铁路经济规划研究院有限公司 运输研究所，北京 100038)

0 引言

为解决传统运输组织模式集装箱运输时效性差等问题[1]，余永金等[2]提出在既有铁路站场布局的基础上采用“动箱不动车”的模式，提高集装箱运输效率。魏玉光等[3]则提出建立集装箱旅客化运输系统，仿照旅客列车模式，设置旅客化列车，将集装箱装卸作业前置化，直接在站台完成装卸作业，压缩集装箱在站作业时间。装卸作业完毕后，集装箱列车在到发线直接组织发车，与传统运输组织模式相比，集装箱旅客化运输系统具有以下特点：一是集装箱列车在运输全流程中不进行解编作业，采用固定车底，因而，集装箱列车不进入编组站作业，能够缩短箱流在始发站的等待时间，同时，集装箱列车各箱位在运输全程中可能存在空置；二是集装箱装卸设备前置化，集装箱列车在到发线完成装卸作业，装卸设备、集装箱卡车等设施设备应紧靠到发线。

集装箱旅客化运输系统的运输组织体系主要包括箱流预测、开行方案、运行图、车底运用计划、日常工作计划等，目前日常工作计划编制尚存在研究空白。在旅客运输中，列车开行方案、停站方案确定后，旅客能够根据实际需要调整出行时间，实现客流合理分配。与旅客运输不同，箱流不能实现自主分配。因此，日常工作计划应根据列车开行方案和停站方案，确定箱流分配方案。当运输需求发生波动时，及时调整箱流分配方案，达到合理分配箱流的目标。

为解决铁路集装箱运输组织不灵活的问题，日本铁路采用“E&S 模式”[4]，即待运集装箱放置在车辆上形成车组，列车到达车站后，在到发线进行车组摘挂。该方式实质上是将编组站作业提前至到发线，压缩在站作业时间。该模式下单次摘挂作业时间较为稳定，列车在站作业时间主要受车组数量限制。然而，日本铁路主要承担集装箱海铁联运任务，箱流流向较为单一；该作业模式需要占用多条线路进行车组暂存，摘挂次数多，对车站硬件水平及组织管理水平提出较高要求。因此，该模式难以适应中国铁路集装箱运输的实际需要。

集装箱旅客化运输系统与传统运输组织模式存在较大差异，集装箱旅客化列车仿照旅客列车运输模式，严格按图行车，开行方案需综合考虑运输需求、运输时效性。郭洪文[5]结合既有路网运输需求，综合考虑集装箱列车编成辆数、节点停站时间、旅行时间等影响因素，构建基于路网总箱时最小及箱位空驶率最低的双目标整数规划模型。夏阳等[6]采用自适应大邻域搜索策略，应用蚁群算法确定路网中快速集装箱列车运行径路及开行频率。Xia 等[7]研究开行方案确定情况下的列车停站方案，并以列车“上座率”为影响因素，提高集装箱列车经济性。

为提高运营效率，学者们针对列车停站、货流分配进行研究[8-10]，通过在目标函数中添加惩罚值，采用启发式算法获得货流分配方案。前述研究以箱流预测结果为基础，忽略实际运输组织过程中产生的需求波动，难以实现预期的最大效益。为提高作业计划可行性，黄鉴[11]以客运专线为研究对象，分析客流动态调整情况下的列车停站方案，建立和声搜索算法与模拟退火算法相结合的优化模型；刘欣萌[12]结合不同时段运输需求的差异，采用鲁棒性优化方法，建立需求变动环境下的货物快运网络模型。针对客货运需求波动性，江文辉等[13]以运输价格为衡量指标反映运输需求波动性，构建多列车运力分配和定价联合决策的混合整数概率非线性规划模型；冯建容[14]、宋佳[15]在停站方案中引入成本概念，旨在提升铁路企业经济性；李得伟等[16]以节点服务水平替代停站方案各项考虑因素，建立优化模型。

研究针对铁路集装箱旅客化运输系统组织体系中的日常工作计划编制问题，建立箱流分配模型。模型综合考虑运输需求波动性及箱流班次差异性，引入上座率不均衡性系数，确定列车间箱流分配方案。最后，研究结合连云港—阿拉山口国际联运通道实际运输需求进行案例分析，验证模型的有效性。

1 铁路集装箱旅客化运输系统日常工作计划优化模型

1.1 日常工作计划模式分析

在铁路运输组织过程中，路网中箱流情况、列车开行等与计划存在差异，车站需要根据前日作业情况、当日作业任务制定日常工作计划，使车站日常工作计划与长期工作计划相吻合。研究结合现有列车开行方案、列车停站方案以及箱流波动情况，调整箱流装载方案，建立铁路集装箱旅客化运输系统日常工作计划优化模型。

集装箱列车每个箱位类似于旅客列车的席次，研究引入列车上座率概念，借鉴旅客列车上座率定义，定义集装箱列车在某一区段内，实际载箱量与列车总箱位数间的比值为列车上座率，该指标用来测算集装箱列车能力利用情况。在箱流分配中考虑列车能力利用率的影响，不均衡的箱流分配方案将导致部分列车欠轴情况严重，无法达到列车开行标准，造成箱流延误。因此，模型的优化目标是运输能力冗余时，使各列车间列车上座率差异最小；运输能力不足时，总载箱量最大。在实际作业中，每日作业计划需要考虑前日作业对当日的影响，因而，模型考虑滞留箱流的影响，按批次进行箱流分配，提高运输组织精细化程度。

1.2 模型假设

模型中包含以下假设：①假设路网中各区段均为双线区段；②假设路网中各车站作业能力均满足要求；③假设箱流均为直达，无中转作业；④假设每个运输任务均整组运输，同一运输任务不进行拆分。

1.3 模型构建

1.3.1 目标函数

构建目标函数，旨在评判箱流分配水平。当路网实际箱流量小于预测箱流量时，全部箱流都将分配至普通列车，优化目标为使列车间上座率不均衡系数最小；当路网实际箱流量大于预测箱流量时，部分箱流将分配至虚拟列车，由于罚数M足够大，目标函数的值主要由虚拟列车载箱量决定，此时优化目标转化为虚拟列车载箱量最小。目标函数如下。

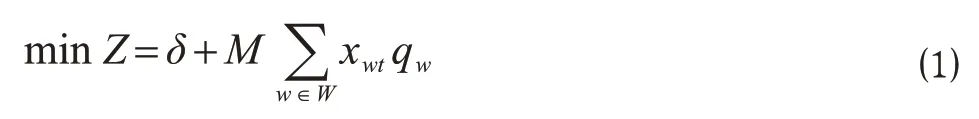
式中：Z为运输系统阻力值，表示运输系统中箱流分配水平，该值越小表示箱流分配越合理；δ为上座率不均衡系数，%，0 ＜δ＜ 1；W={w=(i，j，k)|i，j∈S;k=1，2}为箱流 OD 的集合，w为箱流 OD 的索引，i和j为路网中互不相同的车站，S为路网中车站的集合，路网中车站的数量为|S|，k为箱流批次的索引，批次1表示本日正常运输组织的箱流，批次2 表示前日延误箱流；xwt为0-1 变量，当列车t担当箱流w时，xwt=1，否则为0；qw表示箱流w的箱流量，qw＞ 0。

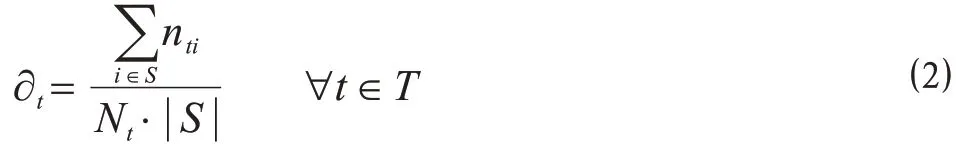
式中：∂t为列车t的平均上座率，为列车在区段内载箱量与列车最大载箱量的比值，%；nti为列车t在车站i的载箱量，TEU；Nt为列车最大装载能力，TEU；T={t|t=1，2，…，n}为列车集合，|T|为计划已确定开行的普通列车的数量，t为计划已确定开行的普通列车的索引；另外，定义一列虚拟列车m，其在路网中每站均停，且装载能力Nm为无限大，由此构建包含虚拟列车的列车集合。

由于列车在某一区段运行过程中载箱量不发生变化，区段起点站列车的载箱量即为区段载箱量，因而可以用列车在车站的载箱量计算列车平均上座率。在保证单列集装箱列车上座率的同时，减小列车间平均上座率的差异，有助于保证各列列车均能满足开行条件，并使列车在站作业时间稳定在一定范围内。

式中：βt为各列车上座率与列车间平均上座率之间的差值，%。

βt的值可正可负，在计算各列车βt之和δ时，可能出现抵消，影响计算准确性。因此，定义列车上座率不均衡系数θt如下。

公式(4)表示无论βt正负，θt均应不小于βt的绝对值，θt必为非负数。

此时目标函数可以转化为公式(6)。

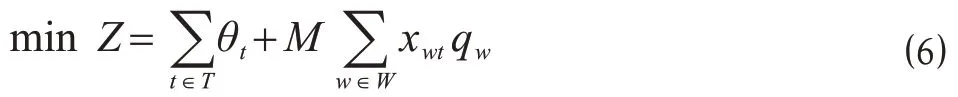
1.3.2 约束条件

（1）集装箱列车在各个区段的载箱量均应小于其最大装载能力，列车能力约束如下。

列车t在车站i的载箱量nti，TEU，包含在车站h之前及本站装车，且终到站为车站h以远的箱流。

（2）对于任意OD，有且只有一列列车担当运输任务，箱流装载约束如下。

（3）箱流w分配至列车t时，该列车的停站方案中应包括箱流w的起讫点，列车停站约束如下。

1.4 求解算法

公式(2)至公式(5)将目标函数线性化后，目标函数转化为线性函数。其中，公式(4)中θt需要在箱流分配方案确定后才可以求出。即未确定箱流分配方案前无法确定θt的取值，而无θt无法确定目标函数值，不能确定箱流分配方案，模型陷入循环，无法求解。研究按照以下步骤解决上述问题。

步骤1：根据列车数量，将各列列车的θt设定为自变量，其取值范围设定为[0，1]。

步骤2：将公式(4)作为约束条件引入模型。在开行方案确定的条件下，运输能力已知，则可以确定列车间平均上座率为定值。将公式(3)带入公式(4)，构成的新约束可以表示为：对于任意列车t∈T，其对应的θt应不小于±βt中的较大值。

步骤3：自变量θt满足步骤2 形成的新约束后，为使目标函数达到最小值，θt将在取值范围内取最小值，即使θt等于±βt中的较大值。由此，可以求得各列车上座率不均衡系数。

为保证集装箱运输的时效性，前日延误箱流应优先组织运输。为此，在目标函数设定中给予批次2 的箱流更高的优先级。设定批次1的箱流权重M1，批次2的箱流权重M2，其中，M1≪M2。由此，在模型迭代过程中，为使目标函数值最小，各列列车将优先满足批次2的运输需求。

2 案例分析

2.1 研究数据

根据《中长期铁路网规划(2016 调整)》，我国将建成以三级节点为核心的铁路集装箱运输网络。集装箱旅客化运输系统依托上述设施，改扩建形成一、二级节点。研究以中欧班列运输通道连云港—阿拉山口的11 个站点为例，连云港—阿拉山口运输通道示意图如图1 所示。11 个站点均为一、二级节点，运行列车均为快速集装箱列车。高运输需求条件下分批次表如表1 所示，设定运输能力低于运输需求，用以分析在运输能力不足条件下，模型能否使列车运输量最大，且保证延误箱流优先运输；低运输需求条件下分批次表如表2 所示，用以分析运输能力相对充足的情况下，集装箱任务在列车间的分配是否能够实现均衡。设定批次1 的箱流权重M1=10，批次2 的箱流权重M2=50。

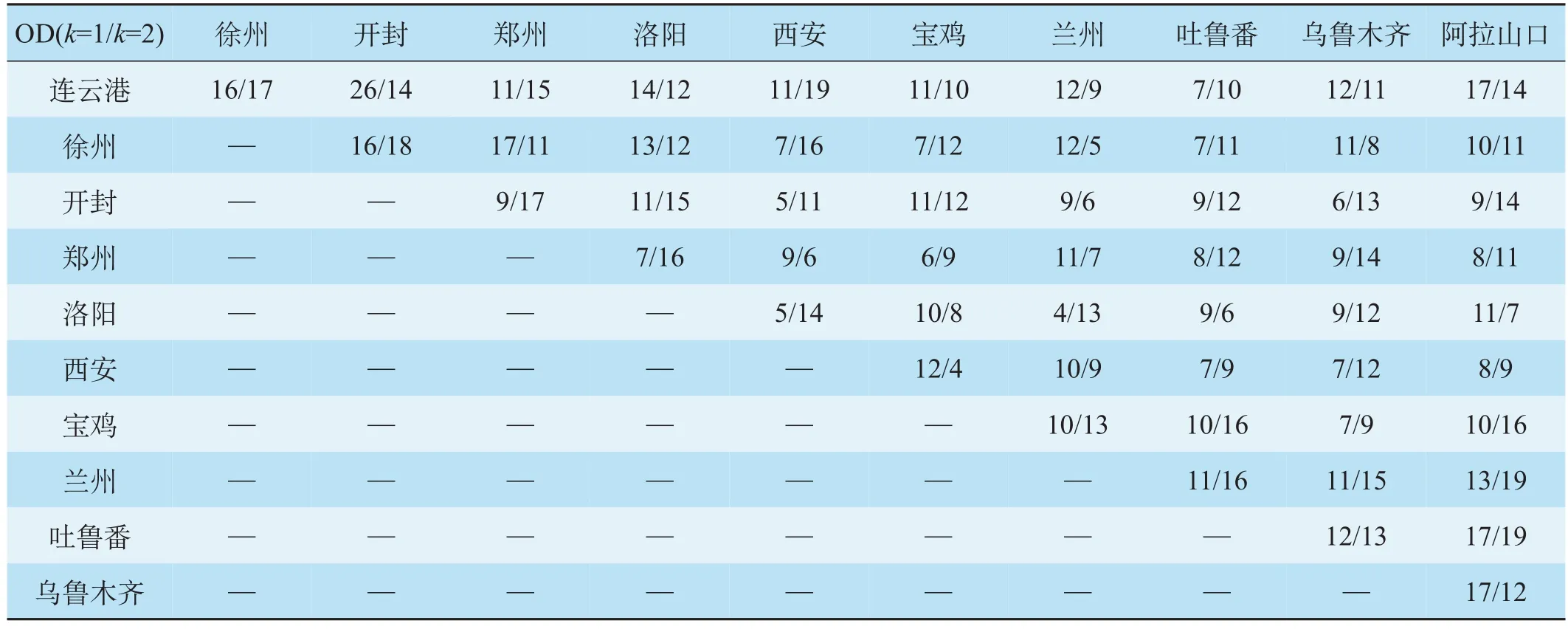
表1 高运输需求条件下分批次表 TEUTab.1 Batch under sufficient transportation demand

表2 低运输需求条件下分批次表 TEUTab.2 Batch under insufficient transportation demand

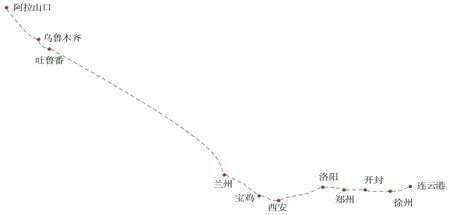
图1 连云港—阿拉山口运输通道示意图Fig.1 Lianyungang-Alashankou transportation channel

集装箱列车编组辆数、装载能力需要结合站场设备实际，综合考虑到发线长度、集装箱箱型、机车等因素。研究中设定集装箱列车编组辆数为50 辆；假设列车均装载20 ft 标准集装箱，即可确定列车最大装载能力为100 TEU。另外，列车开行方案及停站方案参考夏阳等[6]的计算结果，停站方案示意图如图2所示。

图2 停站方案示意图Fig.2 Stop schedule plan

2.2 计算结果

列车在高运输需求条件下箱流分配结果如表3所示。在全部110 个运输需求中，83 个运输需求得到满足，27 个运输需求由虚拟列车运输，分析箱流分配结果，批次1 集装箱均得到运输，即前日延误箱流全部完成运输。由于存在箱流不可拆分约束，列车上座率无法达到100%。高运输需求条件下目标函数最优值为2 401.292，部分箱流由虚拟列车运输。高运输需求条件下列车在各区段载箱量如表4所示，表4 分析列车在各个区段的载箱情况。其中，列车1 在吐鲁番—阿拉山口区段能力冗余；列车2 在连云港—徐州、乌鲁木齐—阿拉山口区段存在能力冗余；列车3 在西安—阿拉山口区段能力冗余；列车4 在连云港—开封、乌鲁木齐—阿拉山口区段存在能力冗余。由于列车能力冗余分布较为分散，仅适用于中短途箱流运输。在案例研究中，列车1 在徐州—吐鲁番区段、列车2 在徐州—乌鲁木齐区段，列车3 在连云港—西安区段、列车4 在开封—洛阳、西安—乌鲁木齐区段存在能力瓶颈，影响其他箱流的运输。

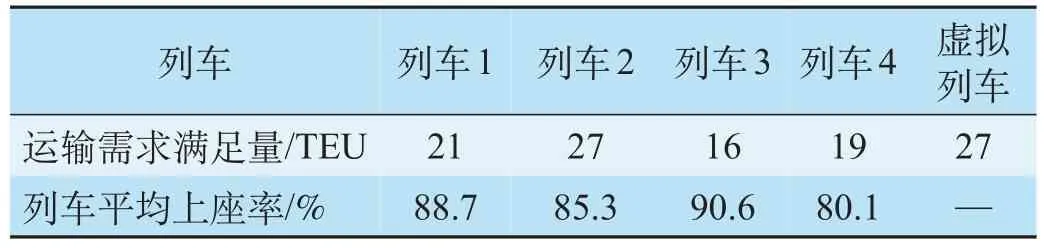
表3 高运输需求条件下箱流分配结果Tab.3 Distribution result of container flow under sufficient transportation demand

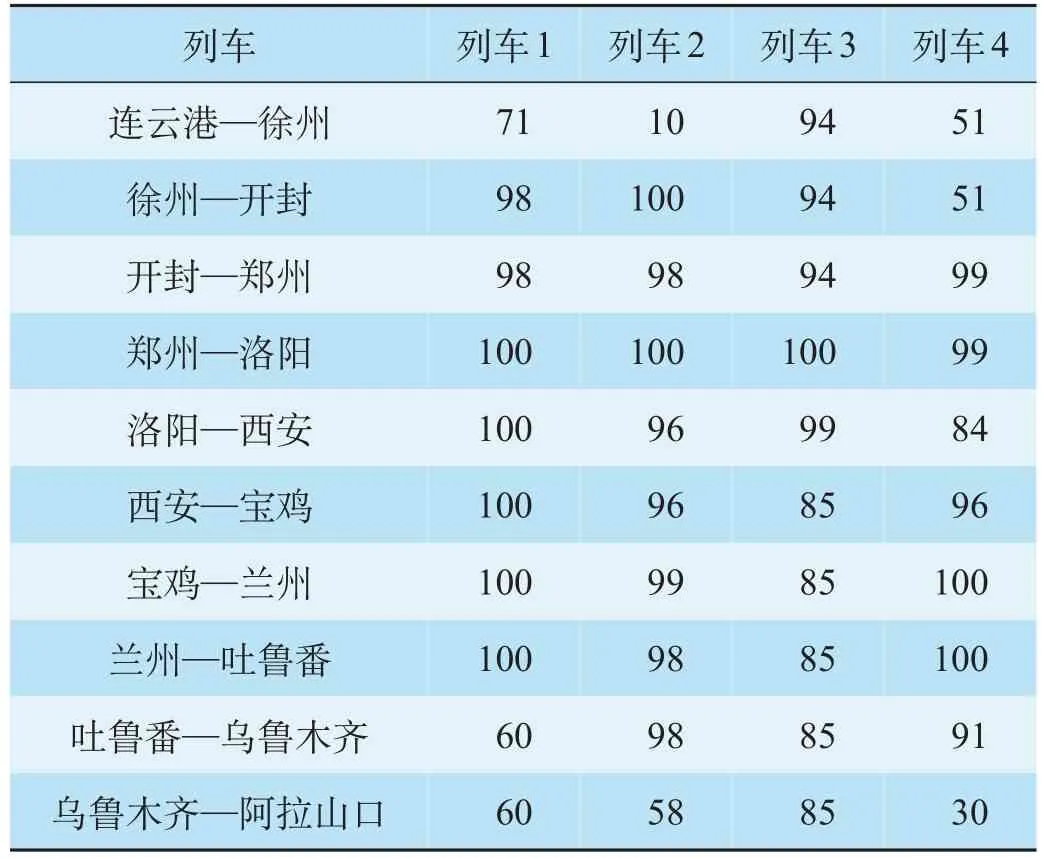
表4 高运输需求条件下列车在各区段载箱量 TEUTab.4 Container distribution scheme under sufficient transportation demand

列车在低运输需求条件下箱流分配结果如表5 所示。经计算，低运输需求条件下目标函数最优值为0.058，即上座率不均衡系数为0.058，表明在低运输需求条件下，所有箱流均可以由普通列车运输，箱流在列车间分配较为均衡。在实际作业中，列车开行方案在一段时间内固定，但车站出于节省到发线能力的考虑，将禁止开行载箱量过小的列车，进而影响箱流运输。因此，在箱流不足的情况下使列车上座率相对均衡具有实际意义。低运输需求条件下列车在各区段载箱量如表6 所示，列车在各个运输区段内存在较大的能力冗余。

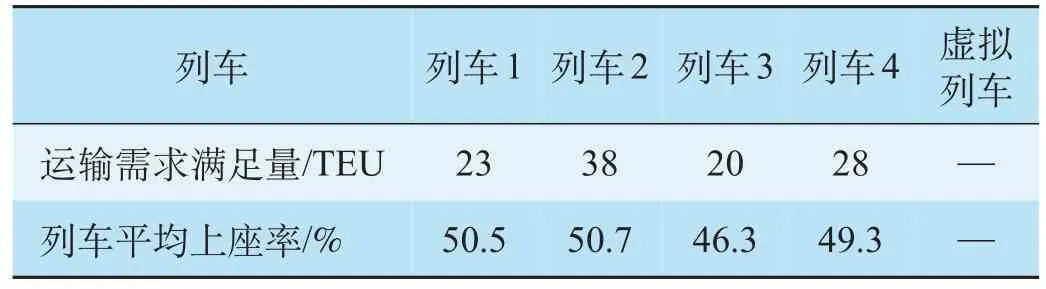
表5 低运输需求条件下箱流分配结果Tab.5 Distribution result under insufficient transportation demand

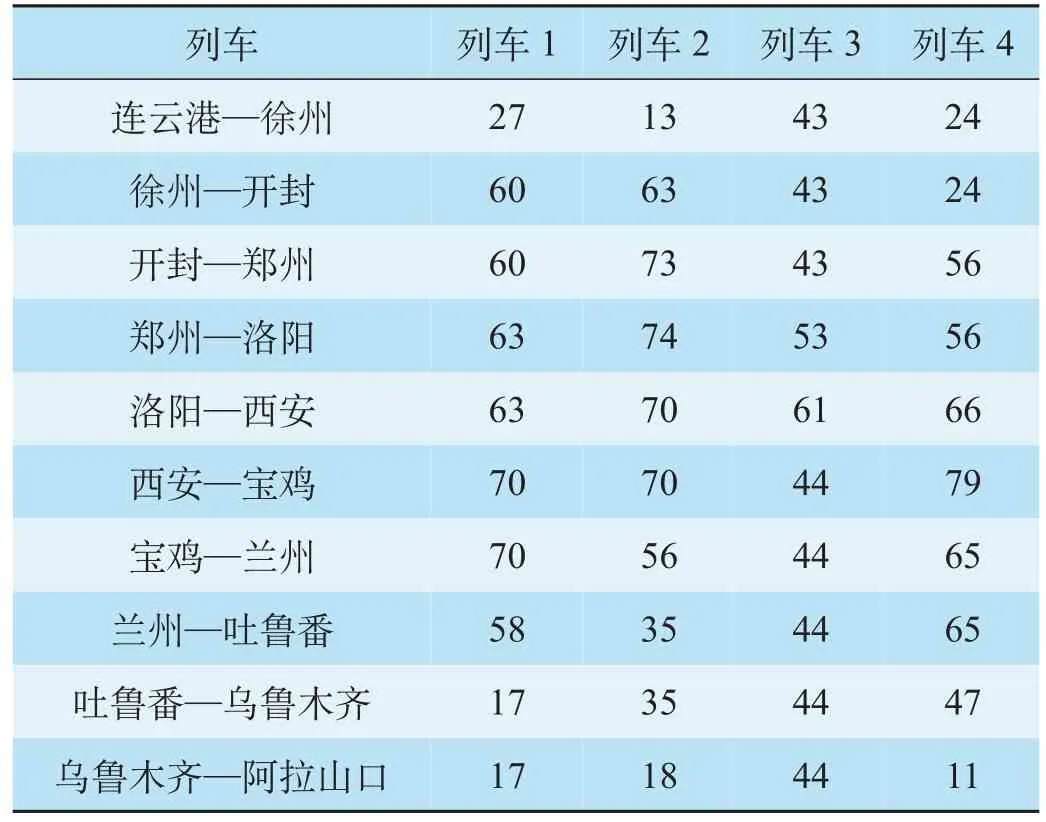
表6 低运输需求条件下列车在各区段载箱量 TEUTab.6 Container distribution scheme under insufficient transportation demand

3 结束语

研究综合考虑铁路实际运输组织过程中箱流波动情况，建立铁路集装箱旅客化运输系统日常工作计划优化模型。当运输需求超过运输能力时，模型以箱流运输量最大化为目标，避免出现箱流延误；当运输需求小于运输能力时，模型以平衡箱流在各列车间的分配为目标，保证各列列车均满足列车开行条件。模型还引入批次概念，将前日延误车流与本日计划作业车流分组分配，优先运输前日延误箱流，避免出现箱流长期延误的情况。研究以连云港—阿拉山口通道为例，证明模型的有效性，综合分析不同运输需求条件下的日常工作计划方案。未来，还应将铁路集装箱两端集疏运作业引入日常工作计划构建中，进一步提高铁路集装箱旅客化运输系统整体效率；其次，结合车站作业能力、作业效率，进一步提高日常工作计划的协同性。