基于波形特征和决策树分类算法的岩体破裂信号识别
2022-11-22王培武皇甫风成陈天晓徐世达
龙 翼,王培武,皇甫风成,陈天晓,徐世达
(1.紫金矿业集团股份有限公司,福建 龙岩 364000;2.东北大学深部金属矿山安全开采教育部重点实验室,辽宁 沈阳 110819)
微震信号识别是开展矿山开采过程微震监测的基础。近年来,随着矿山开采深度增加和高强度开采模式的推广,采场(巷道)围岩破坏日趋凸显,严重时甚至会引起岩爆、冒落等灾害。谢和平等[1]国内学者指出在高应力条件下,岩爆已成为矿山岩体的重要灾害之一。目前,微震监测技术已被广泛应用于岩爆、大体积冒落等灾害监测。该技术利用岩体破裂时发出的弹性波来监测岩体的稳定性。但由于矿山施工环境复杂,爆破振动、大型用电设备干扰等因素导致微震监测系统接收到除岩体破裂外的多种干扰信号。因此,岩体破裂信号识别是开展岩体稳定性评估及破坏失稳灾害风险评估的前提。ALLMANN等[2]提出了一种基于P波波谱与震源模型均方根拟合差的爆破信号与岩体破裂信号识别方法;朱权洁等[3]基于小波分析和分形理论提出了现场微震监测信号识别方法;MALOVICHKO[4]引入地震学信号识别技术,考虑发生时间、辐射模式、低频带与高频带能量分布和相邻波形相关系数特征参数,采用最大似然法对岩体破裂波形进行识别;VALLEJOS等[5]采用逻辑回归与神经网络建立了基于震源参数的高精度微震事件识别模型;ZHAO等[6]采用频率切片小波变换技术分解信号的方法,对两类信号不同的能量分布特性进行了对比研究;SHANG等[7]通过经验模态分解和奇异值分解进行波形特征提取与波形分类,识别准确率能够达到88.25%;ZHANG等[8]提出了基于变分模态分解的微震信号特征提取及分类辨识方法;罗小燕等[9]提出了一种基于改进变分模式分解算法(VMD)和GA-BP神经网络的预测方法,提取信号能量特征参数作为模型的输入构建GA-BP预测模型,准确率达90%;XU等[10]建立了岩体破裂信号神经网络识别模型,有效剔除了现场噪音信号的干扰。
本文针对阿舍勒铜矿微震监测系统采集信号,分析阿舍勒深部采区不同类型波形特征参数差异,开展波形特征参数与波形类型相关性分析,建立决策树算法波形识别模型,实现阿舍勒铜矿微震监测岩体破裂波形自动识别,减少微震数据处理人工工作量,提高岩体破裂信号识别精度,消除噪音信号的干扰。
1 决策树算法
决策树算法是监督学习中的一种,常被用来解决回归和分类问题[11]。“完全生长”的决策树因为结构简单直观,具有很强的解释性,已被广泛应用。一棵完整的决策树包含特征选择、决策树构建、剪枝三个过程。
常用的决策树算法主要有ID3、C4.5、CART等。ID3算法核心是在各个节点上应用信息增益准则选择特征,构建决策树。ID3算法未进行剪枝,决策树的结构可能过于复杂,易产生过拟合问题。C4.5算法需要对数据进行多次顺序扫描和排序,效率较低。本文选用更适用于多变量组合决策的CART算法进行分类。
1.1 CART算法决策树生长
决策树中的CART算法生成的决策树是二叉树,每一次分裂会产生两个子节点,其主要由分类树的生成和剪枝处理组成。CART分类树预测分类离散型数据,使用基尼指数(Gini)选择最优特征,同时决定该特征的最优二值切分点。分类过程中,假设有k个类,样本点属于第k个类的概率为Pk,则概率分布的基尼指数定义为式(1)。
(1)
根据基尼指数定义,可以得到样本集合D的基尼指数见式(2)。
(2)
式中,Ck为数据集D中属于第k类的样本子集。
数据D根据特征A在某一取值a上进行分割,得到D1、D2两部分后,特征A下集合D的基尼系数见式(3)。
Gain_Gini(D,A)=
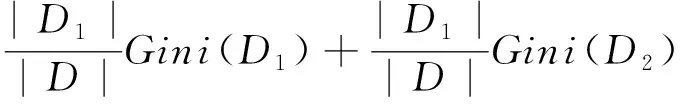
(3)
式中:Gini(D)为集合D的不确定性;Gini(D,A)为A=a分割后集合D的不确定性。基尼指数越大,样本集合的不确定性越大。
对于属性A,分别计算任意属性值将数据划分为两部分之后的Gain_Gini,选取其中的最小值,作为属性A得到的最优二分方案。然后对于训练集S,计算所有属性的最优二分方案,选取其中最小值,作为样本的最优二分方案,见式(4)和式(5)。
min(Gain_Gini(D,A))
(4)

(5)
1.2 决策树剪枝
剪枝是决策树学习算法中解决过拟合问题的主要手段[12]。思路是从已生成的分类树中剪掉一些子树或者叶子节点,并将根节点或者父节点作为新叶子节点,以便简化分类树模型。决策树剪枝往往是通过极小化决策树的整体损失函数或者代价函数。设树的叶子节点为|T|,叶子节点t上有Nt个样本点,其中k类的样本点数为Nkt,Ht(T)为结点t上的经验熵,α≥0,所以损失函数定义为式(6)。

(6)
经验熵为式(7)。
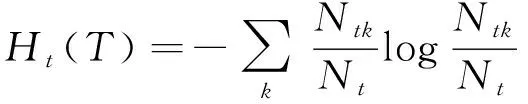
(7)
可得式(8)。
C(T)=C(T)+α|T|
(8)
式中:C(T)为对训练数据的预测误差;|T|为模型的复杂度。损失函数表达两者之间的平衡。
2 典型信号波形特征分析
2.1 信号类型
依据现场人工标定,阿舍勒铜矿微震监测系统采集波形主要有电气噪音信号、爆破振动信号、机械振动信号和岩石破裂信号(图1)。电气噪音信号一般是由于微震数据传输线路靠近井下用电设备产生的,该类信号具有明显的周期性,较容易分辨;爆破振动信号是现场爆破引发的,该信号一般连续出现多次,与爆破段数呈现出较好的相关性;机械振动信号是由机械振动、凿岩等产生的振动波,波形杂乱无章,无明显的规律性;岩体破裂信号较规则,衰减规律性较好。

图1 典型信号波形Fig.1 Waveform of typical signal
2.2 信号波形特征分析
常见的波形参数主要有振铃数、持续时间、最大振幅等,如图2所示。通过Matlab软件开发的波形参数提取程序,实现微震信号波形参数提取。阿舍勒铜矿机械振动信号的振铃数较高,最小值为89,最大值为301,均值远远高于其他三种信号,但从平方差来看电气噪声信号最为稳定;机械振动信号上升振铃数也远高于其他三种信号,均值达105.82,其他三种信号的上升振铃数均小于30;在上升时间指标中,岩体破裂信号与爆破振动信号较为接近,都在0.25~30 ms范围,电气噪声信号和机械振动信号表现接近,区间主要在10~1 000 ms,平均值远高于前两者;在持续时间这一指标中,爆破振动信号与岩体破裂信号的均值接近但远小于机械振动信号和电气噪声信号的均值,岩体破裂信号的均值在50 ms左右,最大值为102.5 ms,机械振动信号和电气噪声信号的最小值均大于400 ms;爆破振动信号最大振幅的均值最大,机械振动信号与电气噪声信号的最大振幅均值接近;电气噪声信号的主频均值远小于其他三种信号。

图2 声发射信号波形参数示意图Fig.2 Waveform parameters of acoustic emission
不同波形特征参数分布小提琴图如图3所示。四种典型信号在振铃数、上升振铃数、上升时间、最大振幅、主频参数分布均有不同程度的重合,而持续时间有较大区别。电气噪音信号与机械振动信号持续时间明显大于岩体破裂信号与爆破振动信号,但岩体破裂信号与爆破振动信号持续时间无明显区别。值得注意的是,在上升时间、最大振幅等参数方面,爆破振动信号与岩体破裂信号存在一定差异。由此可见,仅依靠一种特征参数无法有效识别出岩体破裂信号。
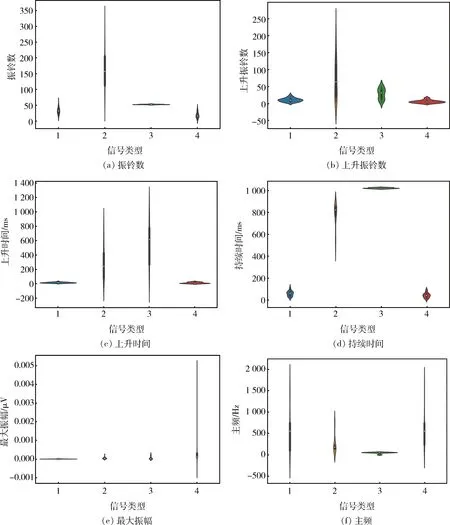
1-岩体破裂信号;2-机械振动信号;3-电气噪声信号;4-爆破震动信号
根据皮尔逊相关性计算可以得出,岩体破裂信号和爆破振动信号波形与振铃数、上升振铃数、上升时间、持续时间、最大振幅、主频六个变量之间的相关性系数分别为0.549 5、0.478 4、0.356 7、0.386 2、0.419 5、0.477 5,如图4所示。由图4可知,上升时间、持续时间与信号类型相关性相对较低,但仍然大于0.35。其他四个参数与信号类型相关性明显高于上升时间和持续时间。因此,为提高准确率,将六种波形特征参数一起输入模型识别岩体破裂信号。

图4 信号类型与波形特征参数的矩阵散点图Fig.4 Matrix scatter plot of signal type and waveform characteristic parameters
3 基于决策树分类的信号识别
从阿舍勒铜矿微震监测数据中选取248组四种典型信号数据,电气噪音信号59组,爆破振动信号55组,岩体破裂信号75组,机械振动信号59组。令岩体破裂信号为1,机械振动信号为2,电气噪声信号为3,爆破振动信号为4。其中,92组用于训练,156组用于模型测试。经过训练后的模型中,六个特征值的重要性差异较大,各特征经计算重要性得出,振铃数的权重系数为0.23,持续时间的权重系数为0.50,最大振幅的权重系数为0.27,上升振铃数、上升时间和主频的权重均为0。这说明,持续时间在识别岩体破裂信号中作用最大,其次是最大振幅和振铃数。基尼指数也称基尼不纯度,表示一个随机选中的样本在子集中被分错的可能性,其值越小,选择该属性作为分裂属性的效果越好。92组样本中,持续时间的基尼指数为0.75,小于其他属性的基尼指数,选作根节点。重复计算基尼指数,直至基尼指数为0,单个样本归类完成。此时,因为所有属性都会被考虑作为节点,模型详细且庞大,所以也造成了过拟合问题,对于训练数据外的样本识别效果并不好。为解决该问题,对模型进行剪枝处理,去掉一些节点。最终训练出的决策树模型,如图5所示。

图5 决策树识别流程图Fig.5 The identification process of decision tree algorithm
将156个检验数据输入建立的信号识别决策树模型,正确识别156个信号,错误识别2个信号,识别准确率达98.3%。其中,爆破振动信号34个,准确识别33个,准确率97.1%;岩体破裂信号46个,准确识别45个,准确率97.8%;机械振动信号和电气噪音信号个数都为38个,全部准确识别,准确率100%。
4 模型结果及对比
支持向量机(SVM)是VANIK研究团队1955年在统计学理论基础上提出的一种机器学习方法[13],较好地解决了很多学习方法的小样本、非线性、高维数、局部极小点等难点问题,具有良好的推广前景。本文通过建立SVM模型验证决策树分类算法的可靠性。模型建立时,选取高斯径向基函数(RBF函数)作为核函数。为避免SVM模型出现过拟合情况,并最大程度保证其泛化能力,该模型的惩罚参数选用0.65。在保证两种模型效果对比公平可靠的前提下,SVM建立后训练数据同样选择92组,检测数据选择156组。最终156组数据里,识别错误的组数为34组,其成功率为78.2%,其中,电气噪音信号的识别准确率为100%,爆破振动信号的识别准确率为64.7%,机械振动信号的识别准确率为100%,岩体破裂信号的识别准确率为73.9%。
决策树模型98.3%的识别准确率明显高于SVM模型78.2%的识别准确率。不同类型波形识别准确率如图6所示。从各类信号的识别准确度对比中可以看出,在识别岩体破裂信号与爆破波形信号时存在问题,这主要是因为两类波形参数分布范围较重合,识别难度较高。显然,决策树模型岩体破裂信号与爆破振动信号识别能力明显高于SVM模型。

图6 模型识别准确率对比图Fig.6 Comparison of model recognition results accuracy
5 结 论
本文采用决策树分类中的CART算法建立矿山岩体信号识别模型,得出主要结论如下所述。
1) 岩体破裂信号和爆破波形信号特征参数较相近,识别难度大,仅依靠单一的参数无法从众多类型信号中有效识别出岩体破裂信号。
2) 振铃数的权重系数为0.23,持续时间的权重系数为0.50,最大振幅的权重系数0.27,说明持续时间在识别岩体破裂信号中作用最大,其次是最大振幅和振铃数。
3) 由决策树模型检测从阿舍勒铜矿获取的波形信号,岩体破裂信号的识别准确率达到97.8%,各类信号的识别准确率均远高于常用的SVM模型,可以有效节省信号识别的人力和时间。
