尾矿库框架式排水井拱板受力模型分析研究
2022-11-22甘海阔胡贵生谢胜杰
甘海阔,胡贵生,谢胜杰
(矿冶科技集团有限公司,北京 100070)
0 引 言
排洪设施作为尾矿库安全运行的必要设施,常采用排水井、斜槽或明渠作为滩面进水构筑物,并与后续排洪构筑物相结合,构成排洪系统使用。在尾矿库常用的进水构筑物中,框架式排水井由于具有进水能力大、造价经济及运行维护方便等优势被广泛使用[1]。框架式排水井一般由下部基座(或竖井)以及上部井架部分组成,井架部分由预制钢筋混凝土拱板和现浇钢筋混凝土框架柱、圈梁组成,立柱与拱板形成的空间作为进水通道。在日常运行过程中,随着库内滩面的上升,逐步安装拱板阻挡库内不断上涨尾砂的同时,始终保持一定的泄流能力。
近年来,框架式排水井拱板破坏及整体结构垮塌事件频发,给矿山企业和当地群众生产生活以及周边环境都造成巨大的影响[2-6],通过总结分析过往排水井事故,拱板施工质量差以及拱板端部填缝质量欠佳往往是导致事故发生的重要原因。例如,2015年11月23日,甘肃陇星锑业公司崖湾尾矿库二号溢流井发生漏砂事故,经事故调查认定,拱板未按照设计要求进行安装施工导致未形成环形受压状态,排水井拱板质量未达到设计要求是拱板破损脱落形成缺口的主要原因[7]。2020年3月28日,伊春鹿鸣矿业有限公司尾矿库4#排水井同样发生垮塌事故,经事故调查认定,拱板工程质量达不到设计和施工规范要求,导致拱板先发生结构破坏并导致尾矿泄漏,最终引发排水井结构垮塌[8]。
根据《尾矿库手册》关于拱板受力模型的分析可知,框架式排水井正常运行时间,四周受环向饱和尾砂压力和水压力作用;当拱板安装在排水井立柱之间,拱板两端侧与立柱之间均留有缝隙,缝内要求用一定强度等级的水泥砂浆将此缝隙充填密实。这样拱板端侧的轴向和法向变形均受到约束,在进行拱板结构内力计算时,其受力模式可近似按双铰拱考虑[9],具体如图1所示。但在实际安装拱板过程中,当拱板端部所留缝隙内砂浆未填充密实或者用其他柔性填充物代替时(图2),拱板端部的轴向和法向变形未受到严格约束,此时按照双铰拱模型分析拱板的受力状态欠妥。当考虑一种极端工况,拱板一端轴向变形和法向变形受到约束,另外一侧的轴向变形约束完全不考虑时,拱板的受力模型可按一端铰支,一端简支的弧形简支梁考虑,具体如图3所示。
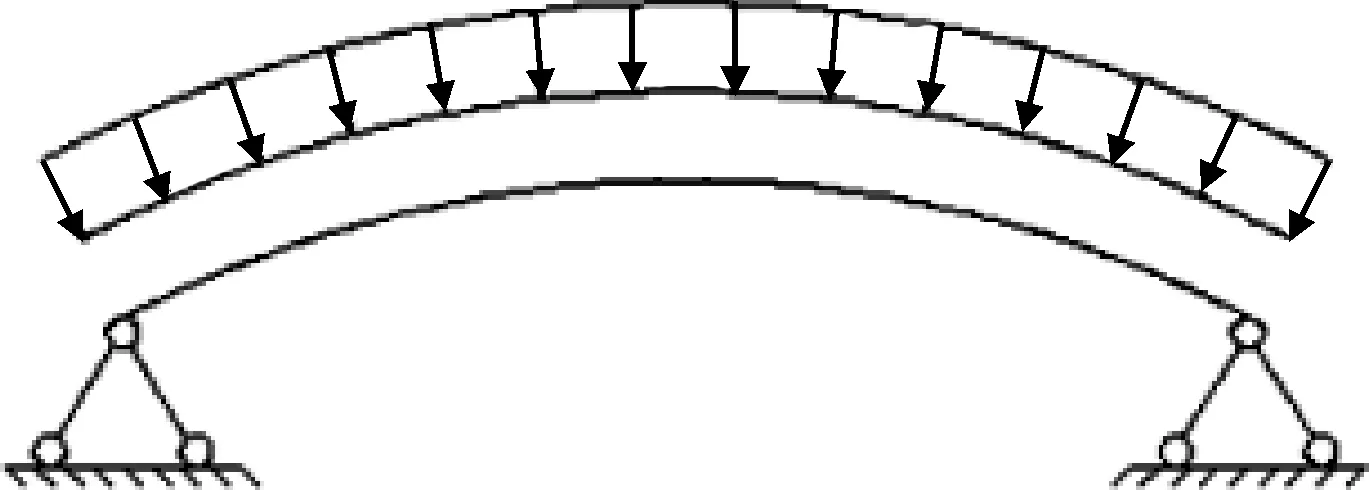
图1 双铰拱模型示意图Fig.1 Schematic diagram of double hinged arch model

图2 排水井拱板端部填缝不密实情况Fig.2 Typical case of uncompacted joint filling at the end of arch plate
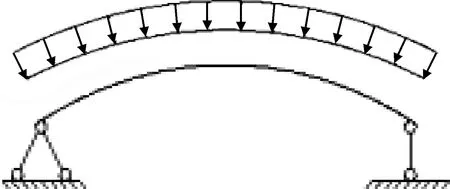
图3 简支梁模型Fig.3 Schematic diagram of simply supported beam model
本次研究以典型事故下框架式排水井为案例,以拱板端部的填缝质量问题作为分析研究工作的重点。通过构建常用的双铰拱、简支梁两种受力模型以模拟分析拱板与立柱之间的不同接触状态,对比不同模型下拱板的内力规律以及结构承载力变化情况。通过与事故发生时的拱板工作状态进行对照,以反演分析拱板破坏时的真实受力模式。结合不同填缝状态下的参数敏感性分析,分析拱板内力劣化演变规律,总结拱板结构安全控制的关键因素。研究结论可为尾矿库框架式排水井拱板在安全运行管理方面提供有力支撑。
1 典型案例分析
1.1 事故案例背景
某尾矿库框架式排水井内径为4.0 m,井高21 m,立柱共布置6根,按60°圆心角对称布置。圈梁为圆环结构,每3.0 m高度设置一层。拱板采用圆弧形构件,相关设计参数如下所述。
1) 尺寸:截面厚度×高度=100 mm×150 mm;圆弧内径2 220 mm,内弦长2 065 mm。
2) 强度及配筋形式:钢筋混凝土结构强度等级C30;拱板按照结构构造配筋配置,其中受拉侧及受压侧钢筋均配置为3根直径10 mm钢筋,拱板箍筋配置为直径10 mm钢筋,间距150 mm布置,钢筋混凝土保护层厚度15 mm。
3) 安装要求:拱板两端与立柱之间要求预留20 mm缝隙,缝隙间要求采用水泥砂浆填充密实,砂浆设计弹性模量E砂浆=1.0×104MPa。
该排水井在使用高度达到13.7 m时,底部拱板破坏漏砂,随后排水井发生倾斜后整体垮塌。事故发生后,通过对相邻封堵段的拱板开展质量检测,发现拱板存在质量问题,具体如下所述。
1) 未按设计制作拱板。实际拱板尺寸厚度×高度=150 mm×300 mm;拱板长度不足,拱板端部与框架柱之间安装缝隙略微过大,实测端部缝宽多为40~50 mm。
2) 配筋形式无法满足要求。拱板钢筋保护层厚度过大,实际保护层厚度达到17~80 mm(图4);拱板内箍筋间距达不到设计要求,设计间距150 mm,实际箍筋平均间距183 mm,个别拱板未见箍筋。

图4 排水井拱板内部钢筋配置Fig.4 Internal reinforcement configuration of drainage well arch plate
3) 安装状态不满足设计要求。拱板与立柱端部之间预留缝隙过宽,同时缝隙灌浆不饱满、不密实(图5)。

图5 拱板端部砂浆填充情况Fig.5 Mortar filling at the end of arch slab
事故调查结论表明,拱板工程质量达不到设计和施工规范要求,拱板与立柱端部之间的缝隙灌浆不饱满,导致排水井拱板承受荷载不能有效沿环向传递,改变了拱板原有的受力模型;加之拱板自身缺筋、少筋、保护层过大等质量缺陷问题,造成拱板承载能力降低,最终导致拱板破坏事故的发生。
1.2 事故时拱板状态分析
以上述典型事故案例为基础,本文以拱板端部的填缝状态为研究重点,反演分析排水井拱板破坏时的真实受力状态。在进行结构安全反演分析时,拱板参数选取如下所述。事故时排水井附近地质资料见表1。

表1 排水井附近各地层物理力学指标Table 1 Physical and mechanical indexes of each formation near the drainage well
1) 尺寸形式。拱板内弦长取实际平均值2 060 mm,圆弧内径取2 220 mm,拱板厚度×高度=150 mm×300 mm。
2) 配筋形式。受拉侧钢筋混凝土保护层厚度按照质量检测结果平均值60 mm考虑,箍筋布置间距取检测统计后的平均值283 mm。
3) 安装状态。为模拟分析拱板端部的不同填缝接触状态,采用双铰拱模型模拟设计填缝状态,采用简支梁模型模拟拱板一端未填缝时的接触状态。
底部单块拱板所承受的饱和水和尾砂压力荷载计算见式(1)。
q=h×qmax=h×[γ水×H+
(γf1×H1+γf2×H2+γf3×H3)×Ka]
(1)
式中:h为单块拱板的截面高度;qmax为最下层拱板所承受的环向均布力作用,kN/m2;γ水为水的容重;γf1为底层粉质黏土层尾砂浮容重;γf2为淤泥质粉质黏土层浮容重;γf3为浮泥尾砂浮容重;H为排水井上覆尾砂+水的总高度;H1为粉质黏土层尾砂层厚度;H2为淤泥质粉质黏土层尾砂层厚度;H3为浮泥尾砂层厚度;H4为清水层层厚度;Ka为主动土压力系数。
经计算,排水井最底部单块拱板高度(拱板高度300 mm)所承受的外部均布荷载为q=59.69 kN/m。
1.3 不同模型下内力对比分析
采用结构力学分析方法计算两种受力模型下的拱板内力,计算结果如图6和图7所示。 由图6和图7可知,双铰拱模型下拱板轴力为129.163 kN,拱端最大剪力为3.225 kN,跨中最大弯矩为1.756 kN·m。该模型下拱板所承受的外部荷载大部分转化为轴向作用力,拱板内力中弯矩较小,端部剪力小。简支梁模型下拱板的轴力为27.897 kN,拱端最大剪力为54.787 kN,跨中最大弯矩为29.840 kN·m。该模型下拱板所承受的外部荷载大部分转化为剪力以及弯矩,拱板弧形梁内轴力较小。双铰拱模型下,拱板内力中的剪力和弯矩均较小,拱板近似处于受压状态,此时受力条件较好。当处于简支梁模型状态,受力条件变差。

图6 双铰拱模型下拱板内力结果Fig.6 Internal force results of arch plate under the double hinged arch model
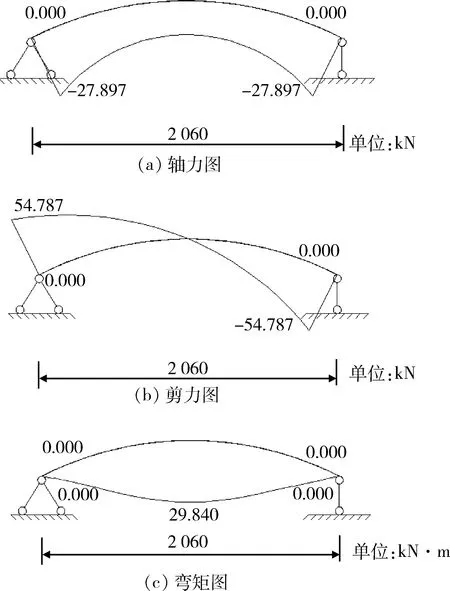
图7 简支梁模型下拱板内力结果Fig.7 Internal force results of arch plate under simply supported beam model
1.4 承载能力对比分析
通过上述分析,在饱和水和尾砂荷载作用下,拱板同时弯矩和轴力,实际上为偏心受压构建。本次基于矩形截面偏心受压构建受压承载力分析方法对拱板结构进行正截面安全分析(图8)[10],表达式见式(2)~式(4)。
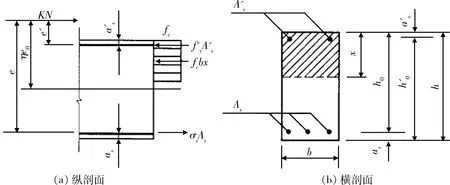
图8 矩形截面偏心受压构建受压承载力分析方法Fig.8 Schematic diagram of bearing capacity analysis of eccentric compression structure with rectangular section
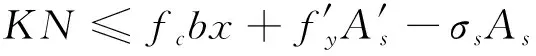
(2)
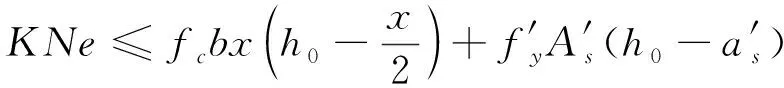
(3)
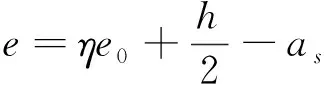
(4)

不同受力模型下拱板承载力分析结果见表2。通过与拱板实际截面配筋面积对比可知,双铰拱模型下拱板结构承载力极高,在该受力模式下,未配置钢筋下的素混凝土拱板可承受21 m设计高度下饱和水和尾砂作用。简支梁模型下拱板结构承载力极低,现有拱板无法抵抗1.0 m高度下的饱和水和尾砂压力荷载作用。 排水井在使用至13.7 m高度时底部拱板发生破坏。因此,拱板破坏时的实际受力状态应介于双铰拱与简支梁模型之间。

表2 不同受力模型下拱板承载力分析结果Table 2 Bearing capacity results of arch slab under different stress models
2 拱板实际受力模型分析
2.1 端部实际接触状态
对比事故案例的排水井,拱板与立柱端部之间存在砂浆填缝厚度过大、填缝不密实、填缝质量差的情况。此时,拱板两端的轴向变形受到一定约束,但约束条件未完全达到双铰拱不会变形的刚度。同时又未达到简支梁一侧轴向变形完全不受约束的程度。按照上述分析,拱板可视为两端分别为竖向连杆+轴向弹簧的受力状态(图9),轴向弹簧的刚度系数取决于拱板端部与立柱的接触状态。拱板拱端的内力最终传递到拱端砂浆以及相邻的立柱上,正常情况下立柱中心截面可视为不动,当以两侧立柱截面中心点作为定点,填充之内的砂浆以及立柱一半的截面视为弹簧支座,弹簧支座的综合刚度系数K综合则取决于砂浆的刚度以及立柱混凝土截面的刚度,表达式见式(5)~式(7)。
图9 弹簧拱模型示意图Fig.9 Schematic diagram of spring arch model
K综合=K砂浆×K立柱/(K砂浆+K立柱)
(5)
K砂浆=E砂浆×A截面/L砂浆
(6)
K立柱=E立柱×A截面/L立柱
(7)
式中:K综合为支座综合刚度系数;K砂浆为砂浆部分刚度系数;K立柱为砂浆部分刚度系数;E砂浆为砂浆弹性模量;E立柱为立柱混凝土弹性模量;A截面为填缝满浆状态下截面面积;L砂浆为填缝砂浆厚度;L立柱为立柱厚度,取立柱截面的一半。
一般情况下,立柱的刚度K立柱可视为保持不变。砂浆的刚度则受拱板端部填缝施工因素影响波动较大,该值取决于即取决于填缝厚度、填充砂浆面积、砂浆弹性模量等因素。当填缝厚度L砂浆变大,将导致刚度系数降低;砂浆未充填密实密,导致接触面积A截面降低,并导致刚度系数降低;砂浆填缝不均匀、不密实,将降低砂浆部分的等效弹性模量E砂浆。上述情况最终也将导致砂浆整体刚度系数降低,拱板端部砂浆填缝质量对端部接触时的刚度系数影响较大。
2.2 弹簧拱模型下内力变化规律
本文采用有限元分析软件建立拱板内力分析的弹簧拱模型,针对不同支座刚度系数对内力的影响开展参数敏感性分析,计算结果如图10~图12所示。
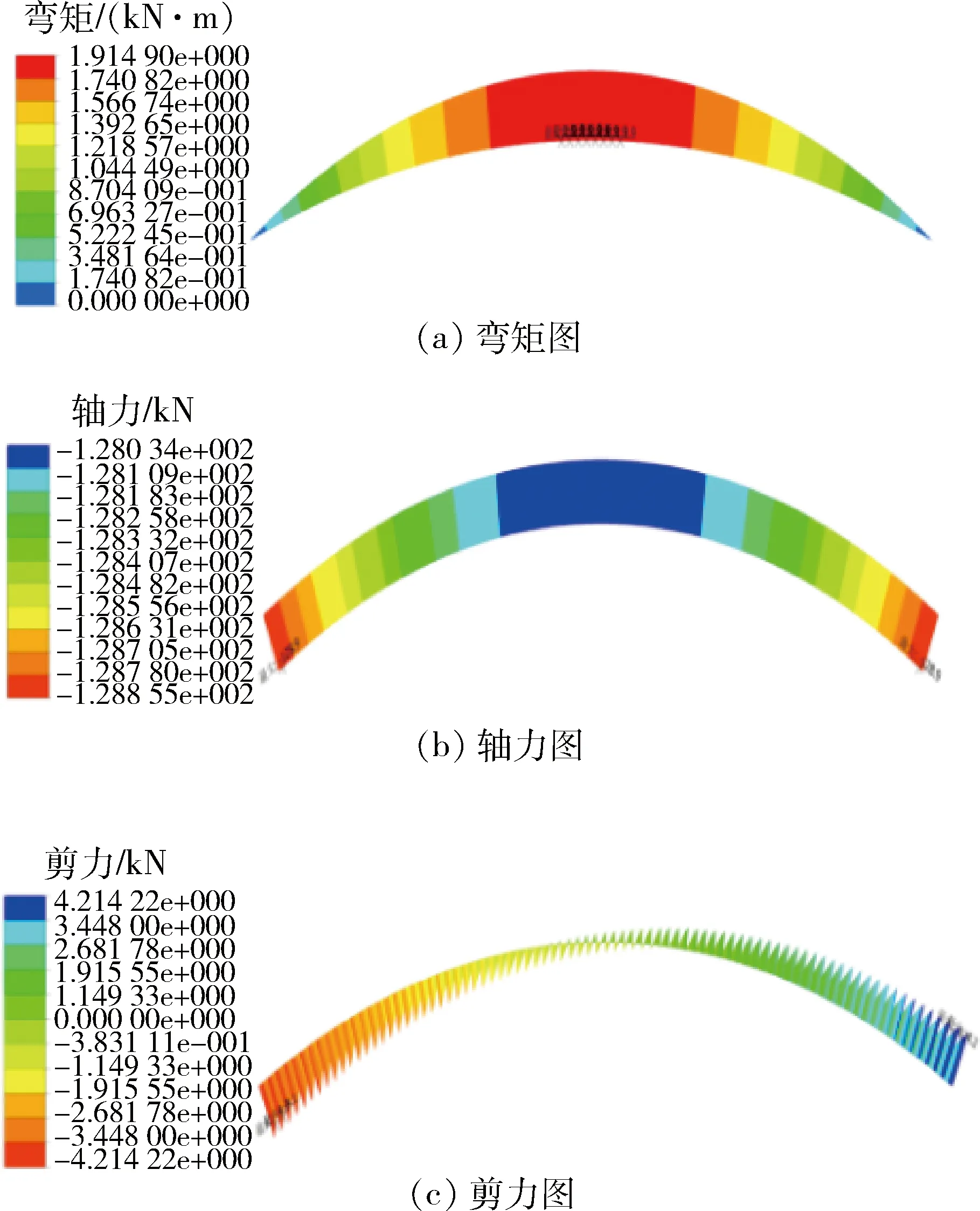
图10 设计工况下拱板内力Fig.10 Internal force of arch plate under design condition

图11 刚度系数降低至K综合=70万kN/m时拱板内力Fig.11 Internal force of arch plate when the stiffness coefficient is reduced to K综合=70万kN/m
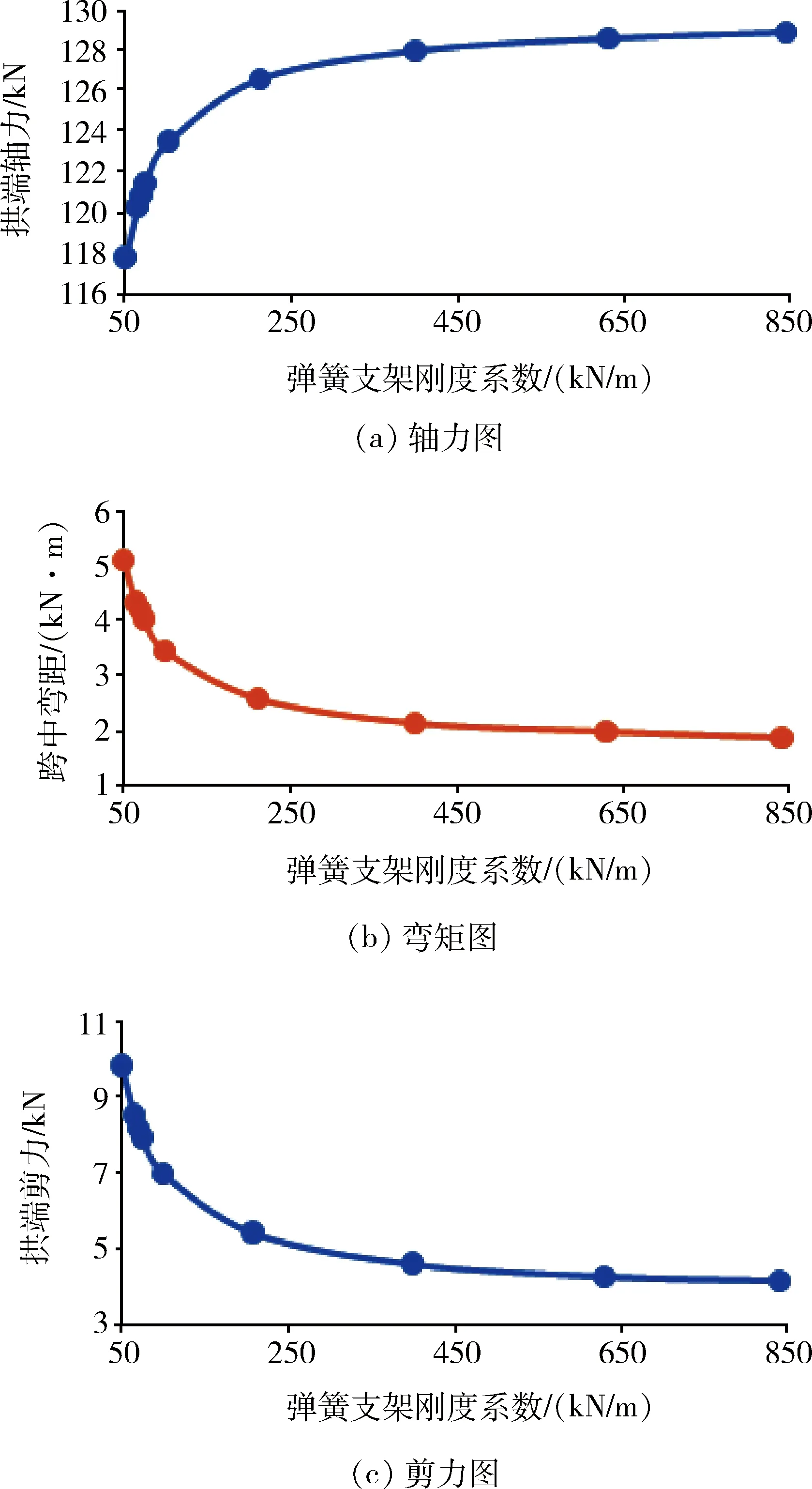
图12 不同弹簧支座刚度系数下拱板内力变化规律Fig.12 Variation law of arch plate internal force under different spring support stiffness coefficients
1) 图10为设计工况下拱板内力计算结果。当按照设计填缝密实状态进行拱板内力计算时(设计填缝宽度20 mm,砂浆满浆状态,砂浆弹性模量取设计弹性模量E砂浆=1.0×104MPa),经计算端部综合刚度系数Kmax=843.75万kN/m,该工况下计算拱板轴力为128.9 kN,拱端剪力4.20 kN,跨中弯矩1.91 kN·m。由图10可知,端部满浆状态下弹簧拱下内力结果与双铰拱模型下结果基本一致。
2) 图11为当K综合达到双铰拱模型内力计算结果的8.3%(K综合=70万kN/m),此时拱板轴力为121.0 kN,端部剪力为8.2 kN,跨中弯矩4.2 kN·m。相比设计工况而言,拱板的拱端轴力有所减小,拱端剪力和跨中弯矩则有所增加。
3) 图12为不同弹簧刚度系数下拱板内力变化规律。由图12可知,在一定的弹簧刚度区间内,弹簧拱模型下内力与双铰拱模型下内力接近。但随着弹簧刚度系数降低,拱端轴力逐步减小,拱端剪力和跨中弯矩则呈逐步增加,表现为两种受力模型下结果差异逐步增大。
4) 当一侧弹簧刚度系数趋近于0时,弹簧拱与简支梁模型下内力计算结果基本一致。
2.3 弹簧拱模型下承载力变化规律
对不同弹簧支座刚度系数下拱板承载力进行分析,重点分析弹簧刚度系数不断降低情况下拱板的承载力变化规律,计算结果如图13所示。以设计工况下端部刚度系数Kmax=843.75万kN/m作为参照,经分析可得:①当K综合∈(0.2Kmax,Kmax)时,该阶段素混凝土拱板可满足相应荷载下结构承载力要求;②当K综合∈(0.075Kmax,0.2Kmax)时,拱板受拉侧需要配置钢筋截面面积,但该阶段尚未超过拱板承载能力;③当K综合=0.075、Kmax=65万kN/m时,拱板受拉侧需要配置钢筋截面面积大于实际配筋截面235.5 mm2,对应于此时拱板发生破坏;④当K综合<0.075Kmax时,拱板受拉侧需要配置钢筋截面面积将显著增大;⑤拱板弹簧支座端部刚度系数的降低,将显著劣化拱板的承载能力。
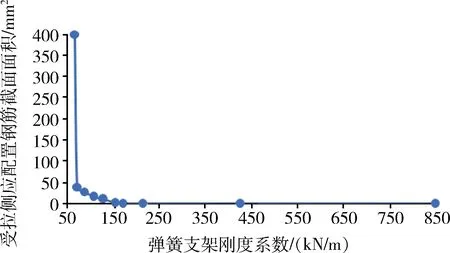
图13 不同弹簧支座刚度系数下拱板承载力变化规律Fig.13 Variation law of arch plate bearing capacity under different spring bearing stiffness coefficients
3 结 论
本文以典型事故案例下排水井为例,在深入分析端部填缝质量的基础上,分别构建双铰拱、简支梁以及弹簧拱等多种受力模型,以模拟拱板端部的几种不同接触状态,反演分析排水井拱板破坏时的真实受力状态,得出结论如下所述。
1) 拱板与立柱之间的接触状态决定了拱板的受力状态。当拱板端部填缝质量较好时,拱板实际受力模式为端部刚度系数较高的弹簧拱模型,接近于理论上的双铰拱模型;当拱板端部未用砂浆填缝密实时,拱板的实际受力模式将发生改变,由双铰拱模型转化为刚度较低的弹簧拱甚至简支梁模型。
2) 为提高框架式排水井安全度,拱板结构配筋设计宜按照简支梁或刚度极低的弹簧拱模型考虑。当按照弹簧拱模型进行拱板偏心受压结构安全分析时,应充分考虑端部填缝质量差所造成的弯矩及剪力增加、轴力减小等不利因素。
3) 企业日常运行管理过程中,应对预安装的拱板进行质量检测,确保拱板施工质量、各项尺寸等符合设计要求,并保证端部砂浆填缝密实状态,以确保拱板封堵后排水井的结构安全。
