基于改进TOPSIS方法的烤烟化学品质综合评价

张勇刚，任志广，张晓兵，项波卡，程昌合

浙江中烟工业有限责任公司技术中心，杭州市西湖区科海路118号 310024

烟叶的主要化学成分是烟叶品质鉴定的重要指标，是确定烟叶品质和风格特征的物质基础，烟叶化学成分的质量分数和比例直接影响烟叶的品质［1］。不同烟叶化学成分指标可以从不同侧面反映烟叶的品质状况，但单个指标很难完整表征烟叶化学成分状况［2］。借助多指标综合评价方法将多个化学成分指标综合成一个单指标的形式，进而开展烟叶化学成分的综合评价与分析，对于探究不同生态区域、品种的化学品质差异［3-7］以及化学品质对农艺措施的响应［8］等具有重要作用。

Hwang等［9］于1981年 提 出的 逼 近 理 想解 法（Technique for order preference by similarity to an ideal solution，TOPSIS）是系统工程中对有限方案进行多目标决策分析的决策技术，其基本原理是先对原始数据矩阵进行标准化，构造得出评价方案中的正、负理想解，然后分别计算每个评价对象与正、负理想解的加权欧氏距离，从而得出该方案与理想解的贴近程度，根据相对贴近度的大小对评价结果排序［10-11］。李富欣等［12］、黄瑞寅等［13］采用TOPSIS法开展了烟叶质量综合评价，卢秀萍［14］、李彦平等［15］采用TOPSIS法对烤烟区域试验中各品种的多性状进行综合评判。另外，TOPSIS法也常用于湖泊水质评价［16］、电能质量评价［17］、土壤质量评价［18］等领域，并取得了较好效果。相关研究表明，TOPSIS法能够充分利用原始数据，计算过程数据丢失量较小，几何意义直观［19］。但其自身也存在一定不足，如对于位于正理想解和负理想解连线中垂线上的点，相对贴近度恒为0.5［20］，会出现无法评价的情况；增加或减少评价对象时，如果影响到理想解的改变，那么原有评价对象的优劣排序可能发生变化，导致决策难产或决策混乱［21］。因此，本研究中在已有文献的基础上，通过确定评价对象的绝对理想解、改变评价指标标准化值的取值范围、优化权重的加权时机，提出一种改进的TOPSIS方法，并将其应用于烟叶的化学品质评价，以期为烟叶质量评价方法的完善提供参考和借鉴。

1 材料与方法

1.1 材料与检测指标

所有烟叶样本均取自四川省主要植烟市（州）（凉山州、宜宾、泸州、攀枝花、广元），品种为云烟87，等级为B2F，取样时间为2020年，共计45个样本，测定与计算的指标包括烟碱、总糖、还原糖、氯、钾、总氮、氮碱比和糖碱比，测定方法参考文献［22］进行；采用企业原烟感官质量评价方法，由7位获得国家烟草质量监督检验中心颁发的感官评吸证书的评价人员对香气质、香气量、杂气、余味、刺激性、柔和度、细腻度、圆润感和干燥感等指标进行定量打分，单项满分分别为25、20、15、10、10、5、5、5和5分，合计100分，以评价小组打分的平均值作为各项感官质量指标的最终分值［23-24］。

1.2 方法

1.2.1 改进TOPSIS方法

1.2.1.1 传统TOPSIS方法的缺陷

（1）自相矛盾问题：当两点位于正理想解、负理想解连接线的某根垂线上时，如果该垂线在正、负理想解连线的中垂线左侧下方，则评价结果和垂线位于中垂线右侧上方自相矛盾［25］，如图1所示。

（2）中垂线问题：对于位于正理想解和负理想解连线中垂线上的点，无法区分优劣，相对贴近度恒为0.5［26］。

为进一步说明上述两点不足，以图1为例，W、B分别为负理想解和正理想解，J、K为处于WB连线中垂线右上方的两个评价对象，C、D为处于WB连线中垂线左下方的两个评价对象，M、N为处于WB连线中垂线上的两个评价对象；JL⊥WB，WL=e，LB=f，JK=g，KL=h；相对贴近度用T表示。

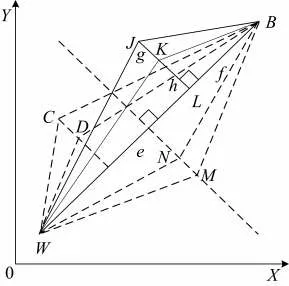
图1 传统TOPSIS法中的自相矛盾和中垂线问题Fig.1 Issues of self-contradiction and mid-perpendicularity in traditional TOPSIS method

以J、K为例：

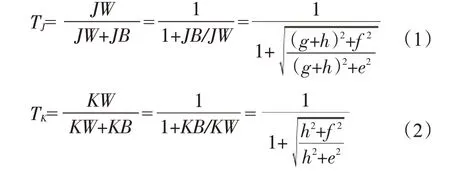
TJ与TK的大小取决于两者根号下数值的大小：

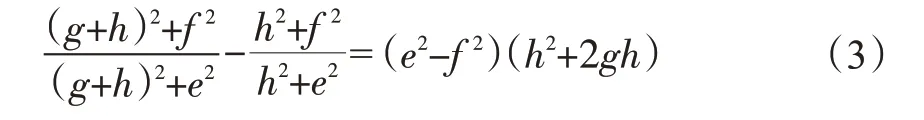
由图1可知，当e＞f时，TJ＜TK；当e＜f时，TJ＞TK；当e=f时，TJ=TK=0.5。

对于上述3对评价对象，按照传统TOPSIS方法的基本步骤计算可得：TJ＜TK、TC＞TD、TM=TN=0.5，显然这样的结果不合理。因为在C、D和J、K这两对样本点中，D和K具有相同的地位（距离WB连线近且距离最优点B近），C和J具有相同的地位（距离WB连线远且距离最优点B远），故两对样本点各自排序应为D优于C、K优于J或D劣于C、K劣于J。事实上，D与C相比距最优点更近，且距WB连线更近，理应有D优于C，同理应有K优于J［25］。即TC＜TD，TN＞TM。

（3）逆序问题：当增加或减少某些评价对象时，会引起其他评价对象排序的颠倒［27］。逆序问题将使原来所做的评价工作均变得毫无意义［28］。逆序问题产生的根本原因是评价标准发生了变化［29］。

1.2.1.2 改进TOPSIS方法的建立

（1）数据标准化：化学成分指标的标准化一般采用隶属度函数进行，根据已有文献及产区实际［3，30-31］，确定隶属度函数类型及转折点值见表1。

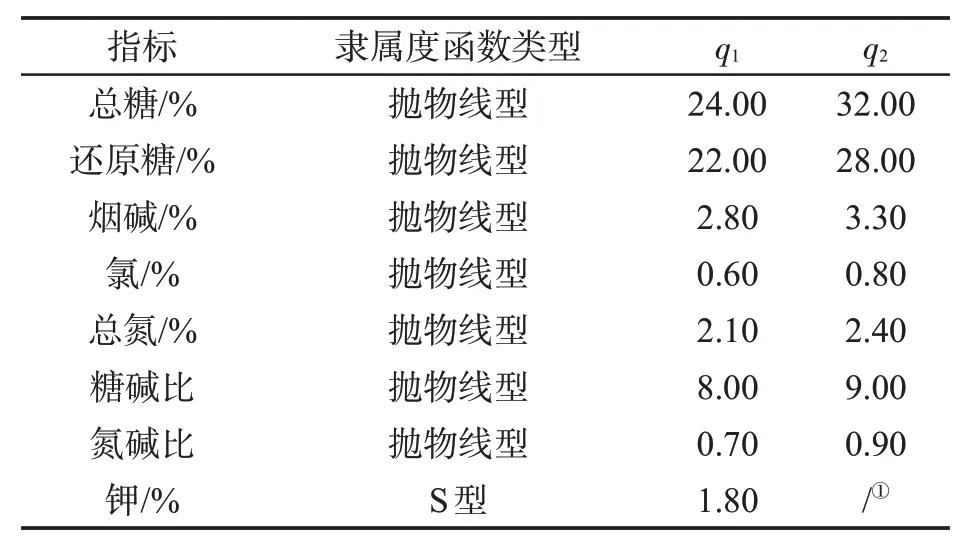
表1 化学成分指标的隶属度函数及拐点值Tab.1 Membership function types and inflection points of chemical component indexes

对于S型指标：

对于抛物线型指标：

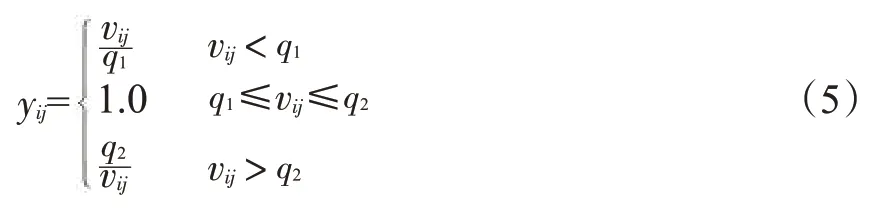
式中：vij为第i个烟叶样本的第j个化学成分指标的实测值，yij为第i个烟叶样本的第j个化学成分指标的一次标准化值，q1、q2为隶属度函数的转折点。

鉴于评价对象处于中垂线右上方时，能够获得较为合理的结论。本研究中对原始数据的标准化矩阵Y进行二次标准化，取正理想解的1/2进行线性转换，使最大值为1，最小值为0.5［公式（6）］，实现所有数据约束在正、负理想解连线垂线的右上方正方形内（图2），这样自相矛盾及中垂线的问题就能得到解决。

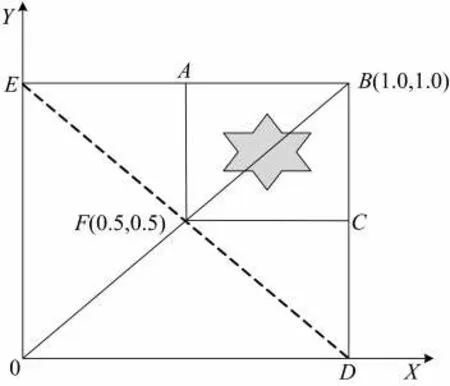
图2 初始标准化矩阵的改进Fig.2 Improvement of original data standardized matrix

式中：xij为第i个烟叶样本的第j个化学成分指标的二次标准化值，则原始数据的标准化矩阵转化为X=［xij］mn。

（2）确定正、负理想解：由标准化公式的特点，绝对正理想解可设置为1，为防止评价过程中再次出现自相矛盾和中垂线问题，将绝对负理想解设置为0，实现理想解不随评价对象的增减而变动。

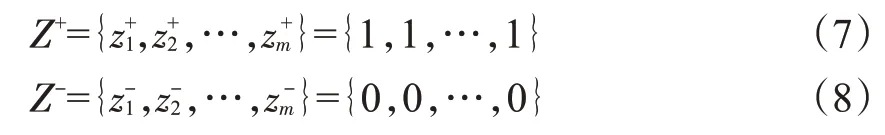
（3）权重确定：采用基于几何平均复合判断矩阵的层次分析法［32］确定化学成分指标权重，防止评价对象增减时因采用主成分分析法等客观赋权法导致的权重值发生变化。

假设有l个专家依据层次分析法的1～9标度对化学成分重要性进行两两比较，并赋值得到l个判断矩阵A（l）=（aij）nn=（aij=1/aji；l=1，2，…，k），采用方根法计算判断矩阵的最大特征值λmax、特征向量和一致性比例CR（Consistency ratio），并进行一致性检验。当一致性比例CR＜0.1时，判断矩阵一致性检验通过，即认为该判断矩阵具有满意的一致性，所得权重有效，否则对判断矩阵进行调整。

为进一步综合多个专家的意见，本研究中针对不同判断矩阵的对应元素求取几何平均值，构造得出复合判断矩阵。已有研究［33-34］表明，在采用层次分析法进行群决策时，若k个专家给出的所有判断矩阵具有满意一致性，则几何平均复合判断矩阵也具有满意的一致性，综合群体意见的同时不必再进行一致性检验。对于具有满意一致性的k个判断矩阵A（l），几何平均复合判断矩阵为：

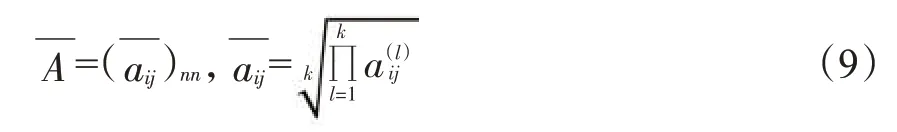
（4）计算距离：传统的TOPSIS法计算距离时，平方后权重之和不再等于1，权重的影响被放大，从而扩大了权重对决策结果的影响［35］。因此，本研究中将先加权后计算欧氏距离改为求取欧氏距离同时加权，保证不改变标准化数据间的关系结构，符合权重使用的原意［27］。

每个烟叶样本到正理想解的距离Si+和到负理想解的距离Si-，可改写为：

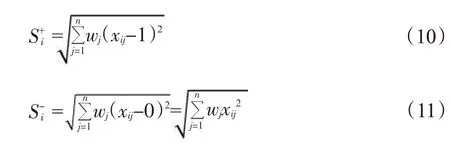
（5）计算每个烟叶样本与理想解的贴近度：

Ti∈［0，1］，Ti越大，表示烤烟化学品质越优。

由上述步骤可知，在实际评价时，增加或者减少评价对象，对已有评价对象的标准化值无影响，权重值、理想解均不会发生变化，改进TOPSIS方法评价结果具有抗逆序性［36-37］。

2 结果与分析

2.1 化学成分的标准化

45个烟叶样本不同化学成分指标的描述性统计结果见表2。结合表1，烟叶样品间化学指标整体表现为总糖的质量分数偏高、氮碱比适中偏低、氯的质量分数偏低；另外，氯的质量分数分布于适宜区间（q1～q2）的比例最小，仅为2.22%，其变异程度明显高于其他指标，达56.56%；还原糖的质量分数分布于适宜区间的比例最大，为82.22%，在样品间变异程度相对较小，为9.25%。

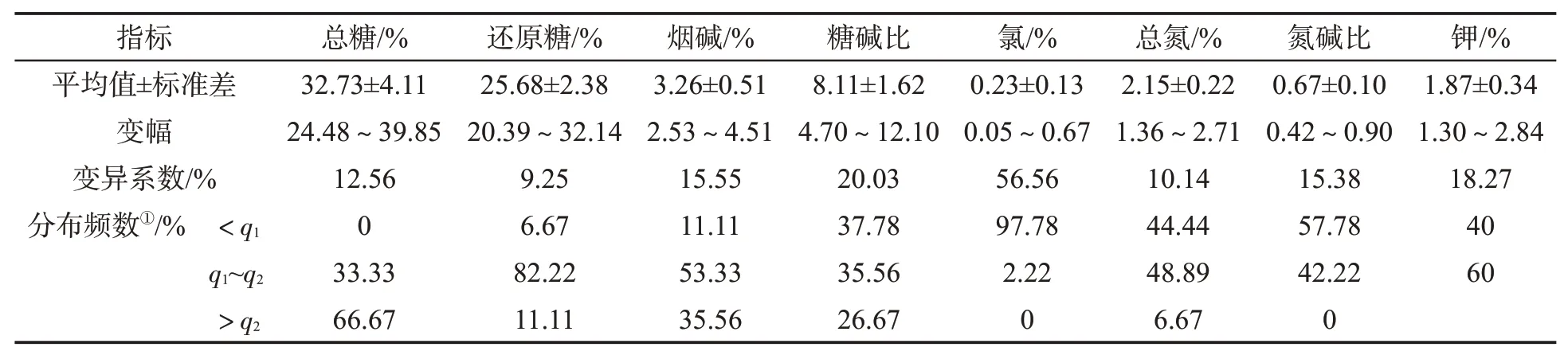
表2 化学成分指标的描述性统计Tab.2 Descriptive statistics of chemical component indexes

依据公式（4）、公式（5）和公式（6）分别对不同化学成分指标进行一次标准化和二次标准化，其基本描述统计结果分别见表3和表4。

表3 化学成分指标的一次标准化值Tab.3 Primary standardized values of chemical component indexes

由表4可知，经二次标准化后，不同化学成分指标的变异系数均变小，缩小了数据之间的差异，但由于采用的是线性转换，不会改变同一化学成分不同烟叶样本标准化值的优劣排序。

表4 化学成分指标的二次标准化值Tab.4 Secondary standardized values of chemical component indexes

2.2 化学成分指标权重计算

由5名获得国家烟草质量监督检验中心颁发的感官评吸证书的人员依据1.2.1.2节中的方法对化学成分指标进行赋权，结果见表5。可知，依据1～9标度得出的判断矩阵CR值均小于0.1，具有满意的一致性，可以构建几何平均复合判断矩阵，进而求取化学成分指标的复合权重。

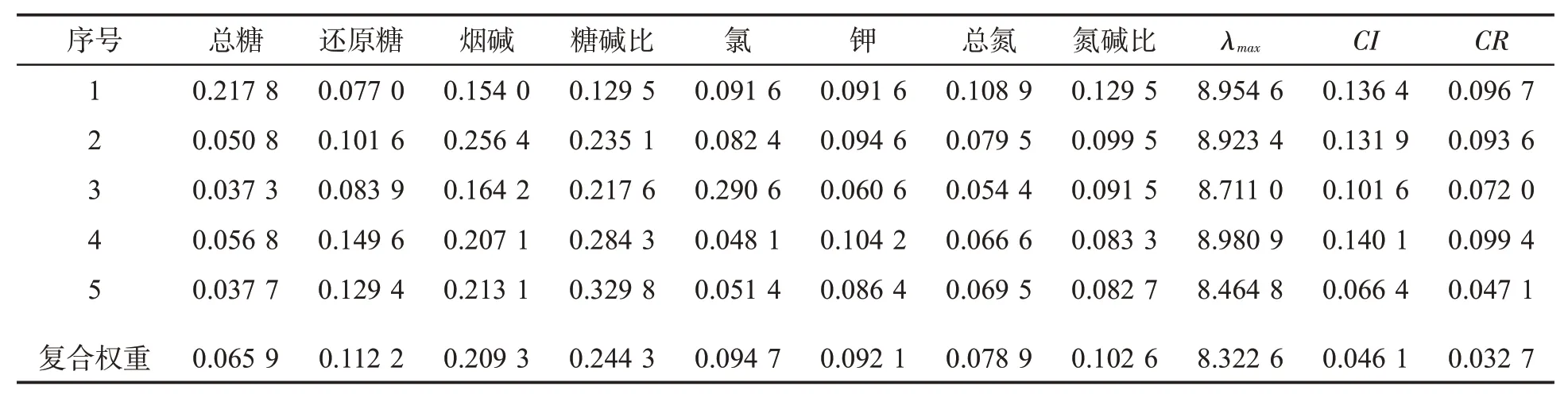
表5 化学成分指标的权重Tab.5 Weights of chemical component indexes

采用Spearman等级相关系数考察复合权重与每位专家赋权结果的一致性，复合权重与专家1～专家5权重的相关系数分别为-0.048 2（P＞0.05）、0.952 3（P＜0.01）、0.738 1（P＜0.05）、0.809 5（P＜0.05）和0.881 0（P＜0.01），说明基于几何平均复合判断矩阵的层次分析法能够综合绝大多数专家的意见，避免个别专家主观意见的影响。

2.3 化学品质综合评价

由改进TOPSIS法计算得出的45个烟叶样本的相对贴近度见表6。

为说明本方法的改进效果，分别计算传统TOPSIS法、改进TOPSIS法的相对贴近度与感官质量指标的Pearson相关系数和Spearman等级相关系数，结果如表7所示。可知，改进TOPSIS法相对贴近度与感官质量指标的Pearson相关系数和Spearman等级相关系数的平均值分别为0.214 8和0.189 3，均高于传统TOPSIS法的0.177 8和0.155 7。改进TOPSIS法相对贴近度与杂气的Pearson相关系数为0.360，与柔和性的Pearson相关系数为0.312，与杂气的Spearman等级相关系数为0.311，均达到显著水平；传统TOPSIS法相对贴近度仅与杂气达显著水平。说明改进TOPSIS法与感官质量较传统TOPSIS法更为密切，所得评价结果基本可行，具有一定的可靠性。

表7 TOPSIS相对贴近度与感官质量指标的相关性分析①Tab.7 Correlation analysis between TOPSIS relative closeness degree and sensory quality indexes

基于改进TOPSIS法的相对贴近度，采用平方欧氏距离-Ward系统聚类法将45个样本划分为3类：第一类包含6个样本，T均值为0.942 6，为化学品质较好的样本；第二类包含16个样本，T均值为0.908 5，为化学品质中等的样本；第三类包含23个样本，T均值为0.874 9，为化学品质较差的样本。不同类别烟叶样本的相对贴近度对应的感官质量得分见表8，可知，相对贴近度越高，烟叶样品的大部分感官质量指标的平均分值也越高，进一步验证了改进TOPSIS法所得评价结果总体上是可行的。

表8 不同类别烟叶样本的相对贴近度及感官质量得分Tab.8 Relative closeness degrees and sensory quality scores of different type tobacco samples

3 结论

①二次标准化法使得评价对象均处于正、负理想解中垂线的右上方，克服了相对贴近度可能无法真实表征评价对象优劣的缺陷；②通过设置绝对理想解、采用主观赋权法赋权和改变加权时机，保证了评价对象的增减不会改变正、负理想解，进而可以实现评价结果的抗逆序；③通过实例计算及其与感官质量的比较分析，表明改进TOPSIS方法在烤烟化学品质评价中的应用是有效的，其评价结果具有一定合理性。