Properties of Titanium isotopes in complex momentum representation within relativistic mean-field theory
2022-11-21TaiHuaHengYaoWuChu
Tai-Hua Heng• Yao-Wu Chu
Abstract The self-consistent quadruple potential is deduced within the relativistic mean-field (RMF) framework and substituted into the Hamiltonian, which is calculated using the complex momentum representation(CMR). Considering even-even titanium isotopes as an example, this study investigated various properties,including the resonant states of neutron-rich nuclei in the RMF-CMR model, and used them to describe the binding energy. The abrupt decrease in the two-neutron separation energy (S2n) corresponds to the traditional magic number.The resonant and bound states are simultaneously exposed in the complex moment plane, where the continuum is along the integration contour. The four oblate neutron-rich nuclei 72-78Ti are weakly bound or resonant because their Fermi energies are approximately 0 MeV. The root-meansquare (RMS) radii of these nuclei increase suddenly compared with those of others (neutron number N<48).Moreover, 78Ti and 76Ti are determined as drip-line nucleons by the value of S2n and the energy levels,respectively. Finally, the weak-bounded character can be represented by diffuse density probability distributions.
Keywords Resonant states ∙Self-consistent potential ∙Complex momentum representation
1 Introduction
In past decades, the location of the edge of the nuclear chart has become an important issue in nuclear physics.As is well known, the neutron-side drip line can be experimentally determined from oxygen isotopes up to Z =10[1, 2]. Generally, nuclei that are far from the β stable line exhibit interesting properties,such as deformation structure[3], new magic number [4], halo [5, 6], giant halo phenomena [7], and β decay[8], owing to the large N/Z ratio.The halo of11Li and deformed halo of31Ne can be explained by simultaneously considering the continuum and resonant states. Therefore, the theory of nuclear structure is not only appropriate for investigating the bound states but also for investigating the resonant states and continuum states.
In recent years, relativistic mean-field theory has become established[9]because it successfully explains the β+/EC decay [10], charge-exchange excitations [11], shell correction energies[12],nuclear mass precision[13],shape phase transitions[14,15]of spherical and deformed nuclei,hypernuclei [16, 17], nuclear matter [18, 19], and descriptions of astrophysical r-process simulations[20, 21]. To date, several methods have been developed to study the properties of resonant states. Some of these methods, such as the R-matrix [22], K-matrix [23], and Smatrix [24, 25], are based on scattering theory. However,resonant states are dealt within a manner similar to bound states. For example, by the analytic continuation in the coupling constant (ACCC) [26] method, resonance states become bound states, and the physical quantities can be obtained from the bound-state solutions through the Pade´approximate (PA) order. Several neutron-rich nuclei have been investigated using the ACCC method combined with relativistic mean-field(RMF)theory[27,28].The equation of motion in the real stabilization method (RSM) [29] can be solved based on a box of finite sizes, and the energy is stable against changes in the size of the basis or box.However, this method is not suitable for broad-width resonant states. Satisfactory results for spherical nuclei120Sn have been obtained by using Green’s function (GF) to solve the density of states in coordinate space[30,31].The complex scaling method(CSM)[32]is used in atomic and molecular physics and nuclear physics [33, 34]. Based on the RMF-CSM method, the resonant states of spherical[35, 36] and deformed nuclei have been analyzed [37].
Although RMF-RSM, RMF-ACCC, and RMF-CSM are effective tools for dealing with resonant states, various limitations still exist, and it is difficult to obtain the resonance state near the threshold of the continuum spectrum with satisfactory accuracy. Additionally, the result calculated using the CSM method is affected by the rotation angle.Recently,because the bound and resonant states can be shown simultaneously by solving the equation of motion in complex momentum space, a scheme wherein the complex momentum representation (CMR) is applied to the RMF framework was established[38].Using the RMFCMR method,several quantities of the resonance states can be obtained for the spherical system[39,40].Additionally,the deformed nuclei characteristics have been investigated using a Woods-Saxon type potential for both nonrelativistic [41, 42] and relativistic cases [43] in a complex momentum plane. Numerous novel conclusions have been drawn for typical halo nuclei such as37Mg,31Ne,and19C.This study considered titanium isotopes as an example and investigated various properties using the RMF-CMR method within the self-consistent potential obtained by iteratively solving the Dirac equation in the RMF framework. The rest of this paper is organized as follows. Section 2 presents the derivation of the theoretical formulas.The numerical details and results are presented in Sect. 3.Finally, the summary and direction of future work are presented in Sect. 4.
2 Theoretical framework
To deduce the self-consistent potential as the starting point, the following Lagrangian of RMF theory is given:

where M denotes the nuclear mass; mσ(gσ), mω(gω), and mρ(gρ) represent the masses (coupling constants) of the respective mesons; g2, g3, c3, and d3are self-coupling coefficients.
The corresponding Dirac equation in cylindrical coordinates is used to investigate the characteristics of the deformed nuclei and is expressed as follows:
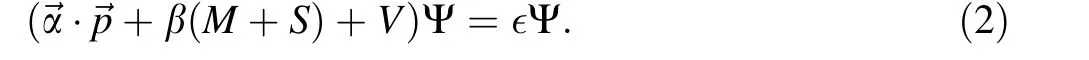
where α→and β are Dirac matrices; S and V are the scalar and vector potential, respectively. The solution of this equation includes the bound states and continuum with the following complete condition:

where Ψband Ψcare the wave functions of the bound states and continuum, respectively.
Several methods, such as the shooting method [44] and finite element method [45], have been developed to solve the Dirac equation. Notably, spurious states can be completely avoided because the Dirac equation is considered within momentum space.To investigate the resonant states submerged in the continuum, the Dirac equation must be converted into the following complex momentum plane:Here, χmsis the spin wave function with the third component of the spin angular momentum ms, and Ylm(Ωk)denotes the spherical harmonics in complex momentum space.

By substituting Eq. (5) into Eq. (4), the Dirac equation becomes as follows:

At this point, the Dirac equation can be treated by solving the eigenvalue of a symmetric matrix in Eq. (9). More details regarding this formulation can be found in the literature [41, 43].
3 Numerical details and results

Fig. 1 (Color online) Binding energies as function of mass number.The blue diamonds represent the data in AME2020.The black squares represent the values calculated using RMF-CMR model
Based on the above-mentioned theoretical formula,various properties of Ti isotopes, such as the binding energy, single-particle energy level, S2n, RMS radius, and probability distribution, can be investigated. To study the characteristics of resonant states,the neutron number of the Ti isotopes is considered to be up to 56 (78Ti). In this calculation, the coupled-channel model is adopted and the PK1 parameter group is selected. The number of coupling channels (nch) is equal to four. The infinite complex momentum plane is truncated at Re k=4.0 fm-1,which is sufficient for the convergence of the numerical computation.
Figure 1 shows the calculated binding energy as a function of the mass number. For comparison, the related data from AME2020 [46] are also indicated by blue diamonds. The results of the experimental data are almost in agreement, which validates the calculations carried out by this study. Therefore, the RMF-CMR model can be successfully used to describe the stable nuclei among the Ti isotopes, and the pro model is valid for investigating other properties of neutron-rich nuclei, even close to the drip line. Moreover, the binding energy increases slowly as the neutron number increases, which means that the nucleon becomes increasingly softer.

Fig.2 (Color online)The two-neutron separation energies(S2n)with the RMF+CMR model are indicated by a blue circle as a function of the neutron number N.For comparison,the experimental data are also indicated by a black square.[46]
The two-neutron separation energy S2nis a physical quality in nuclear physics and is used for investigating the shell structure of a nucleon, as shown in Fig. 2. As is well known,the drip-line nucleon can be predicted by the value of S2n. As shown in Fig. 2, S2ngradually decreases as the number of neutrons increases.Specifically,the value of S2ndecreases abruptly when the neutron number N =40,which corresponds to the subshell.Notably,the shell gap is not obvious in72Ti with the traditional magic number N =50.Therefore,it is considered that the large N/Z ratio is the main contributor.Additionally,it is shown that S2nis close to the zero-scale line when N >50.The value of S2nis less than 0 MeV when N =58. Hence,78Ti is predicted to be the drip-line nucleon for the Ti isotopes. However,some experimental data do not support the shell structure,because the neutron number is equal to 40.For60-64Ti,the S2nvalues are significantly different to those of the RMF+CMR model. The three sets of experimental data exhibit linear decrease.The two former values are lower by more than 2 MeV compared with the theoretical calculation, and the last value is larger by 1.45 MeV. With the development of the radioactive isotope beam factory, isotones around neutron number 40 were first observed in 2020 [47, 48]. The experimental results revealed a deformed62Ti ground state. The Jahn-Teller effect is related to the increase in the two-neutron separation energies in the vicinity of62Ti. The large-scale shell model calculation reproduced the present measurement and disfavored the doubly-magic character of60Ca.
The single-particle spectrum is an important property for describing nuclear structures.In accordance with the CMR method reported in [41, 43], this study tested different contours,and the same momentum integration contour was selected for all Ti isotope nuclei. The selected contour is a triangular contour with the four key points k=0 fm-1,k=0.4-i0.4 fm-1, k=0.8 fm-1, and kmax=4.0 fm-1.To show the resonance states clearly in the triangular contour, the real axis Re k and imaginary axis Im k are truncated to 1.2 fm-1and 0.4 fm-1, respectively.


Fig. 3 (Color online) The single-particle spectra in 72-78Ti for the states occupied by the last neutron are presented in the complex momentum plane.The blue circle,black diamond,and brown triangle represent the continuum, bound states, and resonant states,respectively

Although not all bound states are drawn,the eigenstates occupied by the last neutron are presented, and their eigenenergies indicate that the last neutrons in72-76Ti are weakly bounded; therefore, these nuclei become increasingly softer as the number of neutrons increases.As can be seen, the energy level related to78Ti is positive, and the relevant width of 0.052 MeV can be obtained,which means that the last neutron is resonant and78Ti should not exist stably. As shown in Fig. 2, this study predicted that the drip-line nucleon of Ti is78Ti. The results of the two assessments are different but very similar.
To better investigate the exotic structure of the eveneven neutron-rich titanium isotopes, the single-particle levels of all nuclei (38 ≤N ≤56) are shown in Fig. 4 and are indicated by different colors. The quantum number of the last neutron of each Ti nucleus is also marked in the figure.The shell gap(3.562 MeV)of62Ti between levels 1/2[301] and 9/2[404] is more significant than that of the adjacent nuclei supporting the subshell structure(N =40).This result is consistent with the description of the twoneutron separation energy. Additionally, the quadruple deformation β2indicates the spherical structure of62Ti.For60-70Ti, the energy levels occupied by the last neutron increase with the isospin. However, the highest energy is lower than 0 MeV; therefore, these nuclei remain bound.With the further increase in the neutron number, the shell structure of72Ti is considered. Notably, a large shell gap does not exist between the 1/2 [440] and 5/2 [413] levels compared with that of72Ti. Hence, the traditional magic number (N =50) is not clearly shown. For74Ti and76Ti,the Fermi level is -0.400 MeV and -0.371 MeV,respectively.Therefore,these two nuclei are weakly bound.Moreover, the 5/2[413], 3/2[422], and 1/2[431] levels occupied the last neutron of74-78Ti, and these levels correspond to the 2d5/2level.
The nuclear radius is also an important parameter for investigating the characteristics of exotic nuclei. Figure 5shows the neutron RMS radii and the difference in the radii between the neutron and proton of titanium isotopes. As can be clearly seen, the neutron RMS radius increases monotonously with the isospin.According to the calculated data,a fitted dashed line is drawn in the top panel when the neutron number ranges from N =38 to N =48. The neutron RMS radius is approximately linear. However, for neutron-rich nuclei (50 ≤N ≤56 ), the data points of the neutron RMS radii are above the dashed line and further away.
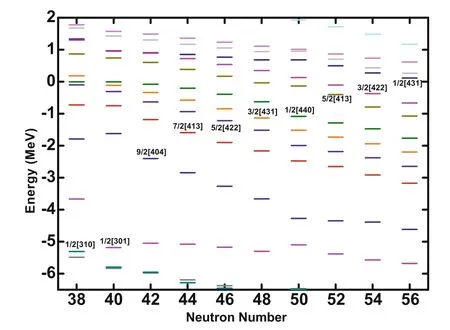
Fig. 4 (Color online) Energy levels as function of neutron numbers of Ti isotopes.For each nucleus,the energy level of the last neutron is indicated by the quantum number

Fig. 5 (Color online) Neutron RMS radii and radii difference of neutron and proton as function of neutron numbers of Titanium isotopes
The radii differences between the neutrons and protons are shown in the bottom panel.Similar to the neutron RMS radii, when the neutron number N is greater than 48, the properties of the neutron skin are determined by a rapid increase in the differences. Notably,72Ti is neutron-rich and exhibits a certain exotic character, although its magic number is 50. Thus, several novel points can be observed with regard to S2nand the radius. The radius increase in72Ti is attributed to the last energy level 1/2[440], where the radial density is slightly diffuse. Hence, the neutron skin phenomenon is particularly evident in70-78Ti.
The exotic phenomenon is reflected by the energy levels and RMS radius and is also illustrated by the diffuse spatial distribution. According to the wave functions obtained from the Dirac equation, the radial momentum probability distribution(RMPD) is shown for several states, including those occupied by the last neutron of72-78Ti in Fig. 6. To clarify the RMPD, the horizontal axis is cut at Re k=2 fm-1and the RMPD vanishes when Re k is more than 2 fm-1. Different single-particle levels are indicated by different colors. The density distributions of the last neutron and the other neutrons are expressed by solid and dashed lines,respectively.The background of the continuum is not shown in the figure. As can be seen, all states expand widely with an increase in momentum. In this figure, the blue solid line is the δ function,which gives the eigenstate occupied by the last neutron in78Ti. In complex momentum space, the radial momentum probability distributions for both the resonant states and bound states converge.

Fig. 6 (Color online) Radial-momentum density distribution for several states of 72-78Ti. The solid and dashed lines indicate the eigenstates occupied by the last neutron and the other neutrons,respectively

Fig. 7 (Color online) Radial density distribution in coordinate representation. The solid lines indicate the eigenstates occupied by the last neutron; the dashed lines indicate states with a lower energy leve
The density distribution in the coordinate representation,after the wave functions are transformed into a coordinate plane, is also considered. In Fig. 7, the radial density distribution for72-78Ti is shown as a function of coordinate r.Similar to Fig. 6, the different colors indicate different energy levels. The solid lines represent the eigenstates occupied by the last neutrons of the four nuclei. The three dashed lines in each panel indicate other lower levels.Obviously, almost all lines decrease to zero at the edge of the box (r =15 fm). However, the blue solid line for the density distribution of eigenstate 1/2[431] of78Ti does not converge at the border, which matches the characteristics of the resonant states. By combining the energy values shown in Fig. 4, the diffuse density distribution confirms that78Ti is not a stable nucleus. Therefore,76Ti is the last stable nucleus in the Ti isotopic chain.
4 Summary and prospective
This study investigated even-even titanium isotopes using the RMF-CMR method. The deformed self-consistent potential was derived within the RMF framework and was then used to investigate the resonant states in the CMR model. First, the binding energies of52-64Ti are in good agreement with the data in AME2020. The S2nvalue obtained from the binding energy reproduced the magic number N =40. However, the traditional magic number N =50 shell gap is not obvious.Moreover,the value of S2npredicts that78Ti is a drip-line nucleon for Ti isotopes. In the complex momentum plane, the bound states and resonant states are displayed and distinguished from the continuum. A subshell structure (N =40) is observed in62Ti based on the large energy gap, and the traditional magic number(N =50)disappears owing to the large N/Z ratio in72Ti. The shape of62Ti is approximately spherical, and72-78Ti is obviously deformed. The RMS radii of60-70Ti increase linearly, whereas the RMS radii of72-78Ti increase abruptly. These energy levels and the RMS radii indicate that72-76Ti is weakly bound, while78Ti is resonant.Finally,the radial density distributions in the complex momentum plane and coordinate space were presented based on the calculated wave functions. The radial distribution of the resonant states in78Ti in the coordinate representation is slightly diffuse. Based on these two assessment criteria, this study predicted that the drip-line nucleus of the Ti isotope is78Ti or76Ti.
Satisfactory results were obtained for the titanium isotopic chain using the RMF-CMR method, and this is the first time that the resonant state has been investigated using the CMR model and self-consistent potential. The development of a CMR model is important,and future work will consider the pairing correlation in this theoretical formalism. Tensor interactions [49] or Jahn-Teller effects may also help in elucidating the experimental phenomena and the edge of the nuclear chart.
Author ContributionsAll authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Tai-Hua Heng and Yao-Wu Chu.The first draft of the manuscript was written by Tai-Hua Heng and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
杂志排行
Nuclear Science and Techniques的其它文章
- Hard X-ray focusing resolution and efficiency test with a thickness correction multilayer Laue lens
- Monte Carlo study of the neutron ambient dose equivalent at the heavy ion medical machine in Wuwei
- Experimental investigation on the characteristics of molten lead–bismuth non-eutectic alloy fragmentation in water
- Configurational information entropy analysis of fragment mass cross distributions to determine the neutron skin thickness of projectile nuclei
- Differences in MBUs induced by high-energy and medium-energy heavy ions in 28 nm FPGAs
- Thin-film approximate point scattered function and its application to neutron radiography
