不同级配颗粒材料的循环硬化行为与能量耗散*

夏平心 邓 文 邵龙潭

(①常州大学城市建设学院，常州 213164，中国)(②东南大学土木工程学院，南京 211189，中国)(③大连理工大学工程力学系，大连，116024，中国)

0 引 言

循环荷载是岩土工程基础遭受的最常见的载荷，可能导致岩土基础结构强度下降(Wichtmann et al.，2005;Karg et al.，2009)、不规则沉降(Puppala et al.，2009;Dong et al.，2018)、路面开裂(Roesler et al.，2005)和路堤肩侧向剪胀(Yapage et al.，2014)，从而降低路基的运行生命周期(Wichtmann et al.，2005;Karg et al.，2009;Frost et al.，2014;Bian et al.，2018;Costaa et al.，2018;Zhai et al.，2020;Xia et al.，2022)。颗粒材料(土体)在循环载荷下表现出逐渐硬化的行为，主要体现为应力-应变滞回曲线逐渐变陡(Zeng et al.，2016;Xia et al.，2021b)，变形模量随着循环的进行逐渐变大(Xia et al.，2021c)，颗粒接触体系逐渐变得稳定(Xia et al.，2021a)。因此，充分认识颗粒材料的循环硬化行为，揭示其变形机理对保障遭受循环荷载的岩土结构安全运行具有重要意义。学者们针对颗粒材料在循环荷载下的变形行为做了大量的研究，然而关于循环硬化行为的宏-微观相对应的机理解释的研究却不多见，这对探索颗粒材料安定性机理具有启发意义。

颗粒材料的变形行为与颗粒级配密切相关。颗粒级配对颗粒材料的变形模量、强度、压缩性等力学特性具有显著影响。对于级配良好的颗粒体系具有充足的细粒填隙、压实位移较大、配位数高、内摩擦角大等特点。针对这些特点很多研究学者从宏观尺度或颗粒尺度(微观尺度)开展了相关的研究(Xu et al.，2013;Chen et al.，2016;Le et al.，2018)，试图从宏观或微观角度对其内在机理进行解释。然而，关于不同级配颗粒体系在宏-微观尺度上相对应的机理研究却不多见，特别是颗粒滑动、循环硬化、能量耗散之间的关联机制的研究鲜见报道。

离散单元方法(DEM)(Cundall et al.，1979)是一种新兴的数值方法，以其对颗粒材料变形机理的洞察而闻名(Zamani et al.，2011;赵洲等，2019)。近年来，它被认为是研究颗粒材料模量/刚度极具有前景的工具(Agnolin et al.，2007；Magnanimo et al.，2008；Gu et al.，2013a，2013b)，并取得了丰硕的研究成果(Magnanimo et al.，2008；Gu et al.，2013a，2013b)，促进了对颗粒材料变形规律的理解(Cundall et al.，1989；Gu et al.，2013a，2013b;杨忠平，2020)，弥补了室内试验难以在微细观尺度上研究的不足。DEM不仅能获取颗粒接触体系的内变量演化规律，而且能统计颗粒体系内的各能量的转化，特别是由于颗粒滑动造成的能量耗散。

本文通过3D-DEM实施了循环三轴数值模拟试验，研究了不同级配下颗粒体系在循环荷载下的循环硬化行为，并讨论了(轴向)平均模量和由滑动接触造成的能量耗散的演化趋势。

1 循环三轴试验模拟

1.1 数值试样

本文使用DEM 商业软件 PFC3D(Itasca，2008)进行数值模拟。在PFC3D中，颗粒体系是用刚性球通过软接触彼此相互作用来建模的，并假设球体只有有限的刚度。通过允许颗粒体重叠来模拟接触处的接触。应用牛顿第二运动定律于每个颗粒，不断更新颗粒的位置，并根据力-位移定律，更新每个接触的信息。

试样由一个圆柱体空间表示，高度h0=2.4mm，直径d0=1.2mm，如图1a所示。数值试样采用半径膨胀法制备。一对刚性墙用于模拟上下移动的加载板来压缩试样，而圆柱形刚性墙通过伺服控制收缩和扩张以保持恒定的围压。土颗粒用球体表示，颗粒级配曲线如图1b所示。模拟采用了6种颗粒级配，分别考虑相同不均匀系数Cu而颗粒平均粒径d50不同和相同颗粒平均粒径d50而不同不均匀系数Cu两类工况。

图1 (a)数值试样和(b)试样颗粒级配曲线Fig.1 (a) Specimen in DEM simulator and (b) grain size distribution curve of numerical specimen

1.2 颗粒接触模型与输入参数

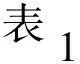
图2 数值模拟中颗粒接触模型示意图(g是颗粒表面间距，Dn和Ds分别表示法向和切向黏壶)Fig.2 Schematic diagrams of rolling resistance linear contact model(g is the surface gap(non-tension joint)，Dn and Ds are the normal and shear dashpots)

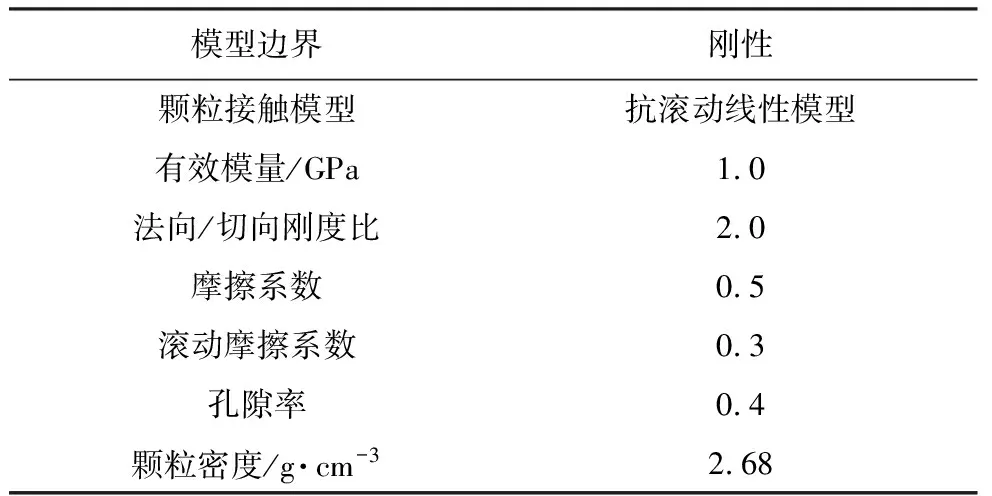
表 1 DEM模型中输入参数Table1 Microscopic parameters in DEM

1.3 数值模拟过程

数值试样在各向同性压力下压实，达到给定的目标围压σ3=100kPa，并通过伺服控制始终维持不变。随后，顶部和底部压板以每1000步 3.5×10-5的恒定应变速率相向移动直到达到目标应力值，时间步长为10-8s。最小和最大偏应力分别设置为10kPa和100kPa，循环数统一设置为200次。

2 数值模拟结果与讨论

2.1 滞回应力-应变曲线

图3 循环荷载下典型的应力-应变曲线Fig.3 Typically stress-strain curve in cyclic loading

图4 循环荷载下能量耗散演化Fig.4 Evolution of energy dissipation during cyclic loading

以GS1试样为例，其应力-应变关系的模拟结果如图3所示。随着循环次数的增加，滞回圈逐渐变小并趋于闭合。前几个应力循环产生较大的应变增量，随着后续应力循环的进行，应变增量逐渐减小，这与其他文献中室内试验和模拟结果一致(Indraratna et al.，2010；Nguyen et al.，2014；Chen et al.，2015)。此外，应力-应变滞回行为表明能量耗散不断累积。图4显示了能量耗散的累积过程，放大细节展示在插图中见图4。结果表明无论加载或卸载，能量耗散都会持续累积。然而，单个循环周期内的能量耗散增量逐渐降低并且趋于常数。数值模拟过程通过应变累积和能量耗散一致再现了循环荷载下颗粒材料的循环硬化行为，为研究岩土基础在循环荷载下，特别是慢速往复荷载下，比如，大坝蓄水泄洪、建筑物堆载与迁移、慢速交通荷载等，有益于从能量耗散角度来认识结构循环硬化和变形沉降问题。

2.2 变形模量演化

循环硬化行为由加载期间的平均变形模量(峰-峰连线的斜率)进一步展示，如图5所示，结果表明随着循环荷载的进行，平均模量逐渐增加并趋于渐进值。根据文献(Xia et al.，2021a)中的建议，平均变形模量用如下函数拟合：

(1)

式中：αE是模量变化系数；Ee表示为模量的渐进值。拟合结果如图5所示。需要注意的是，图5中的数据点离散型比较大，尽管拟合函数的R2不是很高，但在数据演化趋势上，与拟合函数呈现一致；而且不同颗粒级配下的拟合指数相差不大，约为0.6左右。然而，模量的渐进值Ee和模量变化系数αE却明显依赖于颗粒级配，如图6所示。图中结果表明模量的渐进值Ee和模量变化系数αE随着不均匀系数Cu的增加而降低，而随着d50的增加却出现了增加的趋势，即颗粒材料不均匀系数越低，颗粒的平均粒径越大平均模量越大。

2.3 滑动接触演化

循环荷载造成颗粒间的重新排列，并产生更为致密的颗粒结构。当颗粒重新排列时，颗粒间形成新的接触网络以及新的接触力分布。循环硬化过程中，接触具有的潜在相对运动状态可以用流动性m来描述(Xia et al.，2021a)：

(2)

式中：Fs和Fn是接触的切向力和法向力。当m接近1时，该接触接近滑动状态，特别是当m=1时则发生滑动。相反，m的值越小(或接近0)，接触越难达到滑动状态。因此，数值试样中m的分布反映了颗粒的接触力网络状态。将m的取值范围细分为5个等区间，统计每个区间的接触数，则落于每个区间的概率为：

(3)

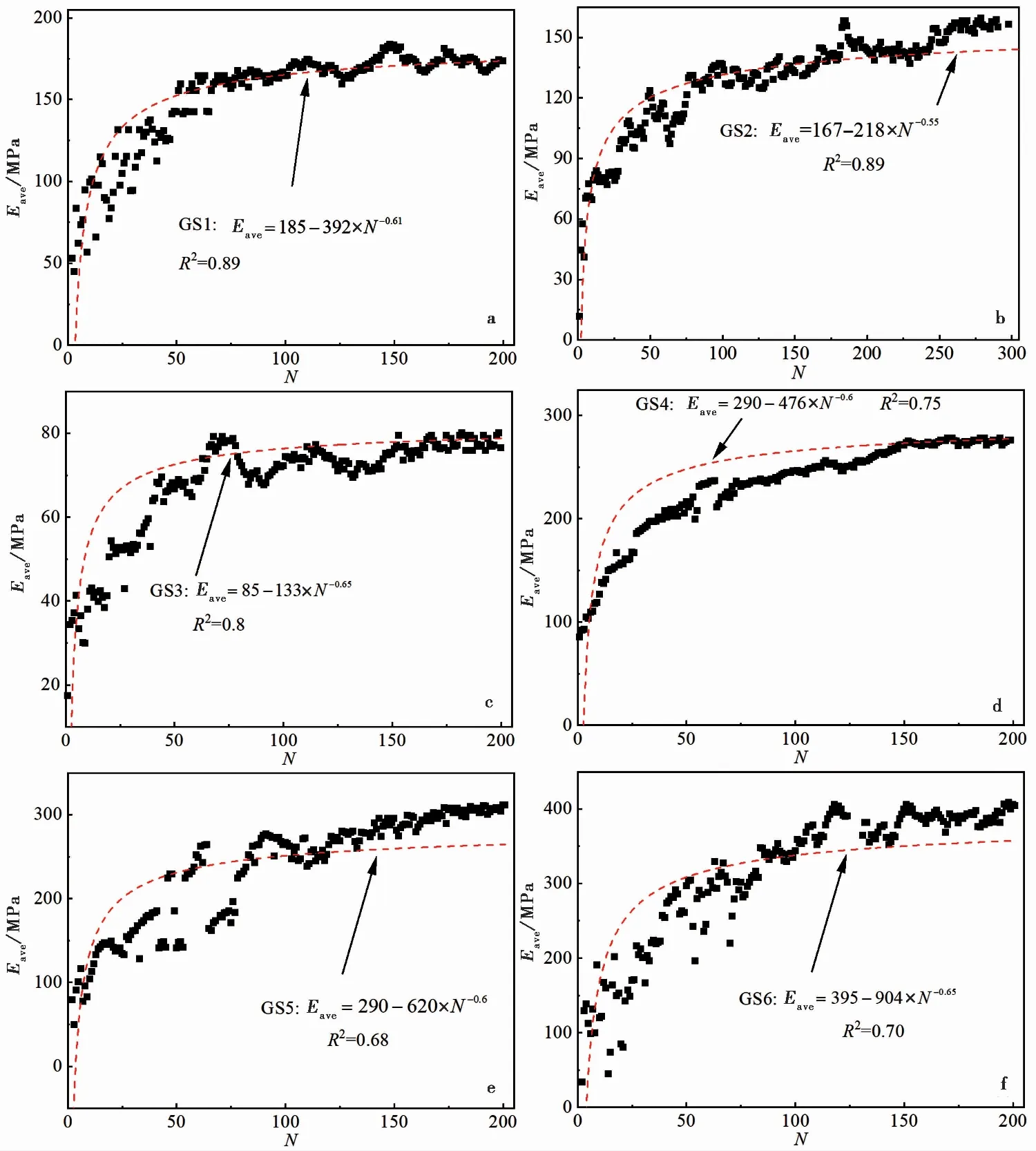
图5 循环荷载下平均模量的演化(a)～(f)：GS1～GS6Fig.5 Evolution of average modulus with cycles(a)～(f)：GS1～GS6

图6 不均匀系数和平均粒径与参数Ee和αE的关系Fig.6 Relation of Ee and αE with uniformity coefficient and mean particle diameter

图7 Pi随时间步的演化(a)～(f)：GS1～GS6Fig.7 Evolution of Pi with time steps (a)～(f)：GS1～GS6

2.4 能量耗散演化

应变累积率的降低表明每个循环中的能量耗散占比减少。在循环加载期间，外部加载提供的总边界能转化为颗粒动能、存储在接触处的应变能、颗粒间的摩擦耗能，以及其他耗散机制耗散的能量(Nguyen et al.，2014)。总应变能Ek是在所有接触Nc上对应变能求和，每个时间步的耗散能ΔEu是在滑动接触Ncs上对耗散能求和(Itasca，2008，Jiang et al.，2015，Tong et al.，2021)，即：

(4)

(5)

式中：Eu0、Fs′和Δδu分别是时间步开始时的能量耗散、时间步开始时的接触切向力和一个时间步内接触的相对滑动位移增量。t0和t分别是循环加载期间的开始和持续时间步长。

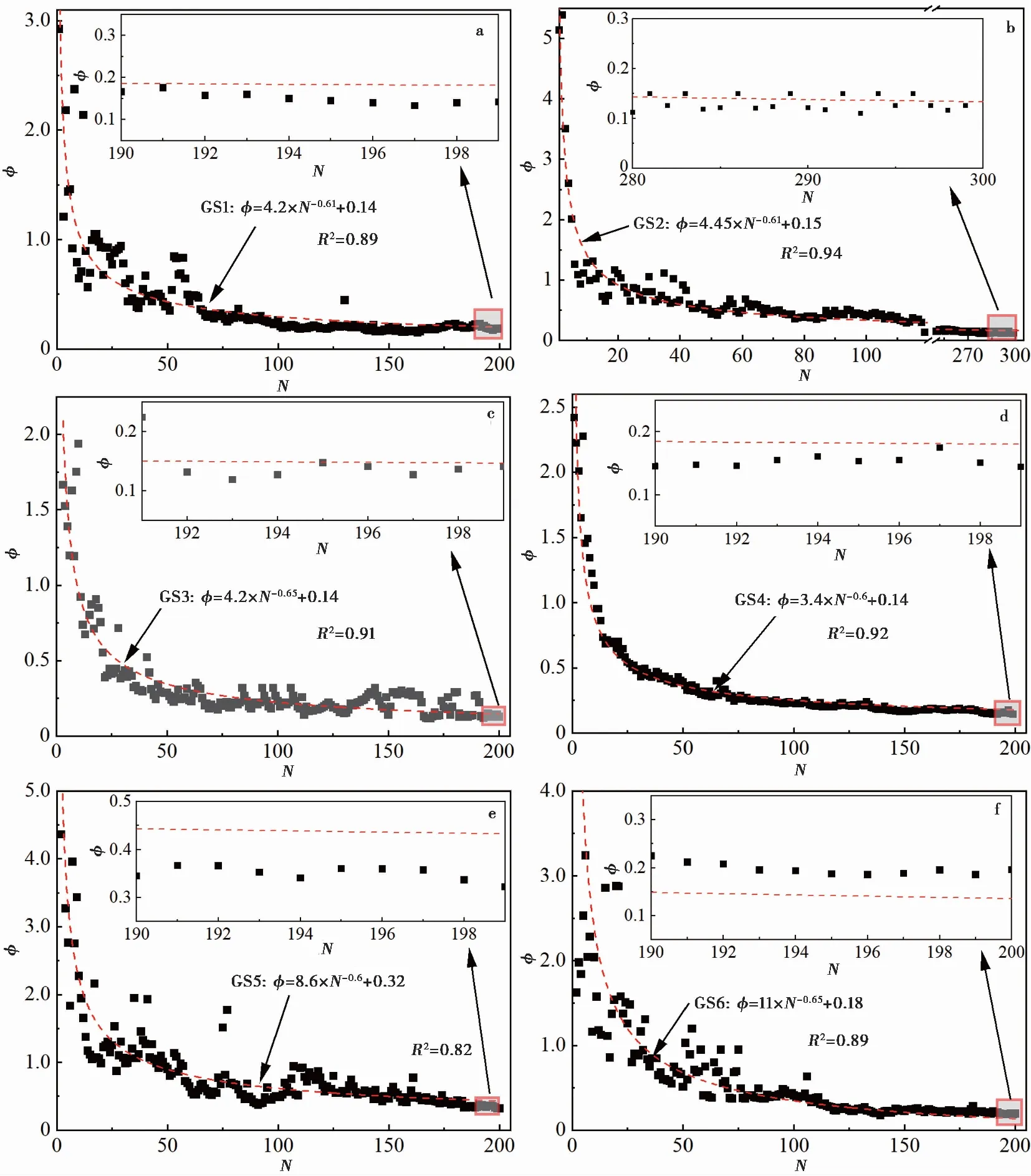
图8 归一化能量耗散随循环数的演化(a)～(f)：GS1～GS6Fig.8 Evolution of normalized energy dissipation with cycles(a)～(f)：GS1～GS6

能量耗散是颗粒滑动的宏观表现。每个应力循环中的能量耗散份数由归一化能量耗散φ描述，定义为φ=ΔEu/ΔEk，其中ΔEu是加卸载循环后的能量耗散增量，ΔEk是加卸载循环期间的应变能幅值，即峰值-峰值的应变能增量。需要注意的是，能量耗散是单调增加的，而应变能在加载过程中累积，在卸载过程中释放。归一化能量耗散随加载循环数的演变如图8所示，结果表明随着循环数的增加，能量耗散逐渐降低，其演化行为与平均模量的演化行为近似一致。参考式(1)则φ随N的演化趋势用如下函数拟合：

(6)

式中：βφ是能量耗散衰减系数。拟合结果如图8所示。φ随加载周期的增加不断较小，表明随着应变硬化的加强，能量耗散占比逐渐减小。由拟合函数可以看出，能量耗散不会一直衰减，存在一个阈值，约为0.15。该阈值可以定量描述最终状态下能量耗散的占比，即颗粒体系经过大量的循环荷载后进入变形稳定状态或安定状态，体现出通常认为的“弹性”行为时，仍然伴随着能量的损耗。理论上纯弹性行为是没有能量耗散的，然而对于颗粒材料来说通常认为的纯“弹性”行为是不存在的，因此，对于颗粒材料展示出的变形可恢复同时伴随着能量损耗的力学行为近似为“准弹性”行为(Xia et al.，2021a)。颗粒材料使用“准弹性”概念在描述一些特殊现象时比较方便，比如解释砂土卸载体胀(Xia et al.，2021c)，值得进一步探讨。

图9 βφ随不均匀系数和颗粒平均粒径的变化Fig.9 Variation of βφ with uniformity coefficient and mean particle diameter

能量耗散衰减系数βφ随不均匀系数和颗粒平均粒径的变化如图9所示，其随不均匀系数的变化趋势并不明显，但随颗粒平均粒径的增加而增大，表明颗粒平均粒径越大的颗粒体系越早完成能量耗散过程，即循环硬化过程越快完成。值得注意的是能量耗散衰减指数的大小与图5中平均模量呈现的相近，表明在描述循环荷载硬化行为时，无论是使用变形模量还是归一化能量耗散在结果上是一致的。这一结论在研究颗粒材料安定性微观机理时具有启发意义。这是因为颗粒材料安定性的定义和判定准则常由应变累积趋势来定，而应变累积趋势对应着模量的演化过程。因此，从能量耗散以及颗粒滑动等方向探索颗粒材料安定性机理不失为一种新的选择。

3 结 论

本文通过实施3D-DEM数值模拟研究了不同级配下颗粒材料在循环荷载下的循环硬化行为，并分析了(轴向)平均模量和能量耗散的演化趋势。结果表明随着循环荷载的进行，平均模量逐渐增加并趋于渐进值。模量的渐进值Ee和模量变化系数αE随着不均匀系数的增加而降低，而随着d50的增加却出现了增加的趋势，即颗粒材料不均匀系数越低，颗粒的平均粒径越大，平均模量越大。单个循环的能量耗散随着循环数的增加不会一直衰减，而是存在一个阈值，约为0.15，即颗粒材料在循环荷载下始终伴随能量耗散，该阈值可以定量描述最终状态下的能量耗散占比。能量耗散衰减系数βφ随不均匀系数的变化趋势并不明显，但随颗粒平均粒径的增加而增大，表明平均粒径越大的颗粒体系越早完成能量耗散过程，即循环硬化过程越快完成。平均模量增加指数和能量耗散衰减指数的大小相近，表明在描述循环荷载硬化行为时，无论是使用变形模量还是归一化能量耗散在结果上是一致的。