热电子注入效率影响因素的仿真研究

李旺豪，杨 婷，张 震，桑胜波，菅傲群

(太原理工大学 a.微纳系统研究中心，b.新型传感器与智能控制教育部和山西省重点实验室，太原 030024)

热电子指的是在金属微纳结构中吸收外界能量后跃迁到更高能级的高能电子，热电子注入即高能热电子越过金半接触界面到达半导体导带的过程。热电子注入效应可将光能转化为化学能、电能，广泛应用于光电催化以及光电探测器件等研究领域[1-2]。贵金属微纳结构中的局域表面等离子体共振(LSPR)效应能够极大地提高热电子的产生效率[3]。表面等离子共振是金属表面的电子集体震荡，能够有效地增强金属吸收光子能量激发产生高能电子空穴对。因此，贵金属微纳结构与半导体组合形成的等离子光催化材料受到许多科研人员的青睐[1-4]，该结构不仅改善了常规半导体光催化剂中电子空穴对快速复合的缺陷，还能够有效拓宽其光响应范围[5-6]。提高热电子注入效率对等离子体光催化结构的性能有着重要影响。

近年来，有不少关于仿真计算热电子注入效率的研究，大致可分为3类：FOWLER[7]和SPICER[8-9]提出的热载流子注入三步模型首次尝试量化热载流子的发射过程，该理论模型主要应用于计算块状金属结构的光电探测器件，包含能带弯曲、热载流子产生、传输和发射过程的仿真，Fowler模型是一套完整的理论，但近似理想条件较多，对热电子注入过程大幅度的简化；GOVOROV et al[10]提出的等离子体纳米结构的动力学密度泛函理论，基于密度矩阵的动力学方程，运用量子理论计算了光激发载流子在金属纳米粒子中的分布，进一步发展了Fowler理论，研究了金属纳米颗粒尺寸、形貌以及激发光偏振对热载流子注入效率的影响[11]，但该理论模型并未包含热载流子寿命对热电子注入过程的影响；ALEJANDRO et al[12]将金属纳米颗粒中传导的电子描述成有限球形势井中的自由粒子，并使用费米黄金定律计算等离子体激发产生的热载流子，这为热载流子产生过程的全面理论描述提供了新的方案，探讨了不同粒径的贵金属纳米颗粒以及热载流子寿命对热电子注入效率的影响，但该理论是将热载流子的寿命作为影响因素来进行直接讨论的，缺少对热载流子寿命的计算。

综上所述，上述已建立的计算模型计算过程复杂，都或多或少的具有某一方面的缺陷，同时由于缺乏实验验证，客观上也阻碍了热电子注入效应理论计算模型的进一步完善。本文以Fowler理论模型为基础，综合考虑热电子寿命以及金半接触界面动量匹配对热电子注入过程的影响，建立物理过程完善的计算模型，仿真计算热电子注入效率，为设计先进的等离子光催化材料提供理论指导。另外，通过文献调研，热电子注入效率的主要影响因素包括贵金属纳米颗粒的种类、尺寸、形状、金属与半导体的接触面积、肖特基势垒高度、入射光照强度和波长、入射光子能量、温度等[11，13-15]。由于篇幅限制，本文将聚焦于研究入射光子能量、贵金属纳米颗粒尺寸、以及肖特基势垒高度3个因素对热电子注入效率的影响。

1 理论模型

1.1 假设前提与通用参数

热电子注入效率是基于一定的理想条件和模型进行计算和仿真的，下面列出必要的假设前提[2,12,16-17]：

1) 假设在可见光照下，贵金属纳米颗粒表面产生的电场是均一的。

2) 忽略其他散射过程对热电子产生的贡献，仅考虑LSPR效应激发产生的热电子。

3) 忽略多体效应，假设一个等离子体仅激发产生一对热电子空穴对，且热电子激发的能量恒为一个光子的能量。

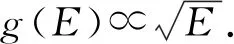
5) 假设在贵金属纳米颗粒中激发产生的热载流子位置是随机且均匀分布的。

6) 电子在吸收光子能量前处于热平衡的状态，且光子的能量恒定为hω.

另外，计算过程中通用的物理常量，对应的符号和选取的参数值，如表1所示。

表1 仿真通用参数的符号和取值

1.2 热电子注入三步模型

图1展示了典型的金属半导体接触产生的能带结构，由于费米能级的差异，半导体与金属在接触时引起的电子转移会产生能带弯曲，并在金半接触界面产生肖特基势垒。热电子注入过程可大致分为3个部分，具体描述如下：在可见光照下，由于贵金属纳米颗粒的LSPR效应，金属微纳结构中的表面等离激元吸收光子能量激发产生高能热电子，该过程被称作热电子的产生；激发产生的热电子的位置在金属微纳结构中是随机分布的，只有平均自由程大于产生位置到金半接触界面距离的热电子才有机会到达金半接触界面，该过程被称作热电子的传输；到达金半接触界面的电子在垂直金半接触界面方向上的动能必须大于肖特基势垒高度才能越过肖特基势垒，同时还必须满足动量匹配，该过程被称作热电子的发射。因此，计算热电子注入效率的关键在于量化上述热电子的产生、传输和发射3个过程[17-18]。

图1 热电子注入三步模型示意图

1.3 热电子的产生

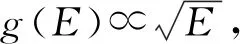
D(E)=

(1)

1.4 热电子的传输

热电子产生之后能否到达金属半导体接触界面与热电子的寿命相关，只有寿命足够长的热电子才有可能到达界面，即热电子的平均自由程大于热电子产生位置到金半接触界面的距离。因此，量化热电子传输过程的关键在于热电子平均自由程的计算，而热电子平均自由程的大小与热电子的能量相关[20]：

(2)

对于球形金属纳米粒子，具有能量E的热电子到达金属半导体接触界面的概率为[16]：

(3)

式中，R是纳米粒子的半径，向量R(θ)是指从原点指向纳米粒子表面上一个点的向量，r是热电子产生的位置，θ是r和R之间的角度，即到达金半界面的最短路径与热电子实际所走路径之间的角度。

1.5 热电子的发射

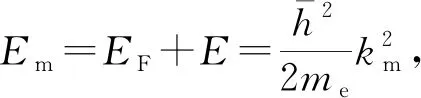
(4)

除此之外还需要考虑金属-半导体界面处的反射的可能性，这是由于热电子在两种介质中的动量不匹配而产生的，由金半接触界面的转移系数XT决定[18]：

(5)

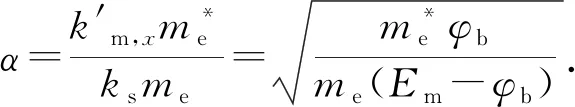
1.6 热电子注入效率

综合上述分析的热电子产生、传输和发射过程，热电子注入效率可用下式描述：

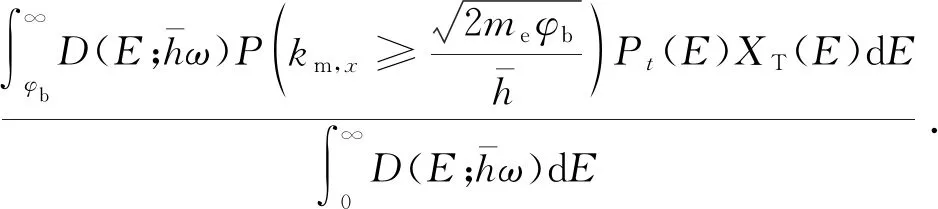
(6)

2 热电子注入效率影响因素及其仿真结果讨论

2.1 入射光子能量

在仿真计算过程中，为了保证入射光子能量作为单一的变量，取贵金属纳米颗粒的半径为10 nm，肖特基势垒高度为1 eV.仿真计算了入射光照波长(430，470，520，590，680，780 nm，对应的入射光子能量为2.89，2.64，2.39，2.10，1.82，1.59 eV)对热电子注入效率的影响，仿真结果如图2所示。

基于上述的热电子注入三步模型，在其余条件不变的情况下，入射光子能量仅会对热电子的产生过程造成影响，贵金属纳米颗粒吸收光子能量激发产生热电子，入射光子能量越大，激发产生的热电子能量越高。式(1)在不同光子能量条件下对热电子能量分布影响的仿真结果如图2(a)所示。为使在每个波长条件下热电子的产生总量一致，每条曲线都经过归一化处理，使得每条曲线下的面积是相等的。需要注意的是，只有能量高于肖特基势垒(1 eV)的热电子才有机会越过肖特基势垒，对应于每条曲线下灰色的部分，该面积的大小随着光子能量的增长而增长，证实了随着入射光子能量的增加(入射波长蓝移)，高能热电子所占比例也随之上升，该结果与WHITE et al[19]的研究成果(当入射光子能量大小与肖特基势垒高度近似时，具有足够能量越过肖特基势垒的热电子所占比例较小，且该比例随着入射光子能量的增加而增加)一致。进一步的，图2(b)是光子能量对热电子注入效率(式(6))的影响，热电子注入效率随着入射光子能量的提升而升高，2.89 eV入射光子能量条件下的热电子注入效率相对于1.59 eV条件下已经提升了将近2.3倍。NG团队[18]研究结果表明当入射光子能量稍大于肖特基势垒时，热电子注入效率快速增长，随后热电子注入效率随着入射光子能量的增加而缓慢增长，这与图2(b)所展示的变化趋势相同。这个结果与图2(a)得到的结论是一致的，因为电子在金属纳米颗粒中的初始能量分布是一致的，入射光子能量越大，激发产生的热电子所具有的能量越高，能够穿过肖特基势垒的概率越大，热电子注入效率也随之提升[18,20-21]。

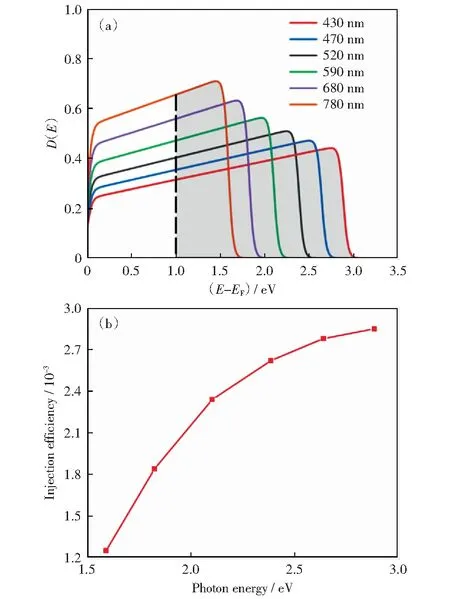
图2 入射光子能量对激发热电子能量分布以及热电子注入效率的影响

2.2 贵金属纳米颗粒尺寸

贵金属纳米颗粒作为等离子光催化结构中重要的组成部分，其对热电子注入效率的影响非常关键，例如贵金属纳米结构的形状、尺寸、种类对热电子注入效率都存在相当大的影响，这一节将重点分析贵金属纳米颗粒尺寸对热电子注入效率的影响。取入射光照波长为520 nm，肖特基势垒高度为1 eV，仿真计算了半径为5，10，15，20，25，30 nm的贵金属纳米颗粒对热电子注入效率的影响，仿真结果如图3所示。

在热载流子传输过程中，只有热电子产生位置到金半接触界面的距离小于平均自由程的热电子才能到达金半接触界面，因此贵金属纳米颗粒的尺寸变得尤为重要，尺寸越大的贵金属纳米颗粒中产生的热电子能够到达金半接触界面的比例越小(假设热电子在贵金属中产生位置是随机分布的)，因为热电子在到达金半接触界面的过程中可能会发生散射。如图3(a-c)所示为式(3)在不同粒径的贵金属纳米颗粒条件下对热电子传输概率的仿真结果，随着贵金属纳米颗粒半径的增加，热电子传输概率的下降趋势极其明显。值得一提的是，热电子的平均自由程的大小与能量是相关的，并且平均自由程随着能量的增长而减小，因此同一尺寸的贵金属纳米颗粒的热电子传输概率随着能量的增长有下降的趋势。

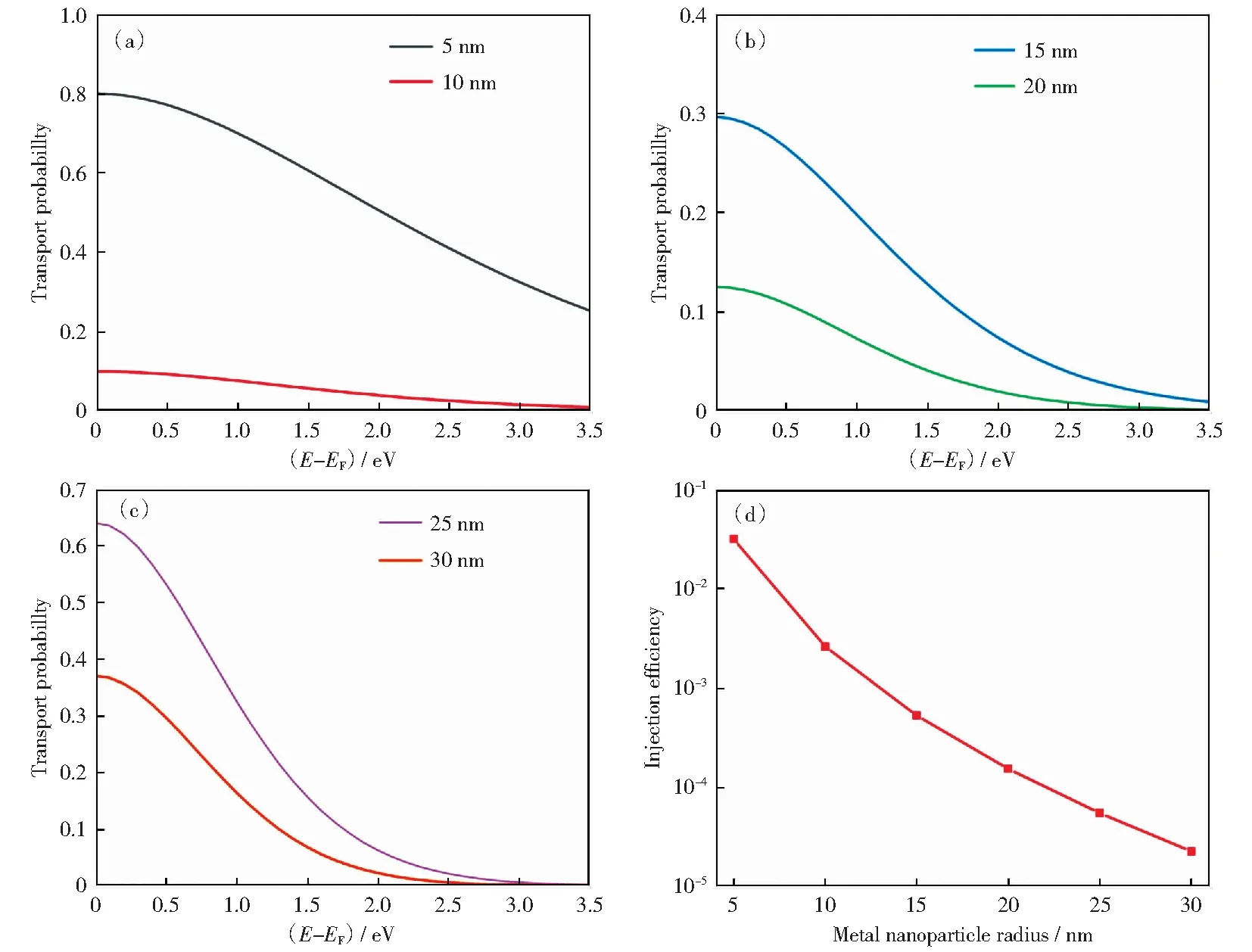
图3 不同尺寸的贵金属纳米颗粒对热电子传输概率和热电子注入效率的影响

贵金属纳米颗粒的尺寸对热电子注入效率的影响如图3(d)所示，热电子注入效率随着贵金属纳米颗粒尺寸的增长而下降。图3(d)纵坐标用对数表示，从半径为5 nm的贵金属纳米颗粒增长到30 nm，热电子注入效率下降超过了3个数量级。另外，从仿真结果可知半径为5 nm左右的贵金属纳米颗粒具有最佳的热电子注入效率。ALEJANDRO M教授的研究表明，半径为5 nm的贵金属纳米颗粒具有最高的热电子产生效率[12]，GOVOROV教授也报道过对于金纳米晶体，有效产生高能热电子的最佳尺寸(立方晶体边长)为10～20 nm[10]，这些结论与本文的仿真结果类似。热电子的平均自由程与热电子的能量相关，而贵金属纳米颗粒的尺寸对热电子的产生位置有很大的影响，半径越小的贵金属纳米颗粒中激发产生的热电子到金半接触界面的距离也越小，因此对于具有相同能量的热电子，其到达金半接触界面的传输概率越大，故热电子注入效率越高[10-11]。

当然在实际光电探测设备设计时，并不是尺寸越小的贵金属纳米颗粒越好，因为尽管尺寸小的贵金属纳米颗粒具有较高的热电子注入效率，但是由于其体积有限，热电子的产生总量有限，其热电子注入电流的大小也会相应地受到限制，因此需要权衡热电子注入效率和热电子产生总量直接的关系，得到最佳的贵金属纳米颗粒尺寸。

2.3 肖特基势垒高度

到达金半接触界面的热电子能否越过肖特基势垒需要考虑动量大小和动量匹配的问题，在热电子发射过程中最关键的影响因素是肖特基势垒的高度，其大小直接决定了热电子能否越过金半接触界面，因此研究肖特基势垒高度的影响是非常有必要的。取入射光照波长为520 nm，贵金属纳米颗粒的半径为10 nm，仿真计算了肖特基势垒高度(0.3，0.6，0.9，1.2，1.5，1.8 eV)对热电子注入效率的影响，仿真结果如图4所示。

热电子在到达金半接触界面后，只有其垂直金半接触界面的动量分量高于肖特基势垒的高度才能越过肖特基势垒进入半导体的导带。如图4(a)所示为式(4)在不同肖特基势垒高度条件下热电子发射效率的仿真结果，热电子在同等的能量下，肖特基势垒越低，热电子热发射效率越高。另外，热电子的发射效率随着热电子能量的增长而提高。肖特基势垒高度对转移系数(式(5))的影响如图4(b)所示，与热电子发射效率的规律基本上相符，肖特基势垒高度越低越能够允许能量更低的热电子穿过金半接触界面。另外，势垒高度小的曲线下的归一化面积越大，这表示能够满足能量条件的热电子的数量越多。综合来看，肖特基势垒对热电子注入效率的影响如图4(c)所示，热电子注入效率随着肖特基势垒高度的升高而下降，产生这种结果是上述两种原因(发射效率和转移系数)导致的。1.2 eV肖特基势垒高度条件下的热电子注入效率相对于0.3 eV条件下的热电子注入效率几乎下降了4倍之多，另外，当肖特基势垒高度达到1.5 eV之后，热电子注入效率几乎趋近于0.总而言之，肖特基势垒高度越高，热电子穿过势垒所需的能量越高，热电子注入效率越低。需要知道的是，并不是肖特基势垒高度越低越好，热电子发射进入半导体一侧的概率虽然高，但是同样的，电子与空穴复合的概率也随之增加了。

图4 肖特基势垒高度对热电子发射效率、金半界面处的转移系数及热电子注入效率的影响

3 结论与展望

本文基于Fowler理论模型，以热电子三步过程为基础，综合考虑热电子寿命以及金半接触界面动量匹配理论，建立了一套较为完整的量化热电子注入效率的仿真模型。基于此理论模型，仿真计算了入射光子能量、肖特基势垒高度以及贵金属纳米颗粒对热电子注入效率的影响。仿真结果发现：入射光子能量和热电子注入效率之间存在正向关系、半径为5 nm左右的贵金属纳米颗粒具有最佳的热电子注入效率、热电子注入效率随着肖特基势垒高度的升高而降低。

虽然本文建立了热电子注入效率的计算模型，但在实际等离子光电探测器件设计时，热电子注入效率的量化与计算更为复杂，系统参数往往互相影响。以贵金属纳米颗粒的尺寸为例，改变尺寸不仅会影响热电子传输过程，还会影响贵金属态密度、贵金属光吸收波长、以及纳米颗粒之间的散射情况等多个参数，从而影响热电子的注入效率。因此这种更加复杂且贴合实际情况的理论模型是今后研究热电子注入理论的一种趋势，但是建立更精细的理论模型需要理论进步，同时离不开实验结果的支撑和验证。本文的仿真模型对于热电子注入过程的理论简化和热电子注入效率的计算提供了仿真模型，为实验验证奠定了基础，同时为等离子光催化剂和光电器件的设计提供了理论指导。