基于粒子群算法的高温高压三轴试验机控制系统优化

2022-11-19孟巧荣李亚军

太原理工大学学报 2022年6期

林峰，孟巧荣，b，李亚军，陈涛，李明

(太原理工大学 a.矿业工程学院，b.原位改性采矿教育部重点实验室，太原 030024)

岩石力学的发展始终伴随着试验机的发展而逐渐发展、成长和成熟[1]。然而在岩体高温高压实验过程中，随着温度的升高，岩体会发生物理化学变化，影响岩体的实际承压状况，另外，传热传质也会使岩体温度发生波动。因此，岩体高温高压实验过程中，压力和温度随时间的波动较大，对试验机的温度和压力需要实时控制。试验机控制系统的升级优化是必不可少的。岩石力学特性的不同，三轴加载液压伺服系统对岩石压力的影响而不同。每次试验的岩石具有不同的负载质量和负载刚度，液压系统的稳定性随力学特性的不同而变化。三轴高温高压试验系统是在实验室环境里模拟岩石深部环境，再现深部岩体的轴压、围压、地下水动力(水压渗流)和地热温度的物理条件，对岩石的综合物理力学性能进行研究而设计的一种机械系统[2]。电阻加热炉主要是利用电流通过热电阻丝或导电介质产生焦耳热能，根据电阻加热炉的加热对象的不同，在工业生产过程中又可以分为直接加热和间接加热两种形式[3]。由于间接加热不要求被加热物体为导体，故其适用范围相对较广[4]。目前大多数对液压与温度系统的控制一般使用传统PID控制器进行调节。传统PID控制器对于具有非线性、强干扰、不确定性特点的系统难以达到理想的控制效果[5-7]。PID的参数决定了PID控制器的控制效果。一般的 PID 参数整定方法过程较为复杂，在工作现场中常规方法往往因整定困难得不到非常有效的PID参数[8-10]。因此，PID参数整定问题愈发受到专家学者的重视。常规PID参数整定方法有ZN(Ziegler-Nicholes)[11-13]、CC(Cohen-Coon)方法[14]、内部模型控制(internal model control，IMC)[15-17].卢彬彬等[18]应用人工蜂群(ABC)算法实现了对航空发动机PID控制器的优化；顾冬华等[19]应用模糊神经网络控制方法，与无菌包装预热系统的PID控制器结合，实现了对PID参数的有效整定；宋娟[20]应用混合果蝇算法实现了对PID参数的寻优设计；谭冠政等[21]应用蚁群算法对智能人工腿PID控制器进行了优化设计。马丽楠等[22]提出IMC-PID控制器，建立滤波器参数与PID控制器参数之间的关系，解决了由于双闭环独立PID整定参数多且复杂的问题。随着具有非线性行为、高阶和长响应时间的工业系统复杂性的提升，进一步增加了PID参数设置的困难[23]。

吕红芳等[24]应用了基于免疫粒子群算法对PID参数进行优化，并证明了该算法的有效性；孙言锴等[25]应用了粒子群算法与模糊算法相结合的方法对PID参数进行了优化，解决了前驱体材料生产中反应釜中pH值控制。

粒子群算法对问题的维数相对敏感，将粒子群算法与其他算法相结合会因维数的增加而增加运算复杂度。本文为了确保试验机控制系统的稳定性提出了基于粒子群算法的PID参数优化方法。该方法相较于其他PID参数控制策略具有算法简单、搜索速度快、效率高等特点，使得试验机在试验过程中对外界环境及其岩石内部变化造成的干扰做出及时反应，并且迅速达到试验条件设定值后趋于稳定状态。

1 高温高压三轴试验机及控制系统数学模型

图1所示为高温高压三轴试验机。试验机由系统控制平台、高温三轴应力室、加热系统组成[26]。为了研究粒子群算法优化PID控制器对试验机控制系统的有效性，需要对试验机控制系统建立数学模型，得出试验机控制系统传递函数。文中对试验机控制系统均采用机理建模法。

图1 高温高压三轴试验机

1.1 液压控制系统及数学模型

高温高压三轴试验机液压控制系统图如图2所示，由油箱、液压泵、滤油器、电液伺服换向阀、电机、溢流阀、复合液压缸、压力传感器、控制器和伺服放大器等组成。

1-油箱；2-滤油器；3-电机；4-液压泵；5，9-电液伺服换向阀；6-溢流阀

假定阀和液压缸的连接管道对称且短粗，管道动态与管中压力损失可以忽略；液压缸各工作腔内各处压力相等，油温、体积弹性模量是常数；液压缸内、外泄漏均为层流流动[27]，可以得出：

电液伺服阀流量方程：

QL=kqxv-kcpL.

(1)

式中：QL为液压缸进油输入流量，m3/s；kq为伺服阀流量增益，L/(min·m)；xv为阀芯位移，m；kc为伺服阀的阀门压力，MPa；pL为供油压力，MPa.

液压缸流量方程：

(2)

式中：Ap为液压缸活塞有效工作面积，cm2；s为拉普拉斯变量；xp为液压缸活塞位移，m；Cip为液压缸总的泄露系数，L/(min·MPa)；Vt为系统总压缩体积系数；βe为液压油弹性模量，MPa.

液压缸力平衡方程：

Fg=Mts2xp+Bpsxp+Ksxp+FL.

(3)

式中：Mt为液压缸负载质量，kg；Bp为液压缸负载阻尼系数，(N·S)/mm；Ks为液压缸负载弹性刚度，N/m；FL为液压缸所受外干扰力，N.

综上(1)-(3)式可得出电液伺服阀控液压缸的传递函数Gp(s)：

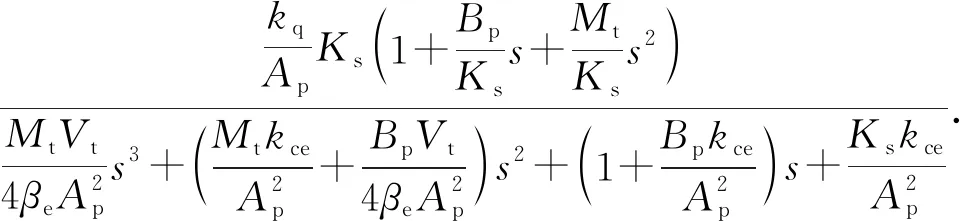
(4)

假设液压系统无弹性负载，负载仅为惯性负载，负载弹性刚度为0，负载阻尼系数Bp以及总流量压力系数kce很小，故忽略不计，且液压缸所受外干扰力与负载质量的作用相对比相差的数量级较大，对液压系统影响不大故忽略不计。因此(4)式可化简为：

(5)

电液伺服阀传递函数：

在动态特性分析中，电液伺服阀为二阶振荡环节。

(6)

式中：ωSV为电液伺服阀固有频率，Hz；KSV为电液伺服阀流量增益，L/(min·m)；ζSV为电液伺服阀阻尼比。

伺服放大器传递函数：

(7)

式中：I(s)为输出电流，A；U(s)为输入电压，V.

压力传感器传递函数：

(8)

式中：U(s)为输出电压，V；Fg2为液压缸的输出压力，N.

由(5)-(8)式可以得到高温高压三轴试验机的液压系统闭环传递函数框图见图3.

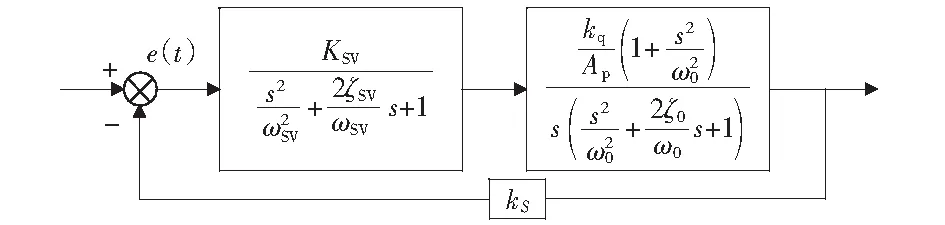
图3 液压系统闭环传递函数框图

1.2 温度控制系统及数学模型

通过分析电阻加热内部机理，得知其是一维的关系结构表达式。高温高压三轴试验机温控系统图如图4所示。

图4 高温高压三轴试验机温度控制系统

电阻加热内部温度与热量方程：

(9)

式中：Q为电阻丝加热的总热量，J；G为加热炉内控制重量，kg；Ca为空气的比热容；C为热容。

热能增量形式方程：

(10)

式中：R为热阻，Ω；ΔQ为热量增量，J；ΔTI为加热炉内的温度变化，℃；ΔTO为加热炉外的温度变化，℃.

对(10)式进行拉普拉斯变换得到：

(RCs+1)Tr(s)=RQ(s).

(11)

由式(9)-(11)得出电阻丝加热系统传递函数：

(12)

式中：K为放大系数，K=R；T为惯性时间常数，T=RC.

对试件进行加热时，电阻丝加热炉的温度不是循序渐进地增加，热传递过程有一个从输出到响应的延迟，存在一个渐变量。延迟的时间长短与加热的容积有关。因此，考虑到外部环境的干扰，电阻丝加热系统传递函数可改写为：

(13)

式中：τ为延迟时间常数。

温度传感器热电偶的传递函数：

(14)

由式(13)、(14)可以得出高温高压三轴试验机温度控制系统闭环传递函数框图见图5.

图5 温控系统闭环传递函数框图

2 粒子群算法优化PID

2.1 粒子群算法概述

粒子群优化算法是一种基于群体智能理论的算法，由Kennedy和Eberhart于1955年提出，源于鸟群捕食的行为，通过种群粒子间的合作与竞争产生群体智能优化搜索[28]。

通俗地讲，我们可以把粒子群想象为一群具有相互通讯的正在觅食的鸟群，然而每只鸟不清楚食物所在的具体位置，但是对于鸟类可以通过嗅觉判断食物与自己的距离以及判断自己在区域内的位置。鸟群中任意两只鸟可以清楚对方离食物的距离以及对方的位置。在此假设，每一只鸟飞行都会有惯性，并且每只鸟都会判断本身距离食物的距离和其它同类距离食物的距离以及它们的位置，然后选择下一次飞行的方向。最后，鸟群通过相互通讯，汇聚在食物的地点。食物的位置也就是我们在工业应用中产生的最优解。

为了求得最优解(鸟群向食物飞行)，粒子群算法(PSO)提出速度，以此来对粒子群更新，速度反映出鸟儿当前所在的位置距离事物的方向和位移，并且决定鸟儿飞行的方向及位移。速度值是通过个体极值以及全局极值来确定，个体极值就是单个粒子寻找到的最优解，全局极值就是粒子群寻找到的最优解，对应鸟儿自身的飞行目标和同伴的飞行目标，凭借这两点，鸟儿找到食物所在的位置及粒子群找到最优解。

vt+1=wvt+c1r1(Pt-xt)+c2r2(Gt-xt) .

(15)

xt+1=xt+vt+1.

(16)

式中：v表示粒子速度；x表示粒子的位置；w为惯性权重；c1、c2为加速度常数；r1、r2为[0,1]之间的随机数；Pt是粒子当前寻找的最优位置；Gt是整个粒子群当前寻找的最优位置。

2.2 PID控制器

目前，工业上使用的控制器大多采用PID控制器，根据输出值与给定值的差e(t)通过下列数学公式计算来控制输出。

(17)

式中：Kp为比例系数；Ki为积分系数；Kd为微分系数。

PID控制器的灵敏度也是由这3个参数来确定的，但对于这3个参数通过人为的确定效果并不是很好，并没有达到控制系统快速响应、稳定运行的状态。

2.3 粒子群算法优化PID参数

利用粒子群算法(PSO)分别对温度控制系统PID控制器的参数Kp、Ki、Kd，液压(轴压)控制系统PID控制器的参数Kp、Ki、Kd和液压(围压)控制系统PID控制器的参数Kp、Ki、Kd，进行整定。选择PID控制器中的Kp、Ki、Kd作为粒子群算法(PSO)的粒子，最终的参数优化目标是粒子速度趋于零。粒子群算法(PSO)优化PID参数的流程图，如图6.

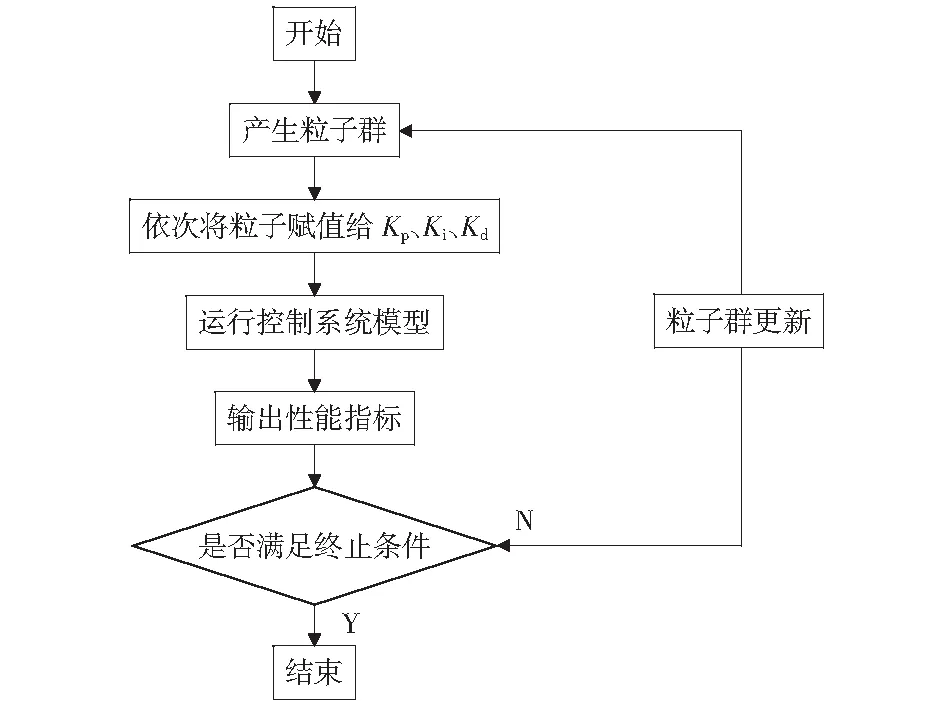
图6 粒子群算法(PSO)优化PID参数流程图

粒子群算法优化PID参数过程：

1) 初始化。粒子群算法(PSO)中的参数，最大迭代次数100次，粒子群规模为100，c1、c2加速度常数为2，惯性权重w=4以及粒子空间搜索范围。

2) 粒子群随机产生每一个粒子的速度和位置，通过适应度函数J计算每一个粒子的适应值，确定Pt和Gt.适应度函数J如下：

(18)

3) 通过公式(15)和(16)更新粒子的速度与位置，计算新粒子的适应度，更新粒子最优的Pt和Gt.如果粒子达到预设的迭代次数和适应度下限值，则得出参数最优解结束算法，反之返回步骤2).

2.4 基于粒子群算法的高温高压三轴试验机控制系统PID控制器结构

试验机控制系统进行轴压控制时，首先将轴压信号输入到PID控制算法中，得到轴压控制输出，计算轴压的控制误差，粒子群算法通过轴压控制误差反馈对PID控制参数进行调整，使轴压控制误差尽可能减小，提高轴压的控制精度，控制结构图如图7所示。

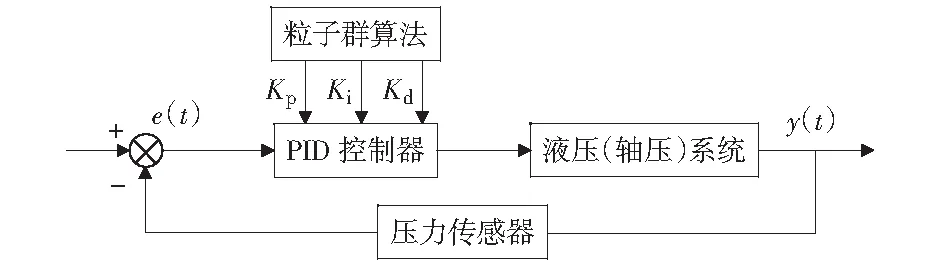
图7 轴压控制系统结构图

围压控制原理如图8所示。首先将围压信号输入到PID控制算法中，得到围压控制输出，计算围压的控制误差，粒子群算法通过围压控制误差反馈对PID控制参数进行调整，使围压控制误差尽可能减小，提高围压的控制精度。

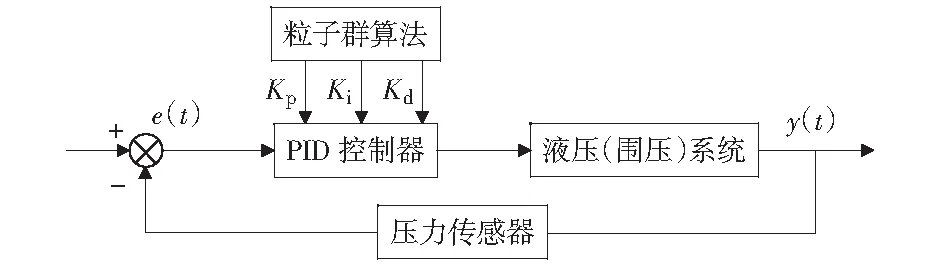
图8 围压控制系统结构图

温度控制原理如图9所示。首先将温度信号输入到PID控制算法中，得到温度控制输出，计算温度的控制误差，粒子群算法通过温度控制误差反馈对PID控制参数进行调整，使温度控制误差尽可能减小，提高温度的控制精度。

图9 温控系统结构图

3 仿真实验分析

液压系统在Simulink仿真过程中的参数：液压油弹性模量Ee=700 MPa；液压缸负载阻尼系数Bp=9 (N·S)/mm；液压缸活塞有效工作面积(轴压)Ap=0.20 dm2；液压缸活塞有效工作面积(围压)Ap=0.59 dm2；液压缸总的泄露系数Cip=1.3 L/(min·MPa)；伺服阀的阀门压力kc=14 MPa；伺服阀流量增益kq=2 L/(min·m)；液压缸负载质量Mt=20 kg；系统总压缩体积系数Vt=7.16 dm3.温控系统在Simulink仿真过程中的参数：K=8；T=3 360；τ=60.

分别利用传统PID控制器和模糊PID控制器，粒子群算法优化PID控制器对试验机的温度压力进行控制，通过仿真研究得到系统的阶跃响应见图10、图11和图12.