PDMS基磁性复合薄膜制备及其非线性力磁耦合研究

葛 阳，谭秋芸，姜交林，吴凯乐，桑胜波

(太原理工大学 信息与计算机学院，微纳传感与人工智能感知山西省重点实验室，太原 030024)

随着传感器小型化、集成化、智能化的发展趋势，结构形式灵活多样、可根据测量要求任意布置的柔性传感器成为特殊环境下实现小信号精确、快速识别的重要方式之一，尤其在生物传感技术、电子皮肤触觉以及可穿戴技术领域市场前景广阔[1-3]，发展状态可逆且快速响应的基于智能复合材料的高性能柔性传感器的需求不断增加[4-5]。近年来，智能复合材料在宏观力学、电学以及光学方面受到研究学者的广泛关注[6-7]。

作为新型纳米复合材料之一的磁流变弹性体，已被应用于变刚度器件[8-9]，其在保留原有聚合物刚性的基础上，材料的模量、刚度、阻尼可快速可逆地响应外界磁场变化[10-13]，还可克服磁流变流体(如磁流体)所面临的如铁颗粒沉积、密封与环境污染等问题[14-16]。与传统的磁流变弹性体基体材料如天然橡胶、硅橡胶等相比，聚二甲基硅氧烷(PDMS)高分子聚合物材料具有良好的生物相容性和极宽的温度稳定性、光学透明性以及稳定的物理化学特性，成为柔性传感器中构建磁流变弹性基体的重要候选材料之一[17-19]。

磁场诱导自组装是实现PDMS基磁性复合薄膜磁有序结构的有效手段。近几年，已有研究报道利用磁场诱导自组装方法制备出具有磁、光以及力学性能的各向异性材料[20]。然而，纳米颗粒的磁化是一个极其复杂的过程，晶粒大小和取向、机械加工条件及外部温度等因素都会对材料的磁响应特性产生重要影响[21-22]。磁性复合薄膜在磁场环境下还会产生复杂的非线性磁致力学行为。如何基于磁纳米颗粒，制备出具有高磁致传感效应的PDMS基磁性复合薄膜，成为柔性电子传感领域亟待解决的关键问题之一。

本文采用PDMS作为磁性复合薄膜的磁流变基体材料，采用四氧化三铁(Fe3O4)作为磁纳米颗粒，在磁场环境下制备出可以响应外界磁场强度的微米级PDMS基磁性复合薄膜，并对其铁磁性与非线性磁致力学行为进行了测试与分析。此外，本文还通过有限元仿真，构建出具有磁致形变效应的高灵敏传感模型，挖掘了PDMS基磁性复合薄膜的非线性力磁耦合特性，表明其在状态可逆且响应迅速的高灵敏柔性传感器研究中的潜在应用价值。

1 实验制备方法

1.1 实验材料

实验用到的材料有：用于制备磁性复合薄膜的Fe3O4纳米颗粒(CAS号1317-61-9)；用于制备PDMS的预聚物与固化剂。

1.2 制备仪器

制备PDMS基磁性复合薄膜所用仪器包括电子天平、搅拌脱泡机(KK-300SS)、匀胶机(型号EZ4)、可调温加热平台(型号V-1515)、数控电磁铁磁场发生系统(型号CH-WD50)。

1.3 制备方法

图1为PDMS基磁性复合薄膜的制备流程示意图，具体制备步骤如下：

图1 PDMS基磁性复合薄膜制备流程示意图

1) 配置混合溶液。首先将不同含量的Fe3O4纳米颗粒(质量分数分别为5%、10%、20%)和PDMS预聚物在室温下初步搅拌，将溶液置于搅拌脱泡机中以2 000 r/min的转速充分搅拌30 min.

2) 添加固化剂。固化剂与PDMS预聚物质量比为1∶10.

3) 旋涂制备PDMS基磁性复合薄膜。以玻璃片作为基底，旋涂配置好的混合液。在匀胶机中旋涂转速为1 000 r/min，时间为90 s.PDMS基薄膜初步成型。

4) 磁场诱导。将初步成型的薄膜放入数控电磁铁磁场发生系统的磁场中，在磁场诱导下改变薄膜中纳米颗粒的分布，沿磁场方向形成链状结构。

5) 加热固化。将样品置于加热台加热10 min，温度为120 ℃.

6) 脱膜。待加热固化的薄膜冷却后，泡入稀硝酸15 min后取出，即可获得PDMS基磁性复合薄膜。

2 结果与讨论

2.1 样品形貌及成分表征

使用数字显微镜(Olympus DXS1000)对所制备的PDMS基磁性复合薄膜(Fe3O4质量分数为10%)形貌进行了观察与分析，如图2(a-c)所示。在零磁场条件下制备PDMS-Fe3O4磁性复合薄膜，磁性颗粒呈均匀分布，复合薄膜表现为面内各向同性(图2(a)).在外加磁场条件下，可制备出具有面内磁各向异性的PDMS-Fe3O4磁性复合薄膜：预结构磁场沿薄膜平面方向，薄膜表现为平行各向异性(图2(b))；预结构磁场沿薄膜厚度方向，薄膜表现为垂直各向异性(图2(c)).进行了样品成分XRD表征，如图2(d)，磁性复合薄膜主要由Fe3O4晶相组成。此外，通过台阶仪测量了磁性复合薄膜的厚度，其中，旋涂机转速为300 r/min时所制备薄膜厚度为312.27 μm，转速为500 r/min和1 000 r/min时所制备薄膜厚度分别为130.23 μm、48.15 μm.

(a)磁各向同性；(b)平行磁各向异性；(c)垂直磁各向异性；(d)Fe3O4 XRD图谱

2.2 PDMS基磁性复合薄膜铁磁性研究

我们研究了室温下PDMS-Fe3O4磁性复合薄膜磁各向异性与各向同性对PDMS基磁性复合薄膜磁学性能的影响。图3(a)为所制备样品的磁滞回线对比图。从图3(a)中插图可以看出，当Fe3O4质量分数都为10%时，磁各向同性PDMS-Fe3O4磁性复合薄膜剩余磁化强度约为0.3 emu/g，而垂直、平行各向异性PDMS-Fe3O4磁性复合薄膜剩余磁化强度分别约为0.5 emu/g和1.05 emu/g，即平行各向异性PDMS-Fe3O4磁性复合薄膜是同条件下无磁场诱导制备的各向同性磁性复合薄膜剩余磁化强度的2.5倍。磁场诱导下制备的各向异性PDMS-Fe3O4磁性复合薄膜比各向同性磁性复合薄膜具有更好的铁磁性能。

其次，研究了室温下磁性颗粒浓度对PDMS基磁性材料复合薄膜磁学性能的影响。对比5%、10%、20%三个不同Fe3O4颗粒质量分数的磁性复合薄膜，如图3(b)及其插图，饱和磁化强度分别为1.7、2.1和3.9 emu/g，剩磁分别约为0.17、0.25和0.4 emu/g.磁性颗粒浓度较高的复合薄膜更易于磁化，铁磁性更强。此外，在垂直磁场下，不同厚度的磁性复合薄膜剩余磁化强度相差较大。300 μm厚度的磁性复合薄膜其剩余磁化强度可达1.06 emu/g，比50 μm厚度磁性复合薄膜的0.43 emu/g高一倍，如图3(c)插图。不同厚度下磁性复合薄膜饱和磁化强度无显著差别，约5.7 emu/g。相同质量分数，磁性复合薄膜厚度越大，薄膜中所含磁性纳米颗粒越多，受磁场作用力越大，复合薄膜中剩磁更多。

(a)10%质量分数下磁各向同性与面内磁各向异性对比；(b)20%、10%、5%磁各向同性复合薄膜磁滞回线对比；(c)不同厚度的面内磁各向异性薄膜对比；(d)20%、5%面内磁各向异性薄膜热磁曲线

除了磁场环境、薄膜厚度和浓度，温度也会对磁性复合薄膜的磁化状态造成较大影响。热磁曲线测试(如图3(d))显示，当温度由200 K升至350 K时，Fe3O4质量分数20%的各向异性磁性复合薄膜磁化强度从3.65 emu/g降到3.38 emu/g，Fe3O4质量分数5%的各向异性磁性复合薄膜磁化强度从1.82 emu/g降到1.71 emu/g，即不同Fe3O4质量分数的磁性材料复合薄膜在低温下磁学性能表现更佳。

2.3 PDMS基磁性复合薄膜磁流变测试与分析

为了证明PDMS基磁性复合薄膜磁流变效应，本节详细研究了磁结构分布对复合薄膜应力变化和磁致形变的影响。首先，在上述制备出的不同磁结构分布的PDMS-Fe3O4磁性复合薄膜基础上，测试并计算出样品的应力与磁致形变，如图4所示。由图4(a)，通过万能材料试验机在0～0.2应变范围内测量磁性复合薄膜的应力，薄膜拉伸应力与应变表现出正线性相关。在应变为0.195时，磁各向同性复合薄膜拉伸应力达到0.218 MPa，大于面内磁各向异性复合薄膜的拉伸应力(0.18 MPa与0.14 MPa).由此，磁场诱导制备薄膜时，Fe3O4纳米颗粒在外加磁场下可自组装成链条结构，粒子间相互作用增强，导致磁性复合薄膜相同拉伸应力下的应变量增大。

接着研究了PDMS基复合薄膜磁致形变效应以及磁结构分布与厚度对磁致形变的影响。利用数控线圈磁场发生系统自主搭建了薄膜磁致形变测量平台。如图4(b)，对PDMS-Fe3O4磁性复合薄膜施加垂直磁场，复合薄膜产生了磁致形变效应，即PDMS基磁性复合薄膜可有效响应磁场变化。由图4(c)，磁性复合薄膜的形变随磁场增大而增大，在50 mT后形变量趋于饱和。与各向同性PDMS-Fe3O4磁性复合薄膜相比，经过磁诱导制备的各向异性复合薄膜磁致形变灵敏度更高，在H=60 mT时可达到最大偏转角，约80°。对于平行各向异性复合薄膜，外磁场垂直于薄膜内部磁链方向，将引起更大的磁相互作用力，因此平行各向异性PDMS-Fe3O4磁性复合薄膜的形变大于垂直各向异性复合薄膜。如图4(d)可知，H=80 mT时，50 μm厚度复合薄膜形变角度高达79°，厚度为300 μm时形变角度仅达67°.因此，在相同的铁磁条件下，薄膜厚度越小，磁致形变效应越强。综上，通过磁诱导，PDMS基磁性复合薄膜在相同应力下应变量、磁致形变量得到提高。

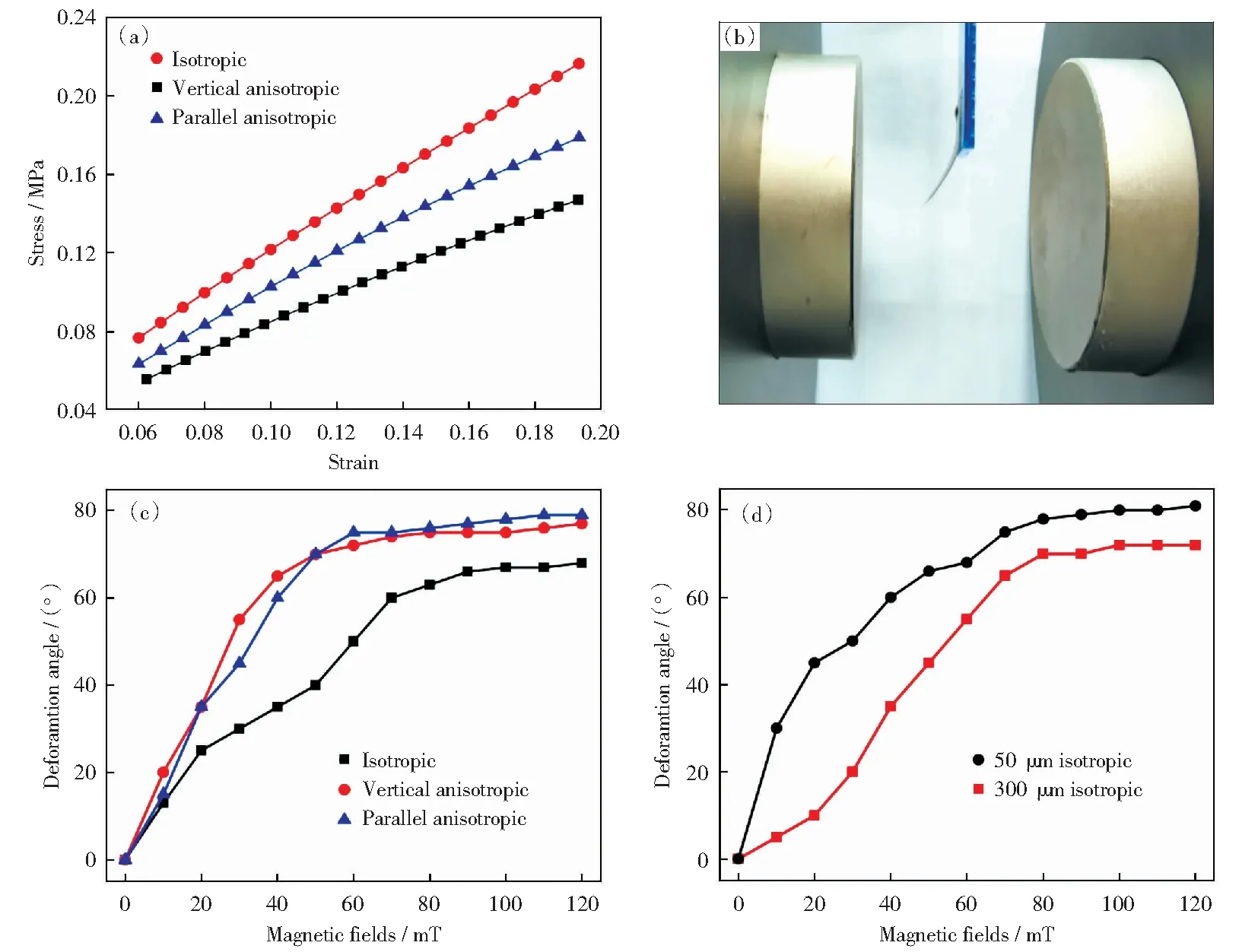
(a)应力-应变图；(b)薄膜磁致形变测量平台；(c)磁结构分布对磁致形变量的影响；(d)厚度对磁致形变量的影响

2.4 PDMS基磁性复合薄膜非线性力磁耦合理论分析

基于磁偶极子微观模型可得到复合薄膜磁致应力-应变关系，开展对PDMS基磁性复合薄膜非线性力磁性质的研究。根据Rosenzweig理论，颗粒间的磁能可以通过点偶极子m1和m2之间的相互作用能表示为：

(1)

式中：μ1是聚合物基体的相对磁导率；μ0是真空磁导率；er是两个球形粒子形成的点偶极中心线的单位向量；m1和m2表示粒子的磁偶极矩大小；r表示两个磁偶极子之间的距离；m=mi·er表示磁矩矢量。θ是磁矩方向与磁链方向之间的夹角，满足以下的形式：

(2)

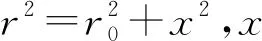
(3)

磁性粒子的总数为：

(4)

其中，铁磁粒子的体积为Vi，磁性复合薄膜的体积为Ve，磁性复合薄膜中铁磁性的含量(体积分数)为φ，d为颗粒直径。由此，我们可得到每单位体积的相互作用能量密度：

(5)

通过对公式(5)粒子间相互作用能量密度取微分，可以得到磁流变复合薄膜的剪切应力。因此，应力-应变本构方程可以被描述为：

(6)

2.5 PDMS基磁性复合薄膜“力-磁”耦合仿真分析

为了验证并挖掘PDMS基复合薄膜的非线性“力-磁”共形耦合机制，本节通过有限元分析法，基于Comsol Multiphysics中的AC/DC和固体力学模块，搭建了PDMS基磁性复合薄膜模型，分析结果如图5所示。图5中，磁场被垂直施加到PDMS-Fe3O4磁性复合膜上，此时，各向同性磁性复合薄膜所受应力不均匀(图5(a))，应力最高可达0.6 kPa，而各向异性复合薄膜中心处所受应力最大(图5(b))，高达5 kPa.接下来，对各向同性和各向异性的复合薄膜的磁致形变效应进行了模拟，当磁场强度为30 mT时，各向同性与各向异性复合薄膜位移分布差异显著，即各向同性复合薄膜位移分布不规则(图5(d))，且最大位移仅达3.8 μm，而各向异性最大位移发生在PDMS-Fe3O4磁性薄膜中心(图5(e))，最大偏移约为58 μm.因此，相同质量分数下，各向异性的PDMS基磁性复合薄膜可产生出较大的饱和磁化强度和剩余磁化强度，这是导致更大应力值和磁致形变量的主要因素，也是PDMS基磁性复合薄膜产生非线性“力-磁”耦合效应的内在作用机制。

(a)各向同性应力分布图；(b)各向异性应力分布图；(c)各向同性位移分布图；(d)各向异性位移分布图；(e)浓度对磁致形变的影响；(f)磁场强度对应力与形变的影响

此外，我们研究了Fe3O4颗粒质量分数对各向同性与各向异性PDMS基磁性复合薄膜偏移响应的影响。如图5(e)所示，在相同的磁强度下(30 mT)，对比3%、6%、10%三种质量分数的磁致形变，随着浓度增大，复合薄膜偏移量增大，各向异性复合薄膜表现出比各向同性复合薄膜更大的偏移。质量分数为4%时，磁场强度从100 mT提高到500 mT，偏移量从0.8 μm提高到2.5 μm(图5(f))，即外磁场强度可显著增大PDMS-Fe3O4磁性复合薄膜的形变。由磁流变本构关系(公式6)，PDMS-Fe3O4磁性复合薄膜的磁致应力与磁场呈非线性相关。当磁颗粒磁矩方向与外磁场一致后，磁性复合薄膜的磁化强度逐渐达到饱和，即300 mT为最优变形磁场。为了验证这种解释，我们进一步仿真了各向异性PDMS-Fe3O4磁性复合薄膜在100 mT到500 mT磁场强度下的应力特性，结果如图5(f)点线图所示，薄膜的应力随着外磁场强度的增大而显著增加，从0.9 kPa增加到2.8 kPa，但当磁场达到400 mT之后，磁致应力逐渐趋于饱和。

最后，我们对比了不同磁纳米颗粒TbDyFe、Fe-Ga、Fe-Co磁性复合薄膜的磁流变效应，构建了不同材料的磁各向同性与各向异性磁性复合薄膜模型，如图6所示。与上述铁磁性研究一致，同种材料下，各向异性PDMS基磁性复合薄膜剩余磁化强度更高，磁性颗粒质量分数相同的各向异性PDMS基磁性复合薄膜表现出比各向同性复合薄膜更大的应力。如图6所示，PDMS-TbDyFe、PDMS-Fe-Ga、PDMS-Fe-Co磁各向异性复合薄膜中，由于TbDyFe饱和磁致伸缩系数高达1 005×10-6，因此TbDyFe磁化强度最高，故PDMS-TbDyFe磁性复合薄膜应力最大(图中红色显示出最大应力，达30 Pa)，而具有最小饱和磁致伸缩系数(78×10-6)的Fe-Co磁纳米颗粒其磁性复合薄膜应力最小(图6中蓝紫色显示出最大应力，达10 Pa)，该结果与上述分析的磁流变本构关系理论一致。

图6 不同磁纳米颗粒PDMS基磁各向同性(a)和各向异性(b)复合薄膜的磁流变效应对比

3 结论

本文采用磁场诱导生长方法，基于Fe3O4磁纳米颗粒，制备出状态可逆且快速响应磁信号的PDMS基柔性复合微薄膜。使用数字显微镜表征了样品形貌，采用XRD表征了样品晶相，通过VSM测量了样品的磁滞回线，通过数控电磁铁磁场发生系统测量了样品的磁致应力行为。测试结果表明，在磁场诱导下，PDMS基磁性复合薄膜可展现出面内磁各向异性与磁致应变行为。最后，通过有限元分析法从理论上验证并挖掘了复合薄膜的非线性“力-磁”共形耦合机制，为PDMS基磁性复合薄膜磁致应力特性提供了重要的理论支撑。