中学数学解题中联想思维法的应用

尹 含*

（淮阴师范学院数学与统计学院，江苏 淮安 223001）

0 前言

数学题目具有逻辑性与复杂性，通常是多方面知识点的融合，重点考查其中若干知识点。在解答中学题目时，不仅需要充分掌握基础知识，而且应对知识进行体系化联想记忆和应用，形成解题直觉，从而在实际解答问题时产生灵感，降低解题难度，逐步提升解题能力。传统学习方法对数学联想思维的重视度不足，在解题时思维灵活性较差。为此，应积极应用联想思维法解题，获得解题新思路。

1 联想思维法

联想思维法是指在处理问题时利用联想思维对问题进行解构和分析，从而辅助解题者得出清晰的解题思路，最终获得正确答案。联想是重要的思维能力，大脑在对一件事物进行感知时，受其经验、记忆和知识结构等影响，可能回忆起与该事务具有相关性的其他事务，这一思想过程即为联想。解答数学问题需要构建数学思维，通过联想应用已知知识分析未知问题，促使数学知识与数学题中待解决对象之间构建一定联系。在认识事物时，思维将对事物内在联系进行分析和认知，实现由此及彼的思维过程。该思维活动过程中，联想思维具有纽带作用。在解答未知问题时，需要利用已知知识、逻辑、方法等对问题进行剖析，从而解决未知问题。在解答数学问题时，需要从已知条件出发，分析其中隐含的图形特征等，进行相关知识联想，分析解题思路。在此过程中，联想思维法具有显著的应用价值[1]。

联想思维使用的基础是具有一定数学知识基础，应用该方法有利于解决数学问题。通过联想可促进知识有效记忆，调动已有的知识记忆，同时在不同方法之间构建科学联系，从而构建系统性知识网络。通过联想可对思维活性进行训练和激发，从题中信息出发，进行合理联想，调动知识基础然后形成解题思路，对于提升解题能力具有重要意义。联想思维应用有利于培养和增强学习兴趣，促进长效学习，同时有利于深入理解知识，拓展学习方法，提高解题效率。

2 中学数学解题中联想思维法的应用功能与原则

2.1 应用功能

知识功能是联想思维应用的基础功能。获取题目信息后，以问题为切入点进行题目解构，分析其中涉及的定义、定律或定理等知识点，综合分析基础知识，形成基本认知。提出问题后，从题目本身为出发点进行新知识学习。通过使用联想思维分析数学问题，从此问题延伸至同类其他问题，在不断解答问题过程中完善思维模式，拓展联想空间，总结解题经验，最终得出结论。在此过程中，应自觉构建知识体系，然后将联想思维法纳入该体系中，充分练习提高应用熟练度，完善知识结构。该功能有利于从宏观层面理解和掌握知识。

2.1.2 教育

在解题过程中，大脑进行思维活动，在此过程中思维能力不断提升。想要应用联想思维解决实际问题，必须思维方向明确，具有明确的解题目的性，在解题活动中对题目包含的丰富信息进行辨别，提升联想思维能力，实现教育功能。

2.1.3 评价

在解题训练中，需要对学习效果进行评价。针对单元学习情况进行检测，通过自我检测客观评价实际学习成效。联想思维应用中，需要调动已知知识，在联想活动中可对自身知识掌握情况进行自检，针对性加强学习，构建完善的知识体系。

2.2 应用原则

2.2.1 科学性

在采用联想思维解答数学问题时，应坚持科学性原则，合理制定联想思维训练计划，明确应用思路。在联想思维能力训练中，不仅需要进行解题训练，而且应进行数学题编写思路分析，逆向推理出题人意图，明确考查知识点，从而构建更科学的解题方法。利用已知知识分析题目时，应从题目的逻辑性出发，鼓励拓展思维，但是在解题时应避免“剑走偏锋”，需要围绕主线知识进行思考和解答。

由图2可知，不管是无改性活性炭，还是30%HNO3改性活性炭，DBP的去除率都随着活性炭投加量的增加而增加。当无改性活性炭投加量达到0.12g时，DBP去除率达到56%，而30%HNO3改性活性炭投加量在0.12g时，略低于无改性活性炭，DBP去除率为49%。

2.2.2 严谨性

在构建联想思维时，应坚持思维严谨性，根据自身学习进度和实际解答能力为基础进行难度适度的解题训练，循序渐进地夯实基础知识，逐步提高解题难度。应在充分掌握一种解题方法后，再进入下一循环知识学习。在解题训练中应坚持量力而行，避免急于求成，保证知识框架严谨、完善。

2.2.3 目的性

联想思维训练和应用应具有明确目的，在不同学习阶段设定相应学习目标，然后根据阶段性学习目标科学设计学习方法，进行专项解题训练。在解题训练中，应针对不同难度的题目进行训练，从而保证良好的训练结果。

3 中学数学解题中联想思维法的应用方法

3.1 从表到里

数学解题方法具有一定逻辑性，即使是难度较高的数学题也需要以基础知识构建而成。数学学习框架虽然具有系统性特点，但是实际知识比较零散，在解题时要求解答者科学应用基础知识和表面知识，策略性发现解题关键，得出可行性解题思路。

3.2 从难到易

在联想思维使用中，应采用循序渐进的学习方法，初期解决难度较低的问题，持续提升解题难度，有意识地训练联想思维，联想思维应用熟练后，可促使难题解答变得简单。例如，在几何题解答中，根据定义，两点间的距离公式为[3]：

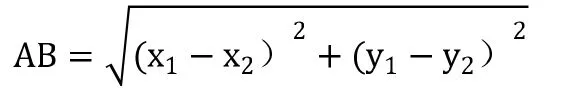
从上述关系式进行联想，进而想到含根式函数问题。例如：现 x 轴上有两个定点，分别为 A（3，2）与 B（-1，-4），另外有有一动点，描述为p（x，0），p点至A点和B点的距离之和应描述为：

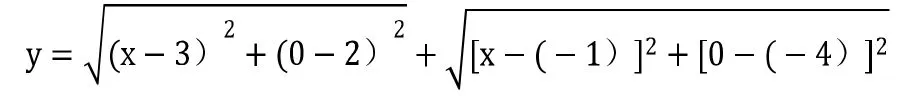
3.3 从阻到通

通过科学运用联想思维，可疏通数学解题关卡，促进问题轻松解答。直觉思维是数学学习中的重要思维，也是科学研究必备素质。为促进灵感激发，应积极培养直觉思维。全方位分析问题，无需详细思考具体思维过程，而是利用直觉思维触及问题本质，形成预感性判断。灵感是联想发生的诱因。在面对各种数学问题时，许多问题涉及多方面因素，难以迅速厘清解题思路，在解答时感觉无从下手。此时有效使用联想思维激发解题灵感，探索解题新思路。通过此种方法，有利于降低解题难度，消灭数学学习过程中的“拦路虎”。例如，在关系式中[4]：

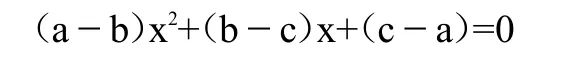
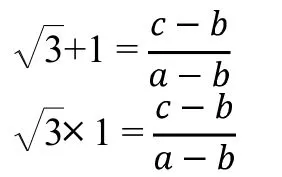
从上述关系式可得出如下关系式：

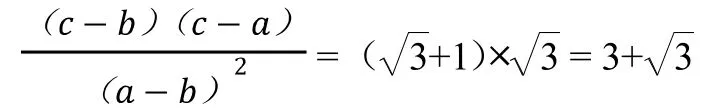
从而使问题得到解答。该题解答中重点是进行知识联想。

3.4 充分拓展思维空间

在数学解题中应做到由此及彼，积极拓展和训练联想思维。相关研究认为，通过逐步构建联想思维可形成直觉，直觉成熟和积累后形成猜想。从外界获取的信息经过大脑加工，无数孤立或零散的信息被重组，构建一定联系，经过此种处理后大脑从中可获取新的信息。此种信息重组过程和最终成效受到个人联想空间开阔性的直接影响。在面对数学问题时应自觉调动联想思维[5]。

例如，在函数问题解答中，已知f（x）定义域是R，a为非0常数，并且符合x，y∈R条件。此外，f（x）符合下列关系式：

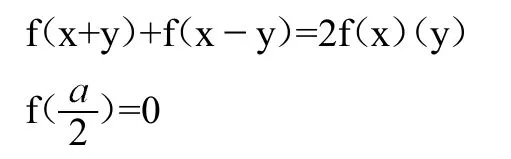
利用以上已知条件，试解答f（x）是否为周期函数。

在解答此题过程中，可从该等式结构特征联想到三角不等式，进而进行深入联想，得出 cos（x+y）+cos（x y）=2cosx cosy。f（x）与具有相似性，由此联想，然后为。在上述联想信息中，a与相似，f（x）的周期是2a，因此得出f（x）属于函数。通过上述联想过程形成直觉，利用数学直觉解决数学难题，实现学习突破。因此在日常学习中不仅应重视数学知识的融合应用，而且应重视思维训练的重要性，积极训练联想思维，

3.5 不断进行自我启发

在数学学习中应充分利用互联网资源，积极了解最新学习方法，自觉培养自身学习兴趣，联合数学基础知识构建生动的解题情境、科学设置问题，训练创新思维、联想思维和发散性思维等。在解题时不仅追求得出题目答案，而且应主动进行思考，力求由此及彼、举一反三，拓展思维方向，促进多维度思考，自觉完成从知识认知到思维方法构建的过程，通过科学掌握学习方法构建多元化解题思路，提高自身学习效率。在日常数学学习和解题训练中，应积极思考和进行辩证思维学习，增强独立学习能力，同时积极构建长效学习模式，形成良好的学习习惯，从细微知识点着眼，持续进行自我启发。

在解题中采用多元化思考模式，主动构建系统性数学知识框架，并且持续对知识框架进行填充和完善。在同一题目中，应适当融入多样化知识点，构建多元化解题模式，努力得出逻辑清晰的个性化解题思路，促进多元化解题方法应用，应用创新方法解答问题。在解答数学问题过程中，应努力突破思维局限性，采用多种方法解答问题，同时注重总结解题方法论。在解题训练中应从基础知识出发，同时有计划地拓展知识面，加强解题训练，探索更多可能性解题方法，拓展思维宽度，进行创新探索。及时总结自身创新性思考，保持自主思考积极性，自觉培养发散性思维。通过多元化学习增强全方位解题能力。

通过解题实践可知，在解题中应用联想思维效果显著。联想思维可辅助解题者构建科学的解题思路，从复杂的题目信息和知识点中定位核心知识点，厘清解题思路，形成解题灵感，充分利用思维直觉。此种方法适用于具有一定难度的数学题，可增强思维灵活性，改善思维能力，提高解决数学难题的能力。数学是知识构成复杂的学科，同时不同知识点之间存在一定联系，具有逻辑性。培养数学能力过程中既要培养有意识的解题能力，同时也应积极培养潜意识能力，即联想思维等能力。

4 结论

综上所述，联想思维法在数学问题解答中具有显著的应用价值，通过应用此种方法可有效构建解题思路，降低解题难度，辅助解题者构建清晰的解题思路，同时完善知识体系。在应用该方法时应从其特点出发，严谨、科学、目的明确地应用该方法，促进有效解决问题。在此过程中应积极总结方法论，加强思维训练，提升学习能动性，为学生数学能力的提升提供保证，促使学生数学学习效果得到改善。