基于遗传算法的反应堆三维屏蔽结构高维多目标优化方法研究

张华健 陈珍平 刘程伟 杨 超 谭 波 甘 斌 陈富财 于 涛

1（南华大学核科学技术学院 衡阳 421001）

2（中国核动力研究设计院核反应堆系统设计技术国家重点实验室 成都 610213）

3（湖南省数字化反应堆工程技术研究中心 衡阳 421001）

辐射屏蔽结构设计是反应堆设计的重要组成，是保障反应堆安全性与经济性的重要环节。随着核反应堆应用领域的日渐广泛（如船舶、航空、勘探与紧急救援等）及先进核反应堆设计的不断探索，核反应堆屏蔽结构设计面临高要求、无经验、难取舍等多种难题。

传统屏蔽结构设计主要依赖专家经验，辅以确定论方法或蒙特卡罗方法，进行多轮次迭代修正［1］。近年来，有学者基于最优化理论和算法研究新的辐射屏蔽结构设计方法，在单优化目标的屏蔽设计问题上具有良好表现［2-4］。因此，国内外开展了一系列优化算法研究，以实现屏蔽结构设计方案自动寻优。目前，单目标优化研究已拓宽至多目标优化领域，能较好解决2～3目标的反应堆屏蔽优化设计问题［5-7］。

然而，实际工程中三维屏蔽结构设计过程复杂，待优化目标远超3个，属于高维多目标优化问题（大于等于4个以上待优化目标的问题）范畴，传统优化方法已无法完全满足工程设计需求。因此，为进一步扩宽基于优化算法理念的屏蔽设计优化方法的应用范围，本文基于第三代非支配排序遗传算法（Non-dominated Sorting Genetic AlgorithmⅢ，NSGA-Ⅲ）［8］面向三维屏蔽结构开展高维多目标优化方法研究。

1 高维多目标优化问题

辐射屏蔽设计通常需要对重量、体积、辐射剂量率分区等多个设计目标进行综合考量，其中任意一个设计目标的优化还往往会导致其他一个或多个设计目标的劣化，是一个典型的高维多目标优化问题。

基于传统进化多目标遗传算法的屏蔽结构多目标优化方法在求解二维或三维的屏蔽结构优化问题上具有良好效果。但当待优化目标维度增至高维（大于等于4）多目标时，其求解过程主要面临以下两个问题［9］：其一，种群中非支配个体占比随目标维度增加呈指数形式增加，空间搜索能力退化难以收敛；其二，高维多目标问题下，拥挤度算子［10］计算复杂，且不适合评价种群多样性。因此，研究适用于三维屏蔽结构的高维多目标优化方法，具有一定工程意义。

文中三维屏蔽结构高维多目标优化问题的数学模型可表示为：

式中：X为n维决策向量X=(x1，x2，…，xn)，包含各屏蔽层厚度、材料等信息；W(X)为屏蔽层总重量；V(X)为屏蔽层总体积；RAU(X)为屏蔽层外围轴向上方辐射剂量率；RAL(X)为屏蔽层外围轴向下方辐射剂量率；RR(X)为屏蔽层外围径向辐射剂量率；Tmin为屏蔽层单层最小厚度；Tmax为屏蔽层单层最大厚度；Mmin为可选屏蔽材料最小序号；Mmax为可选屏蔽材料最大序号。优化目标为寻找一组X*=使F(X*)在兼顾5个优化目标的情况下达到较优结果。

2 基于NSGA-III高维多目标优化方法

本文主要基于NSGA-III算法建立三维屏蔽结构多目标优化方法。基本思想：将若干屏蔽结构设计方案的集合作为生物种群，每个方案以特定编码后的染色体（一组二进制数）进行表征，染色体内基因片段代表对应方案的设计参数，如材料类型、屏蔽层厚度和布置位置等，基于“优胜劣汰，适者生存”的自然进化法则，以设计方案的屏蔽层重量、体积和分区的辐射剂量率作为适应度考量标准，指导方案寻优。

三维屏蔽结构优化设计方法流程图见图1。其主要由构建屏蔽结构方案初始解空间、方案适应度值计算、方案性能评价方法、新方案生成操作和方案集合选择策略5个关键步骤组成。

图1 三维屏蔽结构优化设计方法Fig.1 Flow chart of the 3D shielding structure optimization design method

2.1 构建屏蔽结构方案初始解空间

基于待优化三维屏蔽结构模型（图2），提取屏蔽结构信息（表1），并将三维屏蔽结构设计优化问题，转换为特定空间几何上各材料与屏蔽层厚度的组合优化问题。

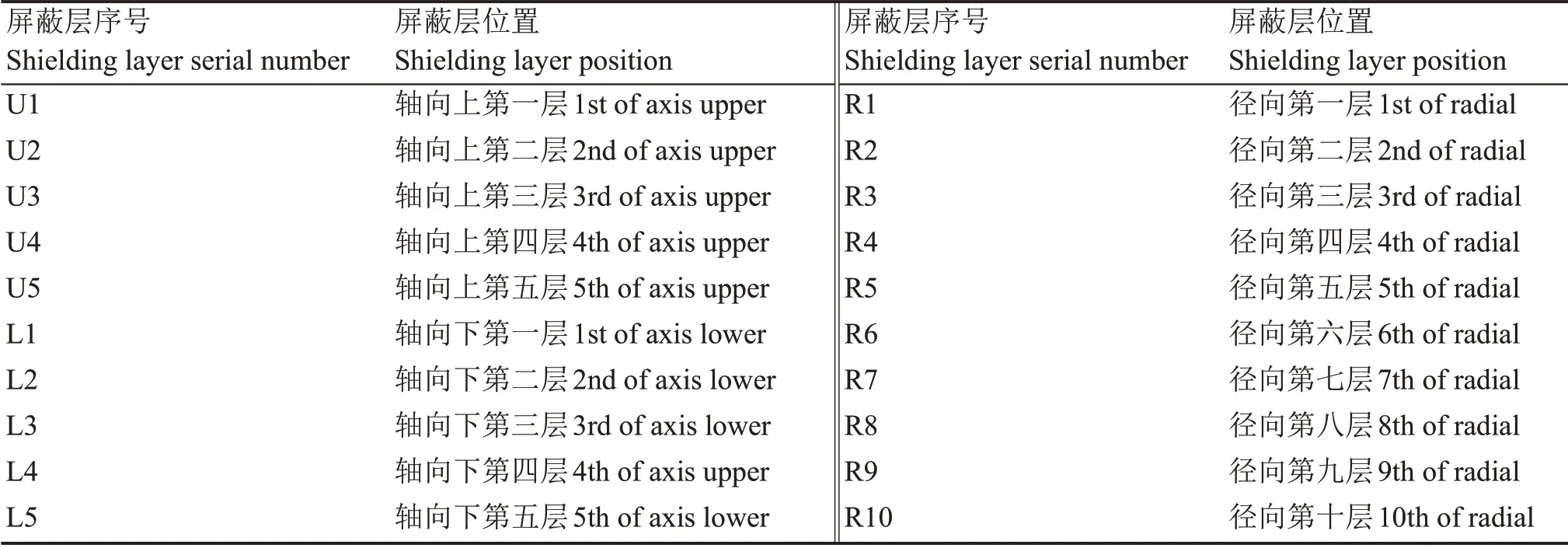
表1 屏蔽层序号与位置说明Table 1 Description of the shield number and its location

图2 核反应堆三维屏蔽结构侧视图(a)和俯视图(b)Fig.2 Side view(a)and vertical view(b)of 3D shielding structure of nuclear reactor

屏蔽方案的材料、屏蔽层厚度和屏蔽层位置等关键设计参数，以经过特定编码后生成的二进制数组表示，二进制数组与方案呈一一映射关系。以合理约束设定规避生成不具有可行性的方案，然后在各参数取值范围内随机抽样产生新方案，所有新方案的集合构成一个初始解空间。

2.2 屏蔽结构方案适应度值计算方法

屏蔽结构方案寻优过程中，方案以二进制数组形式存在，经译码（即反向编码）操作获取方案的关键设计参数，便可使用理论公式计算方案的屏蔽层重量、体积。因屏蔽性能的求解需借助屏蔽计算程序开展，且程序计算需要读取特定格式文件（屏蔽计算模型），故依照方案关键设计参数和待优化三维模型结构生成特定屏蔽计算模型，调用屏蔽计算程序完成各个区域辐射剂量率的求解。

本文基于蒙特卡罗模拟计算程序（Monte Carlo N-Particle Transport Code，MCNP）开展屏蔽计算分析，选取屏蔽层最外侧轴向上方平面、轴向下方平面和径向侧面平面三个位置开展区域辐射剂量率的求解。求解的辐射剂量率为人体（或其他生物体）单位时间所受到的辐射强度，基于粒子通量-剂量率转换因子（来自美国国家标准ANSI/ANS-6.1.1-1977）将MCNP求取到的粒子通量密度转换后获得，因MCNP的粒子输运计算是模拟单个粒子的输运过程，故求解的剂量率结果为归一化剂量率。为了提高计算效率，采用了多核并行、重要性减方差及多群输运等手段，采用相应方法后的计算资源对比如表2所示。

表2 MCNP计算资源对比Table 2 MCNP computing resource comparison

从表2可以看出，多核并行方法可显著加快运算速度，但占用了大量内存；重要性减方差方法可有效提高求解精度，但耗费了大量时间；多群输运方法同时减少了内存占用和运算时间，却牺牲了部分计算精度；综合使用这三种方法后，内存占用略微减少，运算速度和计算精度显著提高，进而有效提高了辐射屏蔽计算效率。

2.3 屏蔽结构方案性能评价方法

对不同三维屏蔽结构设计方案进行性能评价时，在单目标（如屏蔽层重量）情况下，屏蔽结构设计方案的屏蔽层重量越小，则方案性能越优。但在多目标情况下，由于每个屏蔽结构设计方案具有多维属性（如屏蔽层重量、体积、分区剂量率等），评判方案性能优劣不能简单依靠数值大小关系进行直观判断。

利用Pareto支配［11］作为屏蔽结构设计方案的性能评价方法，即当两个方案间存在Pareto支配关系时，其中处于支配地位的方案性能将优于处于被支配地位另一方案。对于方案集合中任意两个方案Xu和Xv，如果Xu和Xv满足下列条件就认为XuPareto支配Xv，简称Xu支配Xv：

当Xu和Xv之间不存在相互支配情况，且Xu和Xv也并不完全相等时，则Xu和Xv互为非支配，两方案无法直接进行性能比较。

依照各方案间的支配关系对当前方案集合进行快速非支配排序（图3）。首先对于每个方案计算两个数值：支配该方案的方案数目np，被该方案支配的方案集合Sp。当前所有支配计数np为0的所有方案，构成第一层非支配层，存入F1层。检索F1层内所有方案的支配方案集合Sp，将其内方案的支配计数np减1，当任何方案的支配计数np变为0时，将其取出存入F2层，构成第二层非支配层。如此往复，直到所有的解都被存入对应分层内。其中，方案所在的非支配层序号越靠前，代表该方案在当前方案集合中的适应度越好，越容易将遗传信息传递给下一代方案。

图3 快速非支配排序流程图Fig.3 Flow chart of fast nondominated sorting

对于解空间内的任意一个方案Xw，当且仅当解空间内不存在可支配Xw的方案，便称Xw为Pareto最优解，其特点是：无法在改进任何目标属性的同时不削弱至少一个其他目标属性。面对三维屏蔽结构高维多目标优化问题，由于各目标间存在冲突无法同时优化，故而不存在于所有目标上都能达到最优的方案，进行优化研究的目的是为了能够更快得到更贴近真实Pareto最优解集的方案集合。

2.4 屏蔽结构新方案生成方法

通过模拟生物体产生子代过程，修改用于表征方案的染色体（一组二进制数），从而实现新方案的生成，该过程主要由选择、交叉和变异操作三部分组成。

选择操作采用二元锦标赛选择策略：每次从当前方案集合中抽取两个方案，判断两方案间的支配关系，复制位于支配地位的方案加入配对库中，当两个方案互为非支配时需自定义选择规则（如为了获得更小的屏蔽层重量和体积，选择重量与体积和更小者复制加入配对库），重复操作直至交配池方案数目等于集合规模大小。交叉操作采用单点交叉策略：在配对库中任选两个方案，随机选择染色体上的位置点，交换两染色体位置点同侧部分，从而得到两个新的染色体，即两个新方案。变异操作采用位翻转突变策略：依照给定变异概率，对于符合变异触发行为的染色体，随机选取该染色体上的一个基因进行翻转。

2.5 屏蔽结构方案集合选择策略

基于精英策略，将当前方案集合Pt与产生的新方案合并为一个大集合。选择将该大集合内非支配层较低的方案进入下一代方案集合Pt+1内，直到将第Fl层的全部个体选择到Pt+1，使Pt+1规模与Pt规模相等，若将第Fl层的全部个体选择到Pt+1，下一代种群Pt+1规模大于Pt规模，则基于参考点抽样选择策略挑选第Fl层适量个体填补至Pt+1，令Pt+1规模等于Pt规模。

基于参考点抽样选择策略是解空间方案多样性的重要保障，在屏蔽结构高维多目标优化问题中还是种群收敛的有力保证。其操作流程如下：

采用预定义结构化方式生成参考点，将参考点放置于超平面内（超平面分布图如图4所示）。对可能被选择的Fl层所有方案进行自适应归一化处理，再将参考点与原点连接，并视连接线段为参考线，计算每个方案与参考线的垂直距离，与参考线垂直距离最小的方案被关联至相应的参考点（关联示意图见图5）。计算前l-1层方案关联至各参考点的数目，记变量ρj为第j个参考点关联的前l-1层方案中的方案数目。设集合Jmin={j：arg minj ρj}为拥有最小ρj的参考点集，当该集合包含多个元素时，从中随机挑选jˉ∈Jmin。

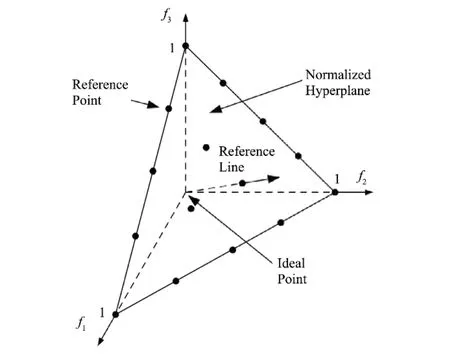
图4 三维归一化的超平面分布图Fig.4 Distribution map of 3D normalised hyperplane

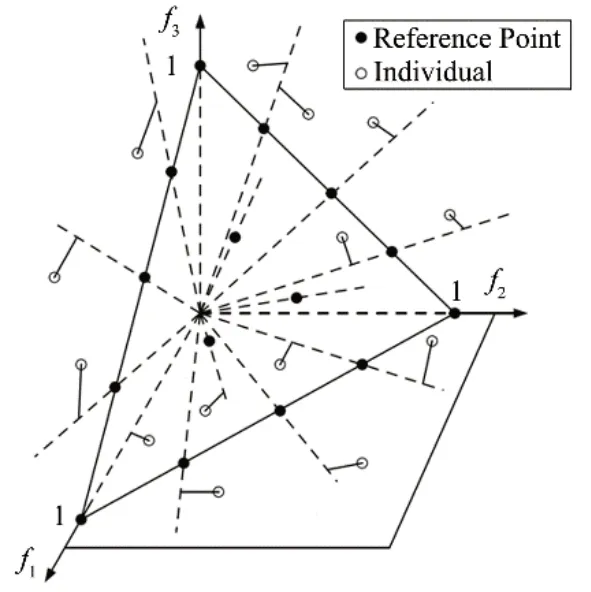
图5 三维归一化的超平面下关联操作示意图Fig.5 Schematic diagram of association operation under 3D normalised hyperplane

当ρˉJ=0时，选择Fl中与参考线垂直距离最近的方案加入Pt+1，同时参考点jˉ的ρj增加1；如果Fl无个体被关联至该参考点jˉ，则该参考点在本次选择中不予考虑。当ρˉJ＞1时，任意挑选Fl中一个方案加入Pt+1，同时相应的ρj增加1。重复该操作，直至种群集合中满足需要选择的方案数目。

3 三维屏蔽结构优化分析与数值验证

高维多目标方法与传统多目标方法的中时间复杂度皆为O（N2M），其中，N为种群大小，M为目标数，故而算法层面两方法的计算资源消耗相近。为验证本文方法可行性与有效性，构建核反应堆三维屏蔽结构模型作为优化对象（图2），并随机生成初始屏蔽方案（具体初始屏蔽方案详细参数如表3所示）。

表3 参考模型初始屏蔽设计参数Table 3 Initial shielding design parameters for the nuclear reactor

以屏蔽层总重量、屏蔽层总体积、屏蔽结构轴向最上方平面辐射剂量率、屏蔽结构轴向最下方平面辐射剂量率和屏蔽结构径向最外侧圆柱面辐射剂量率5个目标为待优化目标。将种群规模参数设置为210，最大优化代数设置为100，随机产生初始方案集合，基于该初始方案集合，由本文高维多目标优化方法（Many-objective Optimization）与传统多目标优化方法（Multi-objective Optimization）分别开展优化计算（可选屏蔽材料如表4所示），并绘制Pareto前沿均值变化趋势图（图6～8）和末代种群方案平行坐标图（图9）。

表4 优化过程可选屏蔽材料库Table 4 Optional shielding material library for the optimization processes

均值变化趋势图内以初始种群的Pareto前沿均值为单位1，对其他各代Pareto前沿均值作归一化处理。实线表示本文高维多目标方法指导寻优下Pareto前沿均值，虚线表示传统多目标方法指导下Pareto前沿均值。

从图6～8可见，在寻优结果方面，本文高维多目标方法所得最终均值皆小于传统多目标方法，特别是重量维度上本文方法的最终均值仅为传统方法的10.23%，本文方法寻优性能具有明显优势。在寻优过程方面，本文高维多目标方法在体积、重量、轴向上方剂量率和轴向下方剂量率四个维度的寻优过程中Pareto前沿均值持续低于传统方法，径向侧面剂量率维度方面前段进程次于传统方法，后段进程不相上下，故而整体来看，本文方法具有更好的全局收敛能力。

图6 目标体积(a)和重量(b)Pareto前沿均值变化趋势图Fig.6 Trend chart of frontier mean change of Pareto of objective volume(a)and weight(b)

本次模拟侧重于对屏蔽层重量与体积的优化，而重量、体积目标的优化大概率使辐射剂量率相关目标的劣化，故图中辐射剂量率相关目标均值皆呈现增长趋势，但实际工程应用中剂量率目标满足限值即可。

末代种群方案平均坐标图以随机生成的初始屏蔽方案的各目标值为基准，对末代种群方案相应目标值作归一化处理，其后投射末代种群方案的各目标值至相应的竖轴上，再以线段连接同方案的各目标值点，最终完成绘制，其中，红线粗虚线对应初始屏蔽方案，图9（a）为传统多目标优化方法下末代种群方案平均坐标图，图9（b）为本文高维多目标优化方法下末代种群平行坐标图。

从图9可见，除轴向上方剂量率维度初始屏蔽方案目标点高度相近，其他维度上本文方法的初始屏蔽方案目标点位置均高于传统方法，于重量维度上本文方法的优化比例更是达到了96.67%，远高于传统方法的56.19%。说明本文方法相较于传统方法有更大概率生成优于初始屏蔽方案的较优方案，具有更好的屏蔽方案优化能力。

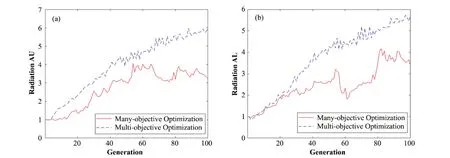
图7 目标轴向上方(a)和向下方(b)剂量率Pareto前沿均值变化趋势图Fig.7 Trend chart of frontier mean change of Pareto dose rate of objective radiation dose rate of axis upper(a)and axis lower(b)

为进一步科学评价两种方法的综合性能，选用超体积（Hypervolume，HV）指标作为衡量方案集合收敛性与分布性的性能指标，反映集合方案第一层非支配层与参考点构成目标空间中区域的体积大小，其值越大，便说明优化方法的综合性能越好。从图10可以看出，随着迭代数目增加，高维多目标优化方法指导下的方案集合HV指标整体呈现递增趋向，其收敛性、分布性表现良好，当前所得方案集合依旧能进一步被优化；而传统多目标优化方法指导下的方案集合HV指标，自29代后呈现波动变化，HV值无明显升高，说明其方案集合后续迭代陷入停滞，其分布性与收敛性再无明显提升。

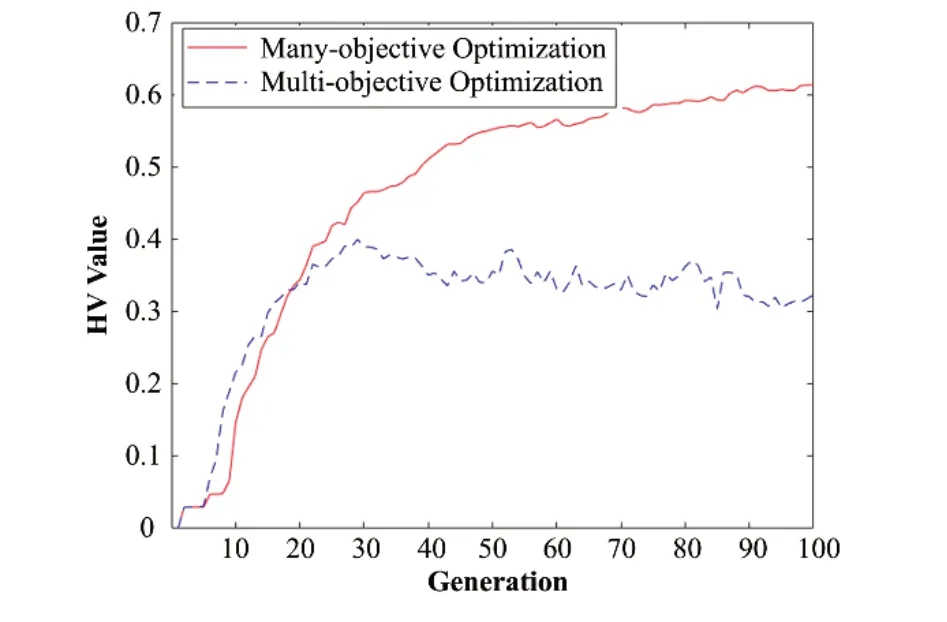
图10 HV指标对比示意图Fig.10 Schematic diagram of HV index comparison

从两优化方法寻优所得到的Pareto解集中，筛选出在体积、重量、轴向上方剂量率、轴向下方剂量率和径向侧面剂量率5个目标值上皆小于初始屏蔽结构方案的方案。传统多目标优化方法下仅得到一个更优方案，记为94号方案；高维多目标优化方法下总共可得到三个更优方案，记为97号、111号和149号方案（具体设计参数及目标值参见表5）。显然，高维多目标优化方法在三维屏蔽结构优化问题中具有更强寻优能力，可发现更多更优方案。

表5 优化方案详细设计参数及目标值Table 5 Detailed design parameters and target values for the better scheme

对比4个更优方案的优化效果（表6）：方案87对重量和径向侧面处剂量率优化程度最大，分别达75.79%与54.08%，方案111对体积优化程度最大达14.10%，方案149对轴向上下两个方向的剂量率优化程度最大，分别达到了54.54%与94.67%。在实际工程应用中，设计者可根据实际需求在以上三个方案中选择一个最佳方案。可见，本文高维多目标优化方法在三维屏蔽结构优化问题中能取得更好地优化效果。

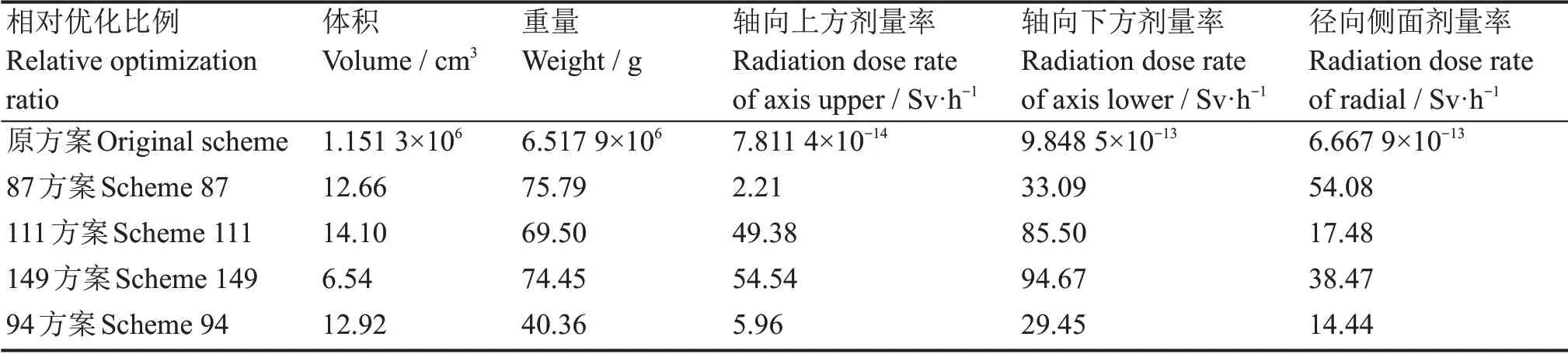
表6 初始方案目标值及各优化方案相对优化比例（%）Table 6 Initial scheme target values and relative optimization ratios for each optimized scheme(%)

4 结语

本文将高维多目标优化算法引入核反应堆辐射屏蔽优化设计领域，提出了基于NSGA-Ⅲ的三维屏蔽结构优化方法，并与传统进化多目标优化方法开展了对比分析，结论如下：

1）通过分析Pareto前沿均值变化趋势图、末代种群方案平行坐标图、HV指标和优化方案结果，验证了本文方法的有效性与实用性。相比之下，基于NSGA-Ⅲ的高维多目标优化方法在三维屏蔽结构高维多目标优化问题上具有更稳定的收敛性和更优异的全局性，可为各种新型核反应堆复杂屏蔽优化设计提供新的理论与技术支撑。

2）面向高维多目标问题中存在非支配解占比过多的现象，本文方法通过分解策略保持了高效寻优能力，但寻优完成后的Pareto最优解集（其中包含大量较优解），仍需设计者进行人工二次筛选。后续可引入设计者的偏好信息，进行Pareto最优解集的自动筛选排序，或将偏好信息作为Pareto支配关系的补充引入优化过程开展相关研究。

作者贡献声明张华健：制定论文研究工作方法、框架和思路，编制论文稿件；陈珍平：负责完善研究方案、审阅修订稿件和提供理论指导；刘程伟：负责协助开展算法对比研究与数据分析；杨超：负责对文章的屏蔽计算方法进行指导；谭波、甘斌、陈富财：负责提供模型数据、对比分析和方案研讨；于涛：负责指导完善研究思路和提供理论指导。