蒸汽发生器二次侧pH分布的模型研究

肖发亮 钟婷婷 付威伶 康晓言 邓水全

1（福州大学化学学院 福州 350108）

2（中国科学院福建物质结构研究所结构化学国家重点实验室 福州 350002）

3（福建师范大学化学与材料学院福州350007）

4（中国福建光电信息科学与技术创新实验室（闽都创新实验室）福州350108）

蒸汽发生器作为连接一、二回路的重要部件，保证其在核电站中安全经济运行非常重要［1］。蒸汽发生器作为核电站中容易损坏的设备之一，在常温下二回路水pH值小于9.6时，管道和碳钢设备易发生腐蚀［2］，此外产生的腐蚀产物会造成蒸汽发生器中污垢沉积增加，导致二次侧水流受限，降低换热效率，给核电站运行造成安全隐患。当二回路水中碱化剂浓度较高时，高pH值的二回路水会降低树脂床的使用寿命。一般情况下，在300℃时保证二回路水各处pH值稳定在6.6以上（此温度下中性水pH值为5.5）较为合适［3］。当二次侧水流经传热管与支撑板连接处、弯管和接头等区域时，其流速和温度会发生改变，因而会改变该局部区域溶液的酸碱平衡，导致其pH值发生变化，二次侧水在这些地方的pH值分布梯度较大，易发生腐蚀现象。为了减缓管道的腐蚀和污垢沉积，需要在二回路给水处加入碱化剂，调节整个蒸汽发生器二回路的pH值，保证这些区域具有合理的pH值，从而防止管道发生腐蚀［4］。因此，研究二回路水中不同位置的pH值分布是目前急需解决的现实问题。

目前，中国大部分核电站采用氨作为碱化剂来减缓蒸汽发生器中传热管的腐蚀。然而氨由于挥发性较大，容易进入汽相导致液相pH值降低，并且氨的水解平衡常数随着温度的升高而降低［5］，达到预期pH值所需要的氨量会增高。乙醇胺的水解平衡常数较大，相同摩尔浓度下其pH值大于氨，并且汽液分配系数较小。随着温度的升高，水解平衡常数的变化与氨相比不敏感。然而单独使用乙醇胺由于其价格较高会提高经济成本。因此，部分核电站开始使用氨与乙醇胺的混合液作为碱化剂来弥补单独采用氨或乙醇胺的问题［6-7］。

目前已有研究工作者通过实验的方法研究了碱化剂对管道材料的腐蚀情况［4，6-8］。蔡金平等［9］通过二回路流动加速腐蚀实验研究了乙醇胺与二回路材料的相容性，为乙醇胺作为碱化剂的应用提供了依据。然而由于二回路的实际状况非常复杂，对于在二回路中的传热管与支撑板连接处、弯管和接头处等各个局部的pH值也难于用实验进行监测，目前，有关二回路水中pH值的实验并不能准确反映真实蒸汽发生器的实际工况，使得实验结果无法准确评估二回路水中易腐蚀部位的pH值情况。因此，理论模拟成为不得不使用的研究手段。

Ferng等［10］基于多孔介质模型采用有限元方法计算了不同工况下蒸汽发生器传热管外二回路水的热工水力特性，通过研究力学因素分析了管道流致振动损伤等相关问题。孙宝芝等［11-16］通过有限元模拟研究了各种类型各种工况下蒸汽发生器传热管的热工水力特性，其计算得到的传热效率和应力等结果为解决传热管流致振动等问题提供了参考。赵永福等［3］使用美国电力研究院设计开发的程序（PCS4.0）研究了核电站二回路系统主要部位在25℃时的pH值及复合碱化剂的影响。该软件及其他类似的商业软件［17］，均依赖于未发表的经验公式，难以评估计算结果的近似程度，也难以用作预测性的工具。据我们所知，目前国内还缺乏类似的软件。

要实现核电站二回路系统中腐蚀问题的预测性研究，pH值的分布是必须解决的一个关键性问题。而目前实际采用的软件［17］，一方面在技术上完全依赖于试验数据及相应的经验公式，另一方面，知识产权也完全属于国外，是名副其实的卡脖子问题。本文首先建立了含有碱化剂的二回路水中重要离子之间温度相关的局部平衡关系，进一步通过有限元方法研究了二回路水中的温度场分布，以此为基础计算模拟了相应的pH值分布。本工作研究了任何单一或两种碱化剂的情况。在本文的研究中，作为初步的探索，我们仅研究了带有支撑板的直管二次侧水中pH值的分布。文中建立的方法不难推广用于模拟大型真实模型中的pH分布。这一研究为评估核电站二回路中pH值的分布提供了新的途径。

1 模型

蒸汽发生器由于体积大、换热管数量多、管壁薄、管间距（管圆心到相邻管圆心的距离）小，难以实现全尺寸数值模拟。考虑到蒸汽发生器真实情况的复杂性，同时由于之前没有关于蒸汽发生器中pH值整体分布的理论研究，作为实际大型模拟的初步探索，本文采用简化的直管模型，研究了直管二次侧区域水中pH值的分布情况。以管板上0～3.8 m处的直管二次侧作为研究对象，根据真实蒸汽发生器中的情况分别在管道的1 m、2 m和3 m处设置了支撑板，图1为本研究采用的直管模型。该模型由6根传热管的中心线围成的六棱柱扣除掉其中传热管及管内一次侧水和支撑板占有的区域形成。根据实际核电站蒸汽发生器传热管道尺寸，设计以下模型尺寸数据：管径为19.05 mm，管壁厚为1.09 mm，直段高度为3.80 m，管间距为30 mm。将传热管截面圆三等分，以其中一份的弦长为一个长方形的长，并在管间距的一半位置设置另一长方形的边。如图1所示，该长方形远离传热管一侧的两个直角分别用半径为1/4管径的内切圆的90°圆弧作光滑处理；六角棱柱内扣除传热管和这些光滑处理的长方形区域为支撑板（蓝色区域），其厚度为30 mm。图1中灰色区域为支撑板处二次侧水路的截面图。图1右上侧的放大区域为流水孔，根据图1中给出的几何数据可以计算出支撑板的横截面积和体积以及二次侧水体积等。管壁材料设置为Inconel690，材料属性相关参数见表1。

图1 直管模型示意图，粗实线部分所围区域为模型截面图（灰色为二次侧水，蓝色为支撑板）（彩色见网络版）Fig.1 Diagram of straight pipe model,the area enclosed by the thick solid line is the cross section of the model(the grey part denotes the water in the secondary circuit,the blue part denotes the tube support plate)(color online)

表1 传热管、支撑板材料物理属性Table 1 Physical parameters of relevant materials

2 计算方法

2.1 含碱化剂水中的酸碱平衡

核电站二回路水系统中通过添加碱化剂来防止回路设备发生腐蚀，进而提高设备的使用寿命。早期核电站使用单一的碱化剂来调节二回路系统的pH值分布。采用单一碱化剂时二回路水中的解离平衡关系如下：

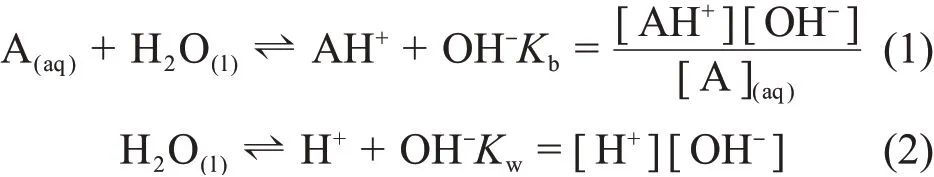
式中：A为某种碱化剂，比如氨；Kb为碱化剂的水解平衡常数；Kw为水的解离平衡常数。根据溶液中阴阳离子浓度电荷守恒可得如下关系：

令cl=[AH+]+[A](aq)，将其代入式（3）可得[OH-]的计算方程：

式（4）为水溶液当中含单一碱化剂时氢氧根浓度所需要满足的方程。当加入的碱化剂为氨时，将氨在二回路水中的浓度c1、Kb和Kw代入到式（4）中可计算得到此时的氢氧根浓度，其中Kb、Kw为温度的函数。

当溶液中存在两种碱化剂时，应满足以下两种碱化剂在二回路水中的解离平衡关系：

根据溶液中电荷守恒关系可知，

其中：式（5）、（6）中A和B为两种不同的碱化剂，令c1l=[AH+]+[A](aq)，c2l=[BH+]+[B](aq)，由 此 可推出式（9）：

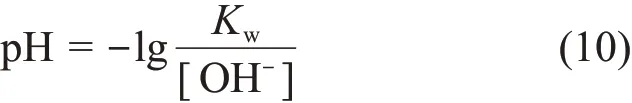
式（9）为水溶液当中含两种碱化剂时氢氧根浓度所需要满足的方程。由于二回路水中的pH值主要由式（5）～（7）中的三个平衡决定，其他杂质离子对酸碱平衡的影响可以忽略不计，因此式（9）略去了其他阴阳离子对pH值的影响。式（9）可以应用于二回路中任何区域的局部平衡，对于任何两种碱化剂都适用。本文试用的两种碱化剂A为NH3，B为HOCH2CH2NH2。

除了上述平衡外，在实际使用中碱化剂本身还存在汽液两相的平衡问题。对于氨与乙醇胺，该平衡可以用如下定义的相对挥发度RV来描述，氨与乙醇胺的相对挥发度RV定义如下：

由上述定义可得液相中碱化剂的浓度计算公式为：

式中：c为二回路水中碱化剂（氨或乙醇胺）的浓度；c1为液相中碱化剂（氨或乙醇胺）的实际浓度。

根据文献［5，18-20］，本文所用氨与乙醇胺在水中的解离常数和相对挥发度随温度变化的值见表2，其中温度在～573 K附近的值对应于核电站的压强条件，即～6.8 MPa。

根据表2中的数据，氨与乙醇胺在表中温度范围内的解离常数和相对挥发度可以通过分段立方厄密多项式［21］内插得到。水的解离常数由式（14）［22］计算得到：

表2 氨与乙醇胺在不同温度下的解离常数和相对挥发度Table 2 The dissociation constant and relative volatility of NH3 and ETA at different temperatures

由于Kb1、Kb2、Kw是温度的函数，假设氨和乙醇胺在水中的浓度为已知参数时，氢氧根离子浓度就是一个关于温度的函数，根据这一函数关系，由于温度场依赖于二回路水的位置，所以，氢氧根离子的浓度场决定于二回路水的温度场。本文首先计算二回路水中温度场的分布情况，然后采用上述关系计算得到二回路水中氢氧根的浓度场分布，进而得到二回路水pH值的分布情况。

2.2 不同碱化剂总浓度下限的估计及相应各组分浓度的计算

核电站运行期间要求在一定的工作温度范围内，在557～578 K之间［23］，二回路水各处的pH值能稳定在6.6以上［24-26］。由于pH值随温度的增加而降低，因此，二回路中pH值的下限一般出现在二回路温度最高处。在本工作中，我们选定～573.15 K为温度的上限，以此来估计二回路中碱化剂总浓度的下限。本工作分别考虑了三种不同情况下的总浓度：1）单一氨水；2）以摩尔浓度比NH3∶ETA=8∶1估计的总浓度；3）NH3∶ETA=1∶1时的总浓度。对情况1），根据式（4）计算出573.15 K时，c1=2.038 mol·m-3；再根据式（13）和表2可计算出c=8.784 mol·m-3。对情况2），设氨为组分1，ETA为组分2，设定它们的摩尔浓度比为8∶1，根据式（13）和表2可以计算出573.15 K时，c1l∶c2l=2.47∶1；再利用式（9）、（10）和pH=6.6，可分别求出c1l和c2l；在此基础上，用式（13）可计算出c1=4.040 mol·m-3，c2=0.505 mol·m-3。为考察氨与乙醇胺不同比例的影响，锁定它们的浓度之和c1+c2为定值，即：4.56 mol·m-3。在该条件下，可设定不同的摩尔浓度比值：1∶0、8∶1、4∶1、2∶1、1∶1、1∶2、1∶4、1∶8，分别算出各组分相应的浓度，其中1∶0对应于c=4.56 mol·m-3时，单一氨的情况。情况2）的计算结果列于表3中。采用类似的方法，可以计算情形3）各组分的浓度，计算结果列于表4中。

表3 总浓度为4.56 mol·m-3时不同预设配比下氨与乙醇胺在二回路模型中的浓度①Table 3 The calculated concentrations of NH3 and ETA in the secondary circuit model with c1+c2=4.56 mol·m-3①

表4 总浓度为1.8 mol·m-3时氨与乙醇胺不同预设配比下在二回路模型中的浓度Table 4 The calculated concentrations of NH3 and ETA in the secondary circuit model with c1+c2=1.8 mol·m-3

2.3 传热方程

本文利用COMSOL Multiphysics中的气泡流和流体传热物理场进行耦合计算。气泡流物理场是一种简化的双流体模型，在计算时做出以下假设：气体密度与液体密度相比可以忽略不计；气体相对于液体的运动是由黏性阻力和压力之间的平衡决定的；两相具有相同的压力场。基于以上假设，采用以下守恒方程进行计算。

蒸汽发生器传热管外二次侧水的传质过程用质量守恒方程来描述：

动量过程由动量守恒方程描述：

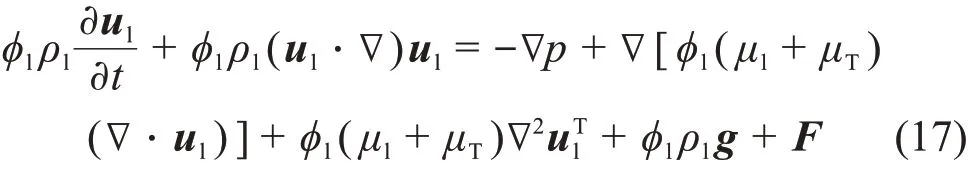
热传导过程用能量守恒方程来描述：

其中：

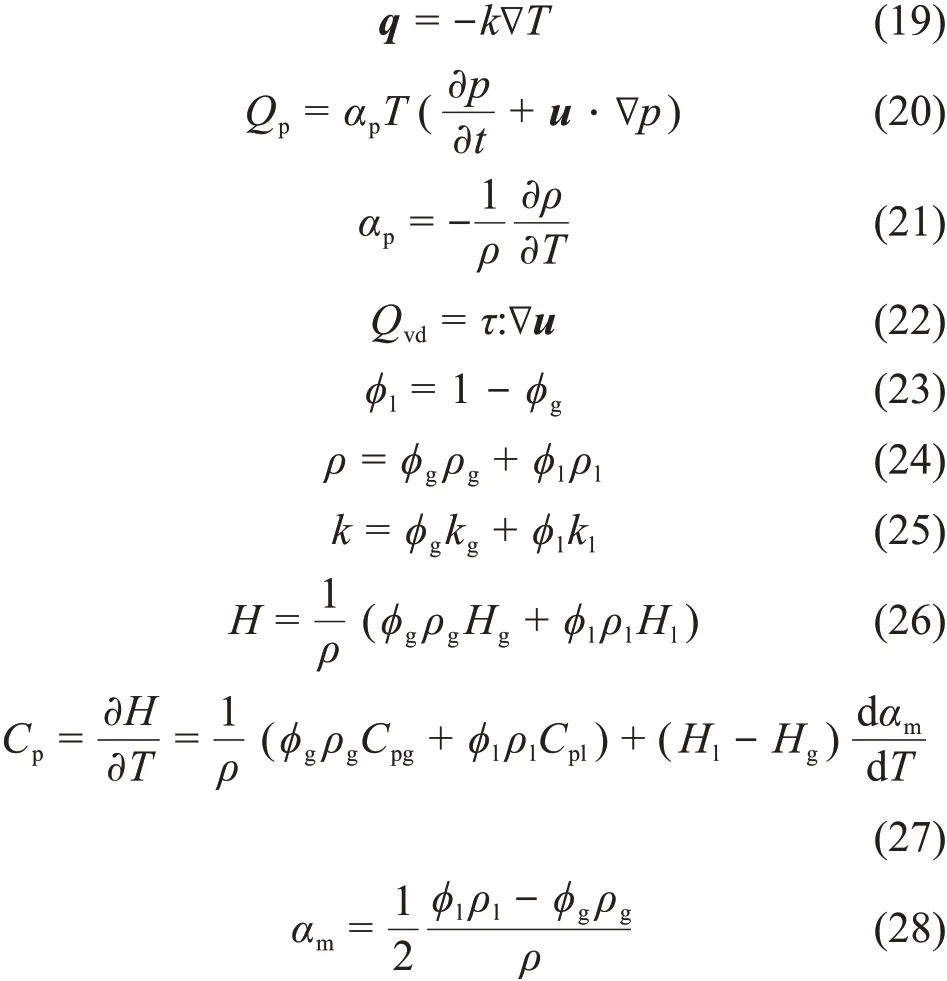
式中：ρ、Cp、k、ϕ、u、p、μl和μT分别表示二次侧流体的密度、比热容、导热系数、相体积分数、速度矢量、压强、液相动力黏度和湍流黏度，下标l和g分别表示液相和汽相。mgl为汽相向液相的传质速率；F和g分别是其他额外的体积力和重力矢量；q和qr为传导热流和辐射热流；Qp为单位时间单位体积压力所做的功；αp为热膨胀系数；Qvd为流体中的黏性耗散；τ为黏性应力张量；Q为黏性耗散以外的热源；H为焓；αm为质量分数。

在本研究中，假定传热管壁与二次侧流体之间无滑移，即无额外体积力作用，即F=0。在研究中不考虑辐射对传热的影响，即qr=0。当温度约为558.5 K（压强为6.8 MPa）时，二次侧液相水与汽相水的生成焓差值为Hl-Hg=1 508.8 kJ·kg-1［27-29］。

基于气泡流物理场的假设，对上述公式中的部分物理量进行以下处理。

汽相的密度采用理想状态气体方程计算：

其中：水蒸气的摩尔质量M为18 g·mol-1；理想气体常 数R为8.314 J·(mol·K)-1；参 考 压 强pref为101 325 Pa。压强p和温度T作为位置的函数，随流体位置的不同而变化。

式中：uslip为两相之间的相对速度，这里采用均相流，汽相与液相之间无滑移，即uslip=0；udrift为汽相的漂移速度；μT为引起漂流的有效黏度，即该模型中的湍流黏度，可根据气泡流物理场中的湍流动能、液相动力黏度计算［30-32］。

汽相与液相的压强相等，即pg=pl。

相关数据采用IAPWS数据库中汽液两相时水的相关热力学属性参数［27-29］，具体见表5所示。

表5 汽态及液态水的相关热力学参数Table 5 Thermodynamic parameters of water in its gas and liquid states

3 初始条件和边界条件

根据核电站蒸汽发生器的实际运行参数，针对图1所示模型，设置如下边界条件：在二次侧水入口处设定水流速度和温度，出口处设定压强，同时考虑轴向高度方向上重力的影响。由于本研究主要针对传热管二次侧水，因此将一次侧的作用简化为向二次侧加热的热源，即在传热管壁处对二次侧水设定一个热通量，参考文献中的热通量表达式［14］，设定其算式如表6所示；很明显，图1中所取的模型具有3次对称轴，并且在六角模型的边界上每个实线部分都代表一个对称面。模拟中，汽相密度与汽相体积分数的初始值设为0。蒸汽发生器传热管二次侧的边界条件设定如表6所示。

表6 主要边界条件参数Table 6 The boundary values of main parameters

4 结果与讨论

在核电站蒸汽发生器中，三叶梅花支撑板主要对传热管起固定作用，限制传热管横向位移，但是，它也影响了二次侧水的流动状态。图2为根据研究模型所计算的二次侧水流速度分布状况。

图2 研究模型中二次侧水流速度分布状况(a)不同高度横截面上的平均流速，(b)z=1.5 m,2.0 m,2.5 m处横截面上的流速分布，(c)z=2.0 m附近的纵向剖面上的流速分布，剖面的位置见(b)中的虚线Fig.2 Calculated distribution of the fluid velocities in the secondary circuit model(a)Average velocity over cross sections at various heights,(b)Velocity distributions on three selected cross sections at z=1.5 m,2.0 m,2.5 m,respectively,(c)Velocity distribution on the longitudinal section nearby a support plate at z=2.0 m,see the dashed line of(b)for the location of the section

从图2（a）可见，二次侧不同高度截面上的平均水流速度保持在1 m·s-1左右，仅在支撑板附近明显增加。二次侧水流量恒定，支撑板处的水流横截面积比无支撑板处小得多，根据伯努利定律（流体机械能守恒），横截面积越小流速越快，因此支撑板处平均水流速度会高于两侧。

图2（b）是二次侧在1.5 m、2.0 m、2.5 m截面上的流速分布图，图2（b）中，z=2.0 m的截面图中空白部分为支撑板。由图2（b），靠近传热管壁和支撑板边缘的水流速度要低于同一高度其他部位的水流速度，有支撑板处的水流速度最小值（1.4 m·s-1左右）比无支撑板处流速最大值（1.1 m·s-1左右）还要大。二次侧水与传热管壁和支撑板边缘相互接触的部分流速较慢，主要是受到摩擦阻力的影响。

由图2（c）可知，沿二次侧水流方向，二次侧水进入支撑板流水孔后流速明显增大；流出流水孔后，水流明显出现分层现象，如图2（c）所示，流水孔出口处截面图的一边水流速度较快，另一边较慢。结合图2（b）、2（c）可以看出，二次侧水刚流出支撑板流水孔时的流速差距最大，水流出现复杂的分层现象，易于产生湍流；随着二次侧水继续流动，流速差距逐渐减小，分层现象逐渐减弱。该现象与文献［11］中发现的情况类似。流体中局部范围内流速相差过大时容易产生湍流（如图2（c）画圈位置）。支撑板处流速过低的区域腐蚀性溶质或杂质聚集的可能性极高，这将导致沉淀的出现，促使水流状态进一步复杂化。沉淀堆积过多会挤压传热管壁造成管径减小、产生凹痕，最后由于应力作用导致管道破裂，严重影响核电站运行安全；沉淀堆积还会使传热管与支撑板间形成堵塞区域诱发缝隙腐蚀，这也是核电站备受关注的问题之一。

图3显示了二次侧水在流动方向上的温度变化以及支撑板对它的影响。随着二次侧水沿轴向流动，二次侧截面上的平均水流温度逐渐上升，在模型的z=3 m处一次侧向二次侧的传热趋于稳定，随后二次侧水流温度慢慢趋于恒定，维持在558.5 K。图3所示的结果与之前有关立式自然循环蒸汽发生器热工水力特性的实验研究中发现的温度分布类似［33］。

图4为蒸汽发生器二次侧水在不同截面上的平均体积含汽率沿水流方向的变化。由图4可知，二次侧水平均体积含汽率在z≤1 m的区间内维持在初始水平，在本模拟及其他类似的模拟［1，11，34］中一般设定为0，此阶段二次侧水处于单相区，称为预热段。从z=1 m起二次侧水中的蒸汽开始显著增加，因此，该点又被称为沸腾起始点。随着二次侧水沿轴向流动，传热管壁的汽化核心（能够贮存汽体的孔穴［35］）开始增大变成汽泡，汽泡变大后脱离壁面并向流道中心运动。二次侧水在z=2 m，3 m处遇到支撑板，它们阻碍了汽泡的运动，延长了汽泡脱离传热管壁面的时间；另一方面，水流在流过支撑板后，由于湍流的影响，会使得部分汽泡滞留在支撑板的板面［12］，这两个因素都会导致流体中含汽率的增长速率在支撑板出口侧附近有所降低，导致含汽率在支撑板处出现一个拐点。二次侧水到达z=3.5 m处时，一次侧向二次侧的传热趋于稳定，气液两相达到热平衡，汽液温度维持在约558.5 K（图3），液态水通过水的蒸发维持其相对稳定的温度，从而使得流体中的含汽率继续增长。二次侧水在模型的出口处（z=3.8 m）的平均体积含汽率为0.107，这与其他模拟中得到的值一致［1，33］。

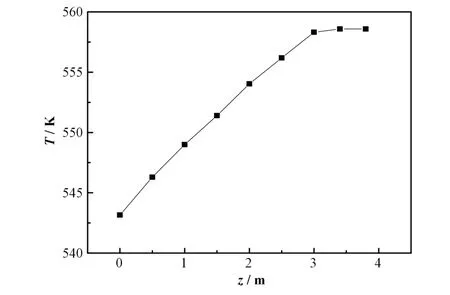
图3 二次侧模型中不同截面上水的平均温度沿水流方向的变化曲线Fig.3 Variation curve of average temperatures of water on different sections along the flow direction in the secondary side model

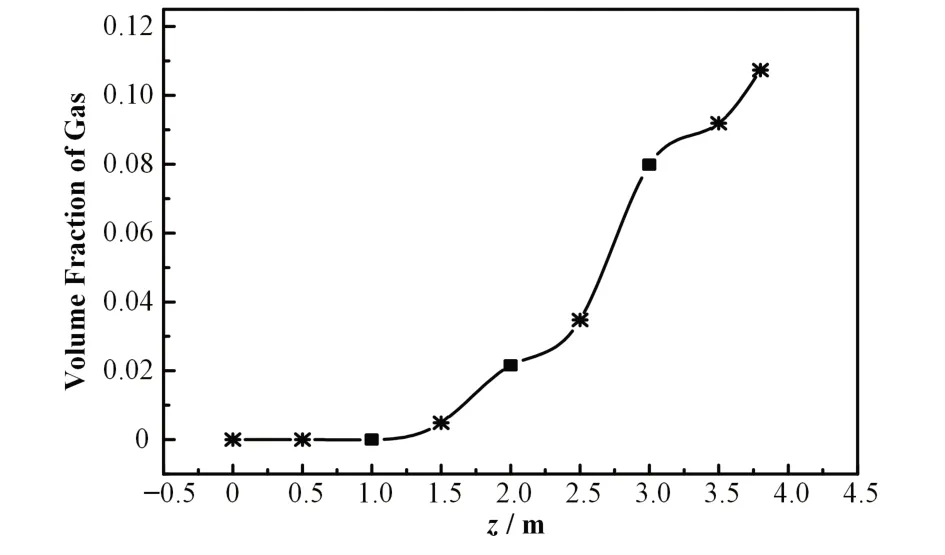
图4 二次侧模型不同高度截面上的平均体积含汽率沿水流方向的变化曲线，其中，黑色方块代表支撑板位置Fig.4 Variation curve of the average volume fraction of gas along the flow direction on cross sections at different heights of the secondary circuit model,where the black squares indicate the locations of tube support plates

图5给出了二次侧水在工作温度条件下（图3）沿流动方向在直线（12.525，0，z）上的pH值变化情况。由图5（a）可知，若使用单一氨作为碱化剂，则cNH3=8.784 mol·m-3时，在 模 拟 的 范 围 内（0＜z＜3.8 m），pH（z）＞6.65。

从图5（b）可以看出，根据核电站正常运行的要求，按NH3∶ETA=8∶1估计的总浓度为4.56 mol·m-3。如果假定总浓度不变，使用单一氨作为碱化剂（NH3∶ETA=1∶0），pH（z）＜6.6明显不合要求；而即使加入少量的ETA，如：NH3∶ETA=8∶1，二次侧水的pH值也能得到明显提升，pH（z）＞6.65，相对于此时单一氨碱化剂的情况，二者pH平均值的差异为从图5（b）可见，随着乙醇胺占比的增大，pH值的上升幅度逐渐降低，在NH3∶ETA≤1∶4以后，pH值的提升接近饱和（饱和效应，图6）。从表2可知，相同温度下乙醇胺的相对挥发度远低于氨，因此，乙醇胺的存在，提高了碱化剂在液相中的分配比例，相对于纯氨而言，能更有效地提升二次侧水的pH值，赵永福等［3］的实验也证明了这一点。图5（a）、（b）的结果表明，无论以摩尔浓度或者质量浓度为标准，适量ETA的加入都能有效降低碱化剂的使用量。

如图5（c）所示，如果进一步提高ETA的相对量至NH3∶ETA=1∶1时，二元碱化剂的总浓度为1.8 mol·m-3时即可满足二回路pH值的要求。毫无疑问，此情形下碱化剂的总用量更少！相对于图5（b）的情况而言，对于同样的碱化剂组分比，pH（z）均有所降低，这导致NH3∶ETA＜1∶1时，pH（z）＜6.55，均低于核电站运行的要求。上述模拟结果表明，根据电站的实际运行要求，和其他考量，比如：安全、经济（乙醇胺为10.35元·kg-1，浓氨水约为1.38元·kg-1）等因素，我们都可以模拟单一或二元碱化剂的用量。

如图5所示，沿二次侧水的流动方向，pH值逐渐下降，而在支撑板处略有升高。pH值是影响传热管与支撑板间缝隙腐蚀的重要因素，但是，由于二回路高温、高压、封闭的水化学环境、缝隙位置及几何尺寸的特殊性，原位测量缝隙内水化学参数非常困难，目前主要通过实验模拟缝隙内溶液水化学或用理论方法模拟局部，如：缝隙腐蚀的情况［23，36-38］。但是，这些模拟需要假定二次侧水临近缝隙处的pH值。本工作为模拟蒸汽发生器中二次侧水本体中各处的pH值提供了新的解决方案，可以为研究各种复杂局部与pH值相关的问题提供合理的边界条件。

为探究碱化剂总浓度一定的情况下，二次侧水pH值对乙醇胺浓度改变的响应特征，我们根据图5（b）、（c）的计算数据，选取1.5 m（直管处）和2.0 m（有支撑板处）的pH值分别作pH-cETA曲线，取其导数，最终得到图6的曲线（dpH/dcETA-cETA）。

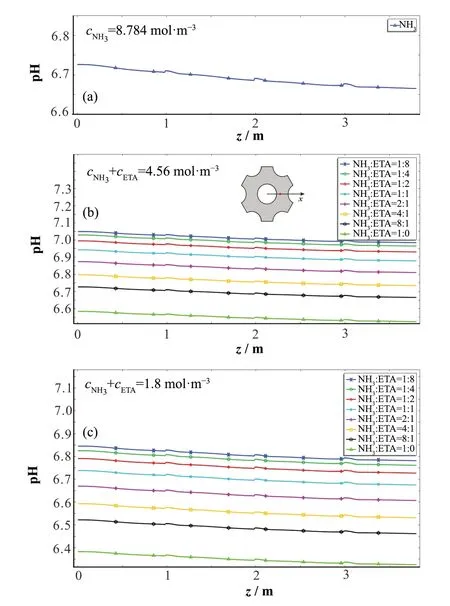
图5 二次侧水在靠近传热管壁处pH值沿轴向的变化曲线，其中样本点坐标为(12.525 mm,0,z)，0≤z≤3.8 m（见(b)中截面图）（彩色见网络版）(a)cNH3=8.784 mol·m-3，(b)cNH3+cETA=4.56 mol·m-3，(c)cNH3+cETA=1.8 mol·m-3Fig.5 Variation curve of the pH values of the water near the heat transfer tube wall along the axis of the secondary circuit model,where the sampling point coordinates are(12.525 mm,0,z),0≤z≤3.8 m(see the cross section of(b)).The various molar ratios of the binary alkalizers are also shown in the inset of the figure.(color online)(a)cNH3=8.784 mol·m-3,(b)cNH3+cETA=4.56 mol·m-3,(c)cNH3+cETA=1.8 mol·m-3

图6给出了支撑板处，z=1.5 m，及直管处，z=2.0 m，pH值在二元碱化剂的总浓度分别为1.8 mol·m-3和4.56 mol·m-3时 随ETA浓 度 的 改 变。为了探究这种改变的相对大小，我们进一步计算了每种情况下pH值导数dpH/dcETA与ETA浓度和cETA的关系。如图6中pH-cETA曲线所示，在每种情况下，ETA浓度的增加都会导致pH值的增加。但是，在碱化剂总浓度较低时，pH值的增加更快，图6中的导函数曲线，dpH/dcETA-cETA也清楚地表明了这一点。从导函数曲线也可以清楚地看到，在ETA浓度达到一定程度后，pH值的增加变缓，这一点在碱化剂浓度较大时，如图6中的4.56 mol·m-3，尤为显著，我们称之为饱和效应。图6中的4条dpH/dcETA-cETA曲线两两重合的事实表明，支撑板的存在几乎不影响乙醇胺对二次侧水pH值的提升效果。我们的模拟表明，在满足核电站安全需求的条件下，适当降低碱化剂总浓度是可行的，ETA饱和效应的存在表明盲目增加ETA的浓度并无实际意义。毫无疑问，在确保安全的前提下，这些参数可以根据实际条件、经济考量等进行优化，从而实现核电站安全、经济地运行。

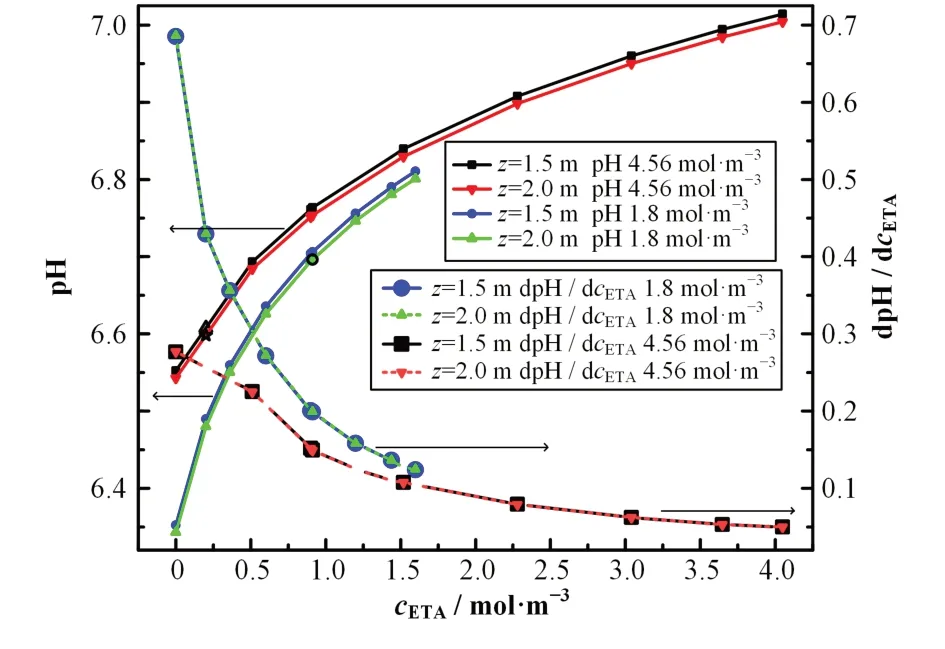
图6 (12.525 mm,0,z)线上，z=1.5 m,2.0 m处（参见图5），碱化剂总浓度分别为1.8 mol·m-3和4.56 mol·m-3时，pH值随ETA浓度变化及变化率的关系曲线Fig.6 Relation curves of pH value with ETA concentration(cETA)change and change rate corresponding to two different alkalizer concentrations(1.8 mol·m-3,4.56 mol·m-3)at z=1.5 m,2.0 m two points respectively(shown in Fig.5)

5 结语

本文首先建立了含有碱化剂的二回路水中重要离子之间温度相关的局部平衡关系，并进一步通过有限元方法研究了二回路模型系统中水的温度场分布，以此为基础计算模拟了相应的pH值分布。通过研究二回路模拟系统中不同总浓度条件下，氨与乙醇胺摩尔浓度比与二回路水中pH值分布的关系，我们发现，相对于纯氨而言，乙醇胺的存在能更有效地提升二次侧水的pH值，但是，乙醇胺对于pH值的提升也存在着饱和效应。该效应的存在以及二回路系统水的pH值分布与碱化剂总量的依赖关系为核电站安全、经济运行提供了重要的参考因素。本文建立的模拟方法，仅依赖于一些基本的物化参数，容易推广到解决实际二回路系统中水的pH的分布问题，为进一步研究二回路内部一些关键部位的腐蚀问题提供了可靠的边界条件。有关的计算公式及所用的近似易于检验和标准化，从而为发展我国在相关领域的模拟软件，奠定了初步的基础。

作者贡献声明肖发亮：负责模拟计算，数据分析，文章撰写；钟婷婷：负责数据处理及部分计算；付威伶：负责数据采集；康晓言：负责前期部分计算；邓水全：项目负责人，研究方案的构思和制订者，文章的修改和指导。