基于GPR数值模拟正演的地下介质分析方法
2022-11-18宋正淳邱哲理张雪冰覃育祥
宋正淳,邱哲理,张雪冰,孙 超,胡 昕,覃育祥
吉林建筑大学 测绘与勘查工程学院,长春 130118
0 引言
探地雷达[1]探测地下介质多为0.5 m~5 m区间内,具有无损探测、探测速度快且探测过程连续、分辨率高、操作方便灵活、探测费用低等优点.因其优点故目前广泛用于考古、矿产勘查、岩土工程勘探、工程质检、建筑结构检测以及军事勘查等众多领域中.探地雷达其工作原理是利用天线激发高频脉冲电磁波传至地下有耗介质中,地下各层有耗介质各不相同且介质具有不均匀性、各向异性、强衰减性,故接收的电磁波信号波动也不同.利用其电磁信号的差异性,可将一道道回波信号接收的振幅与时间、频率等参数来分析和推断被探测土体的地下构造并数据处理绘制成图像.而本文研究的gprMax[2]软件则是将电磁波信号模拟仿真,仿真信号波动数据处理组成B-scan图[3],届时可通过图形研究地下不同介质的位置及形态.其方法是基于时域有限差分(Finite difference time domain,缩写为FDTD)[4]的麦克斯韦[5]方程求解电磁信号强度.FDTD方法是将仿真区域拆分成一个个空间网格,用数值有限差分方法逼近麦克斯韦方程,并将时间离散化,再根据已知的初始边界条件和介质,通过数据计算处理,将一段时间内的反射信号数据进行整合,即可将仿真模型的二维或三维的数据可视化.介电常数存在差异的两个界面会反射电磁波,观察生成的B-scan图的电磁波现象,通过两组实验对比观察其极化[6]方向和相位[7]变化的规律.
1 探地雷达数据模拟
1.1 探地雷达数据模拟基本原理
从宏观上来说,所有的电磁现象均可由麦克斯韦方程解释.以下均是一阶偏微分方程,用来表示基本电磁场量与其源的关系:
×E=-∂B∂t
(1)
(2)
(3)
(4)
式中,E是电场强度,V/m;H是磁场强度,V/m;B是磁通密度,Wb/m2;D是电位移,C/m;J是电流密度,A/m2;q是电荷密度,C/m3;t是时间,s.除上述式子外,其媒质本构关系式是:
D=εE,B=μH,J=σE
(5)
式中,ε是相对介电常数;μ是磁导率,H/m;σ是电导率,S/m.基于麦克斯韦方程组下,根据模型的位置及时间的条件下求解上述方程式,得到探地雷达模拟数据.将模拟的电磁信号数据分析处理即可得到A-scan,B-scan,C-scan图像,B-scan图像即是本文主要分析研究的重点,B-scan图像可将模拟地质的地下模型剖切面用二维表示出来.
1.2 电磁波在界面的反射系数与相位变化
电磁波被探地雷达的天线激发信号射入介质界面上会发生反射和透射现象,其原理类似于光入射到水面和玻璃面.在GPR中利用反射器的传统技术可以将速度走时分析与CMP数据采集方法相结合,但确定雷达波的速度则需用反射波的传播时间来确定.其方法存在缺陷,电磁波进入介面后的回波信号深度有局限性,不能确定最低反射面以下介质的速度.电磁波从天线中释放出其电磁信号可能会产生极化,极化类型由天线的设计确定.天线的设计可以是线性的,圆形的或椭圆形的.绝大多数的探地雷达发出的波是线性的极化,线性的极化又可分为垂直极化和平行极化.极化类型决定电磁波如何反射,电磁波在界面的反射系数可定义为反射波的振幅(或能量)Er与入射波的振幅Ei之比.需要注意的是,垂直极化和平行极化的反射系数有所不同,实际探地雷达数据采集多以垂直极化为主,垂直极化的反射系数可表示为R⊥[8]:
R⊥=ErEi=ε1cosθ1-ε2-ε1sin2θ1ε1cosθ1+ε2-ε1sin2θ1
(6)
式中,ε1,ε2分别对应第一和第二层介质的相对介电常数;θ1是入射角度.
电磁波入射到不同介质时,一部分会发生反射现象,另一部分电磁波则会发生透射现象透过分界面.电磁波在界面的透射系数可定义为Et是透射波的振幅(或能量)与Ei是入射波的振幅之比.
T⊥=EtEi=2ε1cosθ1ε1cosθ1+ε2-ε1sin2θ1
(7)
式中,T⊥是垂直极化的透射系数.
理想完美电导体(Perfect Electric Conductor,PEC)不发生透射现象,是因为PEC导体的相对介电常数无穷大,当第二层介质为PEC时,上式中分母无穷大,分子是除PEC材料以外的其他非导体任意材料,透射系数T⊥趋近于零.
反射系数和透射系数之间满足公式:
1+R⊥=T⊥
(8)
电磁波的频率由发射的波源决定,探地雷达中多选择Richer型波源,频率不变.电磁波从天线释放出信号波,信号波在同种介质中传播波长不发生变化.当电磁波从介质进入其他介质中时波长会减小,振幅也会因阻尼效应减小;当电磁波靠近PEC时,电磁波不会进入PEC中而是会将电磁波反射.共享相同频率的多个采样道电磁波相互作用产生相位变化,相位变化是由两个或多个采样道电磁波波形的振幅波峰和波谷位置关系确定,通过距离、时间、度数测量相位.介面中某一点的波阻抗公式为:
η=EH=(με)0.5
(9)
式中,η是电场与磁场的复振幅之比定义为波阻抗,Ω.
2 模型建模与结果分析
因本文主要讨论的是探地雷达的高频脉冲电磁波入射到地下的电磁波相位及极化方向,而设置两层介质界面后第二层界面的入射波是来自于第一层界面的透射波,其信号波动不太明显,故拟构建两组湿沙土样为背景介质的模型(如图1,图2所示),并分别设置2组不同尺度、位置和深度的金属和空洞异常体.

图1 小尺度圆柱异常体正演模型,圆柱直径均为75 mmFig.1 The forward model of small-scale cylindrical anomalies at the cylinder diameter of 75 mm

图2 大尺度圆柱异常体正演模型,圆柱直径均为300 mmFig.2 The forward model of large-scale cylindrical anomalies at the cylinder diameter of 300 mm
2组模型均由表层0.03 m的空气和0.6 m深的湿沙构成;异常体均为圆柱形异常体,左侧2个异常体采用PEC金属电导体,右侧2个异常体均为空洞.模型一中异常体直径均为75 mm,深度依次为400 mm,350 mm,400 mm,350 mm;模型二中异常体直径均为300 mm,深度依次为350 mm,250 mm,350 mm,250 mm.在gprMax正演模拟中,选择激发源均为主频为900 MHz的Ricker子波,激发源与接受源间距均为50 mm.
不同深度与直径的两组管线模型的gprMax正演结果如图3,图4所示.

图3 小尺度圆柱异常体正演剖面,圆柱直径均为75 mmFig.3 The forward section of small-scale cylindrical anomaly at the diameter of 75 mm
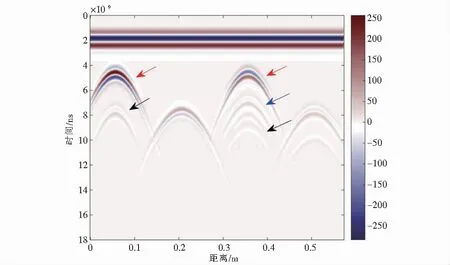
图4 大尺寸圆柱异常体正演剖面,圆柱直径均为300 mmFig.4 The forward section of large-scale cylindrical anomaly at the diameter of 300 mm
电磁波传播到存在介电常数差异的界面时会在相应位置会呈现波形,红色与蓝色分别代表正向和负向振幅,图中颜色越深代表其电场强度越强.正演模型的关键过程如下(由于两组原理类似故仅对图4过程进行描述),其中左侧PEC异常体上方的电磁波传播大致可描述为2个过程.
过程1 以图4为例.探地雷达从天线发射的高频电磁脉冲(波形约可用Ricker子波表示),其波形为一组由正向-负向-正向-负向振幅组成的子波(图中由红-深蓝-深红-浅蓝表示,见2 ns处直达波),通过较薄的空气层传入湿沙介质中.电磁波在湿沙介质中传播至PEC金属异常体表面,在剖面约时间深度6 ns处可见明显的双曲线(参见红色箭头),其颜色依次是浅蓝-深红-深蓝-浅红表示.通过对比直达波可知极性发生了反转.
过程2 电磁波经PEC异常体时反射到湿沙界面和空气界面之间,一部分电磁波透射到空气介层,另一部分又反射到PEC异常体表面处(多次波).因为一部分电磁波透射到了空气介质中,图4中黑色箭头处电磁波产生衰减,但其振幅依次为微红-浅蓝-浅红-微蓝,随后再次传播的多次波因振幅衰减在图中已无法识别.图2中左二的蓝色圆柱完美电导体由于位置距离空气界面层较远,所以图中可识别的电磁波只有一次.上述两过程中的反射系数R⊥,透射系数T⊥以及反射与透射电场强度之比Er∶Et参见表1.
对于右侧空洞异常体,电磁波传播可大致描述为3个过程:
过程1 电磁波由空气界面透过到湿沙介面之后运动到左测空心圆柱异常体顶部,有一部分透射到了空洞空气介质管内,另一部分则反射到了湿沙层顶部,回波被接收天线接收,见红色箭头处双曲线同相轴,按接收时间顺序其电场强度由浅红-蓝-红-浅蓝表示.
过程2 之前一部分电磁波透射到空洞内部后,电磁波运动到空洞底部后一部分电磁波经反射,回波被接收天线接收,见蓝色箭头位置,其颜色变化依次是微红-浅蓝-浅红-微蓝.
过程3 当电磁波传播到湿沙与表层空气界面时,一部分经反射又传播到空洞顶部,部分电磁波经反射后又回到地表被接收天线接收,在图4黑色箭头处产生电磁波,电场强度颜色变化依次是微红-微蓝-微红-微蓝.左二与左四情况相同均因埋深较深且没有进行衰减补偿处理,所以后续多次波不明显.
通过图片对比发现电磁波在湿沙界与PEC界面颜色不发生改变,正负极振幅不发生改变.电磁波由湿沙界面到圆柱空心管或由空心管到湿沙界面时,颜色发生改变,正负极振幅发生相位变化.其原因是完美电导体没有介电常数,不发生透射,只有反射,极化方向不发生改变.空心管则是由高介电常数向低介电常数透射电磁波,极化方向发生变化,磁场强度会由衰减.反射系数与透射系数的模型正演关系见表1,表2.

表1 金属异常体反射系数与透射系数的模型正演Table 1 Forward model of reflection coefficient and transmission coefficient of metal abnormal bodies

表2 空心异常体反射系数与透射系数的模型正演Table 2 Forward model of reflection coefficient and transmission coefficient of hollow abnormal bodies
3 结语
本文结合gprMax进行探地雷达正演模拟,探讨电磁波在地下介质中的运动路径和相位变化规律,通过gprMax对不同材质、不同深度、不同大小的地下异常体进行正演模拟并对比,就此算出关键反射界面的反射系数和投射系数.通过已有实验数据的介电常数进行仿真模拟地下金属异常和空洞,对比验证了其结果与经典电磁学中反射系数、投射系数以及相位变化的计算结果一致,证实了结合gprMax正演模拟的地下目标体解释的可行性.
