STEAM理念下的数学建模——以“最佳口感茶水问题”为例

龚舒倩 朱 哲 (浙江师范大学教师教育学院 321004)

近年来，越来越多的发达国家把STEAM教育作为国家战略发展的重要选择．在《中国教育现代化2035》提出加强拔尖创新人才的培养以及加大应用型、复合型、技术技能型人才的比重的现实要求下，STEAM作为整合培养实践型、创新型、综合型人才的教育理念[1]，在国内引起了一番研究热潮．数学是STEAM的基础学科，STEAM理念的融入为数学教育带来新的机遇与挑战．数学建模作为数学教育中最贴合STEAM理念的课程形式，是呈现STEAM理念的良好载体．数学建模能够为STEAM活动的开展提供着力点，STEAM理念也会为数学建模活动带来新思路与新方法，数学建模教学需要顺势而为，在新的时代背景下增添新的内涵．

1 STEAM理念进入数学教育

STEAM教育的理念可以概括为：以数学为基础，通过工程和艺术解读科学和技术．STEAM教育主要以基于项目的学习、问题的学习为主要教学方式，引导学生通过合作与实践，以学科整合的方式认识世界，以综合创新的形式改造世界，培养解决问题的创新能力[2]．数学是STEAM教育的基础学科，数学教育与STEAM教育的融合使二者相得益彰．一方面，数学在其他学科及实际生活中具有广泛的应用性，体验现实生活中的应用并以数学方式对现实世界的情况进行建模是有效STEAM教育的核心[3]．另一方面，STEAM教育同数学教育改革在理念上相契合．《普通高中数学课程标准(2017年版)》中指出：“高中数学课程强调数学与生活以及其他学科的联系，提升学生应用数学解决实际问题的能力．”而STEAM强调基于真实情境的跨学科学习将有助于数学教育的改革与发展[4]．

鉴于此，在数学教育中融入STEAM理念，探索数学教育与STEAM教育的融合模式是教育现代化背景下促进数学教育改革与发展的必由之路．

2 STEAM理念下的数学建模

STEAM作为一种理念支撑，切实落地于数学教育需要找到其相应的载体，这种载体既要能体现学科融合的特点，又要求能整合现有数学课程资源[5]．数学建模作为当下数学教育中最贴合STEAM理念的课程形式，是呈现STEAM理念的良好载体．数学建模是指对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题[6]，是实现数学学科的应用功能的重要中介和基本形式[7]．数学建模问题的背景通常取材于现实生活，对问题的分析不仅局限在数学上，还需要调动其他学科的知识或生活经验，以数学与现实问题及相关学科知识相融合的方式，确定影响问题的因素，进而做出合适的数学模型解决问题[8]．

数学建模和STEAM教育既有共通之处又相互独立．数学建模以数学学科为主导，体现的是数学知识和思维方法的广泛应用性，而STEAM教育不是将重点放在某个学科上，它体现的是跨学科思维、综合性学习．整体上STEAM教育包含的领域更广泛，不是所有STEAM活动都是建模活动，只是许多STEAM活动可能会经历建模过程，但在数学建模的过程中会涉及STEAM的各个方面[9]．STEAM教育和数学建模教学的融合，根据目标主体的不同可以归纳为两种模式(图1)：一是将数学建模活动作为STEAM教育的教学材料，在STEAM教育中融入数学建模思想，促使STEAM教育更加科学深入，目标是为STEAM教育服务；二是以STEAM理念指导数学建模教学，在数学建模过程中融入STEAM理念，使数学建模活动真正与实际生活以及其他学科紧密结合起来，目标是为数学建模活动服务，本文要研究的即是该问题．

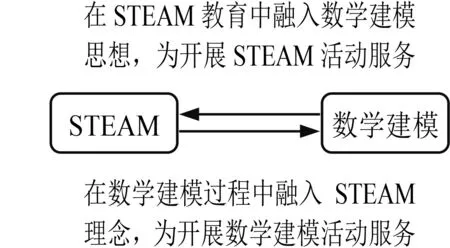
图1

STEAM理念的融入，为数学建模活动带来新思路与新方法．在理念上，从问题解决的单学科视角转变为多学科途径．STEAM理念下的数学建模能实现各学科知识内容、研究方法、思维方式和认知路径等的有效关联[10]．在方式上，从单一的理性分析转变为实践与分析相结合．让学生适时地走出纯思维的数学课堂，通过实践去接触实际问题，进一步引发他们的思考质疑和深入探究，反过来促进学生脑海中的数学建模思想更加完善[11]．

3 STEAM理念下的中学数学建模活动过程

基于以上对STEAM理念下数学建模的思考，笔者构建了STEAM理念下中学数学建模活动过程(图2)，总体分为选题开题、做题和结题三个阶段．

图2

第一阶段目的是让学生通过实践探究充分了解问题背景，运用跨学科思维综合分析把握问题本质，在选题开题的过程中渗透STEAM理念．首先，教师要根据选题内容精心设计教学活动，实现理论与实践相结合，课内和课外活动相结合，自主学习、小组合作、教师讲授等多种学习方式相结合．其次，引导学生运用跨学科思维分析问题，从多角度思考问题解决的策略，联系其他学科知识确定问题的影响因素．在进行教学设计时，教师要明确以下几点：①该问题涉及哪些学科知识？②这些知识是否基于学生已有知识经验？③这些知识是否有助于理解问题本质？最后，对现实的复杂情境作出合理假设，从开放性问题聚焦到条件更加明确的问题．根据学生的兴趣和经验可以提出不同角度的问题，根据学生的能力和水平可以提出不同难度的问题．该阶段结束后，要求学生撰写开题报告，在下一阶段汇报研究思路．

第二阶段是整个数学建模活动的中心和核心环节，目的是让学生在建立模型解决问题的过程中综合运用其他学科知识和生活经验提高思维的创造性和严谨性，在做题的过程中渗透STEAM理念．学生应经历对现实问题进行数学抽象、用数学语言表达问题、用数学方法构建模型解决问题的完整过程．在以小组合作的形式实践探究、收集数据的过程中，可能会涉及其他学科的知识内容以及实验操作，教师要对此加以复习、指导．结果的检验既要检验模型与实验数据的拟合程度，还要判断根据所得的模型推出的问题结论是否符合实际经验和其他学科的认知．

第三阶段是结题，目的是在总结反思、交流学习的过程中，引导学生再创造、提升各方面的素养．学生要完成结题报告，教师要组织结题答辩．结题报告可以采用多种形式和内容，形式上鼓励实践操作和使用信息技术，内容上提倡结合其他学科知识．在整个结题过程中，要以设计思维为导向，充分发挥学生的创新精神，设计思维不仅能够促进学习者反思以及对实践中经历的反思进行再反思，还能促进学习者应对解决真实世界中复杂问题的能力[12]，这一点与数学建模教学和STEAM教育的目标不谋而合．

总之，STEAM理念应贯穿数学建模全程，即“以STEAM理念分析数学建模问题，以STEAM理念指导数学建模过程，以STEAM理念总结数学建模活动”．

4 STEAM理念下的数学建模案例

基于STEAM理念下的数学建模活动过程，以人教A版《普通高中教科书·数学(必修)》第一册数学建模专题中的“最佳口感茶水问题”为例开发教学案例．

4.1 第一阶段：选题开题

(1)自主学习调研，了解问题背景

课前设置自主学习任务单，让学生分小组进行调查研究、自主学习，充分了解问题背景．任务单中明确要解决的问题，提供可学习的方式，如 图3所示．

图3

(2)跨学科思维分析，把握问题本质

课上请每个小组交流分享学习调研的结果．

生1：中华茶文化博大精深．根据制作工艺的不同，有六大茶类．

生2：水为茶之母，器为茶之父．泡一杯好茶除了茶叶，水和器具也很重要．

生3：看到茶艺师行云流水般的茶艺，感觉泡茶就是一项艺术．

师：那么如何才能泡出一杯好茶呢？哪些因素会影响茶水的口感？

引导学生从学习调研结果出发，运用发散性思维多角度思考．以下是教师的总结，将学生的回答归纳为茶叶、茶水、茶具、茶艺四类，结合其他学科的知识进行更深入的解释，帮助学生把握问题本质．

·茶叶

师：茶叶的可口程度和它内含的生化成分有关，主要是氨基酸和茶多酚的含量高低以及两者的比值关系．茶叶的制作工艺在很大程度上会影响茶叶的口感，通常觉得绿茶较为清爽，红茶较为甘醇，就是因为不同加工过程中茶多酚类物质氧化程度不同．发酵是茶叶加工的一种方式，茶叶在发酵过程中，因其自身氧化酶和微生物的作用，多酚类物质会转化成茶红素、茶黄素等[13]．因此，绿茶作为未发酵的茶叶种类，多酚类物质含量最高．

·茶水

师：《梅花草堂笔谈》言“茶性必发与水，八分之茶，遇十分之水，茶亦十分矣；八分之水，试十分之茶，茶只八分耳．”茶性的发挥需要合适的水，水质只是一方面，不同的茶叶对水的温度、水的比例都有要求．以鲜嫩的绿茶为例，茶与水比例为1∶50，水温通常在85 ℃左右，水温太高容易破坏茶中维生素C，咖啡碱容易析出，致使茶汤变黄，滋味较苦．除此以外，喝茶也讲究水温．我们的口腔、咽部等部位的粘膜都是柔嫩脆弱的，一般能承受50 ℃～60 ℃左右，喝过热的茶水容易破坏粘膜、诱发食道癌．

·茶具

不同的茶叶都有各自适宜的茶具，茶具的物理材质特性是茶具选择的一个重要因素．茶具的质地以密度来区分，密度不同，导热和散热系数也就不同，一般密度高的茶具，散热速度快，保温效果差．所以茶具的密度高，泡出的茶香清扬，密度低，泡出的茶香低沉．通常茶具材质密度排序为：玻璃>瓷器>陶器，因此用玻璃茶具冲泡绿茶比较好，瓷器冲泡红茶比较好，陶器如紫砂壶可以冲泡黑茶．

·茶艺

茶艺，萌芽于唐，发扬于宋，改革于明，极盛于清，是饮茶活动过程中形成的艺术文化现象．虽然茶艺师的手法、经验会在一定程度上影响茶水的口感，但是茶叶本身的品质难有较大改变．

(3)假设情境，聚焦问题

师：在前面的学习中了解到，茶水口感受很多因素影响，但是最重要的因素是茶叶类型、水温以及泡茶的时间．绿茶通常用85 ℃的水泡制，再等到茶水温度降至60 ℃饮用，茶水口感最佳．那么在25 ℃室温下，一杯刚泡好的茶水需要放置多长时间才能达到最佳饮用口感？请同学们就这一问题进行思考，小组讨论确定研究方案、撰写开题报告．

4.2 第二阶段：做题

(1)数学抽象，明确思路

组织开展开题交流活动，对该问题进行数学抽象，明确做题思路．

组1：用85 ℃的水泡制绿茶，每隔1 min测一次水温，等到60 ℃左右，就可以知道大致的时间．

师：如果想知道更加精确的时间怎么办？茶水温度变化是否有规律？

组2：先收集一些每隔一定时间的茶水温度数据，找到茶水温度随时间变化而变化的规律，据此计算茶水降至60 ℃时的时间．

师：什么数学模型可以刻画事物变化的规律?

生：函数．

师：明确思路是建立茶水温度随时间变化的函数模型，求出茶水从85 ℃降到60 ℃所需的时间．应当如何选择恰当的函数模型呢？

生：收集数据，作散点图，通过图象判断适用的函数模型．

(2)合作探究，收集数据

在开始收集数据之前，引导学生思考该实验需要控制的变量(茶叶类型、茶水比例、茶具等)．让学生以小组为单位，分工合作，进行茶水温度测量．由于该实验涉及水量、温度的测量，需带领学生复习量杯、温度计的使用方法．

材料：绿茶、电子秤、玻璃茶具、量杯、电热水壶、温度计、秒表等．

要求：先在茶具中投放3 g绿茶，再用量杯称量150 ml水，煮沸后待温度降至85 ℃时泡制绿茶，每隔一段时间测量茶水的温度并记录数据．(请1组学生每隔30 s测量茶水温度，直至水温趋于稳定，用该组数据留待检验模型)

(3)建立模型

各小组根据收集的数据，以时间为横轴、水温为纵轴作散点图，汇报所选择的函数模型．

组1：观察发现，茶水温度随时间流逝而逐渐变低，选择用k值为负的一次函数．

组2：我们测量的时间间隔更短，数据点分布更加密集．观察发现茶水温度不是线性降低的，先降得快后降得慢，选择用开口向上的二次函数．

组3：发现茶水温度随时间流逝而逐渐变低，先降得快后降得慢．并且根据经验，最后会接近于室温值，选择反比例型函数或指数型函数．

选择模型时应该看这个模型是否能客观地反映所要解决的问题的本质[14]．根据热交换原理向学生解释，在茶水降温的过程中为什么开始降得快后来降得慢，并且最后趋于稳定．因此，一次函数、二次函数都不符合这个特点，可以选择反比例型函数或指数型函数作模型假设．

师：根据散点图并联系实际，所求的函数图象在平面直角坐标系中应具有什么特点？

生：①与纵坐标轴有交点，②趋近于一个定值．

师：基于以上特点，如何作出你们的模型假设？

组2：选择指数型函数，假设函数模型y=kax+b．

(4)求解模型

可以用两种方法来求解模型．一是直接计算，各小组将各自的数据代入假设的解析式，用待定系数法求解，并通过计算残差平方和进行误差分析．二是利用软件，用Matlab或SPSS作拟合，用最小二乘法的原理得出该种模型下的最优函数．

(5)检验结果

首先根据实验数据进行检验，发现指数型函数拟合程度更好．其次，利用所求的指数型函数推出泡制一杯最佳口感茶水所需时间是7 min．然而根据实际经验，绿茶的冲泡时间一般不超过3 min，茶叶浸泡时间过长则茶汤苦涩，且内含物析出过多对人体有害．因此，还需要在所得的指数型函数的基础上继续修正模型．

(6)修正模型

通过视频展示茶艺师泡茶的过程，既要保证茶汤温度适宜又要防止茶叶久泡，可以选择在茶叶冲泡3 min后，将茶汤倒入公道杯中，待温度适宜再品茗．据此冲泡流程，茶汤在转入公道杯时，会有热量损失，因此可建立分段函数，在明晰能用指数型函数刻画茶水温度随时间变化的基础上，重新收集数据，修正模型．

(7)问题解决，模型推广

解决了25 ℃室温下泡制一杯最佳口感茶水所需时间的问题，进一步思考，尝试将建立的模型一般化，探究不同室温下泡制一杯最佳口感茶水所需的时间．

4.3 第三阶段：结题

要求学生课下撰写结题报告，总结反思这次数学建模活动．各小组根据各自的函数模型，设计泡一杯最佳口感茶水的步骤，为家人或朋友泡一杯最佳口感的茶，并录制视频．组织开展结题答辩和交流分享．

5 结语

STEAM理念的融入势必会给数学建模教学带来更多可探索的空间，数学建模活动能够更加深入地与其他学科和实际生活联系起来，促进学生的数学建模素养落地．本文基于课题学习的形式构建了一个STEAM理念下的数学建模活动模式，以STEAM理念贯穿数学建模活动全程，并据此开发了教学案例，以期为中学数学建模活动的开展提供参考．