“模型”少一点 “积累”多一层

陈建洲 李玉荣 (江苏省南京金陵中学河西分校 210019)

文[1]由一道几何试题引发深度思考，给出了9个问题的解题分析，其中对问题1—3的求解引发了笔者的进一步思考：为何要那样求解？有没有更自然、适切的解法？深度思考的意义何在？在此与作者商榷.

问题1如图1，在矩形ABCD中，CD=3，AD=4，在AD边上取点E，H，在AC上取点F，作正方形EFGH，连结AG，点E′是点E关于AG的对称点，AE′交BC于点P，则PC的长为.

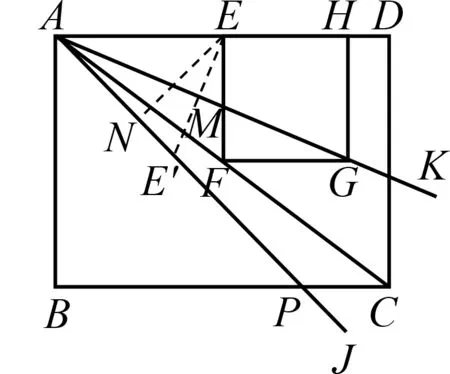
图1

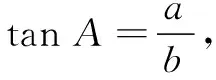
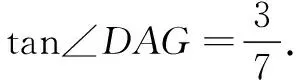
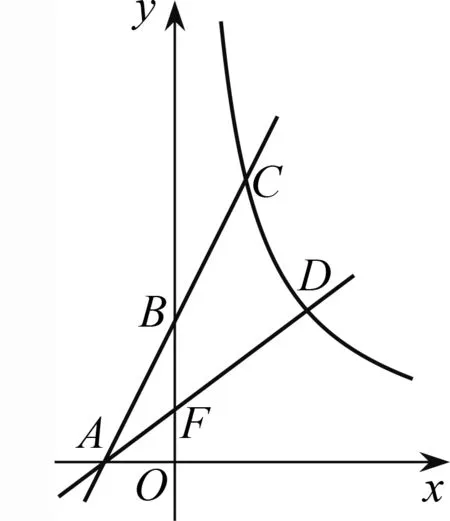
图1

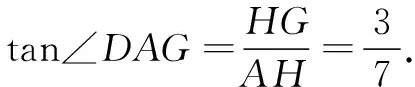
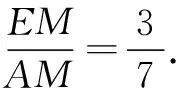
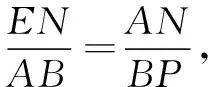
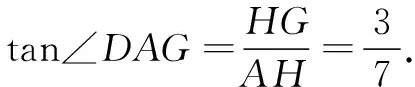
图2

又∠PAM=∠DAG=∠M，所以PA=PM，设PA=x，则BP=7-x.

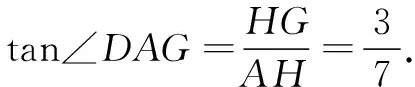
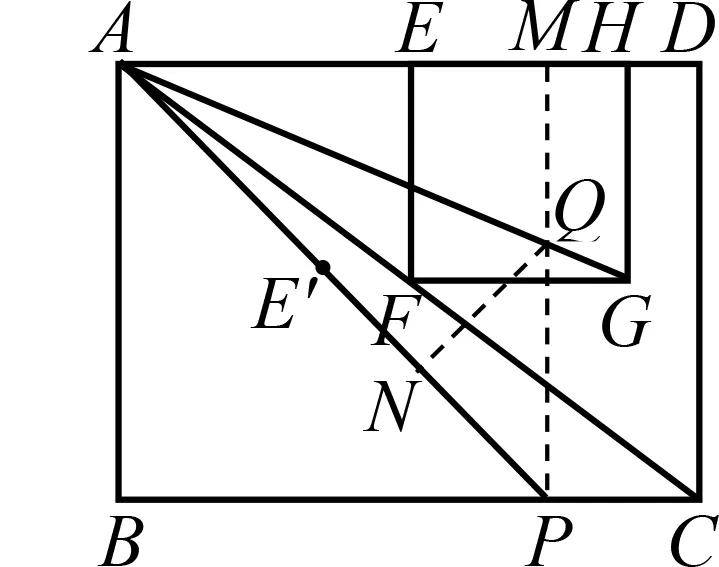
图3

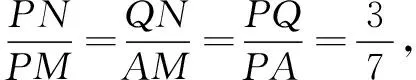
解法4如图4，延长GF交AB于点M，交AP于点N，则∠NAG=∠HAG=∠AGN，所以NA=NG.

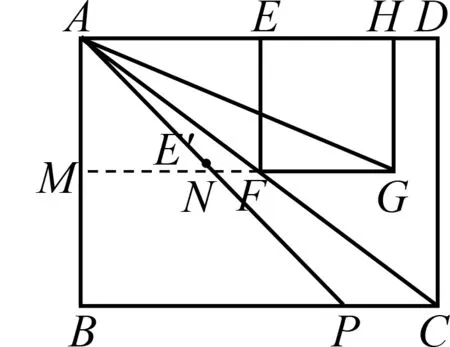
图4

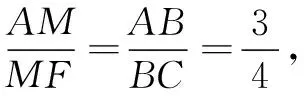
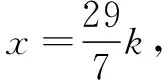
评注 解法1—4添加的都是朴实的辅助线，构造出“角平分线+平行线=等腰三角形”等与角平分线有关联的基本图形，使用了面积法、勾股定理、相似三角形等基本计算工具，贴近学生思维发展区，解法自然、适切.

问题2如图5，正方形ABCD中，AB=6，E是BC边中点，将△ABE沿AE对折，使得点B与点F重合，AF与对角线BD交于点G，求线段GF的长．

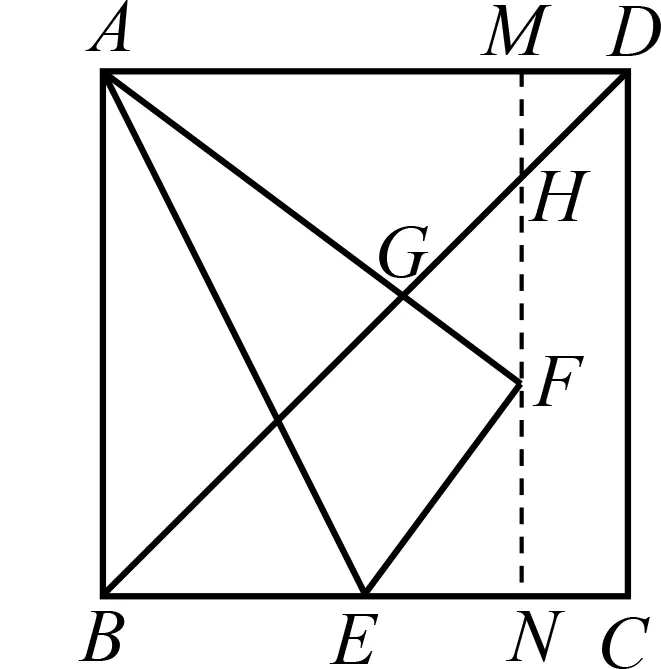
图5

分析 此题文[1]是利用之前探究的结论求解的，笔者以为作为解答题显然不妥.有更自然的求解方法吗？要求线段GF的长，只需求线段AG的长，需借助△AGB或△AGD求解，但条件暂时不足．注意到∠AFE=90°，于是有两个基本思路：一是构造“一线三等角型”相似三角形；二是构造“双垂直共角型”相似三角形，最后借助“X型”相似三角形求解.

解法1如图5，过点F作MN⊥AD于点M，交BC于点N，则MN=AB=6，AM=BN.

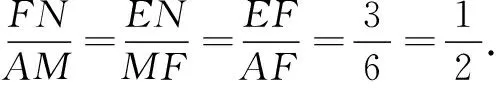
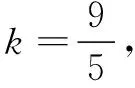
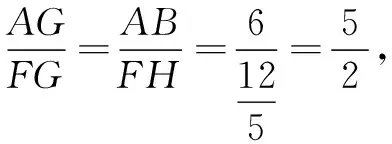
解法2如图6，延长AF,BC交于点H.

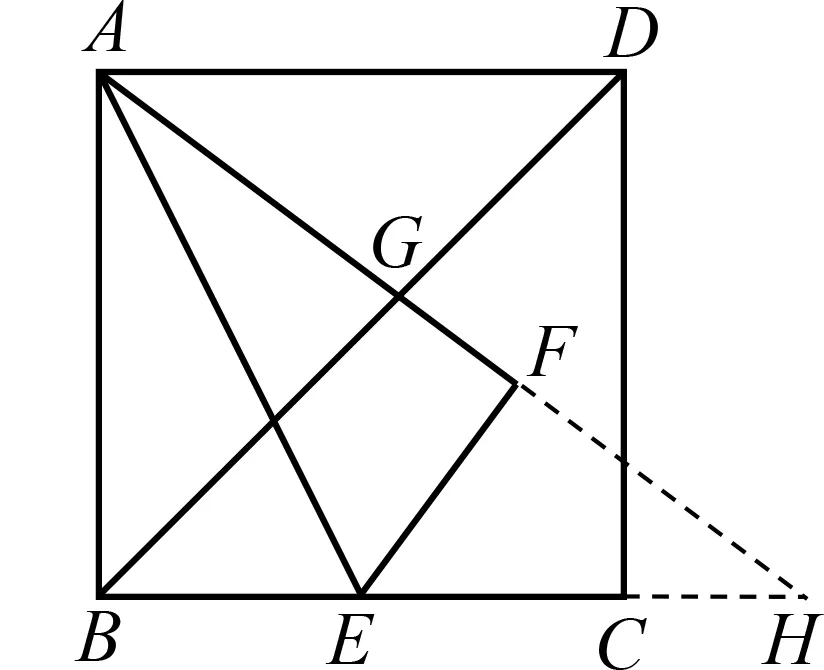
图6

设FH=k，则BH=2k，EH=2k-3，AH=6+k，所以6+k=2(2k-3)，解得k=4，所以AH=10，BH=8.

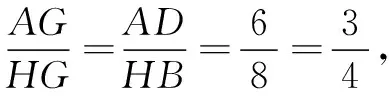
解法3如图7，延长AF交DC于点H，连结CF.

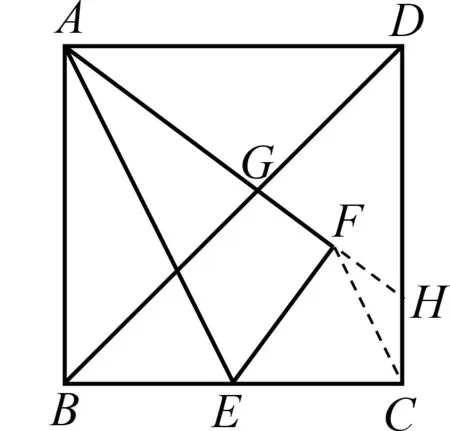
图7

因为EF=BE=EC，所以∠EFC=∠ECF，可得∠HFC=∠HCF，所以CH=FH.

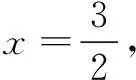
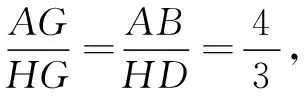
解法4[2]如图8，延长AE,DC交于点H，延长AF交DC于点M.

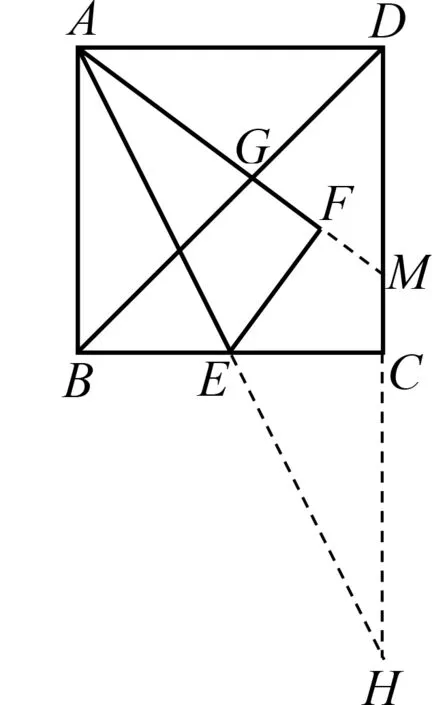
图8

易证△ABE≌△HCE，可得CH=AB=6，DH=12，∠BAE=∠EHC=∠HAM，所以AM=HM.

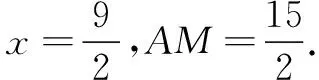
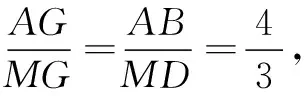
评注 笔者分别给出了问题1、问题2的4种解法，或许还有更多的解法可以探索，这不远比套“公式”求解更能启迪思维？

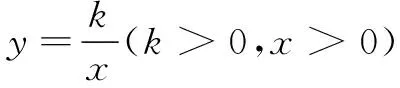
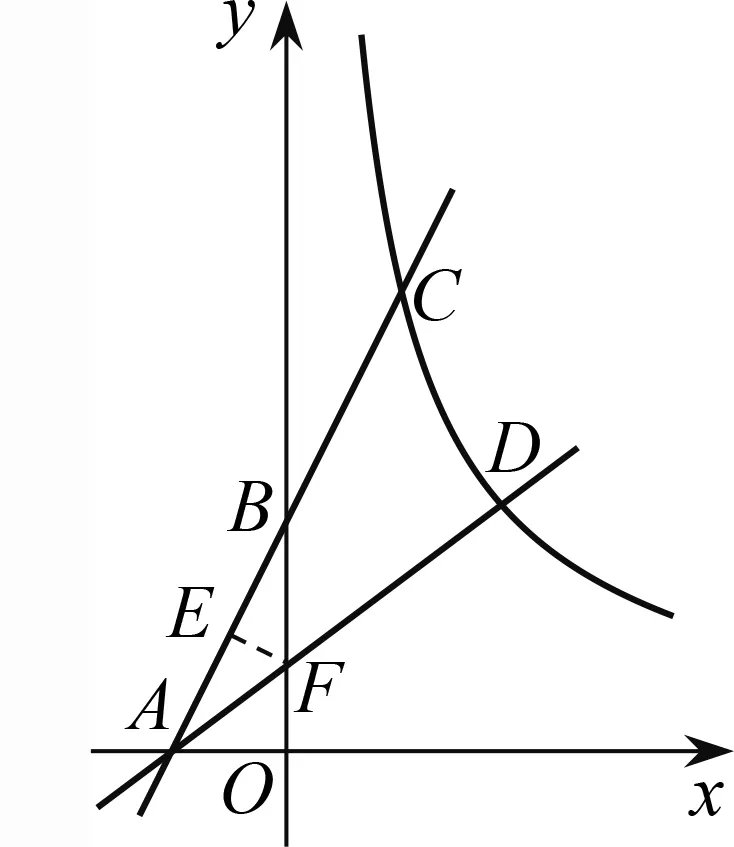
图9

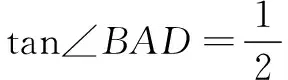
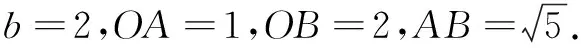
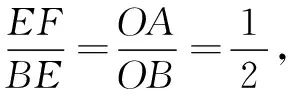
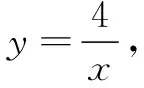
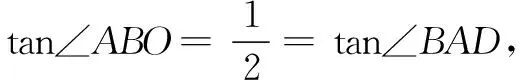
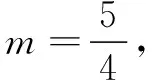
评注 这个解法无需添加辅助线，更无需套什么“公式”或“模型”，独具匠心.

不知从何时起，应对考试的“模型”充斥数学课堂教学，如“猪蹄”模型、“手拉手”模型、“12345”模型……让人眼花缭乱，教学年岁较长的教师甚至闻所未闻、莫名其妙.《义务教育数学课程标准(2011年版)》明确指出：“课程内容的组织要重视过程，处理好过程与结果的关系.”基于此理念，曾经耳熟能详的射影定理、相交弦定理、垂径定理等重要定理在教材上都已删去，那我们还有什么理由去编制所谓的模型(充其量也只能算基本图形)让学生去记忆、套用？解题是数学教师的最常见活动，学生学习数学更离不开解题，建立数学模型，对模型进行分析、求解，最终达到解决问题的目的无可厚非，甚至极为重要，但模型不能泛化，数学解题不能依赖并不常用的所谓“模型”或“结论”，更不宜在初中解题教学中大肆渲染一些远离教材的“模型”甚至是超标的内容，美其名曰“拓展延伸”，实际上是加重了学生的学业负担.泛化的模型等同于“拿来主义”：拿现成的“模型”去解难度大、思维含量高的数学题，表面上看解题过程简化了，但失去的是更有价值的数学思维，实在得不偿失.解题方法的教学理应遵循教材知识，执行课程标准，探寻贴近学生的发展区的自然解法，机械的“模型”或“结论”慎教、慎用，着力点应是强化过程性教学，让学生更多地思考、探究，体验获取知识的乐趣，促进数学思维能力的提升，增效减负才能真正落到实处.

完稿之余，恰好看到广东省2021年中考数学试卷第23题：

如图11，边长为1的正方形ABCD中，点E为AD的中点．连结BE，将△ABE沿BE折叠得到△FBE，BF交AC于点G，求CG的长．

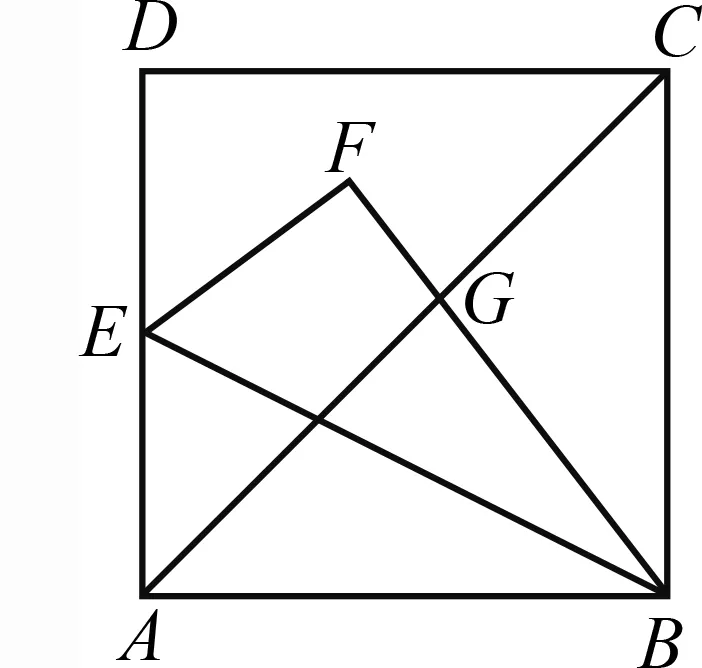
图11

此题与问题2极为相似，考生该用什么样的思路来求解呢？读者自有分辨．