风、浪作用下海上风机单桩结构时域动力响应分析

王 衔，邱 松，陈 涛，顾祥林

（1.中交第三航务工程局有限公司，上海 200032；2.同济大学工程结构服役性能演化与控制教育部重点实验室，上海 200092）

0 引 言

风能作为一种清洁能源，是21世纪用来降低对化石燃料的依赖性的重要资源。我国具有丰富的近海风力资源，国家在《能源发展“十三五”规划》［1］中指出，要积极开发海上风电，推动海上风电技术的进步和商业化运营，发展7～10 MW级风电机组。近年来，随着装机容量的不断增大，风机叶轮的半径和重量持续增加，对基础支撑结构的安全性提出了更高的要求。海上风电支撑结构在使用寿命周期内需承受高达约109次风、浪荷载的作用［2］，因此保证其疲劳性能满足要求尤为重要。

单桩支撑结构最早由荷兰莱利（NL）公司于1994年提出，截至2020年底，采用单桩支撑结构形式的海上风电基础占整个欧洲所有已装机的海上风电基础的81.2%［3-4］。这种适用于浅水海域且工艺相对成熟的支撑结构也是我国海上风电事业未来发展的首选。单桩与上部结构连接的主要方式是灌浆连接，其技术原理是通过向内外钢管间的环形间隙内填充高性能灌浆料，连接直径不同的过渡段与钢管桩。由于结构具有细长性，单桩支撑结构中的灌浆连接段主要承受反复弯矩的作用。本文结合广东某地的场地条件和实测风、浪数据，对某5 MW风机单桩支撑结构所受风、浪荷载进行模拟，并进行时域动力响应分析，从而提取出灌浆连接段的荷载边界条件时程，为进一步分析海上风机灌浆连接段的疲劳性能奠定基础［5］。

1 某5 MW风机单桩支撑结构动力响应模型的建立

某5 MW海上风机单桩支撑结构的设计参数见表1，结构示意图及实际场地条件见图1。

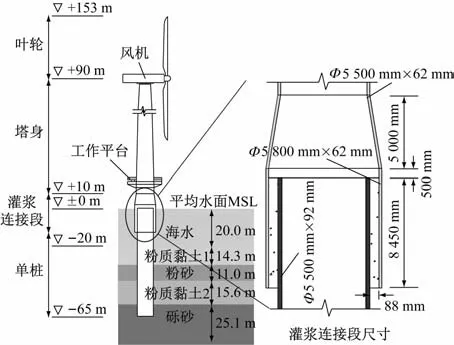
图1 某5 MW风机单桩支撑结构及实际场地条件

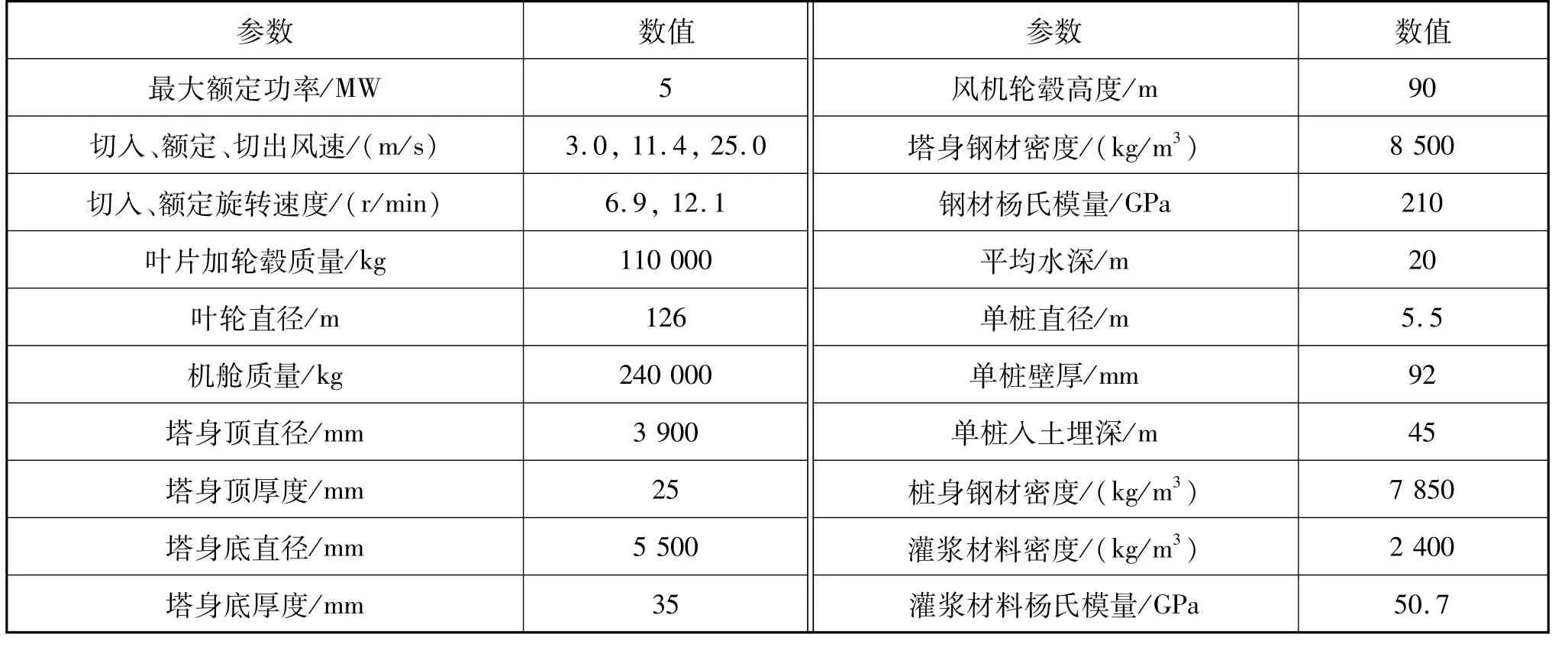
表1 某5 MW海上风机单桩结构的设计参数

1.1 桩-土相互作用的等效非线性弹簧

在将海上风机单桩支撑结构的单桩打入海床时，需考虑桩体与土壤（简称“桩-土”）的相互作用，尤其是桩体侧向位移下的土体对单桩的作用。挪威船级社（Det Norske Veritas，DNV）报告［6］指出，若单桩底部简单地按固接考虑，最多可能使结构基频产生20%的误差。

对于桩-土的相互作用，文献［7］提出采用非线性弹簧矩阵进行等效。图2为桩-土相互作用等效弹簧示意图，在桩顶施加水平力Fh和水平弯矩Mr之后，桩顶产生了水平方向的位移uh和转角θr，施加的荷载与位移之间的关系可用非线性等效弹簧矩阵表示，即

图2 桩-土相互作用等效弹簧示意图

由于对称性，本文采用ABAQUS软件建立桩-土相互作用区域的有限元半模型，见图3。土体边界半径为单桩直径的10倍，模型总厚度在桩体长度的基础上向下延伸4倍单桩直径，由此降低非无限大土体边界条件带来的影响。考虑到模型中土体的杨氏模量远小于单桩钢材，变形以土体为主，钢材的材料采用理想弹塑性材料即可。土体可根据其类别（砂土或黏土）的不同采用不同的材料模型。对于砂土，根据摩尔-库伦破坏准则，在ABAQUS软件中需输入其杨氏模量、泊松比、摩擦角、剪胀角、黏结强度和对应的绝对应变等参数。对于黏土，根据Tresca破坏准则，在ABAQUS软件中需输入其杨氏模量、泊松比、屈服强度和对应的塑性应变等参数。

图3 桩-土相互作用有限元半模型

土体和桩体都采用8节点实体减缩积分单元（C3D8R）模拟。土体的环向单元均匀分布，径向单元中间密两侧疏。上下层土体的环向网格和径向网格都应对齐，厚度方向的单元大小也应保持一致，但超过桩体长度的下部土体网格在厚度方向上可适当稀疏。单桩在厚度方向上采用四层单元，桩管与土体环向的网格节点应尽量对齐，单桩内外侧土体环向的单元节点也应尽量对齐。不同层土体之间的接触采用ABAQUS软件中的“tie”连接完全耦合。砂土和黏土与单桩接触面之间的正向接触都采用“硬接触”，并允许接触面分离；切向接触虽然都遵照库伦摩擦准则，但砂土与桩体的摩擦因数为tan（2／3φ′），其中φ′为砂土的有效摩擦角，且不设置摩擦强度的上限值。同时，黏土与桩体的摩擦因数一般取为常数0.4，并设置摩擦强度的上限值为黏土的不排水剪切强度。

对于土体的边界条件：底层土体底面采用固接约束；圆弧面上约束2个水平方向位移和沿竖直轴的转角；所有土层和单桩的对称面都施加对称面约束。同时，在桩顶截面形心位置处设置参考点，将该参考点与桩顶截面耦合。先进行重力荷载加载，再分别将水平力或水平弯矩荷载加载到参考点上，由此即可得到非线性等效弹簧矩阵，如式（1）所示。

1.2 某5 MW风机单桩支撑结构动力响应模型

海上风机单桩支撑结构属于细长结构，钢管的径厚比一般在1／100左右，因此很多学者都采用梁单元［8-9］或ANSYS有限元计算软件中的Pipe单元［10-11］模拟风机结构。由于不关注叶片的振动，很多文献［12-15］都采用塔顶集中质量的方式模拟风机叶片和机舱。本文采用ABAQUS软件中的梁单元和顶部集中质量的方式对风机单桩支撑结构进行简化。

此外，目前大多数学者在模拟风机单桩支撑结构时都未考虑对灌浆连接段进行模拟。然而，灌浆连接段处的局部刚度发生变化会对单桩支撑结构的动力特性产生影响。本文采用ILIOPOULOS等［16］提出的按比例分配法将灌浆连接段拟合成一种匀质材料的方法，根据3种材料的体积占比对密度、弹模和泊松比进行加权平均，采用均一化材料梁单元进行模拟。在考虑第1.1节所述桩-土相互作用等效弹簧约束之后，得到简化的单桩支撑结构动力响应模型见图4。对该模型和不考虑桩-土相互作用而直接固接的其他同类模型进行模态分析，得到标准振型和振型频率分别见图5和表2。通过比较可知，忽略桩-土的相互作用会对单桩结构的基频产生约6.3%的误差，会对结构的二阶频率产生约35%的误差，由此可见，考虑桩-土相互作用是很重要的。

图4 风机单桩支撑结构动力响应模型

图5 风机单桩支撑结构标准化振型模态

表2 某5 MW海上风机单桩结构振型频率

文献［17］给出了海上风机结构中阻尼的来源，包括材料本身的阻尼、土体阻尼、水动力阻尼和风机运行的气动阻尼。气动阻尼作为对风机结构的影响最大的“阻尼作用”，其大小由风速和风机翼型等因素决定。考虑到该阻尼的复杂性，本文参照文献［18］和文献［19］将静止的单桩支撑风机结构的阻尼比取为1%，参照文献［17］、文献［18］和文献［20］将考虑气动阻尼的单桩支撑风机结构的总阻尼比取为5%。

2 单桩支撑结构风、浪荷载模拟

处在海洋环境中的风机单桩支撑结构会受到腐蚀、闪电、船舶撞击、地震、浮冰和洋流等因素的影响，但文献［21］指出，单桩风机受到的荷载主要来自风对塔身的作用、风机的气动作用和波浪对单桩的作用，因此本文只考虑这3种作用。同时，假定风荷载与浪荷载作用在同一方向上，且风对塔身的作用和波浪对基础结构的作用在高度10 m以下的分段内均匀分布，积分之后集中作用在10 m分段的中点处，见图6。

图6 风机单桩支撑结构风、浪荷载简化示意图

2.1 广东省某地测风数据及风速、波高联合分布

下面给出广东省某沿海区域的测风塔和水文气象站测量得到的实际风速、海浪有效波高Hs和有效周期Ts等数据。测风塔风速测量时段为2016年1月1日00：00—2016年12月31日23：00；海洋站波浪测量时段为2016年3月1日—2017年2月28日。

由测风塔得到的年平均空气密度为1.175 kg／m3；下文风廓线理论式中的粗糙区长度z0＝6.02×10－6m。风机轮毂高度90 m处平均风速的长期分布经过拟合，符合双参数的Weibull分布，其概率密度函数为

式（2）中：β为尺度参数，其值为8.9 m／s；α为形状参数，其值为2.67。

结合海洋站的观测数据，实际风、浪的年观测数据共对应385种工况，其中：风速小于风机切入风速（3 m／s）的工况共有37种，概率总和约为5.32%；风速超过3 m／s的工况共有348种，概率总和约为94.50%，在这些工况下需计算风机运行产生的气动荷载。

2.2 风对塔身的荷载模拟

风场具有随机性，经典理论［22］指出，任意一点的风速都可视为平均风速项与脉动风速项的叠加。文献［6］认为，在10 min时间内，脉动风速服从高斯分布，且其紊流强度可认为是不变的。但是，长期来看，10 min时间内的平均风速服从双参数的Weibull分布。由于海上风机单桩支撑结构具有细长性，可将脉动风场简化为沿高度方向不同位置的单方向一维、多元平稳高斯过程。因此，风机塔身高度方向上任意一点水平方向的瞬时风速可表示为

式（3）中：vs（z）为高度z处水平方向的平均风速；vD（z，t）为高度z处t时刻水平方向的脉动风速。

对于水平方向的平均风速，文献［22］给出了不同高度处风速的风廓线理论，各高度处的平均速度可表示为

式（4）中：k为冯·卡门常数，常取为0.4［23］；z0为粗糙区长度；u*为剪切速度。

对于脉动风速的模拟，DNV规范［24］建议采用Kaimal谱模拟脉动风速，其表达式［22］为

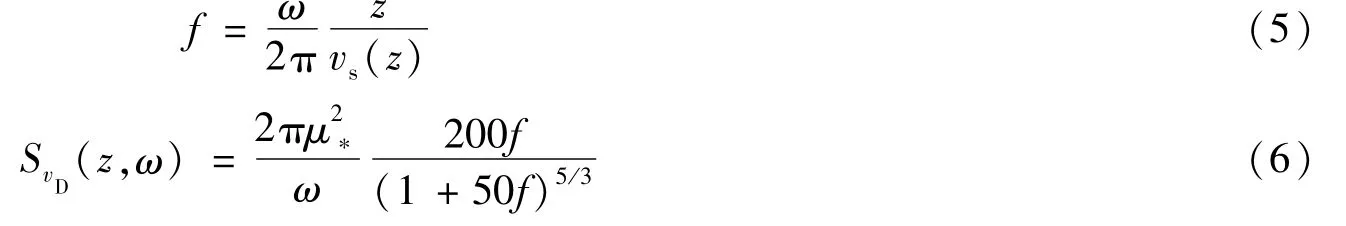
式（5）和式（6）中：f为Monin相似坐标参数；ω为风的圆频率。

对于不同高度处脉动风速之间的互功率谱，可采用Davenport互谱［25］，其表达式为

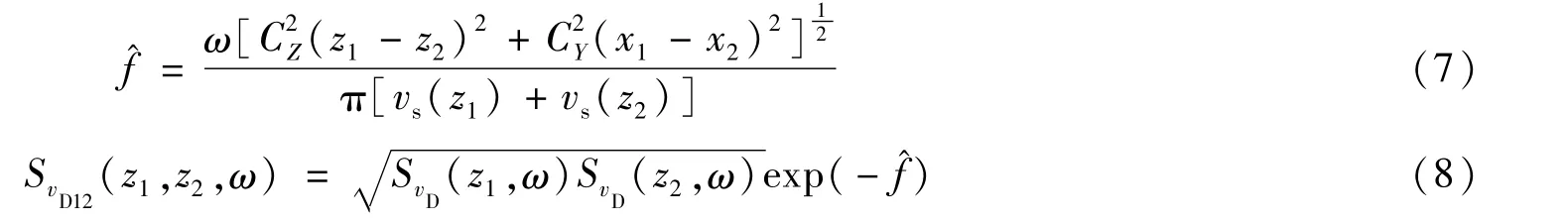
式（7）和式（8）中：CZ＝10；CY＝16［22］。由于忽略了水平方向的维度，本文无需考虑（x1－x2）项。

对于塔身微段面积dA内塔身的风荷载dF（z，t），同样由平均风荷载项dFs（z）和脉动项dFD（z，t）组成，即

式（10）中：CW为风荷载形状系数；ρ为空气密度；vs（z）为某点水平方向的平均风速。

对于塔身的风荷载的脉动项dFD（z，t），文献［26］将其功率谱写为

式（11）中：Svkvl为k点和l点的风功率谱矩阵；vsk和vsl分别为k点和l点的平均风速；ϕj（k）和ϕj（l）分别为第j阶单位振型下k点和l点的振幅；n为需考虑的振型阶数，对于海上风机单桩支撑结构，一般只需考虑第一阶弯曲振型即可满足精度要求。最后，结合风对塔身的荷载的功率谱矩阵SFkFl和文献［27］提出的改进的多元平稳随机过程谱表达法即可模拟得到风对塔身的荷载时程，见图7。采用相同的方法也可模拟风速沿塔身的时程，对模拟得到的风速时程进行傅里叶变换，将得到的模拟谱与目标Kaimal风谱相对比（见图8），由此即可证明模拟程序的正确性。

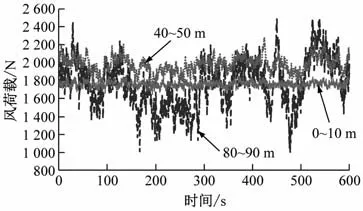
图7 沿塔身不同高度处的风荷载模拟结果

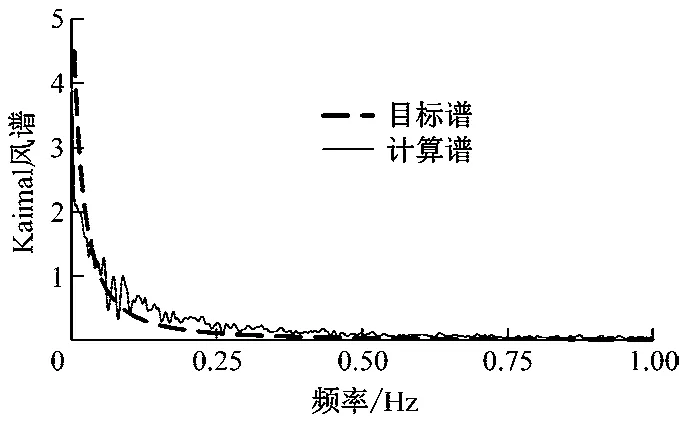
图8 Kaimal风谱模拟结果对比

2.3 风机运行气动荷载——叶素动量理论

目前可用来计算风机运行气动荷载的理论主要有叶素动量理论、涡旋理论、广义制动盘理论和纳维-斯托克斯解法等，其中叶素动量理论较为简易，不依赖专业的分析软件，应用最为广泛。结合经典文献［28］，对叶素动量理论进行相关编程，在此不再赘述。编程中使用的5 MW标准风机是美国国家可再生能源实验室（National Renewable Energy Laboratory，NREL）在2009年的报告［19］中提出的，其详细参数可参见该报告。

风机推力荷载时程模拟结果见图9。为验证程序的正确性，采用文献［19］中给出的标准风机扭矩与风速的关系曲线同模拟结果相对比，结果见图10。从图10中可看出，模拟结果良好，验证了叶素动量理论程序的正确性。

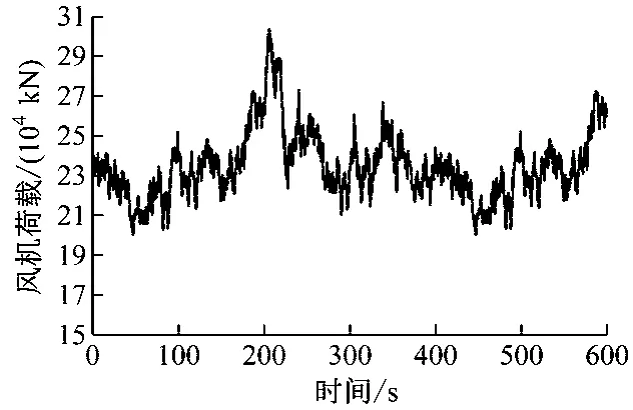
图9 风机推力荷载时程模拟结果

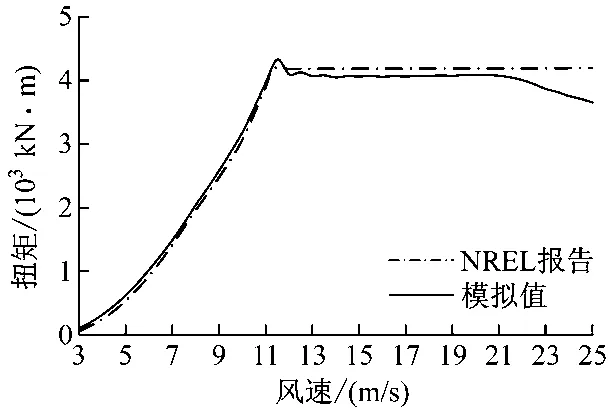
图10 风机扭矩与风速关系模拟结果

2.4 波浪荷载模拟

本文采用B-M海浪谱对海面波面高程η（x，t）进行模拟，该波浪谱由Bretschneider于1959年提出，后由日本学者Mitsuyasu（恒光易）［29］进行了改进，其表达式为

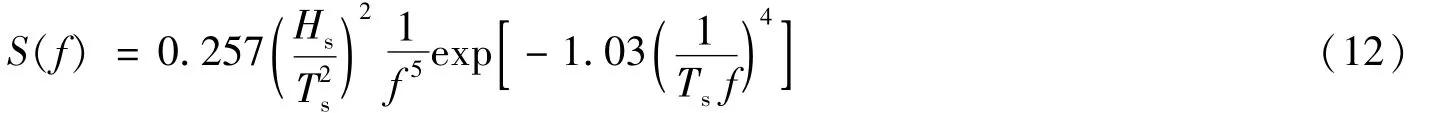
式（12）中：Hs和Ts分别为海浪的有效波高和有效周期。

采用一维平稳随机过程的谱表达法可得到海面波面高程的时程η（x，t），采用线性波浪理论可建立η（x，t）与任意深度z处波浪内的水质点的速度水平分量vx和加速度水平分量ax的关系，即

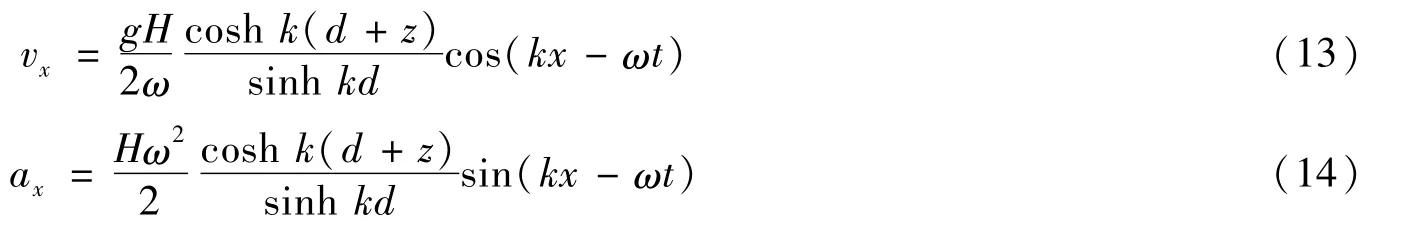
式（13）和式（14）中：t为时间；k为波数；ω为圆频率；g为重力加速度；d为水深。

波浪对单桩的作用力可采用Morison波浪力方程［30］表示，该方程是由Morison于1950年提出的半经验半理论公式，认为波浪对柱体的作用主要是黏滞效应和附加质量效应，因此可将波浪力分为同速度的平方成正比的阻力项和同加速度成正比的惯性力项，单位长度圆柱体上的波浪力F为

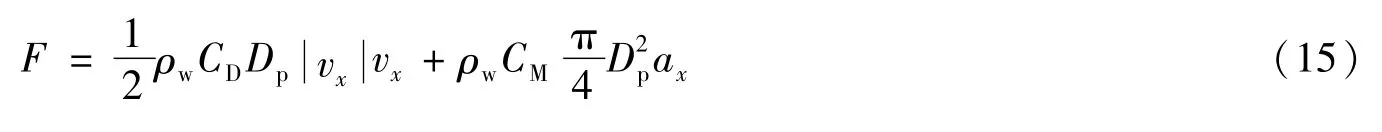
式（15）中：vx和ax分别为水质点的水平速度分量和水平加速度分量；ρw为波浪的密度；Dp为圆柱体直径；CD为拖曳力系数；CM为惯性力系数。德国劳氏船级社规范［31］附录4.H给出了CD和CM的取值，当波浪的雷诺数小于2×105时，对于光滑的圆柱体，可取CD＝1.2，CM＝1.0。

塔身不同高度处的波浪荷载模拟结果见图11。对模拟得到的海面波面高程时程进行傅里叶变换，得到的模拟谱与目标B-M海浪谱对比见图12，由此可证明模拟程序的正确性。

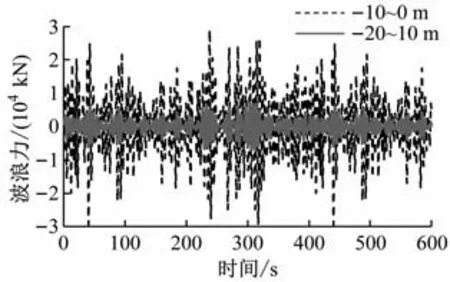
图11 塔身不同高度处的波浪荷载模拟结果

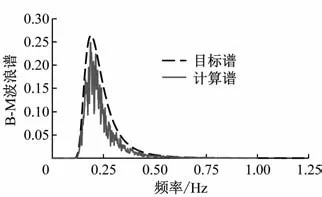
图12 B-M波浪谱模拟结果对比

3 单桩支撑结构时域动力响应分析

对第2.2～2.4节所述风、浪荷载模拟程序进行汇总，并将所有工况信息写入Excel文件中，采用MATLAB软件自动读取Excel文件的功能依次读取所有工况下的平均风速、有效波高、有效周期和发生概率等参数，自动生成风、浪荷载时程汇总文件，见表3。本文在模拟风、浪荷载时，取时间间隔为0.2 s，模拟总时长为10 min。当风速低于3 m／s时（即2.1节中的37种风机不工作工况），汇总文件中没有气动荷载一列。

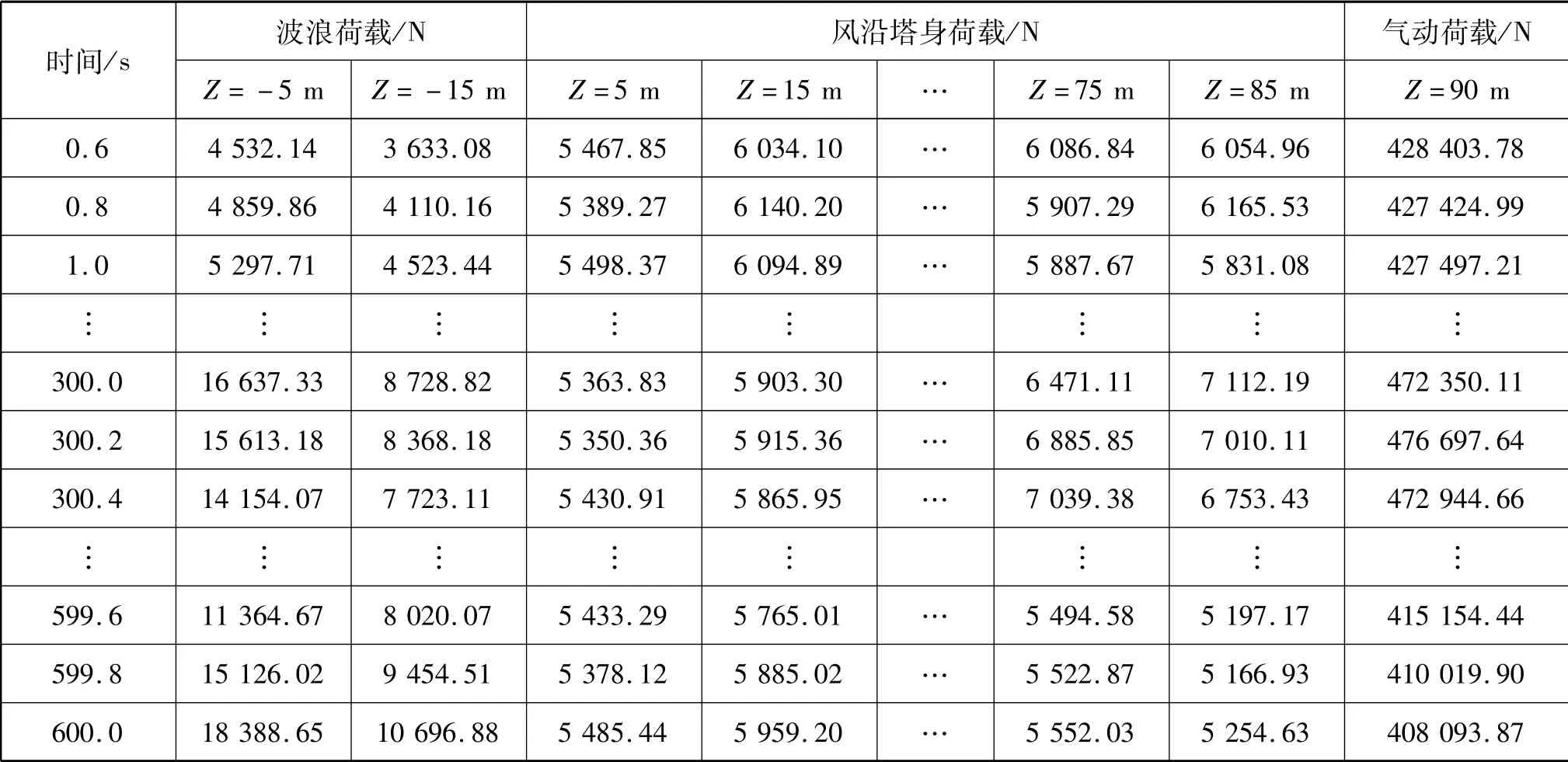
表3 模拟得到的风、浪荷载时程汇总

在不同工况下进行时域动力响应分析时只有输入的荷载不同，而单桩支撑结构的动力响应模型的阻尼比只在风机不运行（37种工况）和风机运行（348种工况）2种状态下不同。为在ABAQUS软件中实现批量计算，运用Python语言编写相应程序，自动读取表3中的数据，并将其修改写入“inp”文件中。对于各工况，按其风速判断风机是否处于工作状态，修改结构的阻尼系数。

将批量修改的“inp”文件批量提交给ABAQUS Command，等待逐个自动计算，在酷睿i5处理器、内存24G的硬件条件下，每种工况的平均计算耗时约为12 000 s。

然而，通过对提取的灌浆连接段荷载边界条件进行整理，发现一些问题。本文采用第一步施加重力荷载，第二步施加风、浪随机动力荷载的加载方式。当第二步开始时，风浪荷载相当于突加荷载，结构在该突加荷载下会产生振荡的过程，结构的位移和内力出现突增现象，且单桩支撑结构的总阻尼比较小，该振荡并不能很快衰减。该振荡过程可通过风机运行和不运行2种工况下的灌浆连接段顶部轴力时程曲线（见图13和图14）。图13给出了风机不运行工况下灌浆连接段顶部的轴力时程曲线，此时单桩风机结构的阻尼比为0.01。从图13中可看出，振荡过程约持续300 s，在300 s之后轴力趋于稳定。图14给出了风机运行工况下灌浆连接段顶部的轴力时程曲线，此时单桩风机结构的阻尼比为0.05。从图14中可看出，振荡过程约持续120 s，在120 s之后轴力和水平弯矩趋于稳定。因此，在后续对灌浆连接段的疲劳性能进行评估时，采用的荷载边界条件数据在风机不运行工况下取时程分析的后300 s范畴，在风机运行工况下取时程分析的后480 s范畴。

图13 风机不运行工况下的灌浆连接段顶部轴力时程曲线

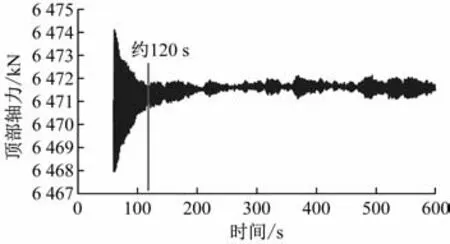
图14 风机运行工况下的灌浆连接段顶部轴力时程曲线

此外，编写相应的Python程序，实现对所有工况下的计算结果文件（灌浆连接段荷载边界条件）的自动提取，为进一步对灌浆连接段进行疲劳分析奠定基础。

4 结 语

本文结合广东某地的场地条件和实测风、浪数据，综合运用Kaimal与Davenport风谱、风机叶素动量理论、B-M波浪谱、线性波浪理论和Morrison波浪力理论，对某5 MW单桩风机支撑结构所受风、浪荷载进行了模拟，并对单桩结构进行了时域动力响应分析，从而提取出灌浆连接段的荷载边界条件时程，为进一步对灌浆连接段的疲劳性能进行分析奠定基础。单桩支撑结构动力响应模型综合考虑了桩-土相互作用的等效弹簧和灌浆连接段部分刚度的匀质化。研究发现，忽略桩-土的相互作用会对单桩结构的基频产生约6.3%的误差。同时，考虑风机气动阻尼的影响之后，风机在运行工况下的动力响应进入稳态阶段的时长相比在停机工况下更短。