超大型集装箱船水动力时域分析

陈明高，李雪剑，付泽坤，李海洲，米 洁

（江南造船（集团）有限公司，上海 201913）

0 引 言

万箱以上的超大型集装箱船是目前国内船舶行业设计开发的重点船型之一，其结构设计与常规集装箱船有所不同［1］。不同集装箱船因自身特点不同，在强度评估方面有不同的要求：对于巴拿马型船，或者是船级社和船舶设计单位已有相关经验的普通设计船型而言，做规格规范计算及三舱段分析即可；对于大的集装箱船（船长L＞230 m）或创新设计船而言，要求做基于直接波浪载荷的全船有限元分析。三维频域理论中最常用的数值方法是格林函数法，目前应用最广泛的是三维自由表面格林函数法和Rankine源法。有航速问题一直是三维频域方法的难点。时域理论在处理非线性和瞬态问题方面具有优势。CLEMENT［2］提出用常微分方程替代无限积分的运算，并利用常微分方程的初边界条件，在基本解的基础上构造了计算求解时域格林函数的方法；朱传仁等［3］结合制表插值和求解常微分方程，计算了有航速情形下Wigly型船的运动响应。陈曦［4］利用高阶面元离散形式结合Rankine源格林函数计算了船舶兴波问题；许博方等［5］采用基于三维频域线性理论的波浪分析模块WADAM，对一艘集装箱船进行了波浪载荷计算和全船结构强度分析；唐卫军［6］采用三维时域Rankine源方法对大型集装箱船的六自由度运动和波浪载荷进行了计算。

1 相关理论分析

对于无航速的情况，若假设船舶摇荡为小量，则1阶不定常速度势ϕ（x，y，z，t）满足以下定解条件，即

式（1）～式（4）中：S0为船体的平均浸湿表面；vn为S0上点运动的法向速度；（t）为j模态的运动速度；nj为物体表面单位法线矢量在j向的投影。

为满足定解条件中的自由表面条件，使场内的速度势由该条件下的格林函数或其法向导数物面上的分布决定，需引进一个新的格林函数，即

式（5）～式（7）中：P（x，y，z）和Q（ξ，η，ζ）分别为域内任一场点和源点；r为场点与源点的距离；r′为场点与源点相对于静水面的映像点的距离；J0（kR）为零阶的第一类贝塞尔函数。不定常速度势时域内积分方程为

式（8）中，S0为物面；SF为自由液面。由于哈斯金特关系，只需考察物体运动的辐射势。同时，由物面条件得到ϕR的值不仅取决于物面形状，而且取决于物体的运动速度和加速度，并与运动历史有关。

式（9）中：ϕRI（P，t）为初始运动条件下产生的流体运动速度势；ϕRM（P，t）为物体运动引起的速度势。引入符号

式（10）和式（11）中：ψj（P）为单位速度脉冲运动引起的流动响应；为前一脉冲对后续流体运动的影响，体现了自由表面的记忆效应。

场内速度势由入射波势、辐射势和绕射势组成，根据线性伯努利方程求得流体动压力，建立时域内的船体运动方程，有

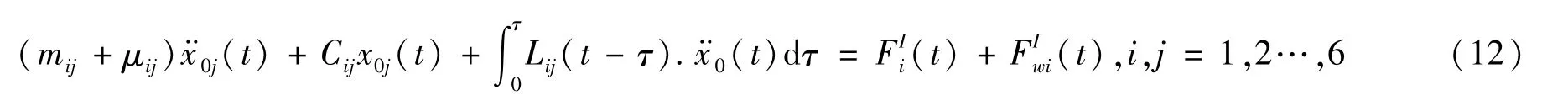
2 水动力计算

2.1 软件和模型

水动力计算采用挪威船级社（Det Norske Veritas，DNV）旗下的SESAM软件包进行。SESAM作为一款功能强大的商业通用有限元软件，可基于三维绕射理论，对船舶及海洋结构物进行水动力分析。该软件是由多种不同功能模块组合形成的大型软件包：利用子模块GeniE建立水动力计算模型；利用子模块WADAM和WASIM进行波浪载荷分析和响应计算；采用子模块POSTRESP进行后处理。本文先通过频域分析程序WADAM得到横摇阻尼系数，计算方法见2.2节。WADAM模型（见图1）是在GeniE模块中建立的平台湿表面面元模型，包含切片模型和舭龙骨模型。在时域分析中，由于计入了非线性恢复力和入射波力的影响，在计算时要不断地重新划分湿表面面元。WASIM时域分析模型见图2。

图1 WADAM模型

图2 WASIM时域分析模型

2.2 计算方法

由于势流理论的局限性，势流理论方法中的横摇阻尼事实上只计入了兴波阻尼，无法考虑黏性的影响和横摇时可能出现的流动分离和旋涡现象，因此若不加以修正，横摇运动的预报精度会很差。特别是当外界波浪激励频率接近横摇共振频率时，横摇运动的预报精度缺乏工程实用性。在横摇幅度不过大的情况下，兴波和摩擦引起的阻尼与横摇角速度的关系接近性线关系，而黏性引起的压阻尼与横摇速度的平方成正比。船舶横摇阻尼主要由B44W、B44L、B44F、B44E和B44APP等5部分组成，其中：B44W为波浪引起的兴波阻尼；B44L为由船体产生的上升力产生的阻尼；B44F为由船体表面摩擦引起的阻尼；B44E为由旋涡分离产生的阻尼；B44APP为由附属物（如舭龙骨、鳍）产生的阻尼。

精确确定阻尼是横摇研究中最困难的工作，最可靠的方法是进行实船或模型试验。TANAKA等［8］在试验数据的基础上研究了船体旋涡对横摇阻尼的影响。KATO［9］发现舭龙骨对横摇的影响与多种因素有关，如面积、宽度、雷诺数和吃水等。这些影响正比于舭龙骨平均速度的n次方，其中n由舭龙骨宽度、吃水、舭龙骨和船舶重心距离确定。在试验数据的基础上，分别计算这些影响系数，得到横摇阻力计算公式。

在设计初期，可用经验公式进行估计。船舶横摇阻尼与最大横摇角、波浪频率和航速等多种因素有关，其中最大横摇角通常需通过迭代计算得到。国际拖曳水池会议（International Towing Tank Conference，ITTC）在2011年给出了横摇阻尼数值计算的推荐方法［8］。

在计算过程中：B44F和B44E通过2D切片模型，按ITTC 2011年推荐的方法计算；B44APP通过对舭龙骨位置和角度沿船长积分得到；由于选择ITTC推荐的方法，由速度引起的船体上升阻尼B44L也可考虑在内。通过对横摇角进行长期预报，逐步确定最终的最大横摇角。具体计算方法如下：

1）针对每个浪向输入一个初始的最大横摇角θinput；

2）根据建立的水动力模型进行水动力计算；

3）对最大横摇角进行长期预报，得到一个新的横摇角θupdated，超越概率为10－8；

4）若θupdated接近θinput，则停止计算，否则设置一个新的θinput等于θinput与θupdated的平均值，重新回到步骤1）进行计算。

最终通过水动力计算和长期预报确定的各浪向角下的船舶最大横摇角度见表1。

表1 各浪向角下的船舶最大横摇角

2.3 横摇阻尼系数计算结果

表2为浪向角为90°时不同航速下的横摇阻尼系数，其单位均为RO·VOL·L·SQRT（G·L），其中：RO为水密度，kg／m3；G为重力加速度，N／kg；L为船的特征长度，m；VOL为排水量，m3。从表2中可看出，旋涡分离产生的横摇阻尼随航速的增加而减小的速度很快，其他因素的横摇阻尼系数变化不大。

表2 浪角为90°时不同航速下的横摇阻尼系数

2.4 时域计算结果

本文以一艘超大型集装箱船为例进行分析，该船总长约为360 m，船宽为48 m，设计航速为25 kn。计算选取的航速分别为0 kn、5 kn、10 kn、15 kn、20 kn和25 kn。选取的波浪周期范围为3～25 s。计算集装箱船在6个航速、7个浪向角下的六自由度运动响应。当航速较高时，船舶的运动姿态变化比较大，此时回复力会变化，且姿态变化较大会对湿表面的变化产生很大影响，非线性时域方法能计入瞬时湿表面变化对非线性恢复力和入射波力项的影响。图3和图4给出了横浪状态下航速为25 kn时的船舶六自由度运动响应时历曲线。从图3和图4中可看出：纵向运动幅度较小；横荡、升沉和横摇运动幅度较大。此时产生较大的横向和垂向运动加速度，波浪对船体外板产生较大的波浪载荷。完成时域求解之后，可通过傅里叶变换将时域结果转化为频域结果。通过对频域结果进行长期预报，可进一步考察不同航速、不同浪向角下的横摇响应值，结果见表3。

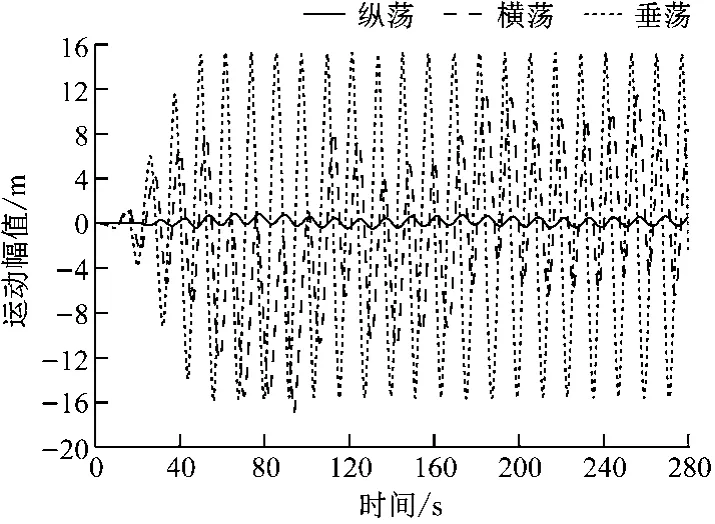
图3 船舶纵荡、横荡和垂荡时历曲线

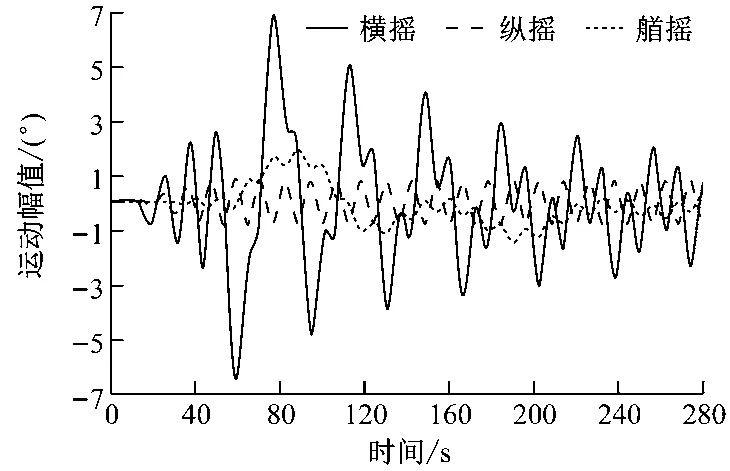
图4 船舶横摇、纵摇和艏摇时历曲线

表3 不同航速、不同浪向角下的横摇响应值

图5和图6为船舶六自由度运动响应曲线。由图5和图6可知：纵荡的航速效应最为明显；除了垂荡，其余运动响应的航速效应都不可忽视。

图5 船舶纵荡、横荡和垂荡响应曲线

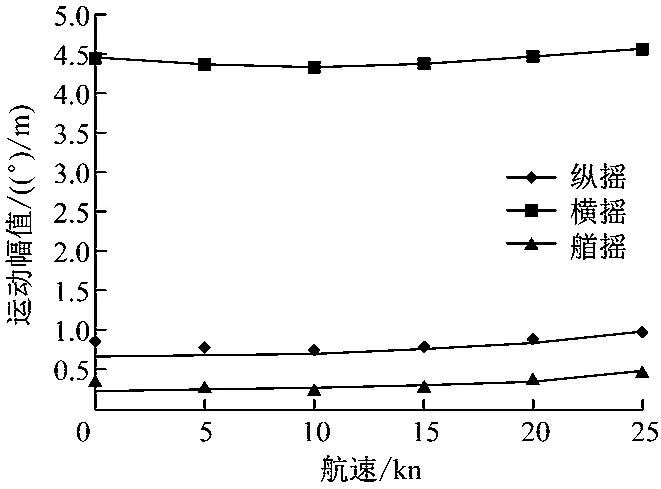
图6 船舶纵摇、横摇和艏摇响应曲线

图7为垂向剪力响应曲线。由图7可知：船中剖面处的垂向剪力随航速的增加而增加，航速效应明显。

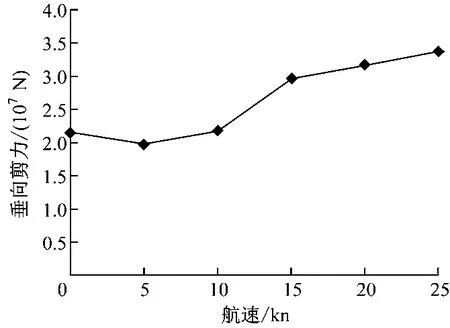
图7 船舶垂向剪力响应曲线

3 结 语

本文研究了横摇阻尼计算和航速对黏性阻尼的影响；同时，采用时域分析方法详细计算了不同航速、不同浪向角下的船体运动响应，以及船体剖面垂向剪力、垂向弯矩和扭转弯矩。结果表明：除了垂荡的航速效应不明显，其余航速的航速效应均不可忽略；纵荡航速效应尤为明显；垂向弯矩随航速的增加而增加较多。

本文的研究对船舶水动力分析及船体波浪载荷计算有一定的参考价值。本文未考察非线性波浪对集装箱船运动和波浪载荷的影响，由于集装箱船具有船首外飘的特点，船舶大幅度运动伴随着底部砰击引起的非线性载荷，这些内容有待进一步深化研究。