深层2D反卷积神经网络的序列推荐算法

李昆仑,孙瑞刚,王 珺

(河北大学 电子信息工程学院,河北 保定071000)

1 引 言

随着互联网以及电子商务的快速发展,互联网上的信息量爆发式增长,用户难以从过载的数据量中找到有用的信息,而个性化推荐系统是解决这个问题的有效途径之一.传统的推荐算法如基于内容的推荐算法,协同过滤推荐算法等已经在推荐系统领域取得了较好的效果[1,2].为了更深层次的利用用户的偏好信息,文献[3]提出了基于深度学习的推荐算法.随着深度学习最近几年的快速发展,许多深度学习算法如xdeepfm,NIFC,NGCF都在推荐系统中获得了较好的效果[4-6].

与xdeepfm,NIFC,NGCF等深度学习推荐算法不同,序列推荐的目标是根据用户历史行为序列来预测用户的“不久的将来”可能的行为,额外考虑了用户的购买动机.为此人们提出了很多解决办法.文献[7]提出基于卷积序列嵌入的个性化Top-N推荐算法,用卷积序列嵌入推荐模型来解决这一问题.其思想是在时间和潜在空间中嵌入一个最近的项目序列到一个“图像”中,并使用卷积滤波器学习序列模式作为图像的局部特征.该方法提供了一个统一且灵活的网络结构,可以捕获一般偏好和序列信息,在公共数据集上得到了较好的效果.文献[8]将基于相似性度量的方法与马尔可夫链结合,对稀疏和长尾数据集进行个性化的序列预测.该方法能够在各种大型、真实世界的数据集上获得较为优秀的结果.文献[9]基于用户的内在偏好和序列模型,提出了一种基于评论驱动的神经序列推荐模型(RNS),文献从评论中提取用户和项目交互,对每个用户或项目进行编码.在用户序列信息的基础上,设计了一种层次化注意力转移机制,以捕捉用户在整体和个人两个层次上的序列信息.该方法在真实的数据集上得到了较好的效果.CosRec提出了一种利用二维卷积网络进行序列推荐的方法,它将项目序列编码为三维张量;使用二维卷积滤波器学习局部特征;并以前馈方式聚合高阶交互特征[10].该方法利用序列特征在公共数据集上取得了较好的效果.传统的序列推荐算法中,大多模型都是对有序项进行处理,因此会受到用户行为序列的单向链式结构的约束,如图1所示,比如用户连续购买电脑主机、键盘和鼠标可能会导致用户有强烈的购买显示器意向,而当图中有植物时就会影响整个推荐的效果.另外使用卷积神经网络CNNs处理序列信息的时候,卷积运算可能丢失部分信息,导致推荐效果有所降低.

图1 用户购买示意图

综上,传统序列推荐模型易受到用户行为序列的单向链式结构约束,如果不适当放宽序列的单向链式结构的约束,将导致用户的突发性购买行为会影响算法整体的推荐效果,且使用卷积神经网络处理序列信息会导致部分信息损失的问题,为了解决此类问题.本文提出了一个深层2D反卷积神经网络的序列推荐算法(Deep 2D deconvolution neural networks for Sequence recommendation algorithm,DdosRec),该算法首先通过成对编码实现不相邻项之间的交互,跳过某些不合理的项目,放松单层马尔可夫序列的约束;其次将传统的CNN处理序列信息的过程中运用反卷积运算,扩充输入数据的信息量;改进反卷积层中的激活函数,使用leaky ReLU替换传统的ReLU,Leaky ReLU的激活功能允许对正信号和很小的负梯度数值,由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习,解决了ReLU函数进入负区间后导致神经元不学习的问题;最后改进神经网络中的损失函数,改进的损失函数可以小幅调节神经网络的损失值,通过人为的调节参数α和β的大小,使神经网络更容易找到损失函数的最小值.可以有效的提高推荐系统的性能.本文对该算法进行了相关的理论推导,并在两个不同的数据集上证明了该算法在平均准确率,召回率等方面表现优异.

2 相关工作

2.1 序列推荐

序列推荐算法通常需要知道用户之前的历史消费习惯,以便用来预测用户未来的消费倾向.为此,近年来出现了很多方法,包括马尔可夫链(MCs),循环神经网络(RNNs),卷积神经网络,基于自我注意力机制的卷积神经网络等[10-13].文献[14]提出了基于时间间隔和自我注意力机制的序列推荐算法,在序列推荐算法的框架内对交互的时间戳进行显式建模,以探索不同的时间间隔对下一项预测的影响.CosRec提出了一个基于二维卷积网络的序列推荐算法[10],将项目编码为三维张量,使用2D卷积滤波器学习局部特征并以前馈方式汇总高阶交互,有效的提高了推荐算法的性能.受此启发,本文先将项目进行成对编码,再用反卷积神经神经网络代替卷积神经网络提取高阶序列信息,将其视为用户的短期偏好.再将高阶序列信息与用户项目交互信息进行融合,形成用户的长短期偏好信息用于推荐.

2.2 卷积神经网络

卷积神经网络(CNNs)的基本结构由输入层、卷积层(convolutional layer)、池化层(pooling layer,也称为取样层)、全连接层及输出层构成.卷积层和池化层一般会取若干个,采用卷积层和池化层交替设置,即一个卷积层连接一个池化层,池化层后再连接一个卷积层,依此类推就形成了一个卷积神经网络.卷积神经网络中的卷积层中输出特征面的每个神经元与其输入进行局部连接,并通过对应的连接权值与局部输入进行加权求和再加上偏置值,得到该神经元输入值,该过程等同于卷积过程[15].

卷积神经网络也被用于其他推荐任务.例如ConvNCF在用户和项目嵌入的外积上应用CNN来估计用户与项目的交互[16].GRec通过一种填隙机制来训练编码器和解码器并使用CNN来实例化通用的GRec算法[17].MARank通过结合剩余网络和多阶注意力机制,在推荐模型中从多个角度统一个人和整体的项目交互[18].SHAN通过两层注意力机制对用户的前几项和长期历史进行建模,以获得用户的短期和长期偏好[19].文献[20]使用CNN设计了一个基于神经网络的传输组件,通过组件改善模型的数据传输效果,以提高推荐效率和推荐准确性.

3 深层2D反卷积神经网络的序列推荐算法

图2 dosrec模块示意图

图2为dosrec模块示意图,该模块由输入端,嵌入查找层,成对编码模块以及2D反卷积神经网络,融合层组成.用户信息|U|和项目信息|I|输入嵌入查找层生成两个嵌入矩阵Eu∈|I|×d和EI∈|u|×d,其中项目嵌入矩阵EI∈|u|×d经过成对编码之后形成三维嵌入矩阵,目的是放宽序列单链的约束,跳过某些不合理的项目.随后将三维嵌入矩阵输入2D反卷积神经网络提取反卷积序列嵌入V(u,t),最后将反卷积序列嵌入V(u,t)和用户嵌入矩阵Eu进行融合.

图3为深层2D反卷积神经网络的序列推荐算法的整体框架,分别由输入端,3个dosrec模块,3个丢弃层,及激活函数ReLU组成.用户和项目的信息经过dosrec模块处理得到反卷积序列嵌入向量之后,第1个dosrec模块的输出不变,第2、3个dosrec模块分别输入一个和两个丢弃层,目的是既充分利用了用户和项目的信息,又在丢弃层的作用下保证训练过程中不会产生过拟合.将其相加并输入ReLU激活函数,随后再计算出用户u可能点击的项目概率,最后利用训练好的神经网络根据用户的嵌入矩阵Eu对t时刻的用户u进行Top-N推荐.

图3 深层2D反卷积神经网络的序列推荐算法示意图

3.1 嵌入查找层

本文所提出的DdosRec算法将通过前L个项目的嵌入矩阵反馈到神经网络中,以捕捉潜在空间序列的特征.将项目和用户嵌入两个矩阵EI∈|I|×d和Eu∈|u|×d,其中d是潜在维数,ei和eu分别表示EI和Eu的第i行和第u行.生成嵌入矩阵以应对用户和项目矩阵中稀疏的id特征,通过将单个id映射成一个稠密向量,变id特征的“精确匹配”为嵌入向量的“模糊查找”,增加高维、稀疏特征数据的可用性,从而提升算法的扩展能力.嵌入查找层通过矩阵相乘实现,可以看成一个特殊的“全连接层”.对于在t时刻的用户u,通过在项目嵌入矩阵EI中查找先前的L个项目来检索输入嵌入矩阵L×d,如公式(1)所示：

(1)

3.2 成对编码

(2)

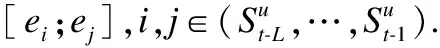
3.3 2D反卷积层

Houtput=(Hinput-1)×s-2×p+k+op

(3)

其中Houtput表示经过反卷积运算后的输出结果,Hinput表示反卷积层的输入数据,s表示反卷积运算中卷积核每次移动的步长,p表示输入的每一条边补充0的层数,k表示卷积核的尺寸大小,op表示输出的每一条边补充0的层数.

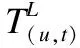
(4)

其中⊙代表反卷积运算符号.

(5)

(6)

(7)

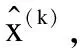
(8)

Bbn1_1=BatchNorm(Ccon1_1)

(9)

使用批量归一化可以使用初始较大的学习率,提高训练的收敛速度,且批量归一化自带正则化的特性,提高网络的泛化能力.一定程度上减少了梯度爆炸的出现,并减少对初始参数的依赖.

将归一化后的结果输入激活函数Leaky ReLU,得到卷积核为1×1的反卷积层处理后的张量C1_1,如公式(10),公式(11)所示[21]：

(10)

C1_1=LeakyReLU(Bbn1_1)

(11)

与CNN网络中常用到的ReLU相比,Leaky ReLU的激活功能允许对正信号和很小的负梯度数值,由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习,解决了ReLU函数进入负区间后,导致神经元不学习的问题.

随后将第1个反卷积层处理后的张量C1_1,输入到第2层中.后续每个卷积层设计除了卷积核大小不同,归一化及激活函数设计均相同.

表1是一个说明性表格.网络中每一部分均由两个卷积层组成:第1层使用1×1的卷积核来丰富特征表示;在第2层中将卷积核大小设置为3×3,随着网络的不断深入,反卷积网络将会提取到更加复杂的序列特征张量C,经过反卷积运算之后扩大了神经网络处理的信息量,有效防止了原卷积神经网络中的卷积运算中的信息丢失问题.最后将反卷积网络的输出张量C输入丢弃层得到张量Cdropout,防止过拟合,提高神经网络处理序列信息的准确性.

表1 2D反卷积网络结构示意图

其中D表示输入项目的嵌入层维度.D1,D2,Ddropout分别表示各层的潜在维度尺寸.FC表示全连接层.

3.4 全连接层

在经过4层反卷积之后将结果输入全连接层,获得更多高阶和抽象的特征,如公式(12)所示:

V1(u,t)=φfc(W[Cdropout]+b)

(12)

其中W∈L×L×2d是将全连接层投影到d维隐藏层的权重矩阵,b∈d是对应的偏置项,φfc是全连接层对应的激活函数,本文采用的激活函数为tanh.V1(u,t)∈d是反卷积序列嵌入,它对前L个项目的各种序列特征进行编码.

为了捕获用户的一般偏好,本文将用户的嵌入矩阵Eu转换为d维向量并与V1(u,t)进行连接,形成第1层融合后的用户和项目序列信息向量Qu1.神经网络第2层在第1层的基础上将Qu1输入到丢弃层形成第2层向量Qu2,将结果输入丢弃层是为了防止层数增加而产生的过拟合现象.如公式(13)所示:

Qu2=dropout(Qu1)

(13)

神经网络的第3层是在第2层的基础上再将Qu2输入到一个丢弃层形成向量Qu3.如公式(14)所示：

Qu3=dropout(Qu2)

(14)

随后将3层神经网络的结果相加之后得到融合向量Qu,如公式(15)所示：

Qu=Qu1+Qu2+Qu3

(15)

将Qu投影到一个带有|Ι|节点的输出层,如公式(16)所示：

y(u,t)=W′[Qu]+b′

(16)

其中,b′∈|Ι|为输出层的偏置项,W′∈|Ι|×2d为输出层的权重矩阵.输出层的值y(u,t)大小与项目i和用户u在时间t上的交互可能性有关.V(u,t)旨在捕获短期序列模型,而用户嵌入矩阵Eu表示用户的长期偏好.Qu则表示经过信息融合后的用户长短期偏好.

3.5 模型训练和推荐

为了训练网络,将输出层的值y(u,t)转换为条件概率,根据用户前L个交互项预测用户的下一个交互项的概率.如公式(17),公式(18)所示：

(17)

其中σ(x)=1/(1+e-x)是sigmoid函数.令Cu={L+1,L+2,…,|Su|}是本文希望为用户u做出预测的时间步长集合.数据中所有序列的可能性如公式(18)所示:

(18)

(19)

本文对二值交叉熵损失函数做了改进,分别在正反馈部分和负反馈部分之前加入一组系数(α,β),其中α+β=1,改进后的二值交叉熵损失函数为:

(20)

改进后的损失函数可以小幅调节神经网络的损失值,通过人为的调节α和β的大小,使网络更容易找到损失函数的最小值.可以有效的提高推荐系统的性能.

模型参数,如Θ={Fk,W,W′,b,b′}等需要通过最小化训练集上的损失值来学习.(d,L,T)等超参数则需要通过在验证集上的测试结果去调节.本文的神经网络通过Adam优化器实现更快速收敛,Adam优化器是具有自适应距离估计的梯度下降算法的一个变体[22].Adam结合了AdaGrad和RMSProp算法的优点,适用于解决高噪声或稀疏梯度的问题,也可以用来解决大规模数据的参数优化问题.

神经网络训练好之后,为了给t时刻的用户u做推荐.本文将用户u的嵌入矩阵Eu提取出来,根据公式(2)给出的最后L个项目的嵌入作为神经网络输入.从输出层y中选取值最高的前N个项目推荐给用户u.

3.6 本文算法步骤

本文的算法步骤见表2.本文的神经网络分3层,第1层用户信息和项目信息分别输入嵌入查找层,项目信息经过成对编码之后,进入2D反卷积神经网络处理得到序列信息,为了捕捉用户的全局偏好,将单层序列向量V(u,t)与用户嵌入矩阵Eu进行连接,形成融合后的用户和项目序列信息向量Qu1.

表2 深层2D反卷积神经网络的序列推荐算法步骤

4 实 验

4.1 数据集和实验环境介绍

本文实验均在CPU为I7-9750H,2.60GHz,内存为16.00GB,显卡为英伟达公司出品的GTX1660Ti的计算机上运行,实验环境为python3.6.参照CosRec的实验评估设置[10],本文在两个标准数据集MovieLens和Gowalla上评估了本文提出的方法.数据集的统计信息如表3所示.

表3 数据集的统计信息

MovieLens:广泛用于评估协同过滤算法的基准数据集.本文在实验中使用了MovieLens-1M版本.

Gowalla:一个基于位置的社交网站,用户通过签到打上时间戳来分享他们的位置.

本文遵循与CosRec中相同的预处理过程:本文将评论或评级的存在视为隐式反馈(即用户与项目交互),使用时间戳来确定操作的顺序,并分别舍弃ML-1M和Gowalla中少于5个和15个操作的用户和项目.本文保留每个用户的行为序列中前80%用于训练和验证,其余20%作为评估模型性能的测试集.

4.2 评价指标

本实验用了平均准确率(MAP),精确率@N(Precision@N)和召回率@N(Recall@N),作为评价指标,其中N分别设置为1,5,10.

平均准确率计算如公式(21)、公式(22)所示:

(21)

(22)

准确率计算如公式(23)所示:

(23)

召回率计算如公式(24)所示:

(24)

其中,N表示给用户推荐的项目个数,M为总用户数量,Iu为推荐给用户的项目集合,Vu是用户u购买项目集合,pui表示i物品在推荐列表中的位置,puj>pui表示j物品在推荐列表中排在i物品之前.

4.3 实验参数设置

本文使用2个反卷积模块,每个反卷积模块由2层组成.维度数从{10,20,30,50,100}中选则,ML-1M和Gowalla分别取20维和100维.在ML-1M数据集中马尔可夫阶数L=6,预测下一个项目的数量为T=3,α设为0.4875,β设为0.5125.在Gowalla数据集中马尔可夫阶数L为1,预测下一个项目的数量为T=1,α设为0.7,β设为0.3.学习率为0.00025,每一组规模为512,负采样个数为3,丢弃率为0.5.上述实验都是使用PyTorch实现的.

4.4 性能比较

本文算法的目的是针对运用序列信息进行推荐展开研究的,可在仅有用户和项目交互信息和时间信息并且数据量较小的情况下生成推荐.故选择需求数据种类相似的算法作为对比方法可以更好的证明算法的性能.本文选择了下列的方法进行比较:

基于流行度的推荐:一种简单的推荐方法,可以根据项目的受欢迎程度对其进行排名.

贝叶斯个性化推荐(BPR):一种经典的非序列个性化推荐方法[23].

基于马尔可夫链的因式分解(FMC):一阶马尔可夫链方法,仅根据最后访问的项目生成推荐[24].

基于马尔可夫链的个性化因式分解(FPMC):FMC和MF的组合,可以捕获短期项目的交互以及用户的全局偏好[25].

GRU4Rec:一种基于RNN的推荐模型,该模型使用RNN捕获序列信息并进行预测[25].

卷积序列嵌入(Caser):一种基于CNN的方法,该方法通过在前L个项目的嵌入矩阵上应用卷积运算来捕获高阶序列信息[7].

CosRec:一种基于2DCNN的序列模型,将项目编码为三维张量,使用2D卷积滤波器学习局部特征并以前馈方式汇总高阶交互[10].

DdosRec-base:为了评估2D反卷积模块的有效性,在其他改动不变的情况下本文创建了ddosrec-base,该版本使用2D CNN而不是使用2D反卷积模块处理序列信息.

DdosRec:本文提出的模型深层2D反卷积神经网络.

从表4、表5的实验结果可知,BPR等未采用序列模型算法的推荐效果比采用序列模型的算法如(caser,CosRec)更差.这个实验结果证实了考虑序列信息的重要性.对比FMC和FPMC,他们只考虑了一阶马尔可夫链进行建模,而CosRec和本文的模型DdosRec可以捕获高阶序列信息,实验证明了考虑多阶马尔可夫链的效果比只考虑一阶马尔可夫链的效果更好.对比GRU4Rec,该算法使用循环神经网络处理序列信息,实验证明Caser、CosRec和本文的模型DdosRec使用CNN处理序列信息在所选数据集中可以取得较好的效果.对比CosRec证明了本文的反卷积模块以及运用更深层网络可以在推荐系统中得到更好的效果.

表4 ML-1M数据集中各个算法实验结果对比

表5 Gowalla数据集中各个算法实验结果对比

对于DdosRec-base模型,在Gowalla数据集上,虽然k=1时召回率和准确率比本文最终的模型要高,但综合指标MAP和其余各项评价指标均是本文的模型DdosRec表现的更好,而在ML-1M数据集中本文的模型的表现在所有指标上领先于DdosRec-base.

综上所述,在Gowalla这种稀疏型数据集上反卷积模块在该模型中召回率、准确率的k值为复数时会有更好的效果,并且对于密集型数据集ML-1M,本文的反卷积模块可以更有效的利用数据集中的多维信息,提高推荐的效果.

4.5 激活函数比较

本节讨论二维反卷积模块中激活函数的影响,其中其他超参数及设置不变,分别创建DdosRec-leaky ReLU和DdosRec-ReLU模型,进行对比实验.

实验结果如表6、表7所示.经过实验对比在ML-1M和Gowalla数据集发现,在大多数情况下比起传统的激活函数ReLU,leaky ReLU在召回率、准确率、和平均准确率3个方面都有较好表现,这主要依赖于leaky ReLU的激活功能允许消息对正信号和小负信号进行编码,由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习,有效的提高了推荐算法的整体效果.

表6 ML-1M中不同激活函数实验对比

表7 Gowalla中不同激活函数实验对比

4.6 网络层数对比

本节通过实验验证本文的模型深层2D反卷积神经网络的层数影响,改变算法模型的层数,当网络结构为:

1层网络时,输入的用户和项目信息通过dosrec模块处理后,直接输入ReLU产生预测;

2层网络时,在dosrec处理过的信息输入ReLU时,会在之前输入Dropout层,并于第一层网络进行相加,利用处理后的信息再产生预测;

3层网络,4层网络设计同理.同时其他参数不变,分别设置DdosRec-1和DdosRec-2,DdosRec-3,DdosRec-4.

从表8、表9中可以看出,DdosRec-1和DdosRec-2神经网络层数较浅,对用户信息和项目的序列信息处理不够完善,会损失一部分信息量,导致推荐性能下降.DdosRec-4中加入丢弃层在一定程度上缓解了过拟合,但是不能完全消除过拟合的影响,并可能因此引入了很多噪音,干扰了推荐的效果,导致实验结果不理想.故本文选取DdosRec-3作为最后的算法框架.

表8 ML-1M中不同层数的实验结果对比

表9 Gowalla中不同层数的实验结果对比

4.7 马尔可夫阶数L和目标数T的影响

本文通过改变马尔可夫阶数L和目标数T探讨本文算法提取高阶信息的能力,与此同时保持其他最佳的超参数和模型设置.分别创建DdosRec-T1,DdosRec-T2,DdosRec-T3,以此来研究马尔可夫阶数L和目标数T变化的影响.

关于马尔可夫阶数L和预测目标数T的影响实验结果如图4,图5所示,在密集的数据集MovieLens中,DdosRec较好的利用了较大L所提供的额外信息,其中 DdosRec-T3的表现最佳,这表明了增大L对推荐效果是有帮助的.对于稀疏数据集,并不是L的值越大越好.因为对于稀疏数据集Gowalla,较高阶的马尔可夫链倾向于同时引入额外的信息和更多的噪声,故DdosRec-T1取得了最好的推荐效果.与DdosRec-T1和DdosRec-T3相比,DdosRec-T2在这两个数据集上的表现更加稳定.

图4 ML-1M数据集中马尔可夫阶数L和预测目标数T的影响

图5 Gowalla数据集中马尔可夫阶数L和预测目标数T的影响

上述实验表明,本文算法在ML-1M和Gowalla数据集上相较其他算法可以取得更好的效果.并通过实验说明了本文算法的激活函数,网络层数以及马尔可夫阶数对推荐效果的影响,证明本文算法网络结构的正确性.

5 结束语

本文主要针对传统方法,利用马尔可夫进行序列推荐时,易受到用户行为序列单向链式结构的约束,如果出现突发性购买项目则影响整体的推荐效果的问题,提出了一种深层2D反卷积神经网络的序列推荐算法.本文在处理信息时对项目的嵌入矩阵进行了成对编码并经过2D反卷积神经网络捕获序列信息,随后和用户的嵌入矩阵进行融合,获得用户的长短期偏好,提高推荐准确性.本文还通过增加dosrec模块的层数并使用Dropout层,既可以充分利用用户和项目的信息,又可以防止过拟合,提高了推荐系统对数据的利用能力.在训练过程中对损失函数进行了改进,使神经网络更容易找到损失值的最小值.通过在Moivelens-1M和Gowalla数据集上的实验证明了,本文提出的算法比起传统的序列推荐算法有效的提高了对序列信息的处理能力,提高了推荐的准确性.