CNCP：一种新型仿生的轻量级电能质量扰动信号分类模型

简献忠，赖左略

(上海理工大学 光电信息与计算机工程学院，上海 200090)

1 引 言

随着越来越多的电子设备在日常生活中的广泛应用，公共电网中产生了大量的电能质量扰动信号[1]，包括暂升、中断、闪烁和尖峰等.这些大量的信号不仅影响到工业生产和生活中正常用电，甚至对电网的安全运行产生了威胁.因此，为了提高电能质量，对电能质量扰动信号进行准确识别至关重要[2].

电能质量扰动信号分类方法分为特征提取和分类决策两部分.针对特征提取的问题，深度学习中常使用的卷积操作已被证明具有优越性[3]，并且在图像分割[4]，图像分类[5]，信号分类[6]中被广泛使用，有效的避免了维数灾难并且提高了分类的准确度.文献[7]提出了一种利用维格纳-维尔分布将一维信号转换为二维图像再通过卷积神经网络(CNN)实现信号分类的模型.文献[8]，与文献[7]相似，提出了一种利用相空间重构将一维信号转换为二维图像再通过CNN实现信号分类的模型.文献[7，8]将一维信号转换为二维图像的过程中人为添加了冗余信息，给CNN提取信号特征增加了难度同时增添了不必要的网络参数.针对分类决策问题，循环神经网络(RNN)可以挖掘信号中的时序信息作为分类策略实现信号分类[9，10]，但是在长序列训练的过程中容易出现梯度消失和梯度爆炸的问题.长短期记忆神经网络(LSTM)通过引入细胞状态并且更新细胞隐藏层的输出[11，12]，有效的解决了RNN在训练过程中可能出现的问题并且具有更强的泛化能力但也使得网络模型更加复杂，参数更多.总的来说，文献[7-12]对以往方法都有改进，提高了电能质量扰动信号分类的准确率，但为了提取到更加深层次的信号特征以及设计更合理的分类策略，整个电能质量扰动信号分类网络模型变得越来越复杂，所需要的参数越来越多.因此，在网络模型设计上还有提高的空间.

为了减少神经网络模型的冗余参数并且有效的提取样本中的时序特征，Mathias Lechner和Thomas A.Henziger等人受到线虫等小型生物大脑神经网络结构的启发，设计了一种轻量级神经回路决策(NCP)[13]神经网络模型.目前，NCP已经在自动驾驶领域对二维图像的实时处理能力取得了不错的结果[13].但是，在一维信号分类上没有相应的研究.为了减少电能质量扰动信号分类模型的复杂性，本文提出了一种基于NCP的信号分类模型(CNCP)，实现了NCP在电能质量扰动信号分类问题上的首次探索.该模型由特征提取，预分类和分类优化3个模块构成.特征提取模块引入一维卷积代替二维卷积来更有效的提取信号的时序特征.预分类模块中优化了NCP中各层的神经元数量，优化后的NCP网络具有参数少，分类决策能力更强等优势，减少了在特征处理过程中信息的损失，更加直观的反应分类结果.分类优化模块，由全连接层组成，防止训练过拟合，提高模型的泛化能力.通过使用IEEE-1159电能质量扰动信号数据集进行验证，CNCP的准确率为98.6%，模型参数为14188个，表明本文提出的模型具有较高的分类准确性及轻量化，更适合在嵌入式设备上实现部署.

2 NCP算法原理

NCP的网络结构如图1所示，图中的神经元之间的粗线表示处于激活状态的突触，细线表示处于抑制状态的突触.感知层的作用是接受信息，对输入进行预处理，实现数据标准化，加快网络的收敛速度.连接层位于决策层和感知层之间，它的作用是对输入信息进行过滤，提取有效特征，避免无效特征对结果进行干扰，同时减少模型参数.决策层被设计成一种特殊的RNN网络模型，特别的是，这一层中各个神经元之间具有突触连接.它的作用是将表层特征提取成有利于最终决策的深层特征.执行层将深层特征进行整合，转化为最终任务的结果.同时神经元之间的连接突触采用激活机制，处于抑制状态的突触将会失效，不会传递任何数据.为了构建NCP网络结构，总结出4项基本原则：

图1 NCP网络架构

1)NCP的网络结构可以分为感知层，连接层，决策层和执行层.

2)前一层的神经元与后一层的神经元之间以二项分布Bin～(n，p1)的方式随机连接，形成突触.突触的极性随机分为兴奋和抑制，其分布满足伯努利分布Ber～(p2).

4)决策层的每一个神经元，以二项分布Bin～(n，p4)的方式随机连接，形成的突触极性满足伯努利分布Ber～(p2).

p1，p2，p3，p4是对应分布的概率，n是后一层神经元的数量.

3 CNCP模型

CNCP整个网络架构分为特征提取，预分类，分类优化3个部分，如图2所示.

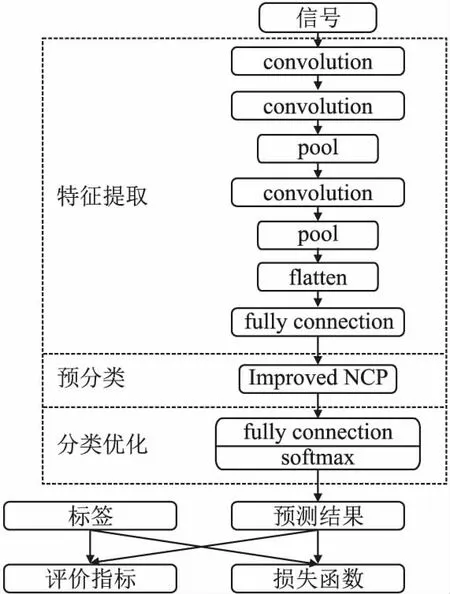
图2 CNCP模型整体架构

1)特征提取，由卷积神经网络构成.其作用是从原始电能质量扰动信号中提取出最具有代表性的局部特征，从而实现特征降维和避免维数灾难.由于电能质量扰动信号是一维的，针对这类具有时序特征的样本数据，常采用一维卷积网络代替二维卷积网络来更好的提取潜在的时序特征，提高分类准确率.并且信号处理以及自然语言处理中得到了广泛的应用[14].在一维卷积网络模型如图3所示.一维卷积与二维卷积的大小一样也可以是二维的，但是只能向一个方向移动，然后对该行或者列计算点乘求和.

2)预分类模块，由改进后的NCP组成.其作用是可以根据改进后的NCP的分类策略对提取到的信号特征实现预分类.改进后的NCP网络如图3所示.图中的神经元之间的粗线表示处于激活状态的突触，细线表示处于抑制状态的突触.感知层，连接层，决策层，执行层分别用圆形，正方形，菱形，三角形.实现表示处于抑制状态的突触，虚线表示处于兴奋状态的突触.为了使改进后的NCP能够针对电能质量扰动信号实现多分类任务，将执行层的神经元优化为信号的总类别数，使得预分类结果能够初步反映各种信号分类可能性，而不是一个简单的标量直接来直接反应样本类别，增加了信息维度有利于提高分类准确率.同时为了防止中间层和决策层特征处理过程中的信息损失，将中间层和决策层的神经元都优化为执行层神经元数量.

图3 改进后的NCP网络架构

3)分类优化模块，由一层全连接层组成，其作用是将预分类结果进行优化，同时提升模型的泛化能力和鲁棒性.优化分类结果通过softmax激活函数输出模型预测到各类别的概率softmax计算方式如公式(1)所示：

(1)

xi表示未经过softmax前得到的该类的预测值，outi表示进过softmax激活函数后的输出概率，softmax的作用就是将网络的预测值转化为该类别预测值的指数与所有类别预测值的指数和的比值，得到每个分类被取到的概率.保证了每一个类别的预测概率处于0-1之间，所有类别的的预测概率和为1. 在多分类问题中，softmax常与交叉熵损失函数搭配，交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在深度学习中就表示为真实概率分布与预测概率分布之间的差异.交叉熵的值越小，模型预测效果就越好.具有求导更快，加速网络收敛的优势.因此选用交叉熵作为模型训练损失函数，计算如公式(2)所示：

(2)

m代表样本数，k代表类别数，p(xij)代表第m个样本的第k类的真实分类标签，q(xij)代表第m个样本的第k类的预测分类结果.通过交叉熵损失函数训练CNCP后，本文输入验证集并通过softmax获得每个类别的概率，将概率的最大值作为最终分类结果.

4 实验结果分析

4.1 数据集

根据IEEE-1159[15]制作暂升(S0)，尖峰(S1)，暂降(S2)，周期缺口(S3)，振荡(S4)，中断(S5)，中断与谐波(S6)，正弦波(S7)，谐波(S8)和闪变(S9)共10类电能质量扰动信号.表1中详细的注明了不同信号的制作方法.然后对信号进行采样，频率为6.4KHz，每个样本总共采集到1280个采样点作为样本特征，结果如图6所示.每一种类型信号取1000个训练集，200个测试集，200个验证集，共14000个样本，同时为了验证CNCP的抗噪性，制作了信噪比由30dB至50dB的电能质量扰动信号，制作好的数据集如表2所示.

表1 电能质量扰动信号的数学模型

表2 数据集

4.2 训练网络以及评价指标

CNCP的网络结构如表3所示，包含了每一层的名称，输出的形状和参数.第1-7层是卷积神经网络，用于特征提取，由一维卷积层和最大池化层组成.第8层是改进后的NCP，用于预分类.第9层是全连接层，用于分类优化.参数共计14188个.

表3 CNCP网络模型

为了评估CNCP在电能质量扰动信号分类问题上的性能，本文根据表2中的数据对网络进行训练，图4显示了网络训练过程中损失和性能的变化.

图4 训练过程图

如图4(a)所示，在训练轮次进行到50次时，CNCP基本达到收敛，训练损失约为0.327.而此时的准确率如图4(b)所示达到了97%，同时训练集与测试集的准确率曲线基本吻合，说明不存在过拟合现象.证明了CNCP具有较强的泛化能力.网络模型训练达到收敛之后，需要对模型进行评价，因此利用训练好的模型对验证集里的2000个样本进行分类，根据分类结果和真实标签计算召回率和准确率，计算公式如式(3)和式(4)所示，TP表示样本真实标签和预测标签都是正例的情况，FP表示真实标签是反例，预测结果是正例的情况，FN表示真实标签是正例，预测结果是反例的情况.

(3)

(4)

4.3 分类正确率比较

为了验证CNCP在电能质量扰动信号分类的可行性，我们以召回率和准确率作为评价指标，将CNCP与其他电能质量扰动信号分类算法进行统一比较.结果如表4所示.小波变换和k最邻相结合的传统分类算法的准确率最低，只有93.1%，低于所有的深度学习分类模型.这是因为深度学习对信号的特征提取以及分类策略都要优于传统方法.CNN的特征提取能力比传统算法更强，因此准确率更高.RNN和LSTM都针对分类策略进行了改进，因此准确率都高于CNN.CNCP进一步优化了RNN网络结构，结果显示其分类准确率要略微高于其他深度学习分类模型.证明了CNCP相较于其他电能质量扰动信号分类方法在分类准确率上优越性.

表4 电能质量扰动信号分类方法的正确率比较(单位：%)

4.4 模型大小及参数对比

为了验证CNCP的模型轻量化程度，我们比较了所用到的网络模型的存储空间，参数，RNN神经元的数量和RNN参数.结果如表5所示.CNN所需的参数数量和模型存储空间较多.这是因为CNN的结构相对简单，为了实现电能质量扰动信号的精确分类，必须要加深网络深度，同时CNN中不存在循环网络结构，因此不统计其RNN核数和RNN参数.CNCP与LSTM都是特殊的RNN网络模型，CNCP模型所需总参数相比RNN减少了大约70%，相比LSTM减少了大约90%.CNCP主要在改进后的NCP网络进行参数优化，因此我们在RNN核数进行比较发现了CNCP相比RNN和LSTM减少了85%.在RNN参数上进行比较发现了CNCP与RNN相比减少了约82%，与LSTM相比减少了95%.由此证明CNCP是一种轻量级电能质量扰动信号分类网络.

表5 不同网络之间模型大小比较

4.5 抗噪性测试

在实际工作中电能质量扰动信号多数是包含噪声的，这将会影响分类方法的准确性，因此对信号分类方法设计了的抗噪性实验.首先根据表2得到信噪比分别为30dB，35dB，40dB，45dB，50dB的电能质量扰动信号各2000个，信噪比为30dB的电能质量扰动信号如图8所示.然后通过不同的分类方法进行分类准确性比较.得到的抗噪性实验比较结果如表6所示.从表中可以看出CNN和RNN受到噪声影响较大，对信噪比为30dB的信号进行分类时准确率都低于90%.小波变换和k最邻相结合的传统分类算法基本不受噪声影响，但是算法本身的分类准确率低.深度学习方法中LSTM和CNCP在信噪比降至30dB时，准确率都能够保持在96%以上，呈现出极强的抗噪性，但是LSTM网络模型所需参数远多于CNCP.由此可见CNCP相较于其他电能质量扰动信号分类方法具有较强的抗噪性.

表6 PQD分类方法的抗噪性比较

4.6 特征分析

波形偏离对称正弦形成的，因此第1个主成分(PC0)反应了信号的整体结构，其余的主成分(PC1-PC9)反应了由于扰动因素而产生的各类电能质量扰动信号在细微处的差异.不同网络模型最高主成分贡献度比较如表7所示.从表中可以看出，通过CNN得到的信号特征的最高主成分重要度最高，CNCP最低.这表明CNN提取到的信号特征更多的表示信号整体结构，而CNCP更多的表示在信号细微处的差异.因此CNCP比CNN，RNN和LSTM在电能质量扰动信号上分类准确率高.

表7 不同网络之间最高主成分贡献度比较

[16]

图5 不同网络之间各个主成分贡献度比较

5 总 结

本文设计了一种基于NCP的轻量级电能质量扰动信号分类模型CNCP，实现了NCP在分类问题上的首次探索.实验结果表明：1)CNCP比wavelet+knn算法分类准确率要高大约5%，比CNN，RNN，LSTM准确率要高大约1%；2)CNCP相比CNN，RNN，LSTM所需要的模型参数和存储空间要少大约65%-90%；3)CNCP在电能质量扰动信号信噪比不低于30dB时，分类准确率能够一直维持了96%以上；4)CNCP提取到的信号特征最高贡献度要低于CNN，RNN，LSTM，表明了CNCP更多的关注在信号细微处的差异，解释了CNCP分类准确性高于其他分类方法的原因.

与其他常用的电能质量扰动信号分类模型相比，本文提出的CNCP模型能够在模型参数较少的情况下具有较高的分类准确度，更加适合在嵌入式设备上部署，为公共电网中电能质量扰动信号的识别问题提供了一种思路.下一步工作将以CNCP为基础，尝试使用ResNet残差网络作为特征提取模块加速模型拟合，从而使用更少的网络层和训练参数，使得模型更加轻量化.