基于BP神经网络的天线场强分布预测方法

王计斌 陈大龙 霍永章

南京华苏科技有限公司

0 引言

无线网络覆盖是决定网络服务的范围，承担着用户与网络之间的无线业务交换的重任，无线网络覆盖的优劣直接影响到用户的服务质量，关系到移动用户的满意度和运营商经济效益。无线网络中的用户分布不断发生变化，原扇区天线方向角是决定覆盖的关键因素之一，为了满足无线网络覆盖的科学优化，如何精准预测天线方向角在调整后场强分布情况是目前研究的重要问题之一。

在场强分布预测的研究常用的射线跟踪模型，需要大量精确的环境数据，应用一般局限于室内，在室外场景中未得到广泛的应用。而人工神经网络(ANN)恰能弥补这个不足，其在场强分布预测中应用的优点是可以在建筑物的形状、参数和结构特征未知的情况下，利用容易获取的一些相关参数得到比较精确的场强值，且能够灵活地适应不同的场景。

目前有文献介绍了某室外微扇区的场强预测方法，它将扇区的地形信息参数输入至神经网络进行训练，并运用实测数据对模型的精度进行验证。有关文献提出一种室外混合预测模型，它将经验模型与 ANN 模型相结合，分别考虑收发端视距 (Line of Sight, LOS )和非视距(Non Line of Sight,NLOS) 情形，此种模型一般用于不同的地形类型，包含城市、郊区等。有关文献介绍了一种室内预测方法，比较了多种类型ANN用于场强预测的效果。有关文献也采用ANN方法，运用机器学习对不同地形进行分类，能够自动提取必要的场景信息进行训练。有关文献介绍了一种混合差分预测模型，其具体做法是利用粗略的场景模型和少量的精确预测值来训练多层感知机神经网络，使得以较小的运算复杂度代价得到精确的场强预测效果。上述各种算法固然能取得较高的精度，然而，是以精确的环境信息的支持为条件的，且某些算法没有真实数据予以验证。

因此，针对上述不足，有必要研究一种基于BP(back propagation)神经网络对天线调整后扇区场强分布的预测方法，利用天线调整前的大量用户数据，通过ANN预测天线方位角调整后天线有效场强分布区域内任意地理位置的接收功率，无需依赖环境数据，与实测数据比较的结果表明，预测误差在合理精度范围内。

1 数据集

方法所使用的数据来源为某市某运营商现网实际数据，数据主要有两种：用户最小化路测（Minimization Drive Test，MDT）数据、扇区工参信息数据。

MDT数据是用户终端设备（User Equipment，UE）在特定时间上报的实时信息数据。最终提供方法所使用的信息有：扇区唯一标识（E-UTRAN Cell Identifier，ECI）、用户经度、用户纬度、海拔高度、时间提前量（Timing Advance，TA）、参考信号接收功率（Reference Signal ReceivedPower，RSRP）。

扇区工参信息数据是一定区域内扇区的基本信息数据，通常一定区域为一个城市或行政区/县。每条数据表示一个ECI相关数据信息，最终提供方法所使用的信息有：扇区唯一标识（ECI）、扇区经度、扇区纬度、扇区方向角、扇区覆盖类型。扇区覆盖类型通常分为：宏站和室分，宏站指的是宏蜂窝扇区的基站，主要是覆盖室外，覆盖面积较大。室分指的是室内分布系统，主要用于改善建筑物内覆盖。

利用BP神经网络算法模型，通过用户实际数据进行训练和算法调优，并进行天线模拟调整后场强分布预测与天线实际调整后场强分布对比，评估算法模型预测的精准度。算法模型的精准度提高需要大量的实际数据进行训练和迭代升级，因此算法模型需要在客户现网训练和迭代一定周期后方可正式投入应用，届时将大大提高传统传播模型的场强分布预测精度，同时为网络覆盖优化节省大量的时间成本和经济成本，并提高网络覆盖优化效率。

2 方法论

提供一种基于BP神经网络对天线调整后扇区场强分布的预测方法，通过ANN预测天线有效场强分布区域内任意地理位置的接收功率，并基于电波传播模型和天线方向图增益变化预测天线方位角调整后的有效场强分布范围内的用户接收功率，无需依赖环境数据；且预测的误差很小。基于BP神经网络的天线场强分布预测方法流程图及具体步骤如图1所示。

图1 基于BP神经网络的天线场强分布预测方法流程图

步骤1：数据收集，收集扇区工参信息数据和用户最小化路测MDT数据；

步骤2：数据整理，对MDT数据和扇区工参信息数据进行整理，剔除异常值，筛选有效数据，并对MDT数据和扇区工参信息数据进行ECI关联匹配；

步骤3：数据栅格化，将扇区分成方形栅格，并将划分的所述方形栅格分为两类，第一类栅格为RSRP数据充足的栅格，用于训练神经网络算法；第二类栅格为RSRP数据不充足的栅格；

步骤4：算法模型训练，采用三层神经网络进行训练，输出RSRP数据不充足的栅格功率；

步骤5：场强分布预测，根据天线方位角调整之后，每个栅格平均接收功率的公式获得天线方位角转动之后每个栅格的平均接收功率，即实现对天线调整后扇区场强分布的预测。

2.1 数据收集

步骤1中，收集最新扇区工参信息数据和近一段时间MDT数据。用户MDT数据包括用户的经度、纬度、时间提前量TA、海拔高度和参考信号接收功率RSRP。工参数据包括扇区ECI、扇区经度、扇区纬度、扇区方向角、扇区覆盖类型。

2.2 数据整理

步骤2中的数据整理，删除异常值的具体方法如下所示：

（1）将MDT数据海拔高度小于0的点，经度和纬度为空或为0的数据，RSRP值不在3GPP所要求的值域区间数据，无ECI数据视为异常数据，予以剔除；再对扇区工参信息数据中经度和纬度为空或为0的数据进行剔除，并且筛选出扇区覆盖类型为宏站的基站扇区。

（2）将海拔数据设为常数0，对上报的用户数据的经纬度进行二维墨卡托投影，且将正北方向对应坐标x轴方向，天线方位角即自天线至测试点的向量与x正轴的逆时针夹角；再将用户点坐标减去天线坐标，得到以天线为原点的用户点的相对坐标，作为新坐标。

（3）将天线场强分布区域划分为多个栅格，所述栅格的大小与全球定位系统（GPS）的精度处于同一数量级；对于每个所述栅格内的不同的用户设备UE所上报的RSRP值，取其均值μ和标准差σ分别设为该位置的用户设备UE的RSRP值作随机变量的均值和标准差，其中：

m为一个栅格内上报RSRP值的用户设备的总数：

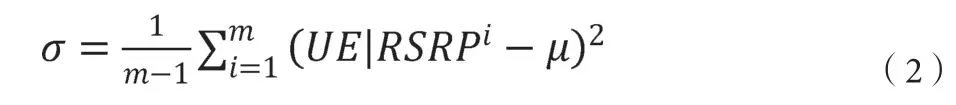
并对栅格内的用户上报的数据求均值μ与标准差σ，取位于[μ-3σ, μ+3σ]范围内的数据，超出该范围的数据则作为异常点并删除。其中由于UE上传的海拔信息往往精度较低，或者没有上传此类数据，故不考虑海拔，均设为常数0；因此对上报的用户数据的经纬度进行二维墨卡托投影，并且将正北方向对应坐标x正轴方向，方位角即自天线至测试点的向量与x正轴的逆时针夹角，例如方位角120度表示UE位置在xoy平面上投影位于从x正轴方向逆时针旋转120度的方向上。

2.3 数据栅格化

步骤3的具体内容为将扇区分成n m×n m的方形栅格，位于某一栅格的用户设备UE的坐标采用该栅格中心的坐标代替，栅格内用户设备UE的RSRP值视为随机变量，基于栅格内所有用户设备UE上报的RSRP数据计算该随机变量的均值和标准差；根据RSRP数据量的不同，将所有栅格分成两类，第一类栅格为RSRP数据充足的栅格，用来训练神经网络；第二类栅格为RSRP数据不充足甚至未上报的栅格，通过BP神经网络预测其对应的栅格功率。

2.4 算法模型训练

步骤4中的具体内容是对RSRP数据充足的栅格采用三层神经网络进行训练，输入层是栅格中心点的坐标(xm, ym)，其中m表示栅格索引号；中间隐含层所包含的神经元个数与训练所采用的样本集规模呈正相关关系，输出层是第二类栅格的RSRP均值的预测值，输入层与隐藏层的常数项神经元是属于偏置单元。

其中隐藏层每个神经元采用的激活函数为：

其中θ_hidden是由输入层到该隐藏层神经元的权重向量，所有隐藏层的神经元的权重向量构成由输入层到隐藏层的权重矩阵；此激活函数对输入特征进行复杂化，以得到更加复杂的特征，从而拟合出从输入到预测输出的更加复杂的拟合函数以提高预测结果的精确性。

输出层采用的激活函数为线性函数：

其中x为隐藏层的输出组成的向量，θoutput是由隐藏层到输出层神经元的权重向量，所有输出层的神经元的权重向量构成由隐藏层到输出层的权重矩阵；该神经网络的层与层之间都有着不同的权重矩阵，权重矩阵的值要进行随机初始化，并随着神经网络的训练不断地优化代价函数而得到最终的最优权重矩阵值，最后得到天线调整前其有效场强分布区内所有栅格RSRP均值的预测值。

2.5 场强分布预测

步骤5中的具体内容是通过场强分布预测模型中的无线电波传播模型，采用无线电波传播公式获得天线方位角调整之后的每个栅格平均RSRP公式，基于无线电波传播公式和天线方向图增益变化预测天线方位角调整后的有效场强分布内的用户RSRP值，即获得天线调整后扇区场强分布的预测。

其中无线电波传播公式为：

该公式中Pt为天线发射功率，G(θ,φ)为天线方向图函数，GT为天线增益，λ为电波波长，d为天线到用户点的自由空间距离，α为路径损耗指数，Pr为接收点的接收功率。

天线方位角调整后的每个栅格平均RSRP公式为：

其中(θ,φ)和(θ^',φ^')分别表示天线姿态调整前后的(方位角，下倾角)，并与天线姿态调整后上报的用户实测数据的均值进行比较，得到的误差作为该算法预测的RSRP均值的误差。其中P_r=P_t•G(θ,φ)•G_T (λ/4πd )^α是在神经网络输出预测值Pt之后，用于计算天线到用户（UE）的路径损耗指数α；并利用计算出来的α计算天线方位角调整后的原用户（UE）的RSRP值；同时只要天线姿态调整幅度不是很大，则对RSRP的标准差基本无影响，基于上述考虑，直接用调整前的标准差作为调整后的标准差的预测值。

2.6 结果检验

对于以上的BP神经网络算法模型，通过激活函数训练得到最终的权重矩阵值，从而得到天线调整前其有效场强分布区内所有栅格RSRP均值的预测值。通过训练出的最优模型，可对预调整扇区新场强分布区域进行栅格化RSRP预测。最终将预算数据与实际调整后用户MDT数据进行对比，判断算法的精准度。

3 实验及结果

3.1 实验

实验收集了某市某运营商7天150个扇区的MDT数据360万用户点，并收集这150个扇区调整后相同周期7天MDT数据379万用户点，评估算法模型的精准度和稳定性。

为保证数据的完整性及有效性，需要对数据进行整理，将MDT数据海拔高度小于0的点，经度和纬度为空或为0的数据，RSRP值不在3GPP所要求的值域区间数据，无ECI数据视为异常数据，予以剔除；再对扇区工参信息数据中经度和纬度为空或为0的数据进行剔除，剔除后有效扇区工参信息149个扇区；并且筛选出扇区覆盖类型为宏站的基站扇区，筛选后宏站扇区143个。将调整前数据作为训练集数据，使用Anaconda软件对模型进行训练，并输出预调整预测数据。将实际调整后用户MDT数据作为验证集数据，对预测数据与验证集数据进行比较，得到RSRP的均值误差，即算法精度衡量。

以下实验结果中选取某市某运营商两个场景扇区的实际数据进行论证，一个是某运营商扇区1，其用户点比较少，分布比较分散，场景简单；另一个是某运营商扇区2，其用户点较多，分布主要集中在街道、居民区，场景复杂。这里未考虑海拔，仅考虑水平面坐标，并且仅针对天线方位角调整幅度不是很大的情况，基于多径衰落的原理，此时可认为路径损耗指数α的变化量可以忽略。

3.2 实验结果

实验过程中发现，BP神经网络算法模型RSRP预测的大部分区域均值误差较小，并得到如下一些过程结果示例。

图2是某市某运营商某区域150个扇区，进行预测数据与验证数据对比分析，分别统计RSRP均值误差小于等于5dB、10dB、15dB的扇区个数占比。从图中可以看出均值误差小于等于5dB的扇区占比达84%，均值误差小于等于10dB的扇区占比达93.33%，均值误差小于等于15dB的扇区占比达99.33%。本算法的预测平均误差在5~8dB，99%置信区间的宽度约为15dB。说明BP神经网络算法模型有较好的精准度。

图2 预测数据与验证数据对比分析图

实验例中扇区1的最大发射功率为52dBm，中心载频的信道号为38496，天线增益为14dBi，天线初始方位角为130度时共有8756个用户点，需要预测若将方位角调整为150度其覆盖区域的场强分布，天线方位角为150度时有4803个用户点可供比较计算预测误差。

对扇区1天线调整后的场强分布进行预测，误差绝对值均值达到5.00dB，96%以上的分布区域的预测误差小于15dB。算法预测的UE的RSRP与信号覆盖区域内UE上报的RSRP的差值作为预测误差，大部分区域的预测误差较小。

天线方位角调整至150度域内UE上报的RSRP值和算法得到的域内UE的RSRP预测值的统计直方图分别如图3和图4所示，图中显示，二者统计规律也是基本一致的。

图3 扇区1天线方位角调整至150度，域内UE上报的真实RSRP值的统计直方图

图4 扇区1天线方位角调整至150度，算法得到的域内RSRP预测值的统计直方图

实验例中扇区2的最大发射功率为53dBm(折合成线性功率约200W)，中心载频的信道号为37900，天线增益为14dBi，天线的初始方位角为130度时有34459个用户点，需要预测若将方位角调整为150度其覆盖区域的场强分布，天线方位角为150度时有17849个用户点可供比较计算预测误差。

通过算法模型对该扇区2天线调整后的场强分布进行预测，误差绝对值均值达到7.40dB，90%以上的分布区域的预测误差小于15dB，大部分区域的预测误差较小。

天线方位角调整至150度域内，UE上报的RSRP值和算法得到的域内UE的RSRP预测值的统计直方图，分别如图5和图6所示，图中显示，二者统计规律也是基本一致的。另外，图7为扇区2将天线方位角调整至150度，域内UE上报的RSRP值分布图。图8为扇区2将天线方位角调整至150度，算法得到的域内RSRP预测值分布图。通过对比，两图直观地反映，两者的数值及其分布趋势是基本一致。

图5 扇区2天线方位角调整至150度，域内UE上报的真实RSRP值的统计直方图

图6 扇区2天线方位角调整至150度，算法得到的域内RSRP预测值的统计直方图

图7 扇区2将天线方位解调整至150度，域内UE上报的RSRP值分布图

图8 扇区2将天线方位解调整至150度，算法得到的域内RSRP预测值分布图

通过扇区1和扇区2的实例结果表明，实例的预测平均误差在本算法误差区间5~8dB，99%置信区间的宽度约为15dB。

4 结束语

一种基于BP神经网络对天线调整后扇区场强分布的预测方法，基于BP神经网络算法通过MDT用户测量数据建模，预测天线调整后扇区场强分布，规避了单独使用传播模型的一些缺点，提高了预测的精准度和稳定性。经实际调整测试证明模型的精准度如下：预测平均误差在5~8dB，99%置信区间的宽度约为15dB，并与各实测场景表现一致。通过栅格级用户数据RSRP热力分布，进行调整前和调整后RSRP分布变化对比，对网络覆盖优化工作具有指导意义。

对于BP神经网络的算法设计还存在一定的不足，需持续增加数据样本对算法进行持续学习训练，并且对每一个扇区的模型权值进行存储，从而进一步提升算法精度。