积累基本活动经验的图形与几何教学策略研究*

孙新宇 吴秀君，2，T 郭梦媛 叶舒琪

（1.江汉大学人工智能学院，武汉，430056；2.江汉大学武汉研究院，武汉，430056）

根据国内外关于活动经验的文献和教育理论，不难发现人们都十分赞同“活动促进学习”“从做中学”的观点，重视新经验与旧经验的联结[1-6]。但大部分实践研究都只注重教师的活动教案设计和学生参与方面，真正运用在活动教学过程与实践操作中的研究不够完善，提出的教学建议比较零散，缺少系统性，教师在真正教学实践时难以把握。针对上述情况，我们将基于数学活动经验的视角，进行初中图形与几何的教学策略研究。

2021 年9 月至2021 年12 月，我们在武汉市某初中对学生进行问卷调查和对数学教师进行访谈，了解基于数学活动经验的初中图形与几何教学现状。然后，在该初中进行为期四个月的课堂观察，依据建构主义学习理论、杜威的经验主义理论、弗赖登塔尔的数学教育理论和奥苏泊尔的认知同化学习理论提出相应教学策略，然后在两个教学班进行教学实践与策略修正。初中阶段是学生开始从形象思维向着抽象思维发展、转变的时期，图形与几何的计算、演绎推理复杂度不断跃升，对于大部分学生还是有很大的挑战性的。同时图形与几何这一部分无论计算还是证明，都需要严格的写作规范与依据，是培养学生严谨性和规范性的重要时期。下面结合自身课堂观察，在实践中积累的案例和优质课案例库研读对数学活动经验视角下的初中图形与几何教学策略。

一、设置合适的导入方式，唤醒学生的原始经验

从学生问卷结果可以看出，绝大多数学生在学习图形与几何新内容时会借助以往的知识经验，因此教师在进行新的图形与几何内容教学前，需要了解学生具备哪些原始经验，去设置能够唤醒学生原始经验的情境导入。教师可根据具体内容设置新知引入的类型，大部分教师会选择创设生活情境引入新知和复习旧知引入新知两种类型。

创设生活情境引入新知这种类型，非常适合与日常生活相贴近的数学知识，这样的教学设计能够引起学生的共鸣，从而激发学生继续学习探索的兴趣，培养学生的情感性经验。比如在黄金矩形教学中从观察收集美丽的矩形物品导入。又如，在探索轴对称的性质时，教师可以创设能引起学生动手、观察和思考的生活情境。活动一：观察屏幕中自然景观、建筑物以及日常生活用品的图片，它们有什么共同特点。活动二：把纸对折，在折痕不被完全剪断的情况下剪出一个图案。通过动手操作、观察这样的活动，让学生体验轴对称图形的特点以及在生活中的应用，积累动作性经验和观察性经验。

复习旧知引入新知的类型适合前后知识联结性强的教学内容。比如在探究平行线的性质时，教师通过提问“上节课学习的平行线三种判定方法的条件、结论分别是什么？如果把判定方法的结论和条件反过来，还成立吗？”来引入探究课题，有意识地让学生回顾前面学习的知识，通过类比研究平行线判定的过程去研究平行线的性质，积累学生归纳、类比的抽象性活动经验。如果教学时间不够，导入环节可以提前到课外进行，提前唤醒学生需要的原始经验。

二、设计实践和探究性的数学活动，留给学生充足的参与时间

根据学生问卷显示，虽然只有58%的教师会布置探究性的作业，但大部分学生愿意去完成探究性的作业，因此教师应该在图形与几何的教学中有意识地多设计实践性和探究性的数学活动，并在进度安排上留出足够的时间给学生进行动手操作、观察、思考、探究、归纳和表达，至于课堂探索时间与进度的冲突问题，可以借助线上平台在线上或者课下的前置性活动进行预备，缩短课堂上的探索时间。

实践和探究性的数学活动能有效调动学生的求知欲，激发学生学习积极性，在问题探究中获得推理能力的提升，体会获得知识的愉悦，增强学习数学的信心，有效改善学生推理能力不足的现状，有效促进学生情感性经验、动作性经验、观察性经验和抽象性经验的积累。比如，教师通过设计“平行线分线段成比例”“平行线分线段成比例在相似三角形的应用”“相似三角形的判定”“相似三角形判定的变式应用”的数学活动引导学生在做数学活动中对知识经验一步步深化吸收，最终实现“相似三角形”新知在原有“三角形”与“相似图形”认知结构中的同化，积累数学活动经验。

又如，在探索等腰三角形的性质时，教师设计如下活动：（1）按教材给出的方式剪出等腰三角形；（2）观察剪出的等腰三角形纸片，概括剪出的等腰三角形的特征；（3）观察其他同学剪出的等腰三角形，是否都具有上述概括的特征；（4）在练习本上任意画出一个等腰三角形，剪下来折一折，是否符合前面概括的特征。由此概括出等腰三角形的性质，其中活动一是实践性数学活动，活动二和活动三属于探究性数学活动，活动四是实践与探究相结合的活动。整体活动安排为学生先对一个等腰三角形研究发现其特征，然后在对其他等腰三角形进行研究发现特征的一致性，从而概括出等腰三角形的形式，在折叠、观察、思考和讨论的过程中充分体验特殊到一般的归纳方法，积累学生的思维性经验。

三、采用问题引导的教学方法，培养学生的抽象性经验

抽象性经验主要有猜想、思考、归纳、推理、表达。通过学生问卷和教师访谈显示，学生的表达、归纳和推理等能力不足，教师在课堂中未能在思考探究环节留给学生充足的时间，当学生难以解决问题时，部分教师会直接给出结论从而导致学生的表达、归纳和推理等抽象性经验积累不足，不利于发展学生的问题解决能力。教师在数学教学活动中要做引领者，当学生难以进行数学活动的任务时，要及时设置问题串，打破学生与问题间的隔阂，引导学生在一步步、循序渐进解决问题的过程中，经历知识的再发现、再创造，感受数学魅力，获得探索的乐趣和成就感，培养情感性经验和分析、归纳、推理、反思等抽象性数学经验。比如学生理解不了黄金矩形第三步的折叠方式时，依据再创造理论，教师用展示和提问的方式引导、帮助这部分学生去思考理解，进而实现“黄金矩形”的再创造，也为后续黄金矩形的验证提供了思路，有效积累了学生动作性经验和思考、推理的抽象性经验。

又如，在探索圆周角定理时，教师让学生测量同一圆弧所对的圆心角和圆周角的度数，并回答以下问题：这两个角有怎样的关系？继续在圆上任取一条圆弧，再次测量这条弧所对的圆心角和圆周角的度数，你还能得出同样的结论吗？学生在教师一步步提问和参与活动中发现结论，积累了猜想、分析等抽象性经验。

四、借助数学软件，让学生在观察和操作中发展空间想象和几何直观

图形的变化一直是图形与几何教学中的难点，由于学生缺乏对图形变化轨迹的空间想象，所以仅仅依靠教师的讲解难以理解和解决问题。通过教师访谈，了解到不少数学教师在讲解图形与几何时，会利用几何画板等将图形变化变得直观化的数学软件帮助学生想象、理解，特别是在新授课的探究环节和习题课的讲解环节。

在学生猜想的基础上，教师利用几何画板的直观性和准确性，帮助学生加深对平行线分线段成比例的理解和记忆，发展学生的空间想象和几何直观。习题是考察学生对“图形的变化”掌握情况的有效途径之一，特别是图形与几何中的动点问题，很多学生因为想象不出图形的运动轨迹导致问题未能解决。例如，等腰△ABC中，∠BAC=120°，AB=AC=，点D在边BC上，CD=2，将CD绕点C逆时针旋转α°到CE，连接AE，以AE、AB为边做平行四边形ABFE，连DF，求DF最大值。教师在讲解这个动点问题前，通过询问了解到有超过一半的学生不会做的原因是想象不出来F点的运动轨迹，只要明确了F点的运动轨迹，就可以根据三角形的三边关系找到DF的最大值，所以解题的关键点在于明确F点的运动轨迹。学生大部分能想象和发现E点的运动轨迹是个圆，还有少部分能理解F点的运动是跟随E点变化的，但想象理解不了F点的运动轨迹和E点的运动轨迹在形状、大小上是一样的，所以教师借助几何画板，拖动E点，学生在观察几何画板中E点和F点的轨迹变化过程中，培养他们的空间想象和几何直观，积累思维性经验。

五、引导学生归纳小结，教师课后进行教学反思

根据学生问卷结果显示，有64%的学生很少会在学习活动后进行归纳，甚至从来不会归纳，这也能说明有64%的学生不能很好解决问题的原因，因此教师应该注重对学生归纳能力的培养，进而提高学生的问题解决能力。归纳小结存在于教学活动中的知识点小结和课堂内容小结，小结环节不仅可以帮助学生梳理知识结构，将新的活动经验融入到原有经验结构中，还可以从学生给出的反馈看出本堂课教学目标达成的大致情况，但具体目标完成情况还需要结合习题、作业的完成情况来分析。这些做法有利于教师对自己的教学进行反思，发现教学中存在的问题，从而使得后续的教学更加完善。

例如，在教师讲解角的概念后，以做答题游戏的形式促进学生对角的概念的认识归纳，培养学生的问题解决能力，从答题的速度和准确率检验学生对角的概念教学目标的掌握情况，及时调整教学进度。此外，做游戏的形式能极大提高学生数学学习的兴趣和主动性，有利于推进后面的教学环节。

课堂结束后，教师也应该引导学生对本节课所有的知识点进行归纳小结，将学到的新知识经验及时梳理构建知识框架，促进知识经验的吸收。如在讲解完角的比较与运算后，教师引导学生回顾本节课的主要内容，构建知识与方法的框架（如图1），完善学生的认知结构。

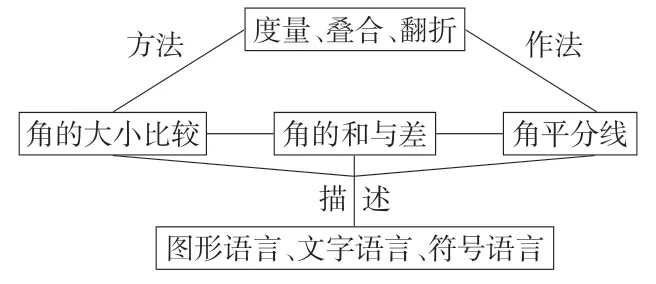
图1 知识框架图

六、利用线上平台和工具，合理安排数学活动流程

教师访谈结果显示，教师在课堂上未能留给学生充足的时间思考探究，因此教师应该合理安排教学流程，利用线上平台增加课外实践应用的环节，使学生能在数学活动中充分体验探索数学的乐趣，积累数学活动经验。

课前教师可以将活动预案通过PPT 或者小视频的方式发布到班级线上平台，如QQ 课堂、雨课堂、教育云等互动交流平台，让学生在课前提前理解活动的要求与内容，留足时间、动员家庭成员一起完成活动预案，为课上的新知探究环节预备好需要的原始经验。如课前“收集好看的矩形”活动任务的布置，不但能够使得学生在完成课前活动任务的过程中唤醒原始经验，还能够在课堂上留给学生更多的时间去思考探究，积累数学活动经验。

课后学生可以以小组形式进行网上讨论并推举小组最佳作品参加网上作品展示与互评，增加作品的反馈环节，加强学生互助合作与情感交流，这样有利于增加集体荣誉感。