解析几何运算细节的优化策略及教学建议*

赵 刚 (江苏省徐州市第一中学 221002)

丁永刚 (江苏师范大学数学与统计学院 221116)

纵观近几年高考解析几何试题可见其主要特点：一是以过特殊点的直线与圆锥曲线相交为基础设计“连环题”，结合曲线的定义及几何性质，利用待定系数法先确定曲线的标准方程，再进一步研究弦长、图形面积、最值、取值范围等；二是以不同曲线(圆、椭圆、双曲线、抛物线)的位置关系为基础设计“连环题”；三是判断曲线和直线位置关系，综合性较强，往往与向量(共线、垂直、数量积)结合，涉及方程组联立、根的判别式、根与系数的关系、弦长问题等，试题运算量较大，需要繁杂的讨论，不但会影响解题的速度，甚至会导致学生“望题兴叹”“望而却步”.学生在求解解析几何问题时，往往能够理解数学对象，但在设计运算程序时往往会有比较大的偏差.这就导致一部分学生在解题时运算量偏大，无法算出正确结果[1].为了提高运算效率，笔者通过实例说明解析几何中运算细节的优化策略，归纳出解决此类问题的一些方法和技巧.

1 运算优化策略

1.1 重视定义，揭示本质

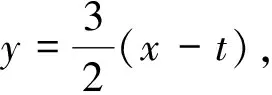
反思 涉及焦点与抛物线上的点时，结合图形运用圆锥曲线的定义，可回避复杂的计算[2].定义是性质的“根基”，牢记圆锥曲线的定义，将定量的计算和定性的分析有机结合，可大大降低运算量.

1.2 抓住零元，优化设线

解析几何中经常会碰到过定点(a,0)的直线问题，对此学生往往会分类处理，将直线设为y=k(x-a)或x=a，笔者建议将直线设为x=my+a.两种设法虽然都很简洁，但运算量却相差很大.

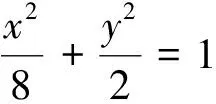
图1

解法1①当直线l斜率存在时，设直线l的方程为y=k(x-2)(常规设法).

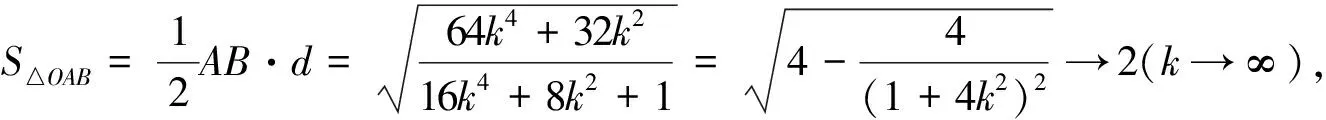
②当直线l斜率不存在时，易得A,B两点 坐标分别为(2,1)，(2,-1)，故AB=2.此时S△OAB=2.

解法2由题意可知直线l的斜率不为0，故可设其方程为x=my+2.

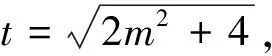
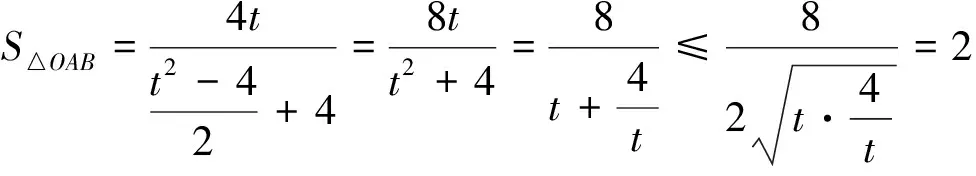
反思 解法2的算法简洁，运算量小.事实上，解法1中将直线l的方程设为y=k(x-2)，与椭圆联立后所得方程(1+4k2)x2-16k2x+16k2-8=0形式复杂，参数k出现频数较多，直接导致了后续运算量增大.而解法2将直线l的方程设为x=my+2，与椭圆联立后所得方程(m2+4)y2+4my-4=0形式简洁，参数m出现频数较少，所以后续运算量也比较小.如果广义理解直线l斜截式方程y=kx+b的本质，抓住其简洁的特征是因为直线l所过的定点(0,b)恰好在y轴上，那么用对偶的思想去分析就会得到，当直线l所过的定点(a,0)在x轴上时，就应该把直线l的方程设为x=my+a.这种设法使方程达到最简，其根本原因是充分利用了“0”元素.

1.3 巧用不等式，化简分式

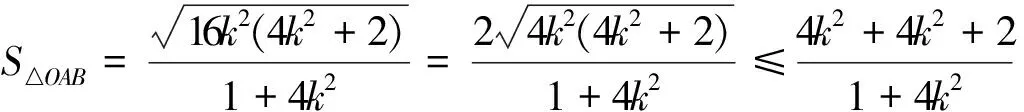
反思 在具体解题中需要关注分式结构特征，通过调配系数，使得分式满足基本不等式的使用条件，从而实现简化运算.

1.4 借助同构，简化计算

当题目中出现图形对等，并且图形满足的条件相似时，就具备了同构法的使用条件.

例3已知抛物线y2=2x上三点A(2,2),B,C，直线AB,AC是圆M:(x-2)2+y2=1的两条切线，求直线BC的方程.

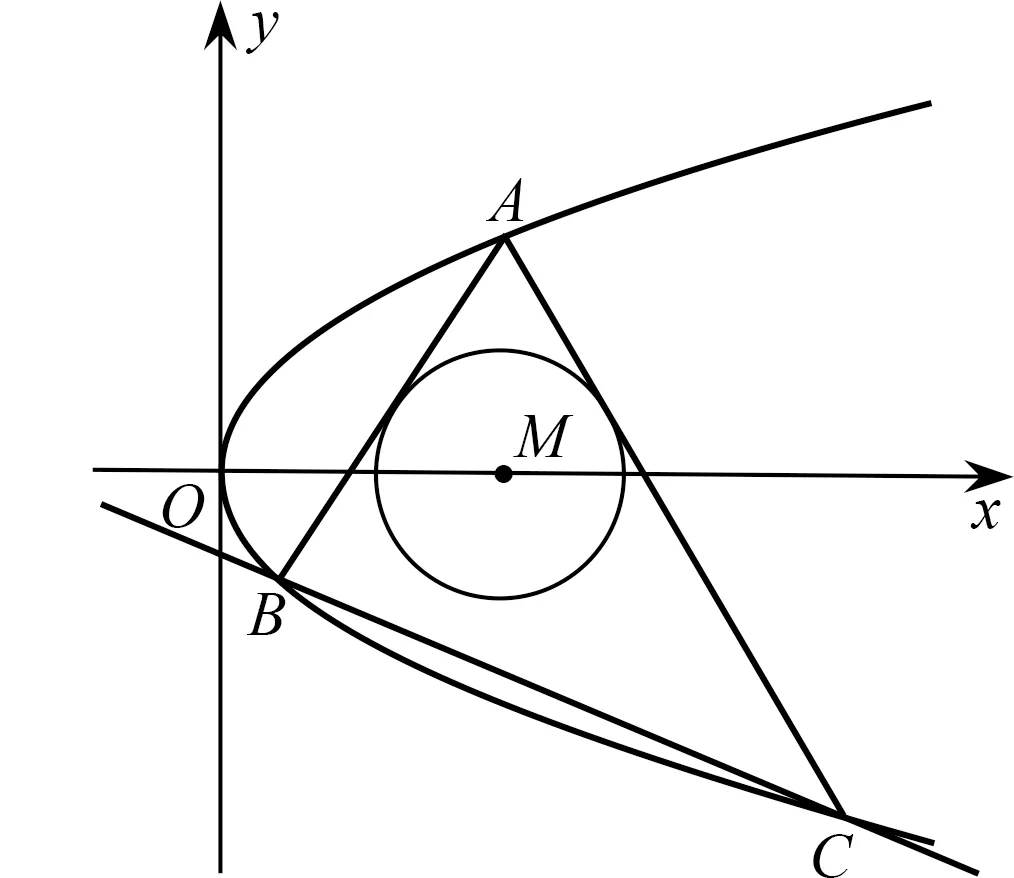
图2

反思 解法1思路清晰，但是计算量很大且易错.如果注意到题目中AB,AC均为圆M的切线，说明AB,AC地位相同，且点B与点C均在抛物线y2=2x上，故只要求出点B的坐标所满足的关系，就可以得到点C的坐标所满足的关系，从而得到直线BC的方程.解法2利用点B与点C结构相同，通过探求点B满足的关系，从而求得点C的关系，巧妙地规避了复杂的运算，这种算法充分说明在运算中要注重探究运算思路，避免单纯机械的计算.

1.5 利用曲线系，巧求切线

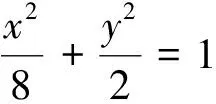
解法1(常规解法)设所求切线方程为y-1=k(x-2),

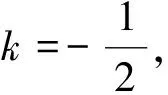
反思 运用这种解法非常简洁，对于求圆及椭圆这种闭合曲线上一点处的切线方程均可以采用此法来简化运算.需要注意的是，借助这种方法求切线方程，必须先把切点表示成特殊的“曲线”形式，即与所给曲线结构相同才可以，否则令λ=-1就得不到切线方程.

1.6 点代平方差，简化问题

图3

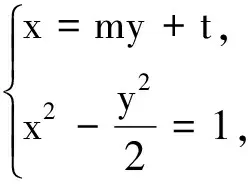
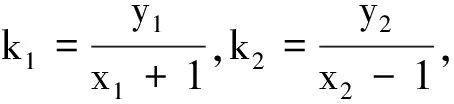
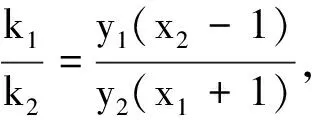
解法2通过数式变形，使得问题可以直接借助韦达定理解决，算法清晰简洁，计算复杂程度降低.

1.7 通过平几，化简转化

解析几何源于平面几何，在解题过程中，运用相关的平面几何性质，常常能达到事半功倍的效果.

在例5的求解过程中，如果注意利用双曲线的几何性质“双曲线上任意一点M与关于原点对称的两点A,B的连线MA,MB斜率之积为定值”,则可以大大简化计算.

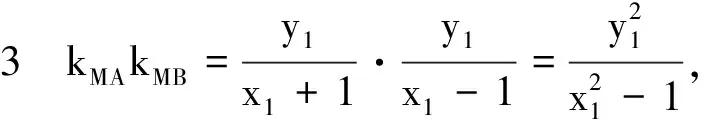
反思 题目中出现多个点和多条线时，设点还是设线，理清“点变”中不变的本质，会减少计算量[2].不同的选择往往直接影响后续的计算量和难度.从例5的探究中可以发现，几何性质的运用可以在一定程度上简化运算.而学生在解题时能否挖掘到一些几何性质，则取决于学生平时的积累.这就要求教师在平时的教学中，要注重对学生探究能力的培养，注意结合几何图形开展探究，鼓励学生大胆设想、推导，引导学生结合圆锥曲线定义及图形对称等角度进行论证，并通过师生互动、生生互动等方式进行研讨，从而整体提升学生的探究能力及教师的教学水平.

2 解析几何教学建议

弗赖登塔尔说过：“老师不该将数学定义、规则、算法灌输给学生，应该让学生体验、发现数学知识.”传统教育理念下的教师在课堂上一个人唱独角戏，独自完成知识传授，而新教育理念下教师改进学生的学习方式，让学生展示自己的思维过程.“举一反三”是接受学习的写照，学习方式的转变关键不在于是“发现的”还是“接受的”，而在于学生数学思维的参与程度.在解析几何的教学中，笔者使用了上述多种运算优化策略，一题多解、一题多变、层层递进，解题思路都是在与学生的互动碰撞中产生的，学生思维的创造性、深刻性得到了真正的训练,真正实现了深度学习.

解析几何教学要从数学基本技能出发，提高学生的数学素养，同时体现显性目标(双基)和隐性目标(数学能力、理性精神).

2.1 教学目标由“知识中心”向“能力中心”转变

教学目标应由“关注知识传输”向“关注能力提升”转变，解析几何教学要关注学生计算的实际水平，安排合理的计算程序，使其计算更高效.课程设计由“传统的知识灌输”转向“教改后引导活动”，让学生在简化计算的活动中获得自信.培养学生勤于动手的良好学习风貌.当前，“满堂灌”已被教师摒弃,但是“满堂问”却比比皆是.满堂问实则为“按教师设计程序”的接受式学习.探究解析几何计算优化策略的过程中笔者给学生提供了足够的机会，让学生依据自己已有的知识和经验主动建构知识体系，真正培养了学生的学科核心素养.

2.2 教学观念由“统一规格”向“差异教育”转变

课程目标应致力于“打好基础，促进发展”.“一刀切、统一规格”是当前教育的一个突出问题，显而易见，“一刀切”教育不利于人才培养.笔者在解析几何习题计算中使用的一题多解都是由学生独立完成，充分尊重了学生的个体差异，让学有余力的学生在课堂上有机会体现自己的价值，真正实现了差异性教育.

2.3 认知活动由“重视结果”向“重视过程”转变

习题只给学生对对答案是当前不少解析几何习题课的教学现状.过程远比结果重要，缺少过程的结果是无源之水、无本之木.数学概念、原理、定理应引导学生通过抽象概括得出结论，过程是不能省略的，解析几何的运算教学中，笔者引导学生重视每一个解题过程并思考如何优化计算，在过程训练中逐渐理清解题思路.

总之，教师在教学中要不断研究教材、研究学生、研究教法、研究习题，在解决复杂的计算时要积极引导学生，通过师生互动、生生互动、生本互动，拓宽解题思路，“从无到有，无中生有”，从各个角度给出解题探索.让学生的解题速度“从慢到快”、解题经验“从少到多”、解题能力“从弱到强”，“让学习更加自然，让备考更加轻松”，让学生的数学品格、数学观念、数学素养同步提升[3].