基于观测器构造不同阶混沌系统的广义同步理论研究*
2022-11-17徐燕燕
徐燕燕
(江西机电职业技术学院,江西 南昌 330013)
0 引言
实现混沌同步的方法有多种,如自适应控制同步[1]、观测器控制同步[2]、滑模控制同步[3]、脉冲同步[4]等。现有文献大多集中在混沌系统完全同步方面,广义同步的研究很少,关于不同阶混沌系统的研究更少。然而,在复杂网络系统中,如脑混沌的研究,可以利用低阶系统驱动高阶系统达到同步;循环系统和呼吸系统可以达到一致的行为。但两系统本身的性质却有着本质的差别,并且是不同阶的,因此,研究此类问题有助于弄清复杂系统间的相互联系[5-10]。
笔者通过对状态观测器进行扩展,设计控制器和参数自适应律,基于预先确定的响应系统的状态变量与驱动系统的状态变量的函数关系,采用解析法构造了混沌广义同步的响应系统。提出的同步方法不要求驱动系统的线性部分稳定就可以实现不同维混沌系统间的线性广义同步,并且通过自适应控制可以降低控制能量,提高同步速度,在实际中有更广泛的应用。
1 问题描述
考虑如下两个动力系统:

其中,式(1)为驱动系统,式(2)为待构造的响应系统;x∈Rn,y∈Rm,F和G可以是不同的函数。对于给定的映射φ:Rn→Rm,如果系统(1)和系统(2)满足||x-φ(y)||=0,则系统实现了广义同步。若m=n,且φ为恒等映射,即为一般意义下的完全同步。
不失一般性,驱动系统(1)可分解为:

其中,Ax是F(x)的线性部分,f(x)是F(x)的非线性部分,A∈Rn×n是系数矩阵。有许多混沌系统可以做上述分解,如Chua’s电路、Lorenz系统、Chen’s系统、Liu系统等等。
设系统(3)的输出为:

其中,C∈Rn为输出矩阵。C的选择可以使系统所有状态变量参与,也可以使部分可观测的状态变量参与。
研究的目标是构造一个系统(2)的具体结构,并在合适的控制器作用下,实现广义同步。
在考虑线性广义同步的情况下,有:

T∈Rn×m,n≤m,即所构造的响应系统可以是不小于驱动系统阶数的任意阶系统。以下将构造出响应系统(2),并使之符合(5)。
首先对混沌系统和混沌信号做出如下假设:
假设1:
||h(x,t)||≤γ(x),∀x,t;||l(y,t)||≤β(y),■y,t,且γ(t)和β(t)是连续的。
一般情况下,不管系统是处于平衡点、周期和混沌情况下,对所有的时间t均有:
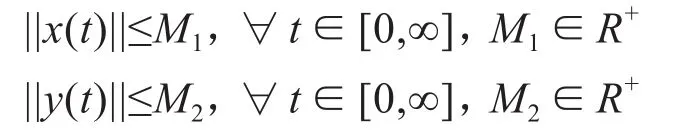
那么,在假设1满足的情况下,存在W,T∈R+,有:

首先引入变量e和ε,用e和ε分别表示状态变量误差向量和输出误差向量,则:

定理1:若系统(2)满足:

T∈Rn×m是所选择的任意矩阵,n≤m,T+∈Rm×n是矩阵T的伪逆矩阵,有TT+=In,In是n阶单位矩阵。g(y)是可选择的非线性函数,可以与f(x)相同,也可以不同,B和D由条件1求解,则在(A,K)满足能观测的条件下,即rank(K;KA;...KAn-1)=n时,系统(3)和(7)构成的驱动—响应系统满足线性广义同步式(5),且系统(7)是系统(3)的广义状态观测器。
条件1:

其中:P、Q、L是适当维数的正定矩阵。
现设计一个具有如下形式的控制器U(t):
U(t)=m0tanh(Kε),其中m0∈R+,L由式(9)确定,称为控制器的学习速率矩阵。
下面给出证明:变量误差e=x-Ty,则误差动态系统为:
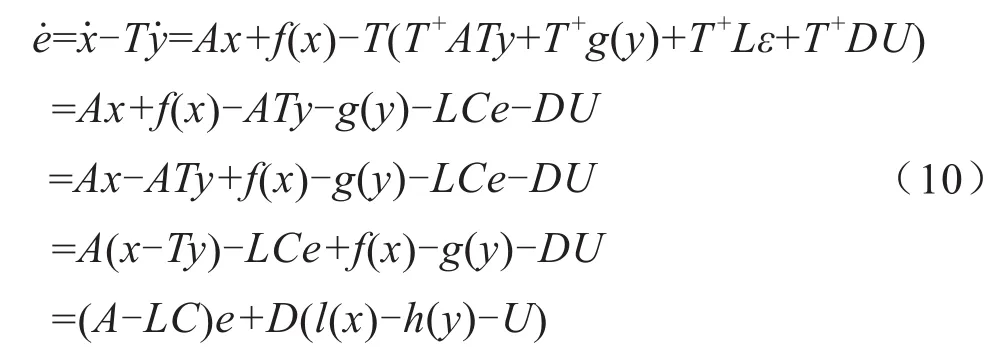
其中,l(x)=(DTD)-1DTf(x),h(y)=(DTD)-1DTg(x)。
选择Lyapunov函数为:V(e)=eTPe≥0
则:

由于sgn[Kε]TKε=||Kε||,所以因此,当系统满足条件1、假设1和式(6)的前提下,有如下结论:选择m0≥2(W+T)时,为一负定函数,则式(10)的平衡点e=0是大范围渐近稳定的,那么系统(3)和(7)实现广义同步。
当选择的m0不满足m0≥2(W+T)时,则不能确定两系统是否实现同步控制。当选择的m0远大于2(W+T)时,虽然能实现同步且有较快的同步速度,但所需的控制能量较大,较大的控制能量在某些场合时不允许的,因此,正确估计出m0的大小并实现同步控制是必要的。可通过对m0设计自适应调节律来实现。给出如下定理。
定理2:考虑的两个系统分别满足条件1、假设1及式(6)的前提下,设计如下形式的自适应控制律:
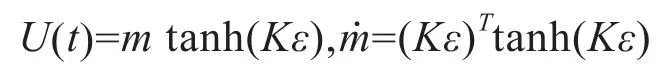
能得出如下结论:
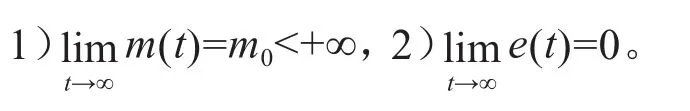
证明:
选择如下形式的Lyapunov函数:
V(e,m)=eTPe+[m-2(W+T)]2
则:

将[Kε]Tsgn(Kε)=||Kε||代入上述不等式可得到)<-eTQe≤-λmin(Q)||e||2,那么:

即定理2得证。
2 仿真实例
为验证上述结论,下面给出蔡氏电路系统的数值模拟结果。其动力学模型如下:

其中,f(x1)=bx1+0.5(a-b)(|x1+1|-|x1-1|),当a=-1.27,b=-0.68,α=10,β=14.87时,系统(11)处于混沌状态,其吸引子相图如图1所示。
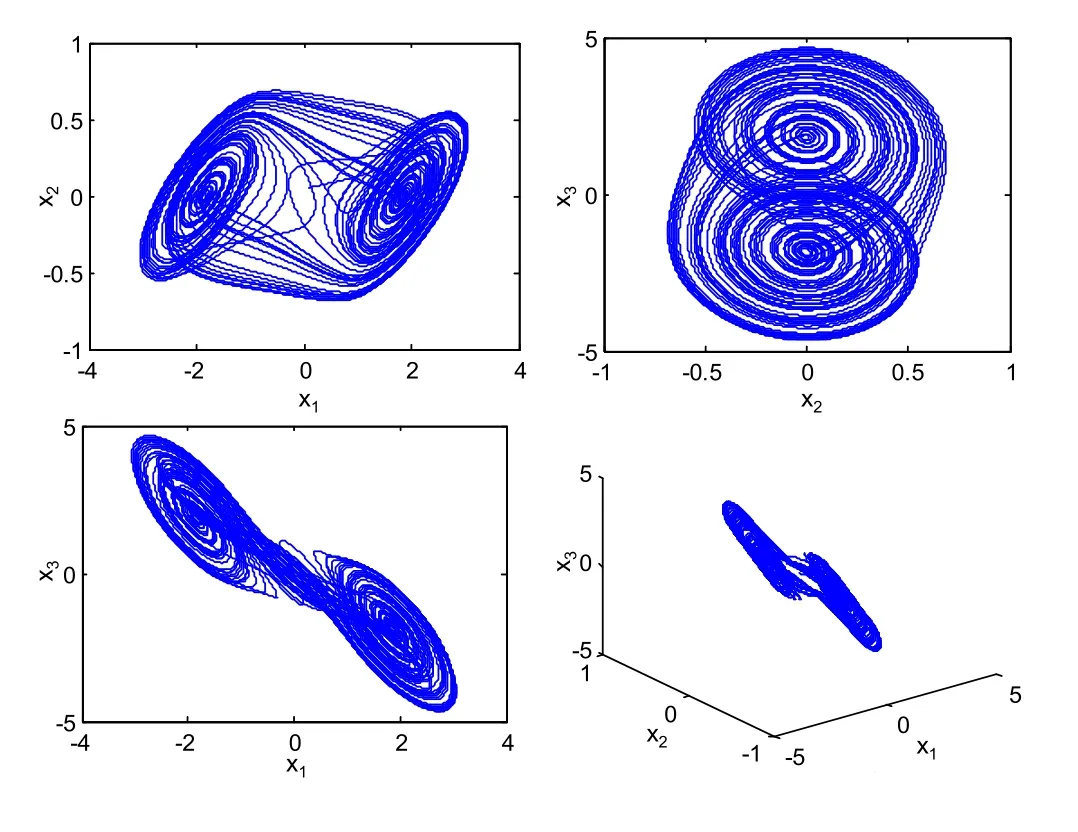
图1 Chua’s电路的混沌吸引子相图

根据式(7),构造响应系统.=T+ATy+T+g(y)+T+Lε+T+DU,U=-mtanh(Kε),=(Kε)Ttanh(Kε)。
任选初值为:驱动系统(1 2 5),响应系统(-1 -2-3 -4)。m的初值选为15,选取步长0.000 1进行仿真,则误差和m的动态演化曲线如图2和图3所示。

图2 广义误差e1和e2随时间变化的动态曲线

图3 误差e3和自适应量m随时间变化的动态曲线
3 结论
综上所述,笔者研究了与已知系统不同阶且满足响应系统阶数大于驱动系统阶数的广义同步系统构造理论及其应用,所提方法适用范围广。构造的系统中带有控制器,当系统的非线性项满足一定条件时,不论系统处于何种状态,都可以实现广义同步;自适应律的设计,使得所构造系统可以在线调整参数误差,有效地实现与驱动系统的同步。用Lyapunov稳定性理论给出了严格证明,并用蔡氏电路进行仿真,结果表明该方法是有效的,并且具有很好的鲁棒性。这将进一步提高广义同步在保密通信中应用的抗破译性,提高保密通信的安全性。
