超高性能混凝土抗压性能尺寸效应研究

2022-11-17邱宇康胡泽堃云葛心宇

四川水泥 2022年10期

赵康邱宇康胡泽堃云葛心宇陆鹏刘峰

（南京林业大学，江苏南京 210037）

0 引言

超高性能混凝土（以下简称为“UHPC”）是近年来出现的一种高强度、高刚度的材料，同时也具有优异的韧性以及耐久性，在一些大型大跨结构中有着较为广阔的应用前景。

尺寸效应是指材料的力学性能具有尺寸相关性，即在不同尺寸下其力学性能显示出一定的差异性。混凝土的力学性能与多种因素相关，除原材料特性、配合比和养护制度等外，试件尺寸的影响也是不可忽略的。1925年，Gonnerman[1]就发现了尺寸效应在混凝土材料中的存在，即混凝土的强度往往随着试件尺寸增大而呈现出一定规律的降低。在土木、桥梁和水利工程等领域，通常都是大型结构，实验室中所测强度值并不能反映其真实强度[2]。因此研究尺寸效应对混凝土抗压性能的影响尤为必要。

混凝土的抗压强度包括立方体、棱柱体和圆柱体抗压强度。在20世纪就有众多学者对混凝土抗压强度的尺寸效应进行了大量实验研究，Neville[3]对抗压强度介于13～48MPa，尺寸为70mm、125mm和150mm的立方体试件进行测试发现，小尺寸试件抗压强度明显高于大尺寸试件。Malhotra[4]则发现对于强度为7～48MPa的混凝土试件，150mm×300mm圆柱体试件的抗压强度相对于100mm×200mm试件普遍偏低。Yi等[5]对圆柱体及立方体试件抗压强度的尺寸效应进行了研究，其结果与尺寸效应理论吻合良好。

苏捷[6][7]研究了骨料对混凝土抗压性能尺寸效应的影响，结果表明，掺加粗骨料的混凝土试件抗压强度尺寸效应更明显。混凝土的宏观力学性能主要受界面过渡区的影响，粗骨料越多，则界面过渡区越多，而混凝土受压破坏时往往从界面过渡区开始。根据随机强度尺寸效应理论，骨料越多的混凝土试件有更多的薄弱面，因此其发生失效破坏概率更大，表现为尺寸效应更显著。同时其也对含粗骨料的高强混凝土的尺寸效应进行了测试[8]，结果表明高强混凝土依然存在尺寸效应且较明显，其结果与大多数研究者的实验结果都吻合。

1 不同钢纤维掺量对抗压强度的影响

本文首先分析不同钢纤维掺量下UHPC抗压性能，然后选择合适的纤维掺量进行尺寸效应测试研究。

本项目使用的UHPC是一种由苏博特公司商品化的产品SBT-HDC。钢纤维掺量按体积分数来控制，试件尺寸为100mm×100mm×100mm，钢纤维掺量分别为0%、1%、2%。测试仪器为江宁结构实验室300t压力试验机，加载速率为0.5mm/min。

当钢纤维掺量为0%时，抗压强度为72.2MPa、82.0MPa、94.6MPa，平均值为82.9MPa，破坏模式为接近45°角的锲型破坏，损坏的碎片处于分崩离析状态，呈脆性破坏，现场可以听到响亮的炸裂声。当钢纤维掺量为1%时，抗压强度为120.3MPa、113.6MPa、122.5MPa，平均值为118.8MPa，破坏时试件出现碎屑，同时由于钢纤维的作用试件破坏时整体还间断连接，呈延性破坏。当钢纤维掺量为2%时，抗压强度为146.4MPa、136.1MPa、140.8MPa，平均值为141.1MPa，破坏时相比较而言破碎的部分变少，间断的部分可以看到钢纤维。

不同钢纤维掺量对应的UHPC的抗压强度见表1。由表1可以看出，钢纤维的掺量对UHPC抗压强度影响较大，相比于0%的掺量，1%的掺量其抗压强度增长了40%、2%的掺量其抗压强度增长了70%。未掺入钢纤维时，试件内部存在着较多微裂纹及其他缺陷，试件受荷承受压应力时，非受荷方向承受与压应力方向垂直的拉应力，在拉应力作用下，试件内部缺陷最先达到极限受荷状态从而成为裂缝开展端，在无纤维约束的情况下，裂缝快速发展直至混凝土试件破坏，使得试件强度不高。

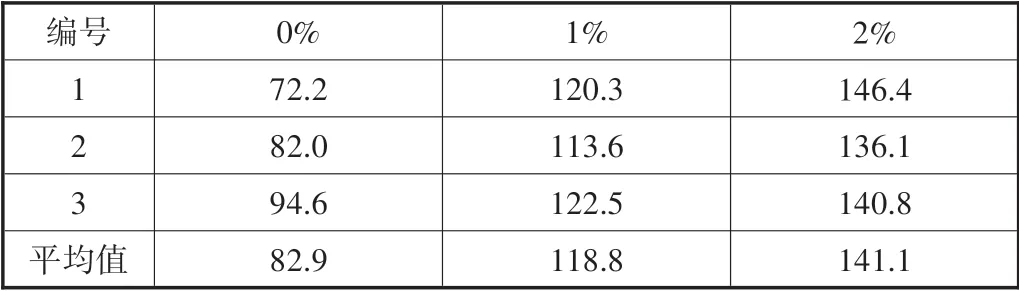
表1 不同钢纤维掺量的UHPC的抗压强度（单位：MPa）

当试件内部掺入钢纤维后，其乱向分布于试件内部形成三维骨架与UHPC基体共同承担外力。一方面，钢纤维能够约束混凝土的横向变形，起到“环箍效应”作用；另一方面，试件内部缺陷处裂纹开展时钢纤维能够有效桥接微裂缝，抑制其开展，随着裂缝继续发展，钢纤维依然能够传递应力从而有效抵挡外力。在此过程中，钢纤维与基体不断发生粘结滑移，钢纤维与基体间良好的粘结力使其消耗了大量能量，因此试件抗压能力大大提高。随着钢纤维掺量的增加，纤维平均间距减小，更多的纤维能够承受荷载并抑制微裂缝开展，其在一定程度上能够提高UHPC的延性，使得上述作用进一步增强，纤维掺量越大，试件的延性越明显[9]。

2 尺寸效应研究

2.1 不同尺寸的立方体抗压荷载位移关系及其抗压强度

选取2%的纤维掺量继续拌和成型不同尺寸的立方体试件，其边长分别为70.7mm、100mm、150mm。试件表面基本较为光滑，仅有一些气孔，试件尺寸越大，气孔出现概率越大。各边长立方体抗压荷载位移关系见图1～图3。

图1 边长70.7mm的立方体抗压荷载位移关系

图2 边长100mm立方体抗压荷载位移关系

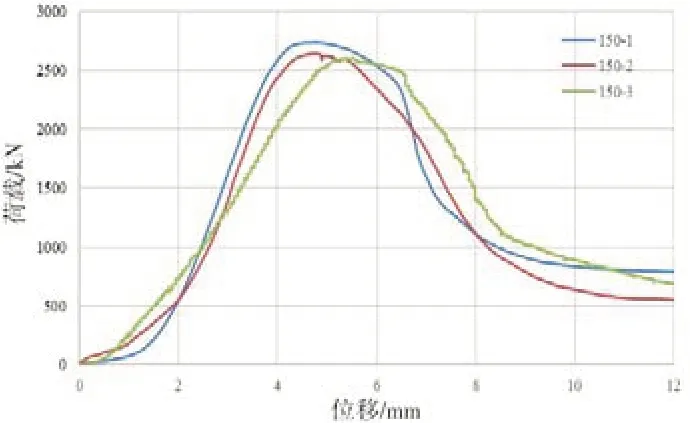
图3 边长150mm立方体抗压荷载位移关系

边长为70.7mm的试件抗压荷载为701.5kN、689.3kN、696.8kN时，其抗压强度分别为140.3MPa、137.9MPa、139.4MPa。

边长为100mm的试件抗压荷载为1333.2kN、1425.7kN、1353.6kN时，抗压强度分别为133.3MPa、142.6MPa、135.4MPa。整体上看，抗压强度略微比70.7mm边长试件小一些。

边长为150mm的试件抗压荷载为2734.6kN、2644.8kN、2603.4kN时，其抗压强度分别为121.5MPa、117.5MPa、115.7MPa。整体上看，其抗压强度比70.7mm、100mm边长试件更小一些。

2.2 尺寸效应分析

尺寸效应受众多因素的影响，其产生基础为不同尺寸试件中的缺陷差异。统计尺寸效应理论认为，由于大尺寸试件中存在更多的缺陷，因此其发生失效破坏的可能性大于小试件。UHPC中大尺寸试件往往存在更多的微裂纹和孔隙，因此其缺陷相比小尺寸更多，发生强度下降的可能性也大大提高。根据断裂力学学说，试件破坏时的临界应力与裂纹长度的平方根成反比，而大尺寸试件往往裂纹长度大于小试件，因此其临界应力将低于小试件。

表2列出了各个尺寸试件的立方体抗压强度数据，可以看出边长为70.7mm、100mm、150mm的试件抗压强度分别为139.2MPa、137.1MPa、118.3MPa，随着尺寸的增大，强度代表值降低。