2021年高考数学试题综合难度比较分析
2022-11-16杨正朝贵州师范大学数学科学学院550025
杨正朝 (贵州师范大学数学科学学院 550025)
1 问题提出
2019年《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》强调科学设置试题难度,命题要符合相应学业质量标准,体现不同考试功能.[1]随后,教育部颁布《普通高等学校招生全国统一考试大纲》,明确提出高考应具有适当的难度.[2]可见,试题难度不仅是教育部门关注的重点,也是社会关注的焦点.
为了更好地测量试题难度,文[3]对鲍建生课程难度的综合难度模型进行改良,并用于测试中韩两国高考试题的难度差异.文[4]基于文[3]的综合难度模型,增加了条件含量、阅读量两个因素,并以此为框架,对2016—2020年高考数学(理科)全国卷中的“统计与概率”进行难度对比分析.文[5]以文[3]综合难度模型为基础,以是否含参、运算水平、推理能力等难度因素为测评框架,对2019和2020年高考理科数学全国Ⅱ卷进行难度分析.可见,近年来对高考试题进行难度分析和比较,逐渐成为了数学教育的热点话题.因此,本研究以2021年高考试卷为例,对其综合难度进行分析对比,以便更好地为数学教学和高考命题提供建议.
2 研究设计
2.1 研究对象及方法
2021年高考试卷主要由三类组成:一是新高考试卷;二是文理不分科的自主命题;三是高考全国卷.研究以2021年全国理科(甲乙卷)、新高考Ⅰ卷和浙江卷共四套试卷为对象,进行综合难度分析,数据结果借助SPSS和Excel分别绘制条形图和雷达图,以便能够直观地进行比较分析.
2.2 研究工具
(1)综合难度模型
本研究基于文[3]的综合难度模型,以该模型的七个难度因素为框架,进行水平划分.各难度因素按A~G逐一进行编码,每个因素水平都分2~4级,依次赋值1~4,相关编码及赋值如表1所示.
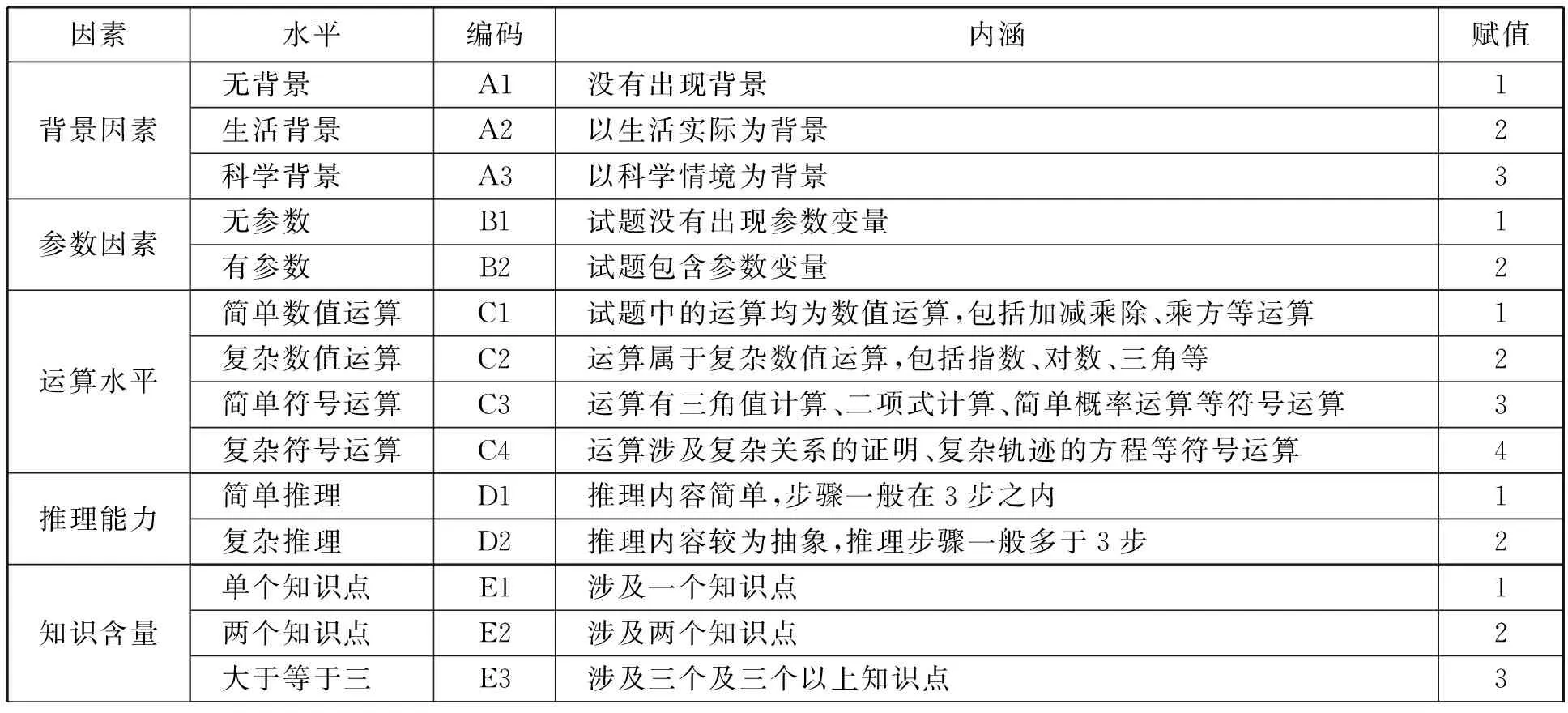
表1 综合难度模型水平划分及赋值

表1 综合难度模型水平划分及赋值(续)
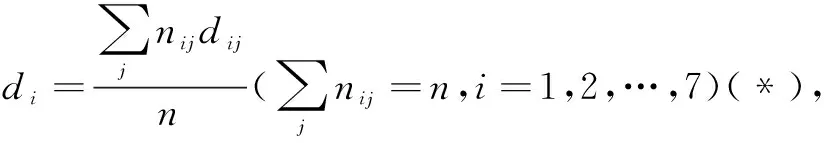
(2)示例分析
例(2021年全国乙卷第10题)设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则( ).
A.a
难度水平分析该题编码为:A1无背景(题目为纯数学知识),B2有参数(含有参数变量a,b),C3简单符号运算(包含求导等符号运算),D2复杂推理(推理较为抽象,步骤在3步以上),E3两个知识点(包括零点、极值点、单调性等知识),F1顺向思维(按题目条件直接求解问题),G2运用(运用函数与导数相关知识求解).
3 研究结果
根据表1水平划分和赋值标准,对2021年四套试卷中的试题进行分析,得出相关数据.其中,百分比为各因素水平题目数除以试卷试题总数(全国甲乙卷均为23个题,而新高考Ⅰ卷和浙江卷均为22题),例如全国甲卷无背景A1:19÷23=82.6%,浙江卷无参数B1:9÷22=40.9%.并结合公式(*)计算各因素的综合难度系数,最终数据结果如表2所示.
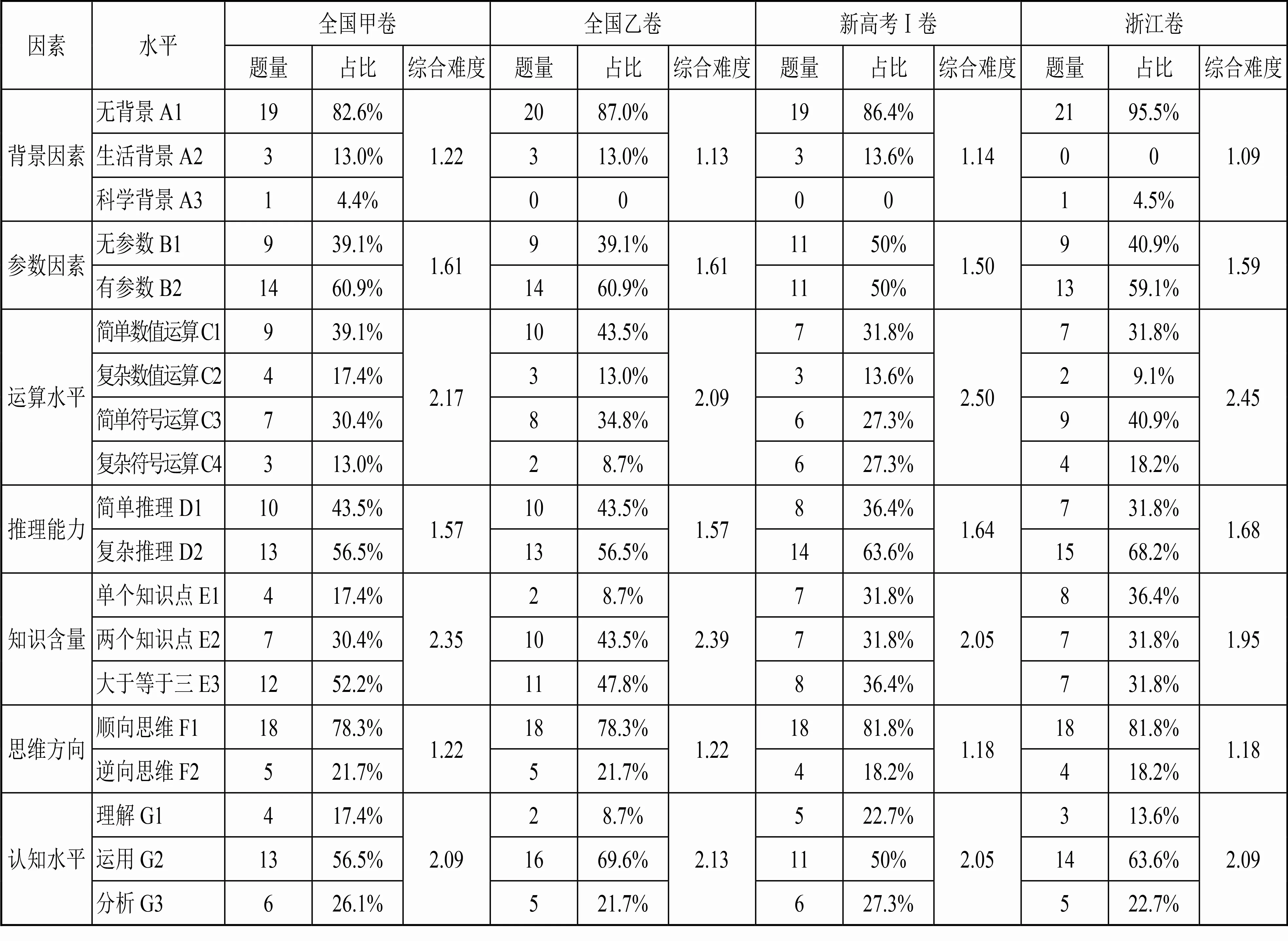
表2 四套试卷的试题综合难度系数统计
为了能够生动地刻画不同试卷的7个因素情况,通过表2数据,利用SPSS绘制条形图,对四套试卷进行比较分析.对于整套试卷的综合难度系数,利用Excel绘制雷达图做整体性分析.
3.1 背景因素分析
由图1可知,在生活背景方面,全国甲乙卷和新高考Ⅰ卷均有考查到,而且比重均为13.0%左右,浙江卷没有涉及到生活背景的考查;在科学背景上,仅有全国甲卷和浙江卷考查到,分别为4.4%和4.5%,其余两套试卷都为0.可见,全国统一命题的试卷比较注重有背景的考查,而浙江卷相对较少.
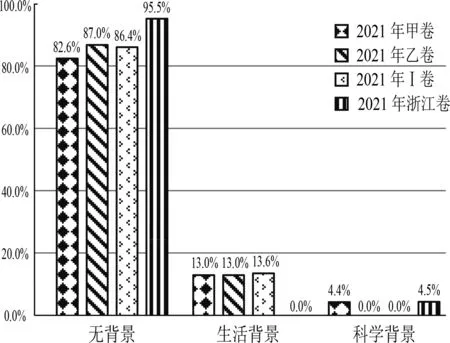
图1
3.2 参数因素分析
由图2可以发现,在有参数方面,全国甲乙卷考查占比较高,均为60.9%,浙江卷次之,为59.1%,新高考Ⅰ卷最低,为50%.试题含有参数,在一定程度上要比无参数的试题抽象.
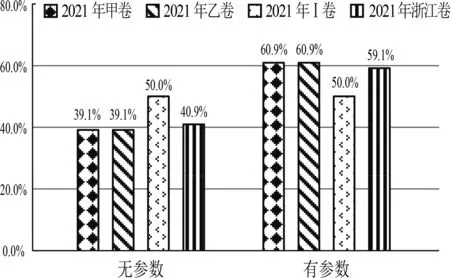
图2
3.3 运算水平分析
由图3可知,四套试卷对于运算因素的四个水平都有全面考查到,但是分布不均衡.在简单数值运算上,全国乙卷为43.5%,比重最大,其次全国乙卷,为39.1%,最低的是新高考Ⅰ卷和浙江卷,均为31.8%;在复杂数值运算上,四套试卷的差别不大;在简单符号运算方面,浙江卷>全国乙卷>全国甲卷>新高考Ⅰ卷;在复杂符号运算上,新高考Ⅰ卷比重最高,为27.3%,运算难度较大,浙江卷次之,为18.2%,全国甲乙卷较低.从整体来看,四套试卷都侧重于考查简单数值和简单符号运算,二者之和占一半以上.
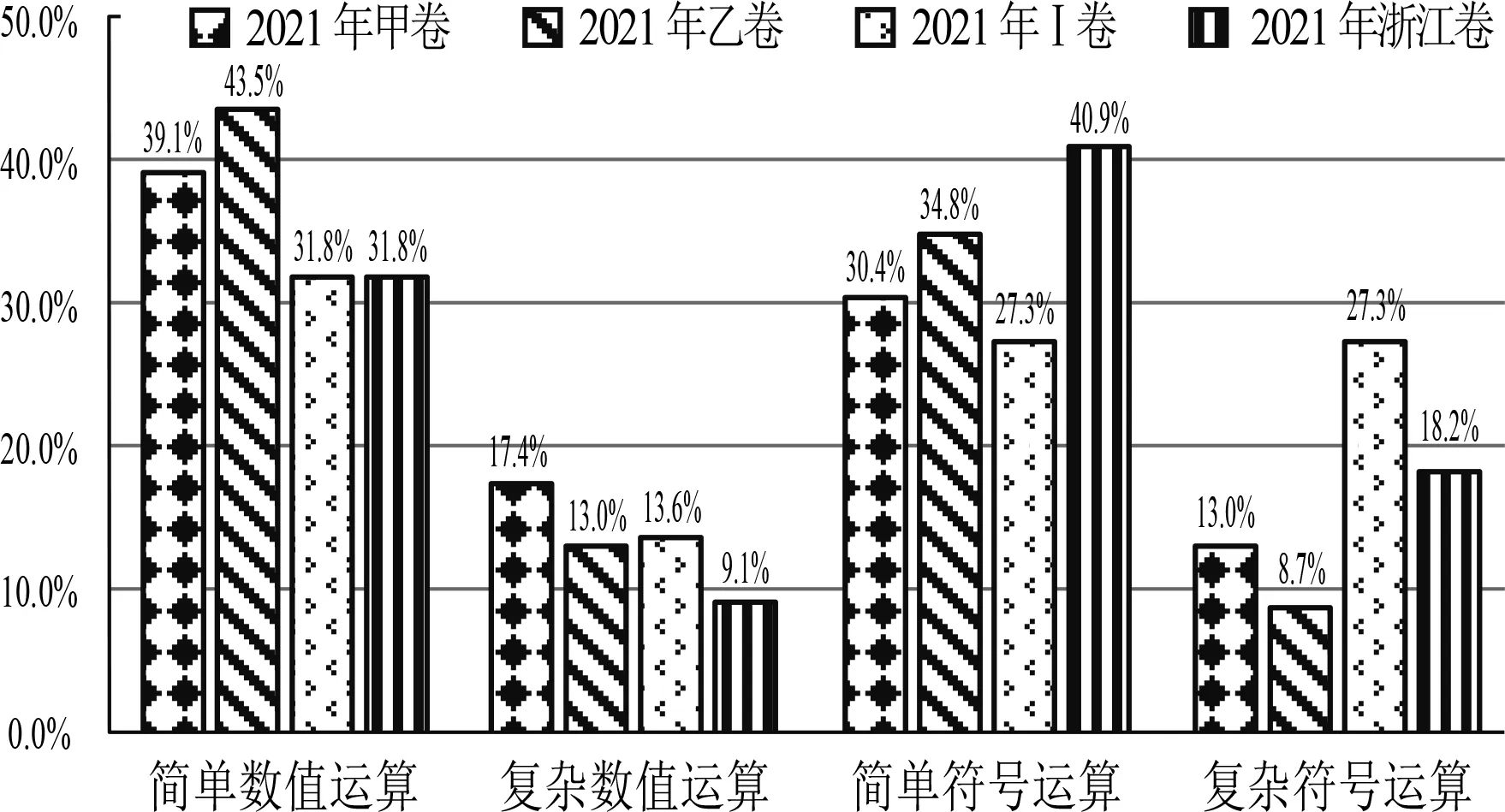
图3
3.4 推理能力分析
由图4可知,四套试卷重点考查复杂推理.在复杂推理方面,浙江卷比重最高,为68.2%,新高考Ⅰ卷次之,最低为全国甲乙卷,均为56.5%.可以看出,浙江卷在逻辑推理方面,运算步骤多,要求较高的逻辑推理能力.
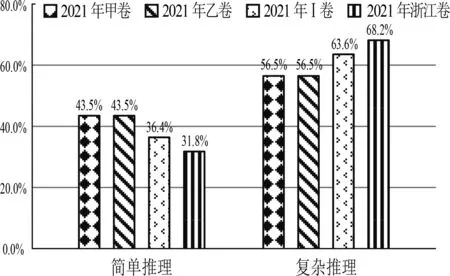
图4
3.5 知识含量分析
由图5可以看出,对于知识含量因素三个水平的考查,四套试卷都有考查.在单个知识点方面,浙江卷最高,比重为36.4%,其次是新高考Ⅰ卷31.8%,全国甲卷为17.4%,全国乙卷最低,仅有8.7%;在两个以上知识点的考查上,全国乙卷比重较高,其次是全国甲卷,新高考Ⅰ卷和浙江卷紧随其后.从整体来看,浙江卷和新高考Ⅰ卷对三个水平考查相对均衡,而全国甲乙卷较为偏向于两个知识点以上的考查,考查知识点更为综合.
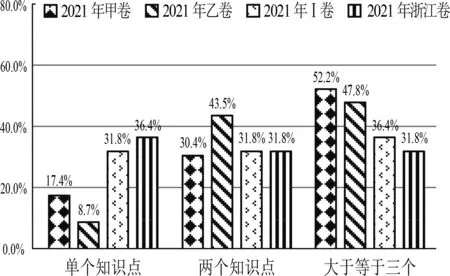
图5
3.6 思维方向分析
从图6可知,四套试卷都倾向于考查顺向思维.在顺向思维上,浙江卷和全国Ⅰ卷占比最大,均为81.8%,其次是全国甲乙卷,都是78.3%,四套试卷的顺向思维考查占比都在三分之二以上,这也体现了顺向思维符合学生思考方向,考查难度较适宜.在逆向思维上,四套卷的比重都在20%左右,其中,全国甲乙卷比重较高一些.适当增加逆向思维的试题,能够考查学生发散思维,对于不同层次的学生有良好的区分效果.
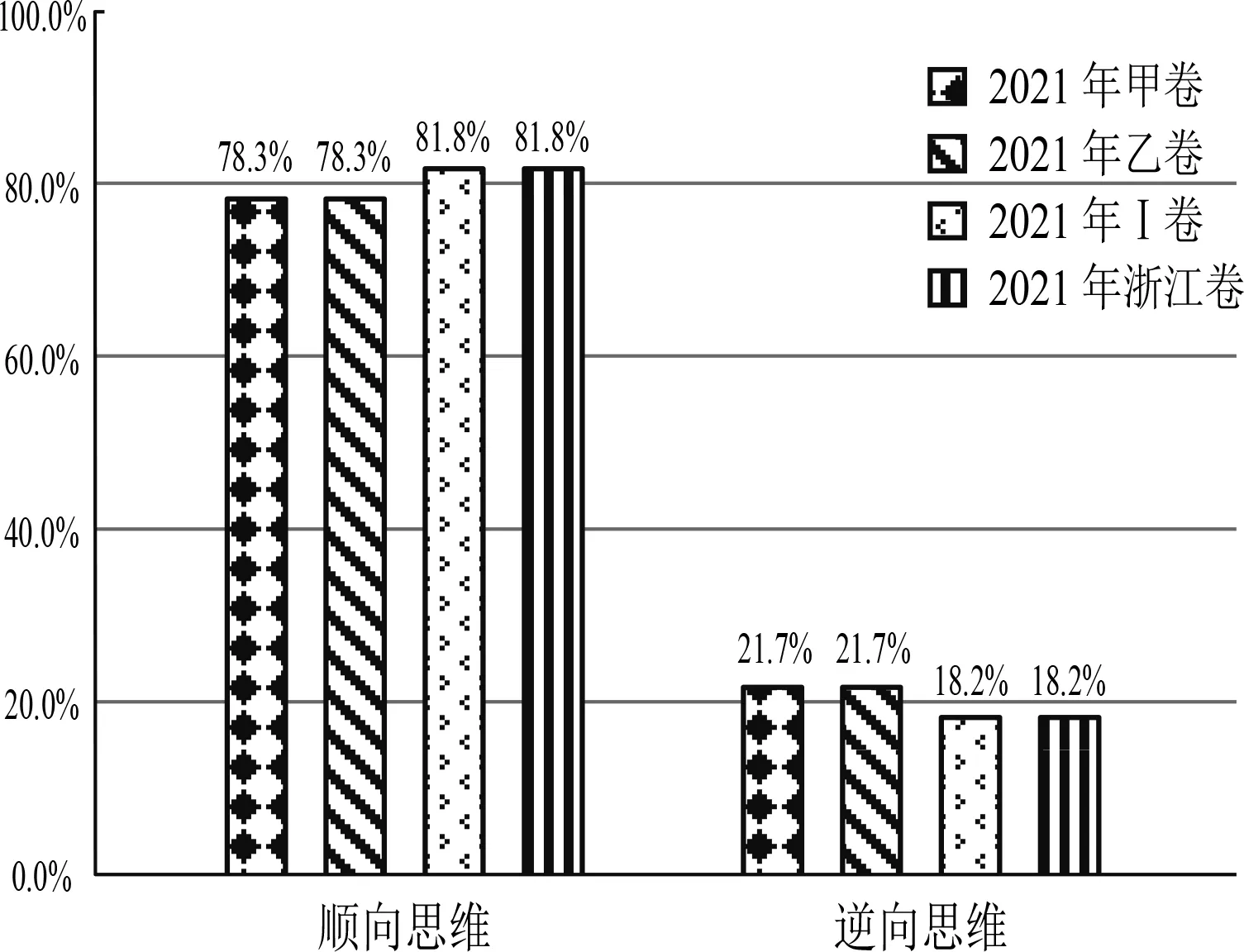
图6
3.7 认知水平分析
由图7可以看到,四套试卷对于认知因素的三个因素都有考查到,尤其是对于运用水平的考查,比重都比较高.在理解水平上,新高考Ⅰ卷考查较多,占22.7%,全国乙卷最低为8.7%;在运用水平方面,四套试卷占比均为一半以上,其中全国乙卷最高,其次是浙江卷,全国甲卷和新高考Ⅰ卷紧随其后;在分析水平上,新高考Ⅰ卷>全国甲卷>浙江卷>全国乙卷,分析水平侧重于考查学生综合运用已有知识、方法等分析和解决问题的能力.
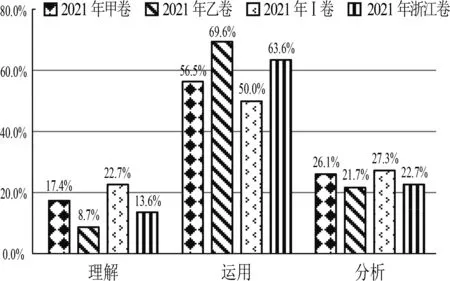
图7
3.8 综合难度分析
结合表2数据,利用各难度因素权重值ki以及公式(** ),计算出四套试卷的综合难度系数,统计结果如表3.为了直观形象地刻画各难度因素水平,绘制出雷达图8.

表3 综合难度系数表
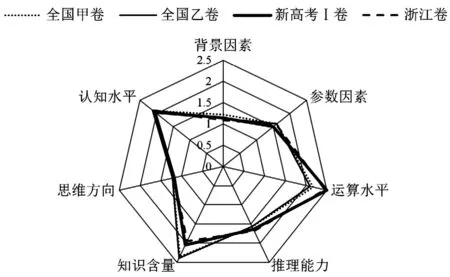
图8
由表3可知,四套试卷的综合难度系数从高到低依次排序,分别为:浙江卷>新高考Ⅰ卷>全国甲卷>全国乙卷.浙江卷相对来说,难度较大一些,全国统一命题的试卷差异不大.由于综合难度系数不止上述7个因素,因此,该数据在此难度模型下,仅供参考.
从图8可知,一方面四套试卷在背景因素、参数因素、推理能力、思维方向、认知水平五个方面差异不大,其余两个难度因素有所差别,但差距不大,这体现了高考试卷保持一定的稳定性和一致性.另一方面,四套试卷在运算水平、知识含量两个难度因素上综合难度系数均高于1.9,体现了试卷在运算能力和知识点综合运用上,考查难度较大.
4 研究结论
4.1 相对于自主命题而言,全国统一命题更关注背景因素的考查
上述试卷中,前三套均为全国统一命题试卷,通过数据分析比较,不难发现,其显著的特点是注重背景因素的考查,背景即课标中的情境.反观浙江卷,对于背景因素的考查较少.一方面试题以生活和科学设置情境,贴近现实,符合学生认知水平.例如,2021年全国甲卷的第4题以“青少年视力”为背景设计数学问题.近年来,随着互联网的发展,青少年视力问题变成公众关注的焦点,以此问题为切入点,不仅能够引起学生的重视,而且考查学生综合运用已学知识解决实际问题的能力,培养学生应用能力.另一方面“情境”二字多次出现在新课标,频次较高,这也体现了情境设置在高中数学教学中的重要性,情境作为数学问题的载体,也能够更好地体现育人的功能.例如,2021年全国乙卷第6题以“北京冬奥会志愿者”为背景,考查学生对计数原理和组合的运用,同时,也能够激发学生的志愿精神.
4.2 浙江卷综合难度系数偏高,学生应具备一定的数学基础
通过上述对试卷综合难度系数的分析,研究表明,浙江卷在考查难度上要高于其他三套试卷.但是通过试卷的试题分析,能够发现,统一命题的全国卷中,存在着许多基础题,因为统一命制的试卷面向的是多个省份,各省份教育和经济水平不一致,因此,在试卷难度上要保持平衡,注重考查学生的数学基础知识和基本数学素养.而浙江卷由于面向的是浙江省省内学生,加上浙江省教育水平本身比较好,所以在试卷命制上更加注重中、高水平知识的考查,导致难度会有所加大.尽管考查的内容一致,但是命制的出发点不一样,也就导致了试题难度上难免会有所差异.因此,教学中要注重数学基础的培养,如果学生不具备一定的数学基础,在成绩上很难有所提升.
4.3 四套试卷都重视运算能力和知识含量的考查
对于运算水平和知识含量的考查,两者的难度系数都在1.9以上.一方面数学运算作为一种特殊的演绎推理,是处理数学问题、得到正确结果的基本途径.[7]同时,数学运算也是数学六大核心素养之一,可见,在命题上加强对学生运算能力的考查就显得理所当然.数学运算无论是在数学学习,还是现实生活中,是应用最为普遍的关键能力,而且也是衔接其他学科的重要纽带.另一方面知识含量体现了学生对知识点的掌握情况,试题的知识点融合得越多,越考查学生对知识的全面掌握程度,也考查学生对多个知识点的综合运用能力.现实社会中,面对的问题纷繁复杂,如果对于综合性的数学问题都一筹莫展,难以解决,那么踏入社会,学生只会举步维艰.
4.4 相比其他试卷,新高考试卷更加重视知识的综合运用
新高考在试卷结构和题型上发生了重大变化,但是试题难度与其他试卷相比,差异性不大.新高考增设了多选题,一是多选题形式新颖,考查的内容更为全面综合.例如,2021年新高考Ⅰ卷第9题,考查学生对统计中平均数、中位数、标准差等内容的理解,辨析它们的差异,考查内容全面,难度并不大,这就要求学生在日常学习中,掌握基础数学知识,养成勤于归纳总结的习惯,才能正确解决此类问题;二是多选题的设置,对不同层次的学生更具区分效果.多选题的得分机制是“全选对得5分,部分选对得2分,有选错的得0分”,其一方面突显高考的人性化,增加学生的得分机会.另一方面更好地区分不同层次的学生,使高考起到更为科学的人才选拔作用.
5 研究启示
高考作为学生学业质量水平检测的重要手段,同时也肩负着人才选拔的重任.为此,研究通过高考试卷综合难度分析,旨在为数学教学和命题提供参考.首先,合理调节试卷难度,使其更具区分效果.这里指的区分效果并不是每个题都要提升难度,而是要求试卷中的极个别试题在命制上要有区分度.比如试卷的选择题或填空题最后两题,可以适当提升难度,这样能够更好地体现人才选拔的目的,对不同层次的学生起到更好的区分效果.其次,夯实基础知识,落实“四基”“四能”.新课标强调“四基”“四能”,其立足于基础知识的学习,才能够有更加长远的发展.通过试卷分析能够发现,高考中大多数试题是以基础知识为方向来命制的,尤其是全国统一命制的试卷,更加体现这一特点,这就要求在实际教学中,注重基础知识的理解和运用,夯实基础数学知识,提高自身的分析和解决问题能力.最后,加强开放性题型的命制,全面考查学生数学素养.开放性题型形式灵活,对学生能力要求更为全面和综合,能在一定程度上考查学生的创新意识.在教学过程中,要加强对学生探究意识的培养,让学生在情境中,积极地参与问题提出和问题解决.
