齿轮螺旋线修形优化研究
2022-11-16司国雷陈君辉王嘉磊李思作
司国雷, 李 侃, 陈君辉, 王嘉磊, 朱 旭, 李思作
(1.四川航天烽火伺服控制技术有限公司, 四川 成都 610000;2.火箭军装备部驻成都地区第二军事代表室, 四川 成都 610000)
引言
发动机是工业系统的核心动力源之一,能将电能转化为机械能,实现动力的传输。作为发动机关键组件的啮合齿轮应具有高速、均载、振动冲击小等特性。齿轮修形作为减振均载、实现啮合平稳过渡的主要手段被广泛使用。近年来,各高校、科研院所等对于此展开了深入的研究。邓小禾[1]针对非对称齿轮的齿廓采用渐开线倾斜修形,降低了齿轮的最大磨损量,提高了齿轮的抗疲劳能力,并且研究表明齿轮中心线空间角度错位会严重影响齿轮的啮合性能。张沁薇[2]建立了斜齿轮热弹流润滑模型,研究了不同参数对齿轮润滑的影响,通过减小载荷,增大转速,降低油液温升有利于油膜的形成,极大提高抗胶合能力。杨丽等[3]运用Kriging模型和遗传算法对齿轮减振进行修形优化, 解决了计算啮合刚度大、精度低等问题,显著降低了齿轮振动。史朋真[4]在考虑中心线偏差及支撑装置变形的情况下,运用带鼓形的螺旋线修形,针对齿轮进行多目标优化,修形后偏载现象得到改善,接触应力降低22%以上。CHEN Zaigang等[5]通过啮合刚度计算模型分析出齿廓变位对啮合刚度、载荷分配系数具有明显的影响。FAGGIONI等[6]和MA等[7]分析了不同修形量下齿轮的啮合刚度和传递误差,结果表明合理的齿顶修形能够显著改善齿轮振动。随着仿真优化计算的兴起,采用虚拟验证是工程常用手段,能够快速验证齿廓修形和齿向修形对于齿轮的影响,从而对齿轮有针对性的进行优化,改善传动状态,提高啮合质量[8-10]。
1 齿向修形原理
齿轮承受载荷后齿轮轴会发生弯曲和扭转等弹性变形,从而偏离原始位置,同时齿轮、壳体、轴承等制造误差将会引起齿轮齿向接触不均匀,造成齿轮啮合过程存在啮合歪斜度,在啮合轴线和垂直平面内存在误差,类似于斜齿轮啮合,呈螺旋状态。通过采用螺旋线修形修正啮合歪斜度,可以在一定程度纠正误差,达到减振降噪的目的。另一方面,如果一对啮合的齿轮齿宽不等,将会产生棱边效应,也会影响齿轮承载能力的提高和使用寿命。通过齿向修形的最主要目的是保证机件在最大螺旋线总偏差的情况下互相啮合的齿轮不发生端点接触——相切而不相割,减少棱边效应;同时还应保证在不倾斜或少量倾斜的情况下,最大限度地减少单位齿宽上的载荷[11]。
通过齿向修形使其恢复到理论啮合位置,达到最佳接触斑点,可以降低因各种因素引起的轴线不平度,降低螺旋线载荷分布系数KHβ,减少偏载提高承载能力,齿向修形原理如图1所示。
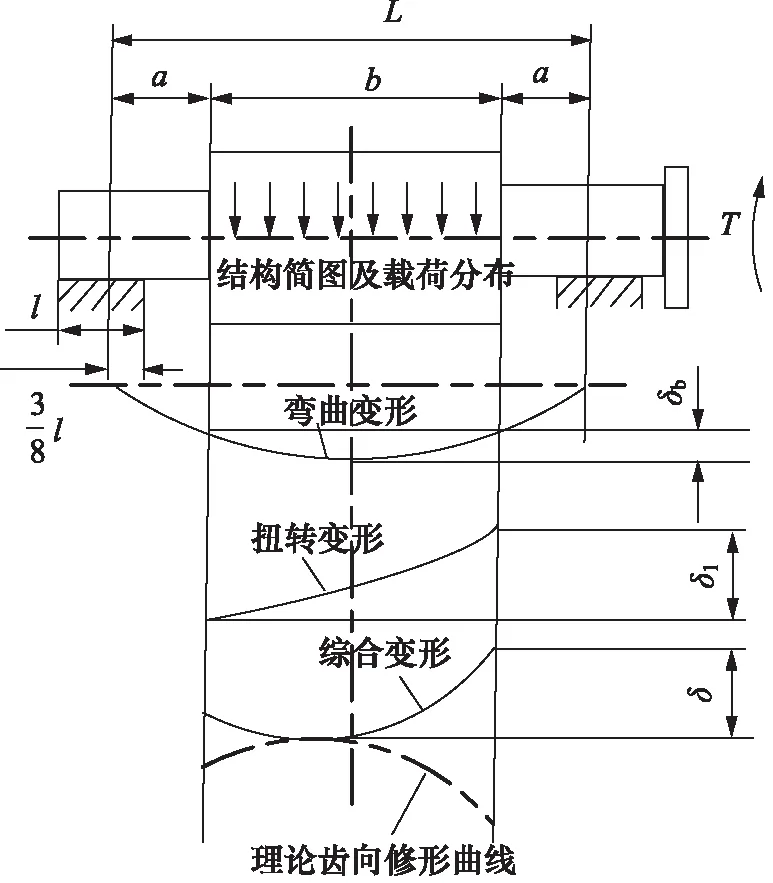
图1 齿向修形原理Fig.1 Principle of tooth shaping
齿向载荷的分布与齿轮的受载情况相关,如图2所示。
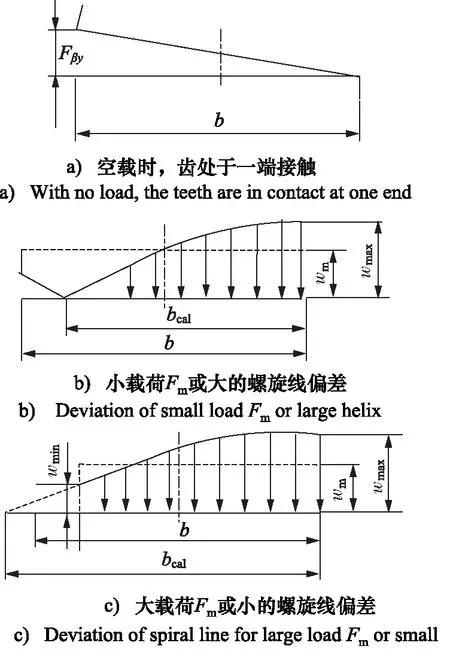
图2 载荷分布模型Fig.2 Load distribution model
螺旋线载荷分布系数KHβ为:
(1)
其中,KHβ的计算方式与载荷在齿宽方向上的受力宽度相关,分别如式(2)和式(3):
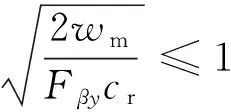
(2)
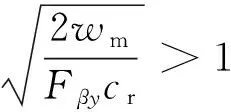
(3)
单位齿宽平均载荷为:
(4)
啮合综合刚度为:
cr=(0.75εα+0.25)c′
(5)
跑合后的螺旋线偏差量为:
Fβy=Fβx-yβ=Fβxxβ
(6)
本研究的齿轮受载情况接触良好,则:
fβx=1.33fsh+fma
(7)
式中,fsh—— 综合变形产生的啮合螺旋线偏差分量
fsh=wmfsh0
(8)
式中,fsh0—— 单位载荷作用下的啮合螺旋线偏差
在进行修形的情况下:
fsh0=0.012γ
(9)
对于直齿修形齿,在功率不分流的情况下,小齿轮结构尺寸系数γ为:
(10)
式中,KHβ—— 螺旋线载荷分布系数
wmax—— 单位齿宽最大载荷,N/mm
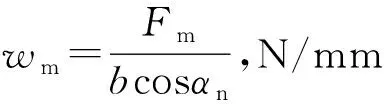
Fβy—— 跑合后啮合螺旋线总偏差,μm
cγ—— 啮合综合刚度,N/(mm·μm)
bcal—— 计算齿宽,mm
b—— 实际齿宽,mm
Fm—— 圆周力(名义外载荷),N
Ft—— 切向力,N
KA—— 使用系数
KV—— 动载系数
c′ ——单对啮合刚度,N/(mm·μm)
εα—— 端面重合度
xβ—— 螺旋线跑合系数
yβ—— 螺旋线跑合量,μm
Fβx—— 初始啮合螺旋线总偏差,μm
fsh—— 综合变形产生的啮合螺旋线偏差量,μm
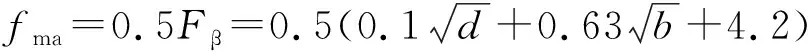
d—— 分度圆直径,mm
fsh0—— 单位载荷作用下的啮合螺旋线偏差,μm·mm·N-1
γ—— 小齿轮结构尺寸系数
B*—— 功率分流系数,功率不分流时,B*为1
k′ —— 结构系数,对于C形刚性支撑结构,
k′=1.33
l—— 轴承跨距,mm
s—— 小轮齿宽中点至轴承跨距中点的距离,mm
d1—— 小轮分度圆直径,mm
dsh—— 小轮轴弯曲变形当量直径,mm
齿向修形中为保证载荷集中程度最小,主要对其进行螺旋线修形,该齿形包括四大要素:结构设计、鼓形量的确定、鼓形中心的选取以及螺旋线修形量的确定,具体如图3所示。
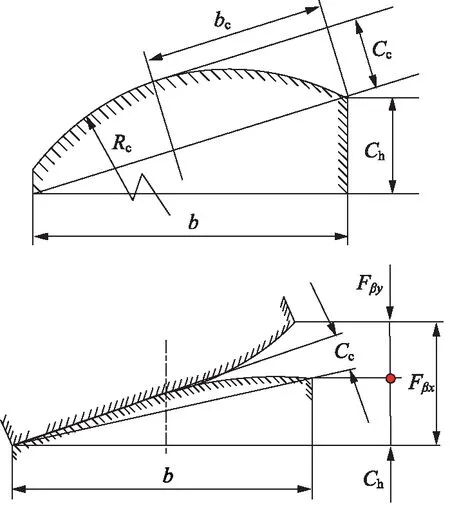
图3 带鼓形的螺旋线修形各结构参数Fig.3 Structural parameters of helix trim with drum
根据文献[8],为保证相切而不相割的条件,同时又能最大限度的提高齿轮的承载能力,则应同时满足式(11)~式(14)所规定的约束条件:
(11)
(12)
(13)
(14)
式中,bc——A点到鼓形中心之距,mm
Rc—— 鼓形半径,mm
Cc—— 鼓形量,μm
Ch—— 螺旋线修形量,μm
2 齿轮修形优化
2.1 基于KISSsoft的齿轮修形
在实际的啮合齿轮组设计过程当中,因其计算参数过程非常繁琐、复杂,按传统的基于设计手册的设计方法设计很难达到各种传动性能指标最优化的目标。采用传统设计方法,不但对设计人员自身经验、知识水平有较高要求,而且计算也容易出错。KISSsoft能够方便地实现齿轮设计、优化和评级,能够以极低的代价、在极短的时间取得理想的齿轮设计结果。
2.2 螺旋线修形优化流程
本研究采用KISSsoft软件进行螺旋线修形的优化仿真设计,具体步骤如下:
(1) 选定需要优化的啮合齿轮组并确定其传动工况,啮合齿轮组的关键参数如表1所示。
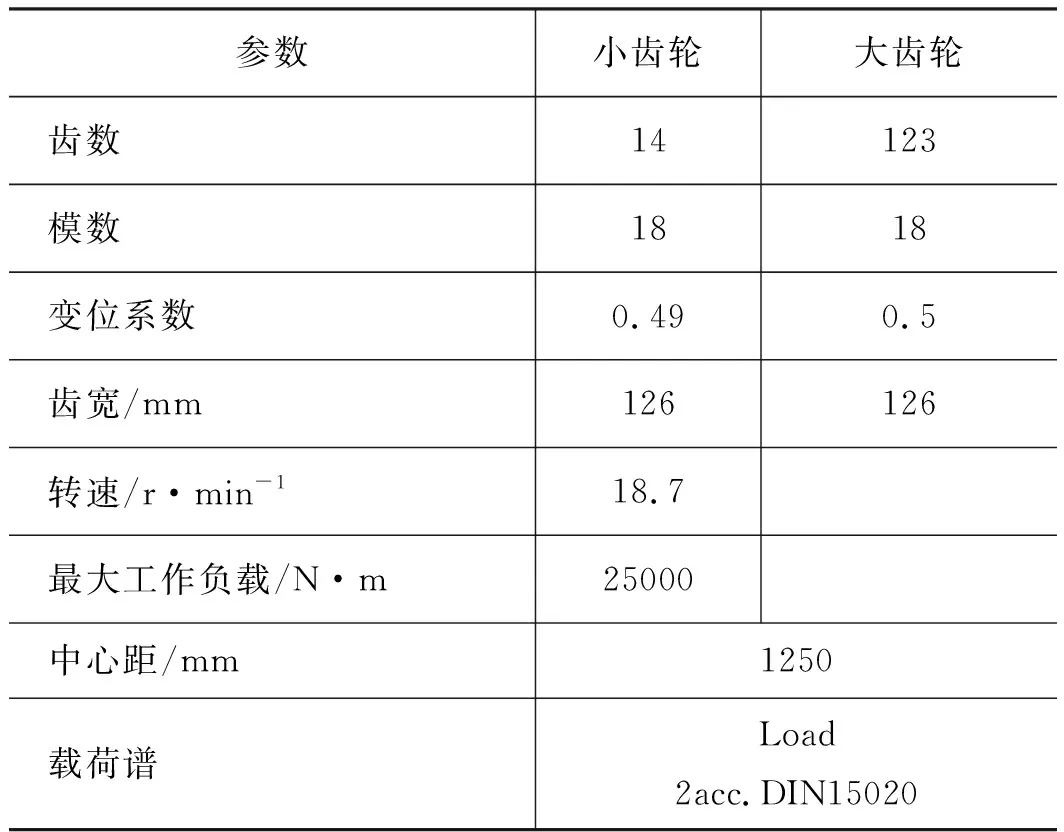
表1 啮合齿轮组参数Tab.1 Parameters of meshing gear
(2) 运用KISSsoft搭建轴系模型和啮合齿轮组模型,并设定结构参数及传动实际啮合条件;
(3) 仿真,获取啮合齿轮组初始滑动率、传动误差、油膜厚度、齿面应力分布以及螺旋线载荷分布系数等;
(4) 添加固定鼓形修形量25 μm,螺旋线修形量范围为-350~300 μm,每10 μm设置为一个增量步,获取相应条件下滑动率、传动误差、油膜厚度、齿面应力分布以及螺旋线载荷分布系数等,直到螺旋线载荷分布系数KHβ接近于1,停止优化,输出相对最优解;
(5) 运用KISSsoft多目标修形优化模块,设定螺旋线修形量范围,执行自动优化,对比步骤(4)及本步骤仿真结果,相互验证修形结果的正确性,同时使螺旋线修形量进一步靠近最佳值;
(6) 输出最佳值作为修形最终解。
3 结果分析
3.1 螺旋线修形对润滑油膜的影响
高转速条件下,相互啮合的轮齿之间形成流体动力润滑有利于降低磨损速率,延长齿轮使用寿命。流体动力润滑包括4种情况:“刚性 - 等黏”润滑(R-I润滑), “弹性 - 变黏”润滑(E-V润滑),“刚性 - 变黏”润滑(R-V润滑)以及“弹性 - 等黏”润滑(E-I润滑),润滑性质如图4所示。
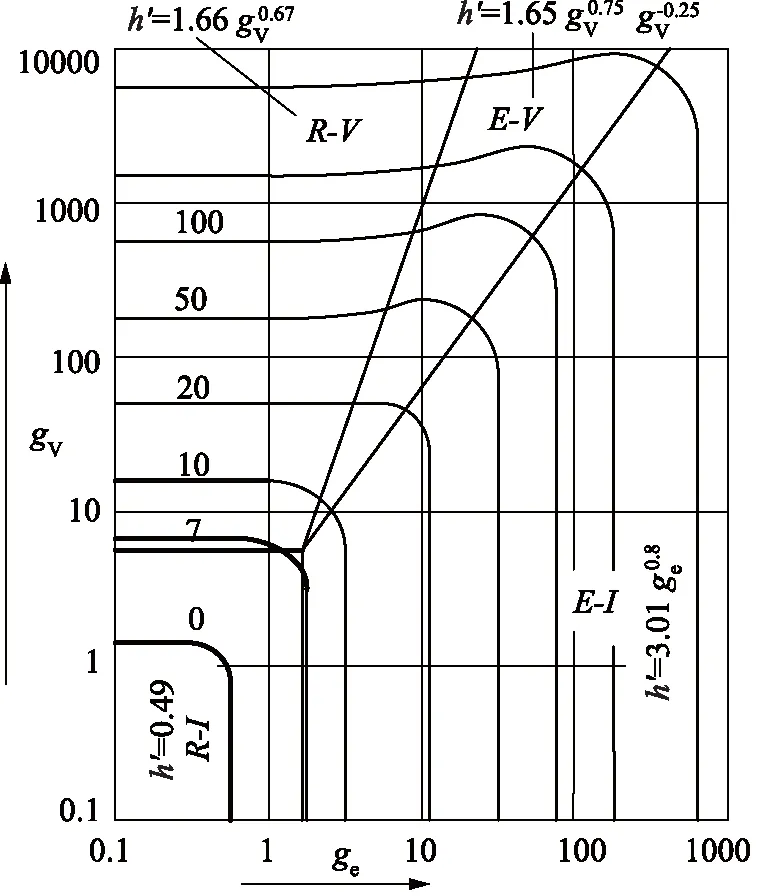
图4 齿面间润滑性质Fig.4 Lubrication properties between tooth flanks
齿面间弹流体油膜的形成与局部受载大小、接触材料的弹性、润滑油的黏压特性和黏温特性相关,弹流油膜的形成能够极大提高齿轮的承载能力和寿命。油膜的建立及处于4种流体动力润滑中的哪种润滑状态主要取决于最小油膜厚度及油膜比厚:
(15)
(16)
(17)
(18)
(19)
式中,h′—— 无量纲最小油膜厚度
hmin—— 最小油膜厚度,m
μ—— 常压下黏度,Pa·s

gV—— 无量纲压黏参数
αp—— 黏压指数,m2/N
R—— 当量曲率半径,m
ge—— 无量纲弹性参数
E—— 当量弹性模量,N2/m
n1—— 主动齿轮转速,r/min
a—— 中心距,m
αn—— 法向压力角,rad
i—— 传动比
λ—— 油膜比厚
σ1,σ2—— 主、从动齿轮表面粗糙度的均方根偏差,m
油膜比厚与不接触时间t的关系如图5所示,当油膜比厚λ小于0.8时为边界润滑状态,齿面将发生磨损,甚至胶合,当λ等于0.8~3时,为混合润滑状态,当λ大于3时,能够保证流体动力润滑的工作条件。一般认为当λ大于1.5~2就能获得接近流体动力润滑的工作条件。
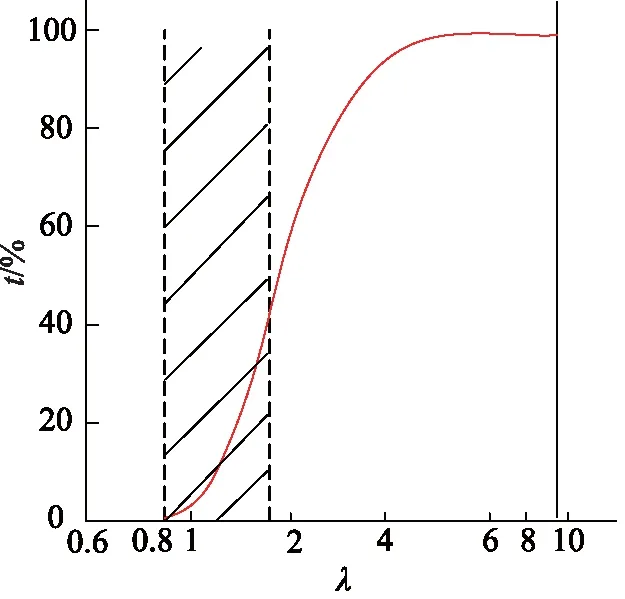
图5 油膜比厚对工作面接触的影响Fig.5 Influence of oil film thickness on working surface contact
齿轮轮齿在一个啮合周期内的油膜厚度如图6所示,油膜厚度s最小值为hmin为0.034 μm,油膜比厚λ为0.056,最大油膜厚度hmax为0.156 μm,油膜比厚λ为0.340,因此可知,螺旋角修形α对油膜厚度和油膜比厚影响甚微,且啮合齿轮处于边界润滑状态。
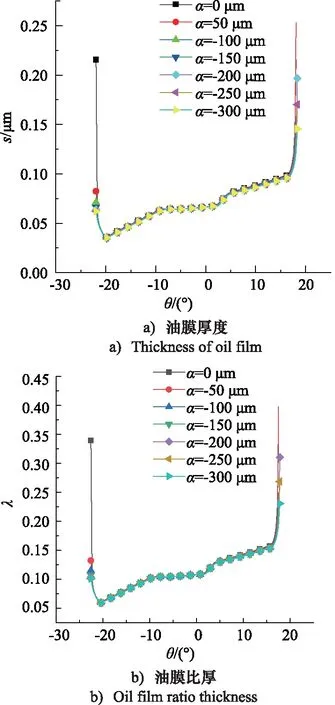
图6 油膜变化Fig.6 Oil film variation
3.2 螺旋线修形量对齿轮传动特性的影响
齿轮渐开线线形处于理想状态,达到绝对刚性的实际齿轮传动中,由于受到制造和安装误差、弹性变形及高速重载等多种因素的影响,传动误差必然存在,传动误差是引起噪声的主要因素,在类似于斜齿轮啮合过程中,对螺旋线修形量进行深入研究。
在啮合齿轮的一个旋转角度(θ)周期内,针对-300~0 μm下的7种螺旋线修形量下的传动误差进行了对比分析,如图7所示,随着螺旋线修形量的增加,传递误差eα不断减小,传递误差范围由-280~-191 μm降至-198~-111 μm,最大传递误差降低82 μm,最低传递误差降低80 μm,传递误差分别降低29%和41%,由此可见,通过螺旋线修形,能够显著降低传递误差,减少噪声的产生。
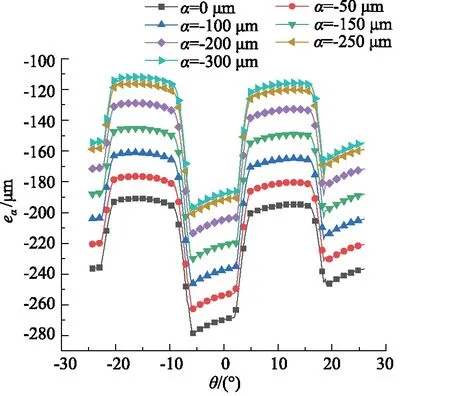
图7 齿轮传递误差Fig.7 Gear transmission error
3.3 螺旋线修形对齿面应力分布的影响
齿面应力分布如图8所示,在齿宽方向上不进行螺旋线修形时,偏载严重,在齿宽方向,载荷分布范围为-3616~-243 N/mm,齿宽两端的应力大小相差-3373 N/mm,随着螺旋线修形量的不断增加,当增加到-300 μm时,在齿宽方向受力主要集中在齿宽中段,且两侧与中段载荷分布相差不大,载荷分布范围为-2194~-1860 N/mm,齿宽两端的应力仅相差-334 N/mm,在整个齿宽方向上应力分布基本达到了比较均匀的程度。
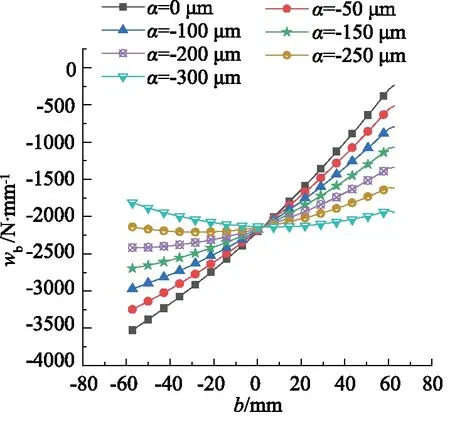
图8 齿面应力分布Fig.8 Stress distribution on tooth surface
如图9所示,螺旋线修形量Mv从0 μm增加至-300 μm,最大线载荷与最小线载荷的差值eF由-3373 N/mm降低至-334 N/mm,降幅达90%,齿宽方向载荷均载程度Eq由6.47%上升到84.78%,增幅达78.31%。由此可见螺旋线修形能够显著改善因传递误差引起的偏载现象。
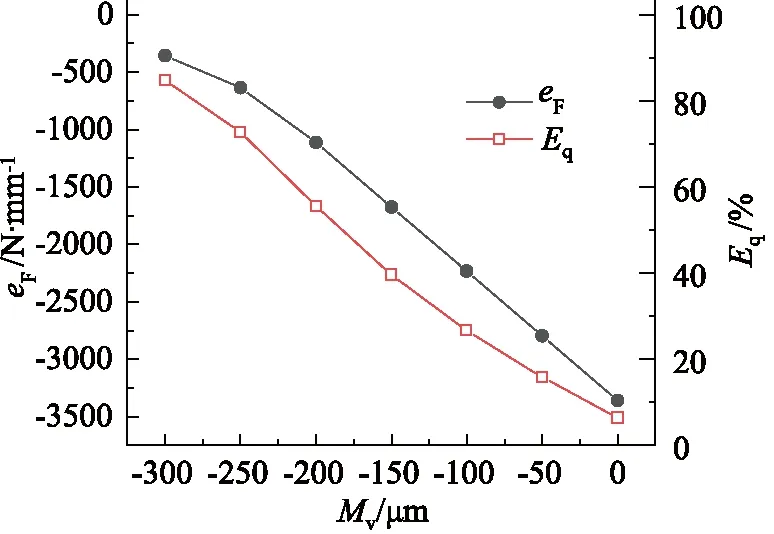
图9 修形量与载荷均载程度的关系Fig.9 Relationship between modification amounts and degree of load equalization
螺旋线修形量α为-50, -100, -150, -200, -250, -300 μm的接触斑点分别如图10a~图10f所示, 螺旋线偏差得到显著修正, 接触斑点呈现向典型的规范靠近[12]。
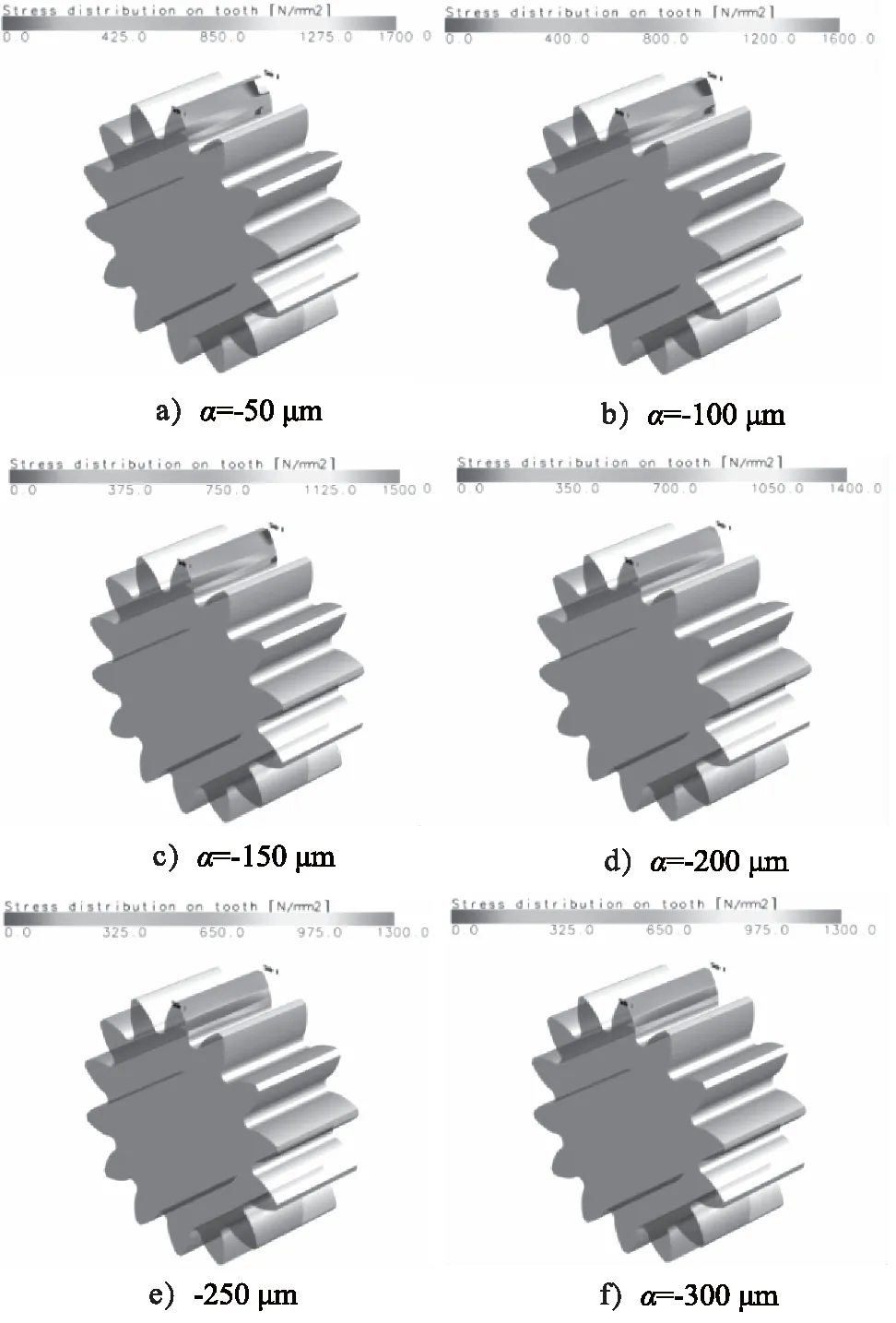
图10 接触斑点图Fig.10 Contact spot map
3.4 螺旋线修形对载荷分布系数的影响
螺旋线载荷分布系数KHβ是考虑沿齿宽方向载荷分布不均匀对齿面接触应力影响的系数,影响其分布的主要因素是轴线平面内的偏差fΣδ和垂直平面内的偏差fΣβ。KHβ值越大则载荷分布越不均,接触应力越集中,KHβ越小则载荷分布越均匀,当KHβ接近于1时,无限接近于均匀分布。轴线平面内的偏差fΣδ和垂直平面内的偏差fΣβ之间的关系见图11。
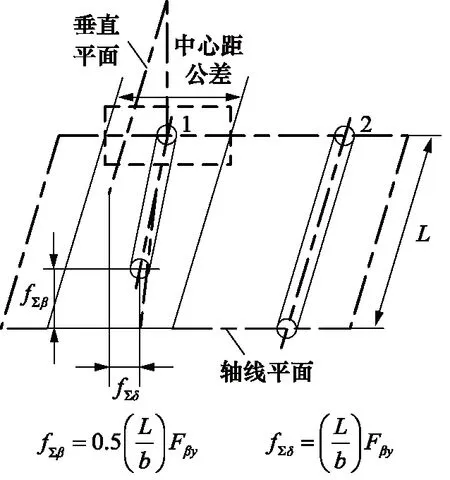
图11 轴线平行度偏差Fig.11 Axis parallelism deviation
由图12可知,随着螺旋线修形量的增加,当修形量由0 μm达到-300 μm时,轴线平面内的偏差fΣδ和垂直平面内的偏差fΣβ随着修形量的增大逐渐减下,螺旋线载荷分布系数KHβ由1.7267降至1.0475,降幅达到39.3%,其值无限接近于最佳值1,数值上仅相差0.0475。
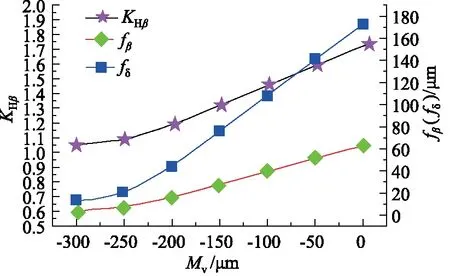
图12 修形量与螺旋线载荷分布系数的关系Fig.12 Relationship between amount of trimming and distribution coefficient of helix load
4 结论
(1) 针对螺旋线修形对润滑油膜、传动误差、齿面应力分布以及载荷分布系数的影响进行了细致的分析。结合KISSsoft软件可以快速获取影响结果,加速产品样机原型迭代过程,缩短研发周期,提升研发质量;
(2) 螺旋线修形对油膜的润滑状态和油膜厚度影响甚微;
(3) 相比未修形的啮合齿轮组,修形使齿轮表面载荷均匀分布程度提高78.31%,传动误差降低41%,螺旋线载荷分布系数降幅达到39.3%。因此,螺旋线修形能够显著改善因各种因素综合引起的螺旋线偏差,改善传动状态,提高传动质量。
