具有负载柔性的液压伺服系统整形滑模控制

王伟平， 杜文芳

(1.江苏师范大学 机电工程学院， 江苏 徐州 221116； 2.中国矿业大学 机电工程学院， 江苏 徐州 221116)

引言

液压伺服系统与气动和电动伺服系统相比具有功率密度大、响应快、精度高等优势，在诸多领域得到越来越广泛的应用，如足式仿生机器人、液压悬架、轧机等[1-3]。

在液压伺服控制系统研究中，往往假设执行器与负载之间的机械连接或传动机构是完全刚性的，而实际上液压执行器在向负载传递扭矩或驱动力时总是存在一定的弹性变形。现有的研究通常忽略结构刚度的影响或仅考虑负载与环境的接触刚度，然而在类似连铸结晶器[4]等大惯量伺服系统以及柔性臂[5]等控制场合，需要考虑结构刚度对控制性能的影响，并且此时负载驱动环节为两自由度系统。当对伺服系统的快速性要求较高时，液压 - 机械的综合谐振频率将限制系统带宽并影响综合系统的控制精度及稳定性。在大型振动台、重型机床等大惯量、大功率伺服系统中均会遇到类似的问题。因此，当考虑负载连接刚度的影响时，半闭环系统的稳定性要比全闭环系统优越[4]。此外，由于半闭环系统的阶数比全闭环系统低，在控制器设计方面更具有优势。针对以上问题，设计了一种半闭环控制策略，即对液压缸活塞杆位移采用闭环控制，而对负载的最终位移采用开环控制。

对于闭环控制部分，首先需要尽量克服超调、振荡等问题对负载振动的进一步激发。液压伺服系统存在时变参数、外部干扰、未建模动态等问题，是一种典型的强非线性系统[6-7]。针对这些问题，国内外学者提出了很多非线性控制策略，如H∞控制[8]、自适应鲁棒控制[9]、输出反馈控制[10]以及基于神经网络或模糊控制的智能控制算法[11-12]。在实际的工业生产中，PID控制作为一种经典的控制方法以其结构简单和可靠性高的特点仍然占据主导地位[13]。然而这种控制方法在跟踪阶跃等误差变化较大的信号时容易出现超调、振荡等问题，且在稳定性分析以及参数整定方面仍然存在一些缺陷。滑模控制(Sliding Mode Control,SMC)作为鲁棒控制的一种，可以使被控状态以柔顺、过阻尼的方式跟踪期望信号。然而当状态轨迹到达滑模面后，由于其难以严格地沿着滑模面向平衡点运动，而是在滑模面两侧来回穿越，从而产生抖振问题。抖振不仅影响控制的精确性、增加能量消耗, 而且系统中的高频未建模动态很容易被激发起来, 破坏系统的性能, 甚至使系统产生振荡或失稳, 损坏控制器部件[14]。基于此，KIKUUWE等[15]提出了一种结合了PID控制和SMC优点的代理滑模控制(Proxy Sliding Mode Control,PSMC)。当跟踪误差较大时，PSMC表现出理想滑模控制的动态特性，避免了采用PID控制时的超调等问题；而当跟踪误差较小时，PSMC表现出PID控制特点，即直接根据跟踪误差调整控制信号从而保证控制精度[16-17]。此外，这种控制方法从理论上取消了不连续的符号函数，因此可以看成是一种连续型控制器，并且与利用双曲正切等函数进行的近似方法具有本质不同[18]。鉴于PSMC的优点，这种方法被应用于诸如气动执行器[19]、压电驱动[20]等领域。然而以上研究的被控对象均为二阶系统，未见应用于三阶液压伺服系统的PSMC控制。此外，传统的PSMC研究缺乏较为完备的稳定性证明且较少考虑大负载扰动情况下的鲁棒性问题，当系统未建模动态及外扰较大时将对控制性能产生较大影响。基于以上考量，本研究将扰动观测器与代理滑模控制结合以提高控制器鲁棒性。同时，为了避免在控制器设计时对测量信号求导而导致噪声放大，在观测器设计以及控制器设计阶段分别采用辅助状态变量和动态面控制方法，从而形成了一种基于扰动观测器的代理滑模控制(Disturbance Observer-based Proxy Sliding Mode Control，DPSMC)，并基于无源性理论及Lyapunov方法给出了稳定性证明。

对于开环控制部分，主要目的是克服负载在连接刚度影响下的振动问题，从而保证最终的控制精度。根据负载驱动部分的特性参数，首先利用零振荡(Zero Vibration，ZV)输入整形器对负载期望轨迹进行修正。然后利用闭环控制部分使液压缸活塞杆的运动位移跟踪修正后的轨迹，从而使活塞杆最终传递到负载的轨迹无振动跟踪期望轨迹。本研究将开环和闭环控制结合，最终形成了一种适用于考虑连接刚度的整形滑模控制(Zero Vibration-Disturbance Observer-based Proxy Sliding Mode Control，ZV-DPSMC)。理论分析及仿真结果表明所提出的控制方法能够在保证稳定性的前提下提高系统抗干扰能力、减小滑模抖振及控制超调并可以使负载无振荡到达期望位置。

1 模型建立

液压缸活塞的力平衡方程可表示为：

(1)

其中，xc=xL-xm。

式中，xL—— 液压缸活塞位移

xm—— 负载位移

mL—— 活塞质量

p1，p2—— 液压缸两腔压力

A1，A2—— 液压缸两腔面积

Bc—— 活塞与负载间的阻尼系数

ks—— 活塞与负载的连接刚度

Fd—— 外扰及未建模动态

液压缸无杆腔流量及有杆腔流量可表示为：

(2)

(3)

式中,Q1，Q2—— 液压缸无杆腔及有杆腔流量

ps—— 系统供油压力

kq，kx—— 阀的控制参数

ρ—— 油液密度

u—— 控制输入信号

忽略泄漏的影响，液压缸两腔的压力动态可表示为：

(4)

式中，Vh1—— 液压缸无杆腔以及连接管路的容积

Vh2—— 液压缸有杆腔以及连接管路的容积

βe—— 有效体积弹性模量

定义液压缸驱动部分的状态变量为：

(5)

联立上述表达式可得系统状态空间方程为：

(6)

式中，d1，d2—— 力平衡方程和压力动态中的不确定性及扰动

其中,

式(6)为控制输入u与液压缸活塞位移xL之间的状态空间方程，而液压缸活塞位移xL与负载位移xm之间的传递函数可表示为：

(7)

式中，m—— 负载质量

为便于控制器设计及分析，作如下合理假设：

(1) 扰动d1和d2可导且导数有界；

(2) 所有状态变量可测；

(3) 活塞与负载连接刚度及阻尼的名义值已知。

一般的液压伺服系统可通过参数辨识方法得到连接刚度，而柔性臂可通过假设模态法和拉格朗日方程得到刚度矩阵。由于柔性臂在一定条件下可以等效为一个弹簧 - 阻尼系统[21]，因此本研究仅讨论一般情况。

2 控制器设计

一方面，由式(6)和式(7)可以看出综合系统的阶数较高，如果直接进行控制器设计将较为困难。另一方面，根据液压弹簧刚度理论可知，液压弹簧刚度和负载连接刚度为串联关系，因此如图1所示的机械液压综合系统的刚度小于两者中任何一个[22]。

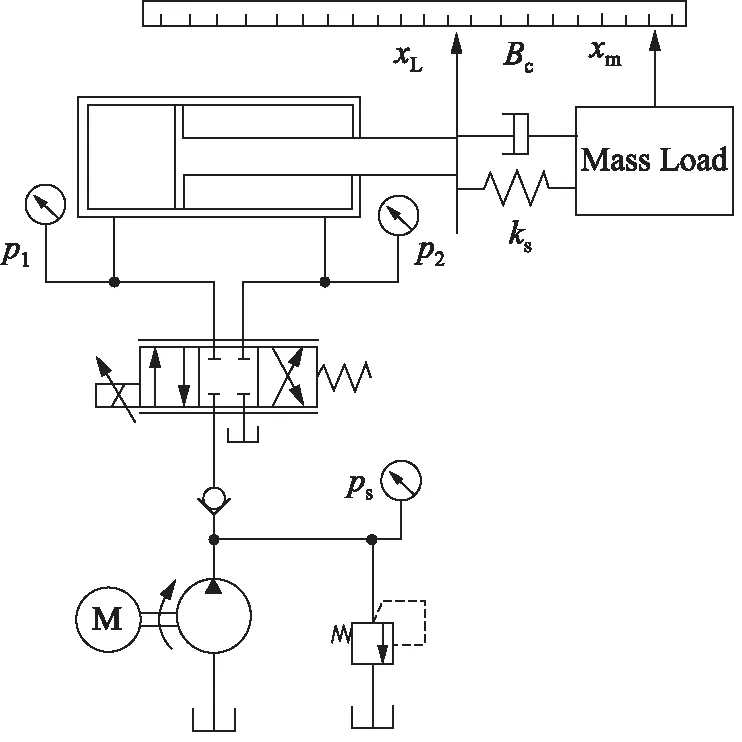
图1 液压伺服系统原理Fig.1 Schematic diagram of hydraulic servo system

以往的液压伺服系统中往往认为负载连接刚度大于液压弹簧刚度，因此液压系统的固有频率就决定了综合系统的特性。而当负载连接刚度接近甚至小于液压弹簧刚度时，负载连接刚度将严重制约系统响应及稳定性。基于以上分析， 本研究仅对液压缸活塞杆位移进行闭环控制，而活塞杆对负载的驱动部分采用开环控制。由式(7)可知负载驱动部分的传递函数中包含二阶振荡环节。因此当阻尼较小时，由活塞杆通过弹簧阻尼系统驱动负载将导致负载的振动。因此，本研究首先由式(7)得到固有频率及阻尼比，并根据ZV输入整形原理设计理想的活塞杆位移以期实现无振动驱动，然后利用闭环控制实现活塞杆位移的精确跟踪。根据上述原理可以得到控制器设计框图，如图2所示。

图2 控制器整体框图Fig.2 Overall block diagram of controller

2.1 扰动观测器

设计高增益扰动观测器为:

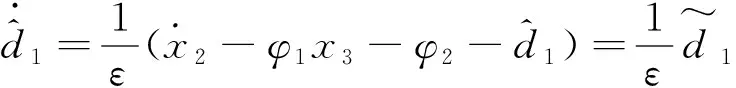
(8)

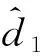
(9)

扰动估计误差的动态为：

(10)

2.2 代理滑模控制

将式(6)中前两阶状态方程改写为：

(11)

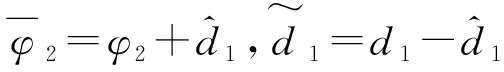
针对式(11)，定义滑模面如下[18]：

(12)

式中，xd—— 活塞杆的期望的位置

xp—— 代理的位置

k1—— 控制增益，大于0

设计基于滑模的代理控制器为：

(13)

其中，mp为代理质量，kp和kd表示PD控制中的比例和微分增益，k2>0为控制增益。

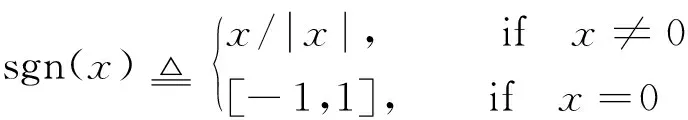
虚拟耦合定义为：

(14)

代理的力平衡方程可表示为：

(15)

由于代理连杆实际上并不存在，因此可以认为代理质量为0，因此有：

uc=up=x3d

(16)

其中，x3d为前两阶系统的虚拟输入。

基于式(15)可得：

(17)

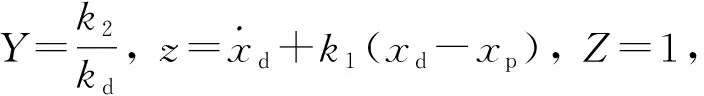
根据符号函数定义且由于Z和Y均大于0，式(17)中的符号函数可改写为：

(18)

将式(18)代入式(17)可得：

(19)

基于文献[15]中式(4)关于符号函数sgn和单位饱和函数sat关系的推理，式(19)可改写成：

(20)

其中，sat(x)x/max(1，|x|)为单位饱和函数，

由上式可进一步根据式(14)及式(16)得到x3d。从式(20)可以看出,代理滑模控制本质上不含有非连续的符号函数,在一定程度上可以看成是一个连续型控制器，从而可以避免滑模抖振问题。此外，基于扰动观测器的代理滑模控制在很大程度上抑制了大负载扰动对控制效果的影响。

由χ的表达式可知通过合理地配置控制增益可以避免χ进入饱和区，从而式(20)可以改写成：

(21)

一种特殊配置为kp=k1kd，此时χ=sL/Y。由于sL有界，当|sL|≤Y时，χ一直在饱和函数的线性区内变化。

定义Lyapunov函数为：

Vp=V1+V2+V3

(22)

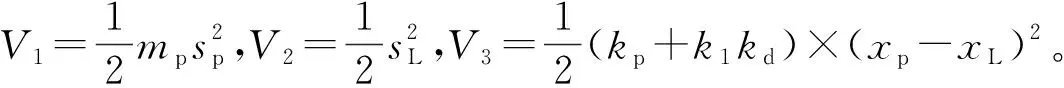
对Lyapunov函数求导可得：

(23)

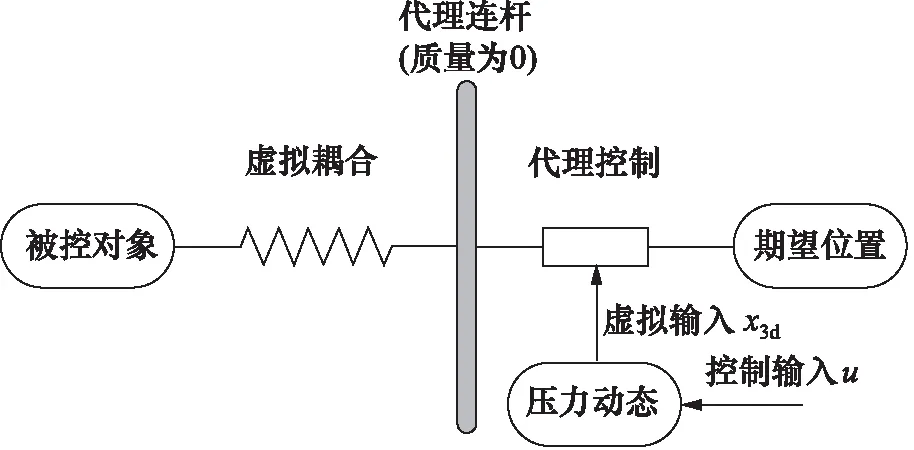
图3 代理滑模控制器基本原理Fig.3 Basic principle of proxy sliding mode controller

2.3 动态面控制

从以上分析可知下一步应通过设计实际控制信号使x3跟踪x3d。虽然由式(14)、式(16)及式(21)可知x3d可以通过合理设置控制器参数从而取消饱和函数并转换为连续可导形式，但为了从理论上避免对x3d求导并减小微分对测量噪声的放大作用，采用动态面方法定义虚拟输入α为x3d的低通滤波器输出[24]，即：

(24)

其中，τ为滤波器时间常数。

定义e=x3-α为输入误差并基于式(6)可得误差动态为：

(25)

根据式(25)可设计控制信号为：

(26)

将式(26)代入式(25)可得：

(27)

定义Lyapunov函数为：

V=Ve+Vp

(28)

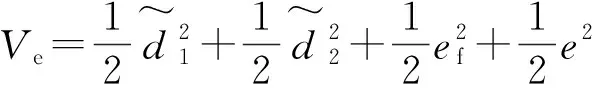
基于式(23)～式(28)对Ve求导可得：

(29)

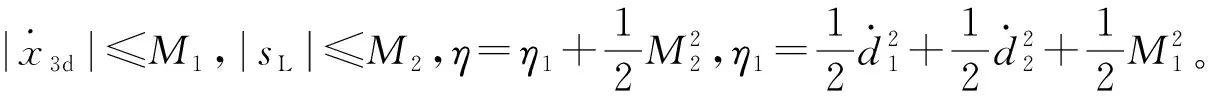
结合式(23)和式(29)可得V的动态为：

k1kp(xp-xL)2+η

(30)

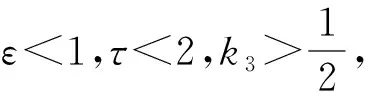
(31)

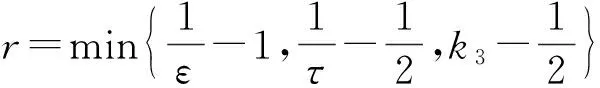
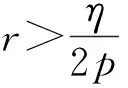
2.4 ZV输入整形控制

输入整形控制时将初始指令与特定的脉冲序列进行卷积，生成的整形指令作为控制系统运动的输入信号[25]。一种包含两脉冲的ZV输入整形器可以表示为：

y=λ1e-t1s+λ2e-t2s

(32)

式中，λ1，λ2—— 脉冲幅值

t1，t2—— 脉冲对应的时滞

参数可具体表示为：

(33)

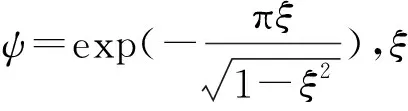
对于本研究中的负载驱动部分而言，固有频率和阻尼比可表示为：

(34)

将具体参数带入上述表达式即可得到ZV输入整形器。

3 仿真研究

为验证本研究所提出方法在液压伺服系统中的有效性及可行性，下面进行对比仿真研究。 选取的液压伺服系统参数如表 1 所示。控制器参数设计为ε=0.001，kp=2500，kd=50，k1=50，k2=1000，k3=1000，τ=0.001。

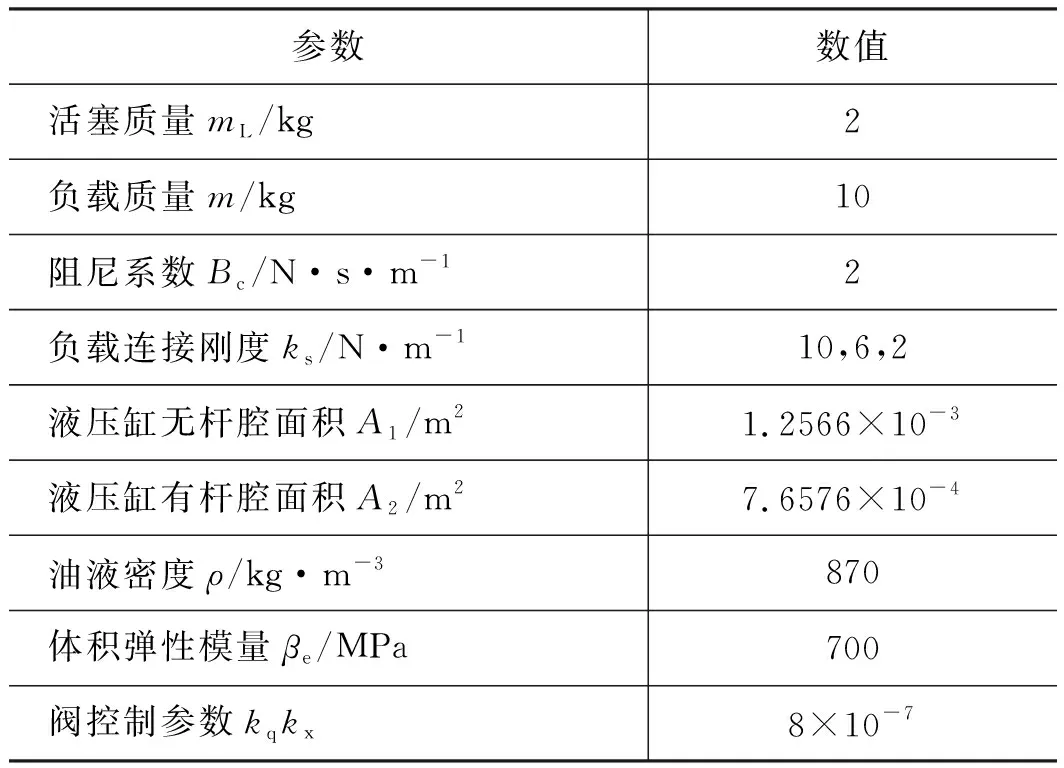
表1 液压系统参数Tab.1 Parameters of hydraulic system

首先验证闭环控制部分的有效性，考察液压缸活塞杆位移的跟踪效果。考虑参考信号为xd=sin(2πt)，为对比分析算法的效果，本研究将PSMC，SMC和PID控制应用于原液压系统，PSMC和DPSMC的控制参数相同。SMC结合反步控制和滑模控制方法，其控制参数为k1=k2=k3=300。PID控制器参数采用试错法确定为kp=20，ki=10，kd=0。从图4可以看出DPSMC，PSMC，SMC在控制效果上优于PID控制，最大跟踪误差分别为1.2，2.5，4.0，12.0 mm。此外，由于与PSMC相比，DPSMC由于具有扰动观测及补偿功能(如图6所示)，因此从图5的跟踪误差曲线中可以看出DPSMC的跟踪误差低于PSMC。

图4 正弦信号下活塞杆位移跟踪效果Fig.4 Tracking performance of cylinder rod under sinusoidal signal

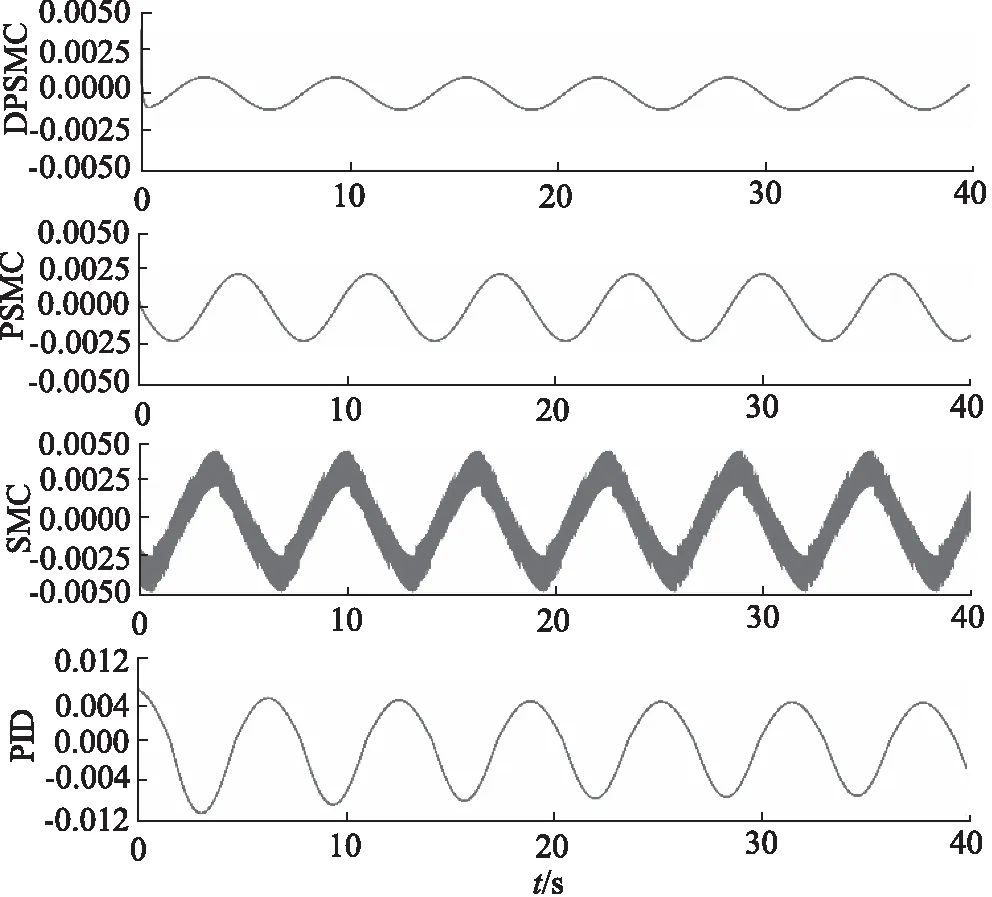
图5 正弦信号下活塞杆位移跟踪误差对比Fig.5 Comparison of tracking errors under sinusoidal signal

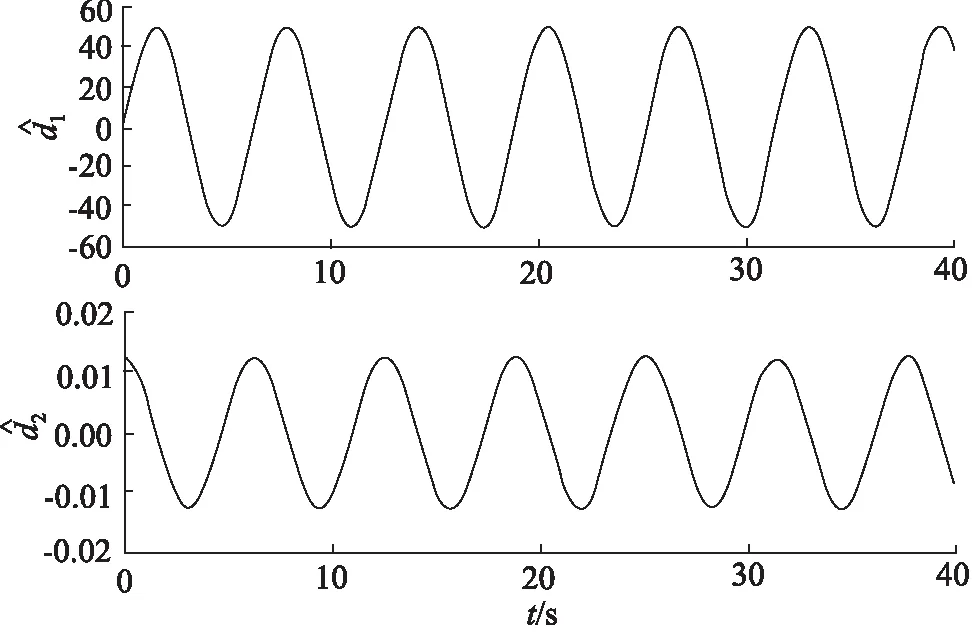
图6 扰动观测结果Fig.6 Observation result of disturbance

图7为DPSMC和SMC控制输入信号的对比。从图中可以看出，所提出的DPSMC整体性能优于其他几种控制方法，可以利用较为连续的控制信号实现高精度跟踪。SMC由于具有不连续的符号函数，因此如要保证较好的跟踪精度将会产生较强的抖振。由于PID控制、PSMC的输出信号均具有连续性，因此本研究仅对比SMC和DPSMC的控制信号。图8为几种方法在不同统计指标下的性能分析，其中最大值、最小值、平均值分别为6.4×10-4，1.4×10-3，2×10-3，4.6×10-3；标准差分别为3.3×10-4，6.8×10-4，1.2×10-3，2.6×10-3其公式如式(35)：

(35)

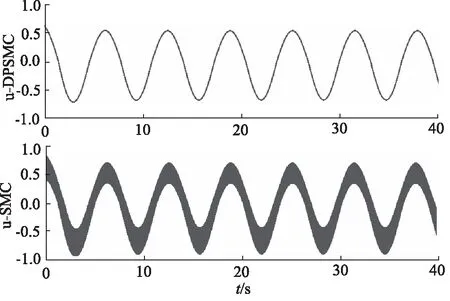
图7 输入信号对比Fig.7 Comparison of input signals

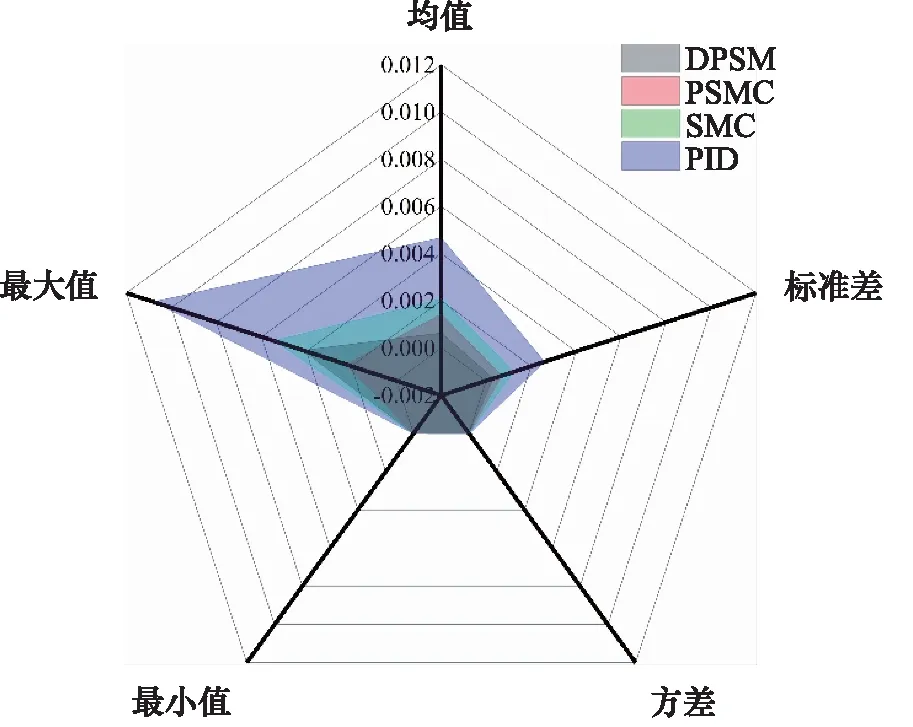
图8 正弦信号控制效果对比Fig.8 Comparison of control performance under sinusoidal signal

为进一步验证所提出算法的有效性，以方波信号为活塞杆位移期望信号进行仿真分析。从图9中可以看出，为了实现较高的跟踪精度，PID控制采用的相对较高的控制增益将会产生超调及振荡等问题。结合图10和图11可以看出， 几种控制方法在最大误差及最小误差方面接近。在平均误差方面，所提出的DPSMC方法优于其他几种方法，均值分别为0.029，0.033，0.047，0.1。

图9 方波信号下活塞杆位移跟踪效果Fig.9 Tracking performance of cylinder rod under square signal

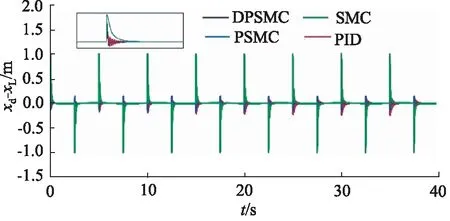
图10 方波信号下活塞杆位移跟踪误差对比Fig.10 Comparison of tracking errors under square signal

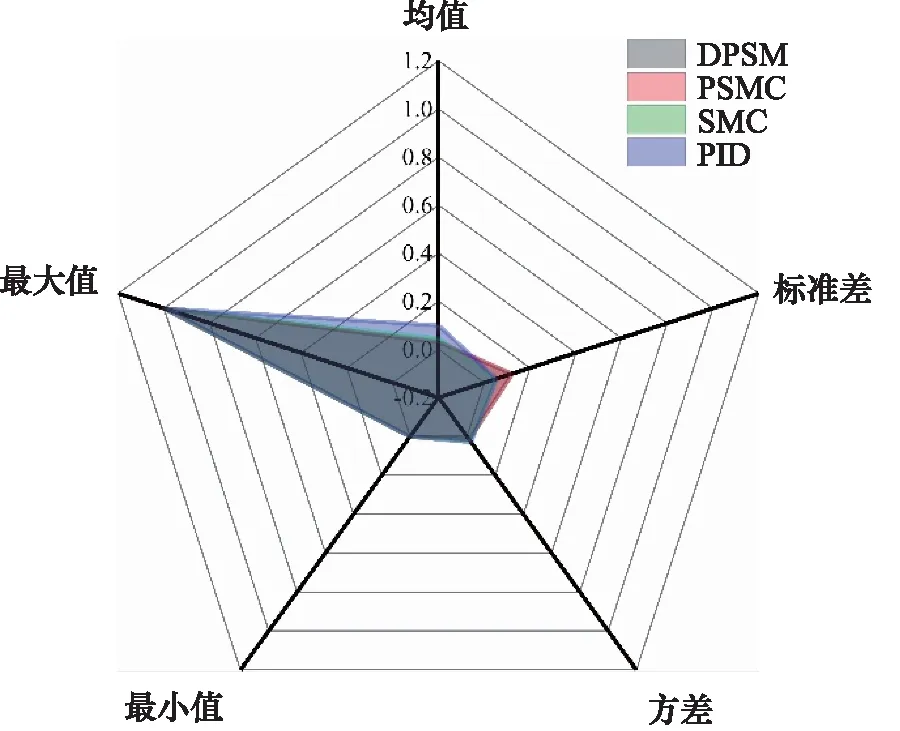
图11 方波信号控制效果对比Fig.11 Comparison of control performance under square signal

从上述仿真结果可以看出所提出的闭环控制方法具有较好的跟踪效果。如果不考虑负载驱动环节的连接刚度问题进行仿真分析(以阶跃响应为例，即以阶跃信号作为xd)，可以得到图12所示的负载位移曲线(分别采用不同的连接刚度值)。从图中可以看出，即使能够对活塞杆位移进行精确控制，但负载的最终位移曲线仍然具有较为严重的振荡。与液压缸行程相比，最大振荡幅值在不同参数条件下分别为125%，100%，75%。

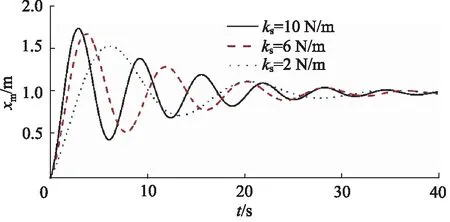
图12 DPSMC条件下负载位移曲线Fig.12 Load displacement curve under DPSMC

图13为利用ZV输入整形方法对阶跃信号进行修正之后的负载位移仿真曲线。从图中可以看出，所提出的ZV-DPSMC可以在抑制负载振荡的前提下实现位移的精确控制。另一方面，从图13可以看出，当负载连接刚度较大时， 由ZV输入整形而产生的时滞较小且超调量也较小。

图13 ZV-DPSMC条件下负载位移曲线Fig. 13 Load displacement curve under ZV-DPSMC

4 结论

针对一类负载连接刚度较低的液压伺服系统，本研究提出了一种结合ZV输入整形器和代理滑模控制的半闭环控制策略ZV-DPSMC。在闭环控制部分，针对PID控制存在的超调问题以及传统基于符号函数的滑模控制所存在的抖振问题，本研究在考虑外扰对控制性能影响的基础上提出了一种基于扰动观测器的代理滑模控制。这种方法一方面可以保留代理滑模控制的优点，另一方面提升了其抗干扰能力。鉴于传统的代理滑模控制通常面向二阶系统，本研究进一步结合动态面控制并将该方法应用于三阶液压伺服系统。在以上研究的基础上获得了一种连续、抗干扰、无抖振控制器。通过无源性理论及李雅普诺夫理论给出了完整的稳定性证明；在开环控制部分，本研究利用ZV输入整形器对期望负载位移进行修正从而实现了负载无振荡定位。通过理论及仿真分析验证了所提出方法的有效性。此外，本研究所提出的方法可以进一步研究以应用于液压驱动柔性臂等需要考虑结构柔性的控制场合。